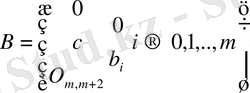Шектеулі облыстағы гиперболалық типті дифференциалдық операторлардың өз-өзіне түйіндестігі және шеттік есептердің шешімдерінің бар болуы, жалғыздығы және дифференциалдық қасиеттері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 64 бет
Таңдаулыға:
КІРІСПЕ
Тақырыптың өзектілігі. Бұл диссертациялық жұмыс шектеулі облыста гиперболалық түрдегі дифференциалдық теңдеудің шешімдерінің бар болуы, жалғыздығы және шешімдерінің дифференциалдық қасиеттерін, сонымен қатар гиперболалық операторлардың бір класының өз-өзіне түйіндестігін зерттеуге арналған.
Гиперболалық теңдеулер үшін шеттік есепті зерттеудің өзектілігі есептегі әртүрлі мәселелерге қойылатын қосымшаның маңыздылығымен тығыз байланыста қолданылатын практика негізінде анықталады және физика, химия, биология, радиофизика және электротехниканың есептерін шешуде қолданылады.
Физикалық есептің шешімінің ерекшелігін шешу негізінде пайдаланылған екінші ретті теңдеудің гиперболалық түрдегі дербес туындылы дифференциалдық теңдеулер теориясындағы алатын орыны зор. Гиперболадық түрдегі теңдеулерді зерттеудің негізі болып XVIII ғасырда зерттелген шектің тербеліс теңдеулері болып табылады. Бұл теңдеулерді зерттеу Г. Галилей, М. Мерцен, Р. Декарт, Х. Гюйгенс, Б. Тейлор, Ж-Л. Даламбер, Л. Эйлер, Д. Бернулли, Ж-Л. Лагранж, П. -С. Лапластың аттарымен байланысты.
Гиперболалык теңдеудің жалпы теориясының койылуы және оның жеке нәтижесін жүйелеу Ж. Б. Фурье, О. -Л. Коши, С. В. Ковалевская, Г. Дарбу, Э. Гурс, Б. Риман, П. -Г. -Л. Дирихле, Ж. Адамар және т. б. ғалымдардың енбектерінен басталған.
Бұл классикалық зерттеулер гиперболалық теңдеулер облысының жаңа әдістерін зерттеулеріне айтарлықтай әсер етті. Сызықты жэне сызықты емес гиперболалық теңдеулер және екінші ретті жүйелер Р. Курсант, К. Фидрихс, Г. Левитан, И. Шаудер, С. Л. Соболев, И. Г. Петровский, Ж. Лере, Л. Гординг, О. А. Ладыженский, Т. Ш. Кальменов және т. б. ізденушілердің жұмыстарында айтарлықтай зерттелген. Ал, О. А. Олейник, Б. Л. Рожденственский, Н. Н. Яненко және т. б. ғалымдардың жұмыстары гиперболалык түрдегі екінші ретті жүйе мен теңдеулерге арналған.
Сингулярлы дифференциалдық теңдеулерді жете зерттеуді кванттық механикада қажет ететіндігі белгілі. Мысалы: шектеусіз облыста берілген теңдеулер. Шектеусіз облыстағы коэффициенттері шектеулі гиперболалық түрдегі теңдеулердің шешімдерінің бар болуы және оның қасиеттері П. Д. Лакс, К. Фидрихс, М. Нагумо, А. М. Нахушев, Т. И. Кигурадзе, Д. С. Джумабаев, А. Т. Асановалардың жұмыстарында толығымен зерттелген.
Мысалы П. Д. Лакс, К. Фридрихс, М. Ногумоның зерттеулерінде

кеңістігінде жатқан
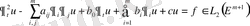
гиперболалық түрдегі екінші ретті дербес туындылы дифференциалдық теңдеудің жалпы шешімдерінің бар болуы
1)
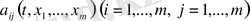 және оның бірінші ретті туындысы үзіліссіз және шектеулі, ал
және оның бірінші ретті туындысы үзіліссіз және шектеулі, ал
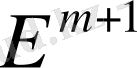 кеңістігінде жатқан
кеңістігінде жатқан
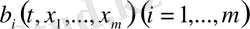 функциясы үзіліссіз және шектеулі функция;
функциясы үзіліссіз және шектеулі функция;
- ,
мұндағы,
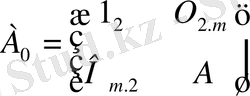 ,
,
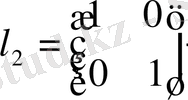 ,
,
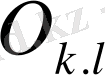 -матрицасының реті
-матрицасының реті
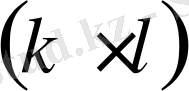 тек қана нөлдік элементтерден тұрады,
тек қана нөлдік элементтерден тұрады,
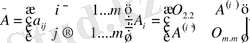 - симметриялы,
- симметриялы,
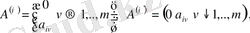
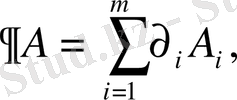
шарттар негізінде дәлелденген.
Жұмыс мақсаты. Гиперболалық операторлардың бір класының өз-өзіне түйіндестігін көрсету.
Зерттеу әдістемесі. Зерттеу барысында М. Өтелбаевтың жұмыстарында пайдаланған локализация әдісі, априорлық бағдар әдісі, Фурье түрлендірулері, сонымен қатар функционалдық анализдің кейбір қолданылуларында пайдаланған әдістер қолданылады.
Ғылыми жаңашылдығы. Гиперболалық түрдегі дифференциалдық операторлардың бір класы үшін өз-өзіне түйіндестігін зерттеуге арналған.
Жұмыста төмендегідей жаңа нәтижелер алынды:
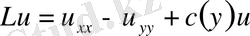
операторы
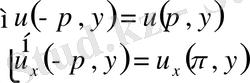
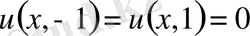
шеттік шарттар негізінде
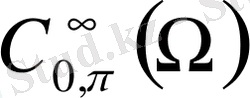 - шексіз дифференциалданатын кеңістігінде қарастырылған. Мұндағы,
- шексіз дифференциалданатын кеңістігінде қарастырылған. Мұндағы,
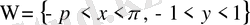 - ашық тік төртбұрыш.
- ашық тік төртбұрыш.
Оператордың өз-өзіне түйіндестігін зерттеу барысында төмендегі шарттар толығымен дәлелденді:
1)
 операторының симметриялы екендігі;
операторының симметриялы екендігі;
2)
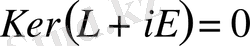 , яғни
, яғни
 операторының ядросы бос екендігі;
операторының ядросы бос екендігі;
3)
 операторының кері
операторының кері
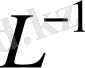 кері операторы бар және ол шектеулі болатындығы;
кері операторы бар және ол шектеулі болатындығы;
4)
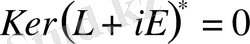 , яғни
, яғни
 операторына түйіндес
операторына түйіндес
 операторының ядросы бос екендігі;
операторының ядросы бос екендігі;
5) (2) -(3) шеттік шарттар негізінде зерттелген
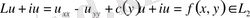
есебінің
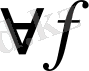 үшін жалғыз ғана шешімі бар екендігі.
үшін жалғыз ғана шешімі бар екендігі.
Теориялық және практикалық маңыздылығы. Жұмыс теориялық сипатта жасалған, ол жоғары курс студенттеріне арнайы курс оқу барысында қолданылатын теориялық қызығушылық тудыратын нәтижелер алынды.
Диссертация құрылымы. Диссертация кіріспеден, үш бөлімнен, қорытындыдан және қолданылған әдебиеттер тізімінен тұрады.
Бірінші бөлімде әдебиетке шолу жасалып, анализдің кейбір фактілері мен тұжырымдары келтірілген және олар мысалдармен ұштастырылған.
Екінші бөлімде ішектің тербелісінің теңдеуін қорытып шығару, Даламбер формуласы, Фурье әдісі, мембрана тербелісінің теңдеуін қорыту қарастырылған.
Үшінші бөлімде гиперболалық түрдегі дифференциалдық операторлардың бір класының өз-өзіне түйіндестігін зерттеуге арналған.
Функционалдық анализдің негізгі түсініктері
1. 1. Метрикалық кеңістік ұғымы
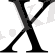 - кез келген жиын болсын. Оның элементтерін
- кез келген жиын болсын. Оның элементтерін
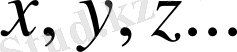 әріптерімен белгілейміз.
әріптерімен белгілейміз.
Екі айнымалылы, нақты сан мәнді
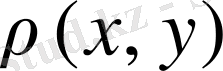 функциясы
функциясы
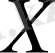 жиынының элементтерінде анықтап және мына төмендегі шарттарды қанағаттандыратын болсын:
жиынының элементтерінде анықтап және мына төмендегі шарттарды қанағаттандыратын болсын:
- (симметриялық шарты )
- жәнетеңдігі тек қанаболғанда орындалады (тепе-теңдік шарты)
- Кез келгенэлементтері үшін:
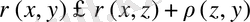 (1. 1. 1)
(1. 1. 1)
теңсіздігі орындалады. (Бұл теңсіздік үшбұрыш теңсіздігі деп аталады) .
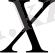 -жиынында анықталған, осы қасиеттерге ие
-жиынында анықталған, осы қасиеттерге ие
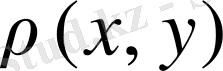 функциясы арақашықтық немесе метрика деп аталады. Метрика үшін қойылған үш шарт метрика аксиомалары деп аталады.
функциясы арақашықтық немесе метрика деп аталады. Метрика үшін қойылған үш шарт метрика аксиомалары деп аталады.
Анықтама.
Метрика анықталған
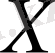 жиынын метрикалық кеңістік деп атайды.
жиынын метрикалық кеңістік деп атайды.
Метрикалық кеңістік
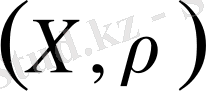 түрінде белгіленеді, бірақ көбінесе қысқаша, тек жиынның ғана таңбасын көрсетіп,
түрінде белгіленеді, бірақ көбінесе қысқаша, тек жиынның ғана таңбасын көрсетіп,
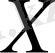 арқылы белгілейміз.
арқылы белгілейміз.
Метрикалық кеңістікте жатқан кез келген
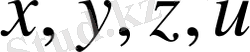 нүктелері үшін үшбұрыш теңсіздігін қайталай қолданып, мына теңсіздіктерді жазайық:
нүктелері үшін үшбұрыш теңсіздігін қайталай қолданып, мына теңсіздіктерді жазайық:
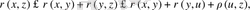
яғни
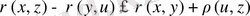 (*)
(*)
Осыған ұқсас,

яғни
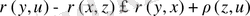 (**)
(**)
Енді (*), (**) теңсіздіктері
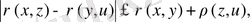 (1. 1. 1
/
)
(1. 1. 1
/
)
теңсіздігіне пара-пар. Бұны төртбұрыш теңсіздігі деп аталады. Осы теңсіздіктен
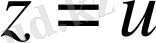 болған жағдайда
болған жағдайда
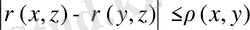 , (1. 1. 1
//
)
, (1. 1. 1
//
)
теңсіздігі шығады, ал бұл-екінші үшбұрыш теңсіздігі.
Тұжырым.
 -кез келген нормаланған сызықтық кеңістік болсын.
-кез келген нормаланған сызықтық кеңістік болсын.
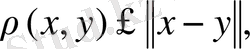 (1. 1. 2)
(1. 1. 2)
теңдігі осы кеңістікте метриканы анықтайды.
Дәлелдеуі.
Шарт бойынша
 -нормаланған сызықтық кеңістік. Метриканың бірінші аксиомасы орындалатын (1. 1. 2) кеңістігінен белгілі. Сондай-ақ,
-нормаланған сызықтық кеңістік. Метриканың бірінші аксиомасы орындалатын (1. 1. 2) кеңістігінен белгілі. Сондай-ақ,
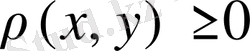 екендігі де нормаға сәйкес қасиеттен шығады. Егер
екендігі де нормаға сәйкес қасиеттен шығады. Егер
 болса, онда
болса, онда
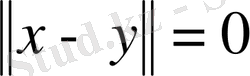 , демек, норманың қасиеті бойынша,
, демек, норманың қасиеті бойынша,
 , яғни
, яғни
 .
.
Енді метриканың үшінші аксиомасын, яғни (1. 1. 1) теңсіздігін дәлелдейік. Кеңістіктің кез-келген
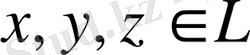 элементтерін алып, норманың үшінші аксиомасын пайдаланып, метрика үшін үшінші аксиоманың орындатынын көреміз:
элементтерін алып, норманың үшінші аксиомасын пайдаланып, метрика үшін үшінші аксиоманың орындатынын көреміз:
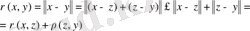 (1. 1. 3)
(1. 1. 3)
(1. 1. 2) теңдігінің норманы анықтайтыны, сонымен бірге
 жиыны метрикалы жиын, яғни метрикалық кеңістік болғаны дәлелденді.
жиыны метрикалы жиын, яғни метрикалық кеңістік болғаны дәлелденді.
Метрикалық кеңістіктерге мысалдар
1
0
.
 (
n
өлшемді кеңістік) болсын. Егер
(
n
өлшемді кеңістік) болсын. Егер
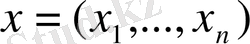 және
және
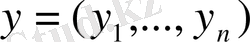 бұл кеңістіктің кез келген екі нүктесі болса, онда
бұл кеңістіктің кез келген екі нүктесі болса, онда
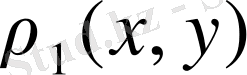 метрикасын мына өрнекпен
метрикасын мына өрнекпен
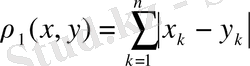
анықтауға болады, себебі
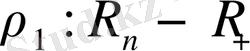 жоғарыдағы шарттарын қанағаттандырады. Олай болса,
жоғарыдағы шарттарын қанағаттандырады. Олай болса,
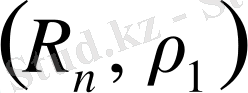 -метрикалық кеңістік.
-метрикалық кеңістік.
2
0
. Егер
x
пен
y
нүктелері берілген болса, онда
 ара қашықтығын
ара қашықтығын
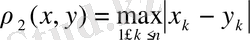
өрнегі бойынша да анықтауға болады. Бұл өрнектің де 1) -3) шарттарын қанағаттандыратындығы көреміз. Олай болса,
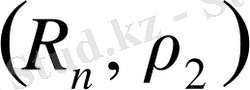 -метрикалық кеңістік.
-метрикалық кеңістік.
3
0
.
 -нақты сандар жиыны болсын,
x
пен
y
нүктелерінің ара қашықтығын
-нақты сандар жиыны болсын,
x
пен
y
нүктелерінің ара қашықтығын
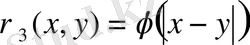 өрнегі бойынша анықтауға болады. Мұндағы
φ(α)
барлық
α≥0
үшін анықталған, екі рет үзіліссіз дифференциалданатын, монотонды өспелі (
φ
/
(α) >0, φ
//
(α) <0)
және
φ(0) =0
болатын функция. Бастапқа 1), 2) қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
φ(α+β) ≤ φ(α) +φ(β)
қатынасынан шығады. Сондықтан
өрнегі бойынша анықтауға болады. Мұндағы
φ(α)
барлық
α≥0
үшін анықталған, екі рет үзіліссіз дифференциалданатын, монотонды өспелі (
φ
/
(α) >0, φ
//
(α) <0)
және
φ(0) =0
болатын функция. Бастапқа 1), 2) қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
φ(α+β) ≤ φ(α) +φ(β)
қатынасынан шығады. Сондықтан
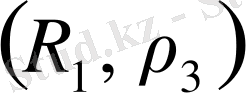 -метрикалық кеңістік. Егер
-метрикалық кеңістік. Егер
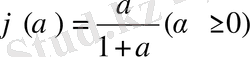 деп алсақ, онда
деп алсақ, онда
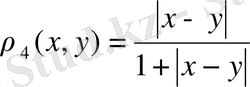
өрнегі де 1) -3) шарттарын қанағаттандырады. Олай болса,
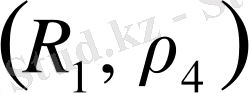 - метрикалық кеңістік. Бұл жағдайда
- метрикалық кеңістік. Бұл жағдайда
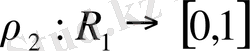
4
0
. Компекс сандар жазықтығындағы радиусы бірге тең ашық дөңгелектің
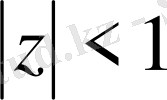 екі нүктесі-
екі нүктесі-
 мен
мен
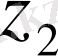 нүктелерінің ара қашықтығын
нүктелерінің ара қашықтығын
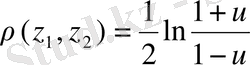
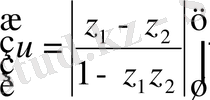
өрнегімен анықтауға болады. Метрикалық кеңістіктің аксиомалары орындалуы себепті бұл метрикалық кеңістік.
Бастапқы үш мысалдағы кеңістіктер векторлық (сызықтық) кеңістіктер болса, соңғы мысалдағы кеңістік сызықты емес метрикалық кеңістік.
5 0 . х=l 1 ; бұл жиынның нүктелері x=(x 1 , . . . , х n , . . . )
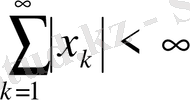
шарттарын қанағаттандыратын (яғни абсолют жинақталатын қатарлар ) сан тізбектері. Егер
у
 l
1
(мұндағы
у=(у
1
, . . . , у
n
, . . . )
) болса, онда метриканы
l
1
(мұндағы
у=(у
1
, . . . , у
n
, . . . )
) болса, онда метриканы
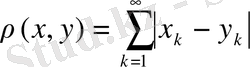
өрнегімен анықтауға болады. Бұл жағдайда да бастапқы екі қасиет оңай тексеріледі, ал үшіншісін былай тексеруге болады.
Егер
x=(x
1
, . . . , х
n
, . . . )
және
у=(у
1
, . . . , у
n
, . . . )
,
z
 l
1
болса, онда кез келген
n
үшін
l
1
болса, онда кез келген
n
үшін
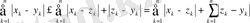
теңсіздігінен шекке көшу арқылы
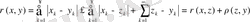
теңсіздігін алуға болады. Олай болса,
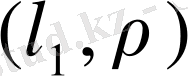 -метрикалық кеңістік. Кейде бұл кеңістікті
-метрикалық кеңістік. Кейде бұл кеңістікті
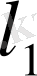 арқылы ғана белгілейміз.
арқылы ғана белгілейміз.
- Сызықты және нормаланған кеңістіктер
Анықтама.
Егер қайсыбір
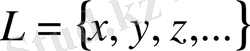 жиынында:
жиынында:
- Кез келгенэлементтері үшін олардың қосындысы деп аталатынэлементі анықталған болса және бұл екі элементті қосу амалы үшін мына қасиеттер орындалса:(қосудың коммутативтік қасиеті) ; ( қосудың ассоциативтік қасиеті) ; Кез келгенүшінтеңдігі орындалатын бір ғана
 элементі бар болуы (нөлдік элемент) ;
элементі бар болуы (нөлдік элемент) ;
- Кез келгенүшінтеңдігі орындалатынэлементі (ке қарама-қарсы элемент) бар және ол әрүшін біреу ғана болса;
- Кез келгенжәне кез келгеннақты (немесе комлекс) саны үшінэлементі менсанының көбейтіндісі деп аталатынэлементі анықталған болса және бұл элементті санға көбейту амалы мен элементтерді қосу амалдары мына төмендегі шарттарды қанағаттандыратын болса. -скалярлар;
онда бұл
 жиыны сызықтық кеңістік деп аталады.
жиыны сызықтық кеңістік деп аталады.
 жиынының элементтерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады.
жиынының элементтерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады.
 жиынының элементтері көбейтілетін сандар жиыны ретінде нақты сандар жиыны
жиынының элементтері көбейтілетін сандар жиыны ретінде нақты сандар жиыны
 немесе комплекс сандар жиыны
немесе комплекс сандар жиыны
 алынуына қарай нақты сызықтық кеңістік немесе комплекс сызықтық кеңістік пайда болады.
алынуына қарай нақты сызықтық кеңістік немесе комплекс сызықтық кеңістік пайда болады.
Егер
 жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалады. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар орындалады.
жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалады. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар орындалады.
Сызықтық кеңістікке мысал:
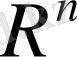 арқылы
арқылы
 өлшемді координаттық кеңістік белгіленеді. Бұл кеңістікте
өлшемді координаттық кеңістік белгіленеді. Бұл кеңістікте
 жиыны
жиыны
 өлшемді
өлшемді
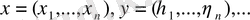 векторлары алынады. Мұндағы
векторлары алынады. Мұндағы
 , сондай-ақ,
, сондай-ақ,
 -кез келген нақты (немесе комплекс) сандар-вектордың координаттары. Екі вектордың қосындысы
-кез келген нақты (немесе комплекс) сандар-вектордың координаттары. Екі вектордың қосындысы
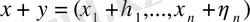 түрінде, яғни берілген векторлардың аттас координаттарын қосу нәтижесінде пайда болған вектор ретінде анықталады, ал
түрінде, яғни берілген векторлардың аттас координаттарын қосу нәтижесінде пайда болған вектор ретінде анықталады, ал
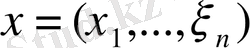 вектордың
вектордың
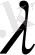 санының көбейтіндісі
санының көбейтіндісі
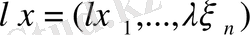 түрінде, яғни осы вектордың әрбір координатын
түрінде, яғни осы вектордың әрбір координатын
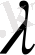 санына көбейтуден пайда болған вектор ретінде анықталады.
санына көбейтуден пайда болған вектор ретінде анықталады.
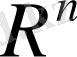 жиынының элементтері үшін анықталған қосу және санға көбейту амалдары векторлардың координаттарына, яғни сандарға қолданылады. Сондықтан жоғарыда келтірілген 1. 1. -1. 2. аксиомаларының орындалуы нақты(комплекс) сандардың қасиеттерінен тікелей шығады. 1. 3 аксиомасындағы нөлдік элемент ретінде
жиынының элементтері үшін анықталған қосу және санға көбейту амалдары векторлардың координаттарына, яғни сандарға қолданылады. Сондықтан жоғарыда келтірілген 1. 1. -1. 2. аксиомаларының орындалуы нақты(комплекс) сандардың қасиеттерінен тікелей шығады. 1. 3 аксиомасындағы нөлдік элемент ретінде
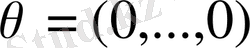 , ал 1. 4. аксиомасына сәйкес
, ал 1. 4. аксиомасына сәйкес
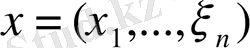 элементіне қарама-қарсы элемент ретінде
элементіне қарама-қарсы элемент ретінде
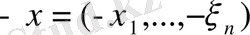 элементі болады.
элементі болады.
Ал, 2. 1. -2. 4. қасиеттері орындалатындығы нақты (немесе комплекс) сандар қасиеттерінен тікелей шығады. Осылай анықталған сызықтық кеңістік
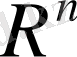 арқылы таңбаланады.
арқылы таңбаланады.
Анықтама.
 ішжиыны өз бетінше сызықтық кеңістік құрайтын болса, онда
ішжиыны өз бетінше сызықтық кеңістік құрайтын болса, онда
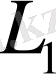 ішжиыны
ішжиыны
 кеңістігінің ішкеңістігі деп аталады.
кеңістігінің ішкеңістігі деп аталады.
Анықтама.
Егер кез келген
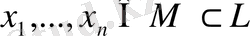 векторлары мен бірге олардың кез келген сызықты комбинациясы да осы
векторлары мен бірге олардың кез келген сызықты комбинациясы да осы
 жиынында жататын болса, онда
жиынында жататын болса, онда
 жиыны сызықтық көпбейнелік деп аталады.
жиыны сызықтық көпбейнелік деп аталады.
Анықтама.
Егер әрбір
 үшін нақты сан мәнді
үшін нақты сан мәнді
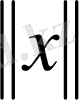 функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
функциясы анықталса және ол мына шарттарды қанағаттандыратын болса:
- және текболғанда ғана(норманың теріс еместік шарты) ;
- Кез келгенсаны үшін(норманың біртектілік шарты) ;
- Кез келгенүшін(үшбұрыш теңсіздігі),
онда
 кеңістігінде норма анықған дейміз.
кеңістігінде норма анықған дейміз.
Анықтамада келтірілген 1), 2), 3) шарттары норманың аксиомалары деп аталады.
Норма анықталған сызықтық кеңістік нормаланған сызықтық кеңістік деп аталады.
Анықтама.
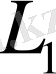 жиынының жеке өзі нормаланған сызықтық кеңістік болып табылады. Осы кеңістік нормаланған сызықтық
жиынының жеке өзі нормаланған сызықтық кеңістік болып табылады. Осы кеңістік нормаланған сызықтық
 кеңістігінің ішкеңістігі деп аталады.
кеңістігінің ішкеңістігі деп аталады.
Нормаланған сызықтық кеңістікке мысал.
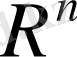 -сызықты кеңістік. Сызықты кеңістікте норма анықтап, оны нормаланған сызықтық кеңістікке айналдырамыз. Мұндағы
-сызықты кеңістік. Сызықты кеңістікте норма анықтап, оны нормаланған сызықтық кеңістікке айналдырамыз. Мұндағы
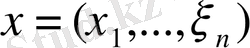 үшін норманы
үшін норманы
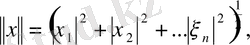 (1. 2. 1)
(1. 2. 1)
теңдігімен анықтаймыз. Бірінші шарттың орындалатыны
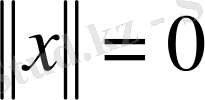 болса, онда барлық
болса, онда барлық
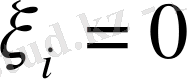 болатыны. Себебі, егер қайсыбір
болатыны. Себебі, егер қайсыбір
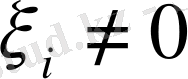 болса, онда (1. 1) теңдігінің оң жағындағы өрнектің мәні оң сан болады. Сонымен, егер
болса, онда (1. 1) теңдігінің оң жағындағы өрнектің мәні оң сан болады. Сонымен, егер
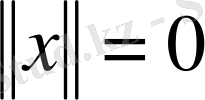 болса, онда
болса, онда
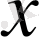 векторының барлық координаттары нөлге тең:
векторының барлық координаттары нөлге тең:
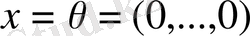 . Керісінше, егер
. Керісінше, егер
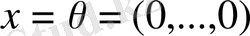 болса, онда
болса, онда
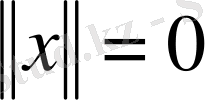 болады.
болады.
Екінші аксиоманы тексерейік:
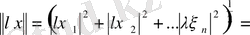
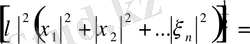
=
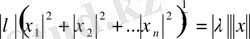
Үшінші аксома, алдымен Коши теңсіздігін алайық. Кез келген
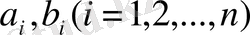 нақты сандары үшін
нақты сандары үшін
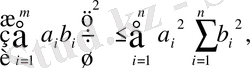 (1. 2. 3)
(1. 2. 3)
теңсіздігі орындалады. Бұл теңсіздіктің екі жағынан квадраттаймыз:
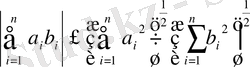 (1. 2. 4)
(1. 2. 4)
Енді осы теңсіздікті пайдаланып (1. 1) нормасы үшін үшбұрыш теңсіздігін дәлелдейміз:
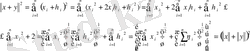
теңсіздігінің екі жағынан квадрат түбір алып, үшбұрыш теңсіздігіне келеміз. Сонымен (1. 1. 1) теңдігімен анықталған норма шынында да норма аксиомаларын қанағаттандырады.
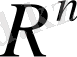 жиыны нормаланған сызықтық кеңістікке айналады. Бұл кеңістік, арифметикалық Евклид кеңістігі деп, ал норма (1. 1. 1) -Евклид нормасы (немесе евклидтік нормасы) деп аталады.
жиыны нормаланған сызықтық кеңістікке айналады. Бұл кеңістік, арифметикалық Евклид кеңістігі деп, ал норма (1. 1. 1) -Евклид нормасы (немесе евклидтік нормасы) деп аталады.
Анықтама. Егер сызықты нормаланған кеңістік
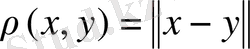
метрикасы бойынша толық метрикалық кеңістік болса онда сызықты нормаланған кеңістік толық деп аталады.
Толық сызықты нормаланған кеңістік банах кеңістігі деп аталады.
Теорема. Әрбір сызықты нормаланған кеңістік қандайда бір банах кеңістігіне енеді және сол кеңістікте тығыз болады.
Сызықтық кеңістіктерде анықталған сызықтық бейнелеулер
L - кез-келген сызықтық кеңістік болсын. Осы кеңістіктің элементтерінде анықталған сан мәнді f(x) функциясы функционал деп аталады.
Мұнда, әдеттегідей, f сәйкестікті анықтайтын ережені, ал f(x) таңбасы х әлементіне сәйкес қойылған санды белгілейді. L кеңістігінің құрылымына қарай f(x) нақты не комплекс мәнді функционал болуы мүмкін.
Мысалы,
f(x)
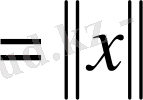 әрқашан нақты мәнді функционал.
әрқашан нақты мәнді функционал.
Егер f(x) функционалы үшін мына екі шарт орындалатын болса:
- Кез-келгенүшінf(x+y) =f(x) +f(y) (аддитивтік шарты) ,
- Кез келгенℷ\gimel
саны үшін
f(
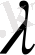 x) =
x) =
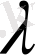 f(x) (
біртектілік шарты), онда
f(x)
сызықтық функционал деп аталады.
f(x) (
біртектілік шарты), онда
f(x)
сызықтық функционал деп аталады.
Бұл екі шартты біріктіріп, мына бір теңдік түрінде қолдануға да болады:
F(αx+βy) =αf(x) +βf(y), (1. 2. 5)
мұнда α және β кез-келген сандар. Бұл теңдік анықтамадағы екі шартқа пара-пар болғандықтан, функционалдың сызықтылығын тексеру үшін (1. 2. 5) теңдігін тексеру жеткілікті.
Сызықтық функционалдардың мысалдарын келтірейік.
L=R n кеңістігінің x= (ξ 1 , …, ξ n ) элементінде f(x) функционалының мәні F(x) =a 1 ξ 1 +…+a n ξ n , (1. 2. 6)
теңдігімен анықталған, мұнда a 1 , …, a n тұрақты сандар. Бұл функционалдың аддитивтік және бартектілік қасиеттерін тексеру оңай. R n кеңістігінде анықталған бұл функционалдың кәдімгі n айнымалылы сызықтық функция екеніне зер аударайық. Кейін R n кеңістігіндегі сызықтық функционал тек осы түрде болатыны айқындалады.
L=C[a, b]
сызықтық кеңістігінде
f(x)
функционалының
x(t)
элементіндегі мәні
f(x) =
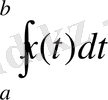 ,
(1. 2. 7)
,
(1. 2. 7)
L=L[a, b]
қосындыланатын функциялар кеңістігінде
f(x)
функционалының
x(t)
элементігіндегі мәні қайсыбір шенелген, тиянақты
a(t)
функциясы арқылы
f(x) =
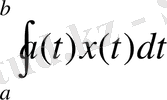 ,
(1. 2. 8)
,
(1. 2. 8)
теңдігімен анықталған. Бұл функционалдың да сызықтық қасиеті интегралдың қасиеттерінен тікелей шығады және бұл (1. 2. 7) функционалының жалпыланған түрі екені де түсінікті.
L=C[a, b]
кеңістігінде анықталған тағы бір функционал
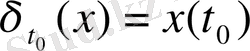 , (1. 2. 9)
, (1. 2. 9)
Яғни
функционалының
x(t
0
)
 элементіндегі мәні
элементіндегі мәні
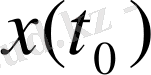 санына тең. Анықтаушы теңдік (2. 5) бойынша
санына тең. Анықтаушы теңдік (2. 5) бойынша
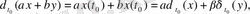
демек бұл сызықтық функционал.
- ∈\in \
L=l
1
сызықтық кеңістігінде
x=(ξ
1
, …, ξ
n
)
l
1
кез-келген, ал
a=(a
1
, …, a
k
, …)
 тиянақты элемент болсын. Функционалды
тиянақты элемент болсын. Функционалды
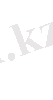
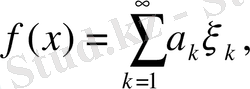 (1. 2. 10)
(1. 2. 10)
теңдігімен анықтайық. Бұл кеңістіктегі элементтерді қосу және элементті санға көбейту амалдары аттас координаттарға қолданылатын болғандықтан, егер α мен β кез-келген сандар, ал
y=(η
1
, …, η
k
,, …)
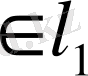 болса, онда
болса, онда
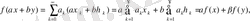
демек, бұл сызықтық функционал.
Ескерту. Егер a=(a 1 , …, a k , …) тізбегін (1. 2. 10) қатары жинақты болатындай етіп алсақ, онда (1. 2. 10) теңдігі басқа да ( l p, c 0 , c ) тізбектер кеңістіктерінде сызықтық функционалды анықтайды.
Мысалы,
a=(a
1
, …, a
k
, …)
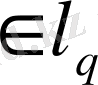 тиянақты, ал
x=(ξ
1
, …, ξ
k
, …)
l
p
кез келген элемент болса, онда, қатарлар үшін Гельдер теңсіздігінің салдарынан, (1. 2. 10) қатары жинақты болады да, (1. 2. 10) теңдігі
l
p
кеңістігінде сызықтық функционал анықтайды.
тиянақты, ал
x=(ξ
1
, …, ξ
k
, …)
l
p
кез келген элемент болса, онда, қатарлар үшін Гельдер теңсіздігінің салдарынан, (1. 2. 10) қатары жинақты болады да, (1. 2. 10) теңдігі
l
p
кеңістігінде сызықтық функционал анықтайды.
 және
және
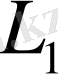 - кез-келген сызықтық кеңістіктер болсын.
- кез-келген сызықтық кеңістіктер болсын.
Анықтама.
Егер әрбір
 элементіне белгілі бір
элементіне белгілі бір
 элементі сәйкес қойылған болса, онда
элементі сәйкес қойылған болса, онда
 кеңістігінде оператор анықталған дейміз.
кеңістігінде оператор анықталған дейміз.
Осы операторды
А
символымен таңбаланса, онда
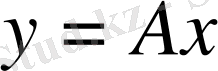 теңдігі
А
операторының
теңдігі
А
операторының
 элементін
элементін
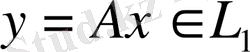 элементін бейнелейтінін көрсетеді. Егер әрбір
элементін бейнелейтінін көрсетеді. Егер әрбір
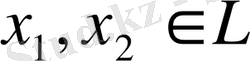 элементтері және кез-келген
элементтері және кез-келген
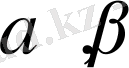 сандары үшін
сандары үшін
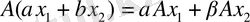 (1. 2. 11)
(1. 2. 11)
теңдігі орындалатын болса, онда А сызықтық оператор деп аталады.
Сызықтық операторлардың мысалдары
1. Нөл-оператор.
 -сызықтық кеністік.
-сызықтық кеністік.
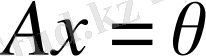 , яғни бұл оператор кеңістіктегі кез-келген элементті нөлдік элементке аударады. Сызықтылық шарты (1. 2. 11) теңдігі орындалатынын тексеру оңай.
, яғни бұл оператор кеңістіктегі кез-келген элементті нөлдік элементке аударады. Сызықтылық шарты (1. 2. 11) теңдігі орындалатынын тексеру оңай.
2. Бірлік оператор.
 - кез-келген сызықтық кеністік,
- кез-келген сызықтық кеністік,
 болсын.
болсын.

теңдігімен анықталған
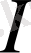 операторы бірлік оператор деп аталады. Бұл оператор кеңістіктің әр элементін осы элементтің өзіне бейнелейді.
операторы бірлік оператор деп аталады. Бұл оператор кеңістіктің әр элементін осы элементтің өзіне бейнелейді.
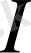 сызықтық оператор екені оның анықтамасынан айқын.
сызықтық оператор екені оның анықтамасынан айқын.
3. Матрица.
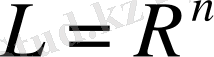 ,
,
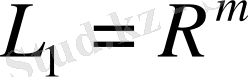 болсын.
болсын.
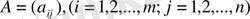 матрица және
матрица және
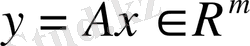 элементі
элементі
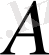 матрицасы мен
матрицасы мен
 векторының көбейтіндісі болсын. Сонда бұл матрица
векторының көбейтіндісі болсын. Сонда бұл матрица
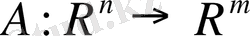 сызықтық операторын анықтайды. Бұл оператордың сызықтық қасиеті матрицалары көбейту ережесінің салдары болады.
сызықтық операторын анықтайды. Бұл оператордың сызықтық қасиеті матрицалары көбейту ережесінің салдары болады.
Шынында да, егер
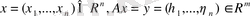 болса, онда матрицаларды көбейту ережесі бойынша
болса, онда матрицаларды көбейту ережесі бойынша
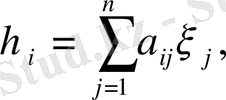 (1. 2. 12)
(1. 2. 12)
Егер
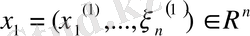 және
және
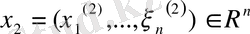 кез-келген екі вектор болса, ал олардың
кез-келген екі вектор болса, ал олардың
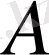 матрицасымен түрленген бейнелері
матрицасымен түрленген бейнелері
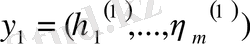 және
және
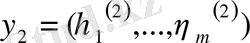
векторлары болса, онда (1. 2. 12) теңдігі бойынша
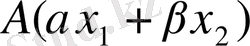 векторының
векторының
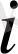 -нші координаты тең:
-нші координаты тең:
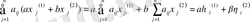 ал, екінші жағынан, бұл
ал, екінші жағынан, бұл
 векторының
векторының
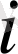 -нші координаты, демек, (1. 2. 11) теңдігімен орындалады.
-нші координаты, демек, (1. 2. 11) теңдігімен орындалады.
Ескерту 1
. Керісінше, кез-келген
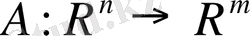 сызықтық операторы матрица арқылы берілгенін дәлелдеуге болады.
сызықтық операторы матрица арқылы берілгенін дәлелдеуге болады.
4. Функцияға көбейту операторы.
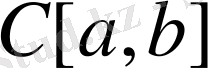 кеңістігінен жеке алынған тиянақты
кеңістігінен жеке алынған тиянақты
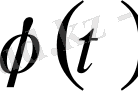 функциясы және кез-келген
функциясы және кез-келген
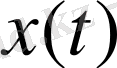 үшін
үшін
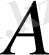 операторы
операторы
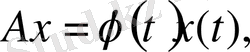 (1. 2. 13)
(1. 2. 13)
теңдігімен анықталған болсын. Бұл
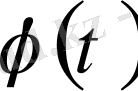 функциясына көбейту операторы деп аталады. Бұл
функциясына көбейту операторы деп аталады. Бұл
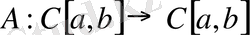 сызықтық оператор екені айқын.
сызықтық оператор екені айқын.
5. Интегралдық оператор.
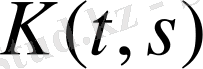 функциясы
функциясы
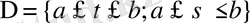 квадратында үздіксіз болсын. Кез-келген
квадратында үздіксіз болсын. Кез-келген
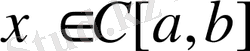 функциясы үшін операторды
функциясы үшін операторды
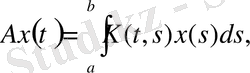 (1. 2. 14)
(1. 2. 14)
теңдігімен анықтайық. Онда
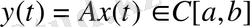 , яғни (1. 2. 14) теңдігімен
, яғни (1. 2. 14) теңдігімен
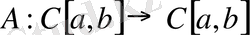 операторы анықталды. Интегралдың сызықтық қасиетінен бұл оператордың да сызықтық оператор екендігі тікелей шығады.
операторы анықталды. Интегралдың сызықтық қасиетінен бұл оператордың да сызықтық оператор екендігі тікелей шығады.
Ескерту 2.
Егер
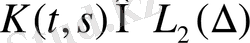 болса, онда (1. 2. 14) теңдігі
болса, онда (1. 2. 14) теңдігі
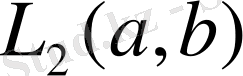 кеңістігінде сызықтық оператор анықтайды, яғни бұл жағдайда
кеңістігінде сызықтық оператор анықтайды, яғни бұл жағдайда
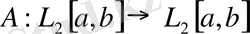
Операторларға қолданылатын амалдар. Сызықтық кеңістікте анықталған операторларға қосу, көбейту және операторды санға көбейту амалдарын қолданып, жаңа сызықтық оператор анықтауға болады. Осы айтылған амалдарды анықтайық.
Операторларды қосу.
Егер
 сызықтық кеңістігінде А және В сызықтық операторлары анықталған болса, онда олардың қосындысы
сызықтық кеңістігінде А және В сызықтық операторлары анықталған болса, онда олардың қосындысы
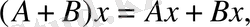 (1. 2. 15)
(1. 2. 15)
теңдігімен анықталады, яғни қосынды оператор әрбір х элементін осы элементтің бейнелерінің қосындысына аударады.
Операторды санға көбейту
.
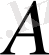 операторының
операторының
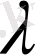 санына көбейтіндісі, яғни
санына көбейтіндісі, яғни
 операторы
операторы
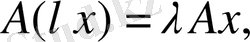 (1. 2. 16)
(1. 2. 16)
теңдігімен анықталады.
 операторы
операторы
 кеңістігінде анықталған болса, онда
кеңістігінде анықталған болса, онда
 да осы кеңістікте анықталғандығы айқын.
да осы кеңістікте анықталғандығы айқын.
Операторлардың бірін екіншісіне көбейту.
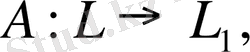 ал
В
операторы
ал
В
операторы
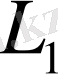 кеңістігінде анықталған. Енді
ВА
операторы
(ВА) х=В(Ах),
(1. 2. 17)
кеңістігінде анықталған. Енді
ВА
операторы
(ВА) х=В(Ах),
(1. 2. 17)
теңдігімен анықталады. Бұл анықтама қисынды болуы үшін ВА көбейтіндісінде бірінші тұрған оператордың мәндері екінші оператордың анықталу жиынында жатуы шарт.
Егер А және В сызықтық операторлар болса, онда (1. 2. 15) -(1. 2. 17) теңдіктерімен анықталған операторлар да сызықтық операторлар екенін тексеру қиын емес. Мысалы, ВА оперторының сызықтық қасиетін тексерейік:

Оператордың дәрежелері.
Егер
А
операторы
 кеңістігінде анықталған және оның мәндері
Ах
осы кеңістікте жататын болса, онда
А
операторының дәрежелері
кеңістігінде анықталған және оның мәндері
Ах
осы кеңістікте жататын болса, онда
А
операторының дәрежелері
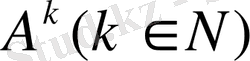 келесі түрде анықталады:
келесі түрде анықталады:
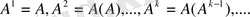
Кері оператор.
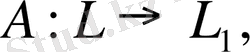 сызықтық операторы берілсін. Оның мәнінің жиынын
сызықтық операторы берілсін. Оның мәнінің жиынын
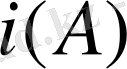 символымен белгілейік және оны
А
операторының бейнесі деп атаймыз. Басқаша айтқанда,
символымен белгілейік және оны
А
операторының бейнесі деп атаймыз. Басқаша айтқанда,
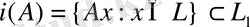 жиыны. Егер
жиыны. Егер
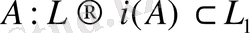 сәйкестігі биекция болса, яғни әрбір
сәйкестігі биекция болса, яғни әрбір
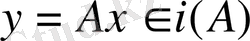 элементіне тек
элементіне тек
 элементі сәйкес қойылған болса, онда бірмәнді
элементі сәйкес қойылған болса, онда бірмәнді
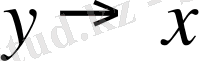 бейнелеуі анықталады. Осы операторы
бейнелеуі анықталады. Осы операторы
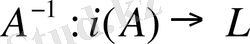 түрінде таңбаланады және ол
А
операторына кері оператор деп аталады.
түрінде таңбаланады және ол
А
операторына кері оператор деп аталады.
1. 3. Гильберт кеңістігі
Анализде функциялардың скаляр көбейтіндісі кеңінен қолданылады. Сондықтан скаляр көбейтінді енгізілген сызықты кеңістікті қарастырған жөн болады.
Анықтама.
Айталық
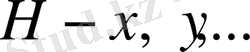 элементтерінің қандай да бір жиыны болсын.
элементтерінің қандай да бір жиыны болсын.
I. Егер
 жиынында
жиынында
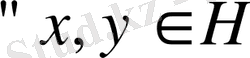 үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
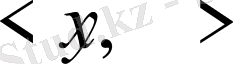 енгізілсе:
енгізілсе:
1.
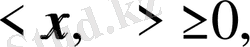 және
және
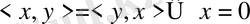
2.
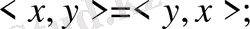
3.
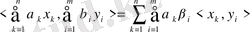 ;
;
II.
 жиынында
жиынында
 үшін
n
сызықты тәуелсіз векторлар табылса, яғни
үшін
n
сызықты тәуелсіз векторлар табылса, яғни
 ақырсыз өлшемді болса, онда
ақырсыз өлшемді болса, онда
 абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
Гильберт кеңістігінде элементінің нормасы
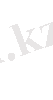

арқылы енгізіледі.
Бұл өрнекпен енгізілген
 элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
Гильберт кеңістігінде
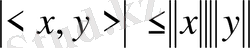
теңсіздігі орынды болады. Бұл теңсіздік Коши-Буняковский-Шварц теңсіздігі деп аталады.
Гильберт кеңістігінде метрика

теңдігі бойынша анықталады және осы метрика мағынасында Н толық кеңістік болып табылады.
Егер
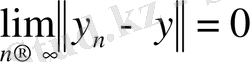
және
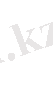
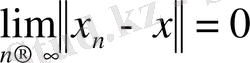 болса, онда
болса, онда
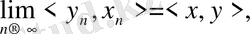
яғни скаляр көбейтіндінің үзіліссіздігі орынды.
Гильберт кеңістігіне мысал
1 0 . H=l 2 координаттық Гильберт кеңістігі. Бұл кеңістіктің элементтері ретінде компоненттері
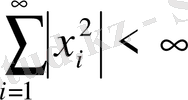
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz