Жоғарғы дәрежелі алгебралық теңдеулерді шешу әдістері және шешімділік теоремалары


Мазмұны
І. Кіріспе . . . 3
І-Тарау. Жоғарғы дәрежелі алгебралық теңдеулер.
1. 1. Алгебралық теңдеулерді шешу алгоритмдері . . . 5
1. 2. Жалпы теоремелар . . . 9
1. 3. Жоғарғы дәрежелі алгебралық теңдеулерді элементар әдістермен шешу . . . 11
1. 4. Бір айнымалысы бар теңдеулерді жеделдетіп шешу . . . 12
ІІ-Тарау. Алгебралық теңдеулердің шешімділік анықтауышы.
2. 1. Алгебралық теңдеулердің шешімділік теоремалары . . . 21
2. 2 Теңдеудің шешіділік анықтауышын түрлендіру . . . 31
2. 3. Үшінші дәрежелі теңдеудің шешімділігі . . . 35
2. 4. Төртінші дәрежелі теңдеудің шешімділігі . . . 43
ІІ. Қорытынды . . . 60
ІІІ. Пайдаланылған әдебиеттер . . . 61
Кіріспе.
х
3
+рх=q, р, q>0 түріндегі теңдеудің шешімін бірінші рет 1526 жылы профессор Сицион дель Ферро тапқан. Бұл әдіс Фиоре деп аталады. х
3
=р+q р, q>0 түріндегі теңдеудің шешімін ХVІ ғасырда Н. Тартарьи тапқан. Бұл әдіс қазіргі кезде Кардано формуласы деп аталып жүр. Мұнда: х=
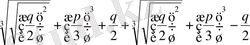 . Н. Тарталья
. Н. Тарталья
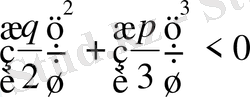 болатын жағдайда шешімін таба алмады. Ол өзінің тапқан шешімі туралы сол кездің философ және математик ғалымы Джироламо Карданоға айтты. 1545 жылы Кардано үшінші дәрежелі теңдеудің толық шешімін талдап «Алгебралық ережелердің ұлы тәсілі» мақаласын жазды. Карданоның оқушысы Л. Феррари төртінші дәрежелі теңдеуді үшінші дәрежелі теңдеуге келтіріп шешті. Бесінші дәрежелі теңдеулер шешімінің жалпы формуласын табу мақсатымен көптеген ғалымдар айналысты. Бірінші, екінші, үшінші, төртінші дәрежелі теңдеулерді шешудің жалпы формулаларында олардың шешімдері қосу, азайту, бөлу және түбірден табу амалдары көмегімен теңдеудің коэфициенттері арқылы өрнектеледі. Осындай мәселені бесінші дәрежелі теңдеу ішінде табуға болады ма деген мәселе туындады. Француз математигі Э. Галуа жүргізген зерттеулер нәтижесінде бұл сұраққа теріс жауап алынды. Яғни алгебралық теңдеудің дәрежесі бесінші және одан жоғарғы болған кезде оның коэфициенттері арқылы жоғарғыда келтірілген бес амал арқылы алатын жалпы формуланың жоқтығы айқындалды. Бұл проблемаларға арналған Галуа зерттеулері «Галуа теориясы» деп аталады. Бұл еңбектің нәтижелері Постиков М. М. «Теория Галуа» еңбектерінде келтірілген. Бесінші және одан жоғарғы дәрежелі теңдеулердің радикалдар арқылы шешудің жалпы формуласы жоқ. Төртіншіден жоғарғы дәрежедегі теңдеулердің шешімін табатын формулаларды анықтаумен көптеген ғалымдар айналысқан. Егер х
1
-дің шешімін біліп айту мүмкін болса, (х- х
1
) сызықты көбейткішті бөлу арқылы теңдеудің дәрежесін 1-ге түсіруге болады.
болатын жағдайда шешімін таба алмады. Ол өзінің тапқан шешімі туралы сол кездің философ және математик ғалымы Джироламо Карданоға айтты. 1545 жылы Кардано үшінші дәрежелі теңдеудің толық шешімін талдап «Алгебралық ережелердің ұлы тәсілі» мақаласын жазды. Карданоның оқушысы Л. Феррари төртінші дәрежелі теңдеуді үшінші дәрежелі теңдеуге келтіріп шешті. Бесінші дәрежелі теңдеулер шешімінің жалпы формуласын табу мақсатымен көптеген ғалымдар айналысты. Бірінші, екінші, үшінші, төртінші дәрежелі теңдеулерді шешудің жалпы формулаларында олардың шешімдері қосу, азайту, бөлу және түбірден табу амалдары көмегімен теңдеудің коэфициенттері арқылы өрнектеледі. Осындай мәселені бесінші дәрежелі теңдеу ішінде табуға болады ма деген мәселе туындады. Француз математигі Э. Галуа жүргізген зерттеулер нәтижесінде бұл сұраққа теріс жауап алынды. Яғни алгебралық теңдеудің дәрежесі бесінші және одан жоғарғы болған кезде оның коэфициенттері арқылы жоғарғыда келтірілген бес амал арқылы алатын жалпы формуланың жоқтығы айқындалды. Бұл проблемаларға арналған Галуа зерттеулері «Галуа теориясы» деп аталады. Бұл еңбектің нәтижелері Постиков М. М. «Теория Галуа» еңбектерінде келтірілген. Бесінші және одан жоғарғы дәрежелі теңдеулердің радикалдар арқылы шешудің жалпы формуласы жоқ. Төртіншіден жоғарғы дәрежедегі теңдеулердің шешімін табатын формулаларды анықтаумен көптеген ғалымдар айналысқан. Егер х
1
-дің шешімін біліп айту мүмкін болса, (х- х
1
) сызықты көбейткішті бөлу арқылы теңдеудің дәрежесін 1-ге түсіруге болады.
Үшінші дәрежелі теңдеу немесе кубтық теңдеудің түрі мынадай: ах 3 + bх 2 + сх +d = 0, а ≠ 0, a, b, c, d - нақты сандар, бұл жерде ах 3 - кубтық, bх 2 - квадраттық, сх - сызықтык және b - бос мүше делінеді. а-коэфициентіне бөлгеннен кейін теңдеу канондық түріне ие болады. Кубтық теңдеудің нақты түрлерінің саны дискриминанттың белгісін тәуелді.
Сызықты көбейткіштерге теңдеудің сол жағын жіктеу. Егер
ax 3 +bх 2 + сх + d = a ( x-ά) ( x- β) ( x- φ) жіктеу табылса онда
ax 3 +bх 2 + сх + d = 0 теңдеуі (ά, β, φ) көп шешімдерге ие. Егер ax 3 +bх 2 + сх + d = a ( x - α) ( x 2 + рх + q) түрінің жіктелуі табылса онда х=α шешімі болады және х 2 + р х + q = 0 квадраттық теңдеудің шешімдері берілген теңдеудің шешімдері болып келеді. Егер теңдеудің бір шешімі белгілі болса, сызықты көбейткішті бөліп шығару мүмкіндігі бар. D < 0 болған жағдайда кубтық теңдеудің үш нақты шешімі болады. Формулаларды қолданған кезде түбірлер комплексті сандар болуы да мүмкін.
Төртінші дәрежелі теңдеу.
аx
4
+bх
3
+ сх
2
+ d х + с = 0 a ≠ 0, а, b, с, d е - нақты сандар. у= х+
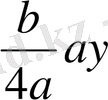 ауыстыруы арқылы берілген теңдеуді келтірілген түрге келтіруге болады, яғни у
4
+ру
2
+qу+r=0, бұл жерде p, g, r коэффициенттер.
ауыстыруы арқылы берілген теңдеуді келтірілген түрге келтіруге болады, яғни у
4
+ру
2
+qу+r=0, бұл жерде p, g, r коэффициенттер.
Бұл теңдеудің шешімі оның кубтық резольвентасының z 3 + 2 pz 2 +(p 2 -4r) z-q 2 =0 шешімінің түріне бағынышты.
Сондықтан дипломдық жұмыстың мақсаты:
Жоғарғы дәрежелі теңдеуді шешудің әдістерін қарастырып оқып үйрену.
І-Тарау
1. 1. Алгебралық теңдеулерді шешу алгоритмдері
Үшінші дәрежелі теңдеу ( кубтық теңдеу) . Үшінші дәрежелі теңдеу немесе кубтық теңдеудің түрі мынадай: ах 3 + bх 2 + сх +d = 0, а ≠ 0, a, b, c, d - нақты сандар, бұл жерде ах 3 - кубтық, bх 2 - квадраттық, сх - сызықтык және b - бос мүше. а-коэфициентіне бөлгеннен кейін теңдеу канондық түрге ие болады:
x
3
+ r х
2
+ sx + t = 0, мұнда r =
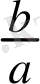 , s =
, s =
 , t =
, t =
 .
.
x
3
+ r х
2
+ sx + t = 0, теңдеуінде у = x+
 ( х = у-
( х = у-
 ) деп ауыстырсақ келтірілген деп аталатын теңдеуді аламыз. у
3
+ ру
3
+ q = 0 бұл жерде
) деп ауыстырсақ келтірілген деп аталатын теңдеуді аламыз. у
3
+ ру
3
+ q = 0 бұл жерде
р =
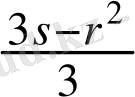 , q =
, q =
 кубтық теңдеудің нақты түрлерінің саны дискриминанттың белгісіне тәуелді.
кубтық теңдеудің нақты түрлерінің саны дискриминанттың белгісіне тәуелді.
D=
 +
+
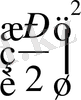 .
.
Екі
комплексті шешімдер
бір нақты шешім және бір нақты екі
шешім және бір нақты үш
шешім (соңғысы егер p =q = 0)
Кубтық теңдеулер.
- Бірінші әдіс.
Сызықты көбейткіштерге теңдеудің сол жағын жіктеу. Егер ax 3 +bх 2 + сх + d = a ( x-ά) ( x- β) ( x- φ) жіктеу табылса, онда
ax 3 +bх 2 + сх + d = 0 теңдеуі (ά, β, φ) шешімдерге ие. Егер ax 3 +bх 2 + сх + d = a(x-α) (x 2 + рх + q) түрінің жіктелуі табылса, онда х=α шешімі болады және х 2 + р х + q = 0 квадраттық теңдеудің шешімдері берілген теңдеудің шешімдері болып келеді. Бұл жағдайда бір шешіміміз х 1 = 0, ал басқа екеуі х 2 + р х + q = 0 квадраттық теңдеудің шешімдері болып келеді.
Егер теңдеудің бір шешімі белгілі болса, сызықты көбейткішті бөліп шығару мүмкіндігі бар.
Мысалы: х 3 + 2 х 2 - 3х - 10 = 0 теңдеуінің шешімін табу. Теңдеуді өзгертіп мына түрінде жазайық:
х 3 - 2 х 2 + 4х 2 -8 х + 5х - 10 = х 2 (х- 2) +4 х( х- 2) + 5 (х - 2) = (х - 2) ( х 2 + 4х +5 ) = 0.
Бұл жерден х
1
= 2; х
3, 2
= - 2±
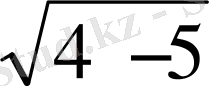 = - 2 ±
= - 2 ±
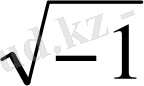 = -2 ± і
= -2 ± і
- Екінші әдіс.
Тартальи - Кардано формуласын қолдану . x 3 + r х 2 + sx + t = 0 кубтық теңдеудің формуласын оның келтірілген түрі у 3 + р у + q = 0 . Бұл жағдайда y 1 = u + v
у
2
=-
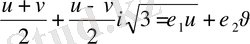 у
3
=-
у
3
=-
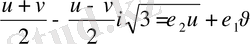 бұл жерде
бұл жерде
U = -
 ; υ=-
; υ=-
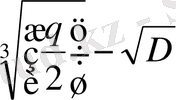 ; D =
; D =
 +
+
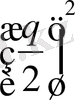 ; E
1. 2
=
; E
1. 2
=
 .
.
х
k
= у
k
-
 (k= 1. 2. 3) ауыстыру арқылы у
к
- дан x
3
+ r х
2
+ sx + t = 0, кубтық теңдеудің шешімін аламыз.
(k= 1. 2. 3) ауыстыру арқылы у
к
- дан x
3
+ r х
2
+ sx + t = 0, кубтық теңдеудің шешімін аламыз.
D < 0 болған жағдайда кубтық теңдеудің үш нақты шешімі болады. Жоғарғыда келтірілген формулаларды қолданған кезде түбірлер комплексті сандар болуыда мүмкін. Р
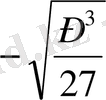 , cos φ =
, cos φ =
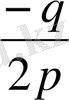 деп алайық, мұнда келтірілген у
3
+ р у + q = 0 теңдеудің шешімі болады: у
1
= 2
деп алайық, мұнда келтірілген у
3
+ р у + q = 0 теңдеудің шешімі болады: у
1
= 2
 ;
;
у
2
= 2
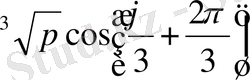 ;
у
3
= 2
;
у
3
= 2
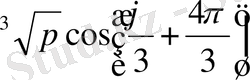 ;
олардың х
k
= у
k
-
;
олардың х
k
= у
k
-
 - ті ауыстыруы арқылы берілген кубтық теңдеудің шешімдеріне қайтып келуге болады.
- ті ауыстыруы арқылы берілген кубтық теңдеудің шешімдеріне қайтып келуге болады.
Мысалы: Тартальи-Кардано формулаларыменен х 3 -9х-28=0 теңдеуінің түбірлерін табу. Бұл теңдеу үшін:
D =
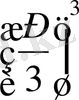 +
+
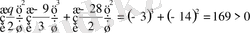
Сондықтан х
3
-9х -28 = 0 теңдеуінің бір нақты шешімі х
1
=4 және екі комплексті х
2
=-2 + і
 ; х
3
=-2 - і
; х
3
=-2 - і
 шешімдері бар.
шешімдері бар.
Төртінші дәрежелі теңдеу мынадай болып келеді:
аx
4
+bх
3
+ сх
2
+ d х + с = 0 a ≠ 0, а, b, с, d е - нақты сандар. у= х+
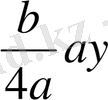 ауыстыруы арқылы берілген теңдеуді төмендегі түрге келтіруге болады, яғни у
4
+ р у
2
+ qу + r = 0, бұл жерде p, g, r коэффициенттер.
ауыстыруы арқылы берілген теңдеуді төмендегі түрге келтіруге болады, яғни у
4
+ р у
2
+ qу + r = 0, бұл жерде p, g, r коэффициенттер.
Бұл теңдеудің шешімі оның кубтық резольвентасының
z 3 + 2 pz 2 +(p 2 -4r) z-q 2 =0 шешімінің түріне бағынышты.
Егер белгісіздің өзгеру аумағы комплексті сандар К болса, нәтиже мынадай
болады:
Төртінші дәрежелі теңдеулер
Бірінші әдіс . Сызықты көбейткішке жіктеу. Егер көпмүшелікті
ax 4 +bх 3 + сх 2 + d х + с = а (х- ά) (х -β) (х-φ) (х-δ) жіктеу мүмкін болса
ax 4 +bх 3 + сх 2 + d х + с = 0 теңдеуі (ά, β, φ) шешімімдерге ие болады. Төртінші дәрежедегі теңдеудің сол жағын екі квадраттық көбейткіштерге жіктеу жеткілікті болар еді. Бұл кезде 4-ші дәрежедегі теңдеудің шешілуі екі квадраттық теңдеудің шешілуіне келер еді.
Екінші әдіс. Егер z 1 , z 2 , z 3 - кубтық резольвентасының
z 3 + 2 pz 2 +(p 2 -4r) z-q 2 =0 түбірі болса, онда:
у
1
=
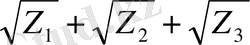 /2
/2
у
2
=
 /2
/2
у
3
=
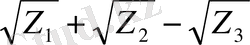 /2
/2
у
4
= -
 /2 - келтірілген у
4
+ ру
2
+ qу + r = 0 теңдеуінің шешімдері бұл жерде
/2 - келтірілген у
4
+ ру
2
+ qу + r = 0 теңдеуінің шешімдері бұл жерде
 радикалдарының алдындағы белгілерін
радикалдарының алдындағы белгілерін
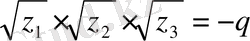 нәтижеге сәйкес алынады. Одан кейін х= у-
нәтижеге сәйкес алынады. Одан кейін х= у-
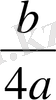 -ны ауыстыру арқылы бастапқы ax
4
+bх
3
+ сх
2
+ d х + с =0 теңдеуінің шешімдерін табады.
-ны ауыстыру арқылы бастапқы ax
4
+bх
3
+ сх
2
+ d х + с =0 теңдеуінің шешімдерін табады.
Мысалы: x 4 -25х 2 + 60х + 36 =0 теңдеуінің кубтық резольвентасы z 3 + 2(-25) z 2 +(-25 ) 2 - 4 (-36) z-60 2 = z 3 -50 z 2 + 769 z - 3600 =0 шешімдеріменен Z 1 =9,
Z
2
=16,
Z
3
=25 сонымен қатар
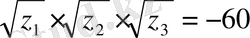 . Радикалдардың алдындағы белгілерді теріс сан етіп алуымыз керек, бұл жерде
. Радикалдардың алдындағы белгілерді теріс сан етіп алуымыз керек, бұл жерде
 x
4
-25х
2
+ 60х +-36 =0 теңдеуінің түбірлері: х
1
= -6, х
2
=3, х
3
=2, х
4
=1.
x
4
-25х
2
+ 60х +-36 =0 теңдеуінің түбірлері: х
1
= -6, х
2
=3, х
3
=2, х
4
=1.
Егер ax 4 +bх 3 + сх 2 + d х + с = 0 теңдеуінде b=а=с болса, онда бұл биквадраттық ax 4 + сх 2 + с = 0 теңдеуі болады. х 2 =t -ні ауыстыруы арқылы бұл теңдеу аt 2 +сt +с = 0 квадраттық теңдеуге айналады. Бұл жерде теңдеудің t 1 , t 2 шешімдері х 2 =t етіп алғанда, бастапқы ax 4 + сх 2 + с = 0 теңдеуінің шешімдері болып табылады.
х
1, 2
=
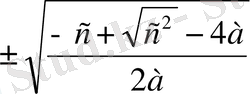 :
:
х
3, 4
=
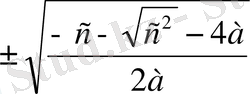 :
:
Егер x 4 +rx 3 +sx 2 +tx+w=0 теңдеуінің коэффициенттері r 3 +8t=4rs катынасын қанағаттандырса бұл теңдеуді квадраттық теңдеуінің көмегімен шешуге болады.
x
4
+rx
3
+sx
2
+t x+w = (x
2
+
 x)
2
+ (s -
x)
2
+ (s -
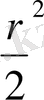 ) (x
2
+
) (x
2
+
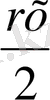 ) +w =0, x
2
+
) +w =0, x
2
+
 = у
= у
ауыстырғаннан кейін 4-ші дәрежелі теңдеу:
у
2
+(s -
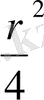 ) у+ w =0 теңдеуіне айналады, оның шешімдерінің негізінде бастапқы теңдеудің шешімдері табылады.
) у+ w =0 теңдеуіне айналады, оның шешімдерінің негізінде бастапқы теңдеудің шешімдері табылады.
Мысалы: x 4 +2 x 3 +9x 2 +8 x+25 =0
x
4
+2 x
3
+9x
2
+8 x+25 = (х
2
+х)
2
+ (9+
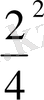 ) (х
2
+х) +25 = (х
2
+х)
2
+8(х
2
+х) +25=0
) (х
2
+х) +25 = (х
2
+х)
2
+8(х
2
+х) +25=0
Бұл жерден: х
2
+х= -4
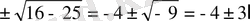
Сондықтан х
1
=-
 і ; х
2
=-
і ; х
2
=-
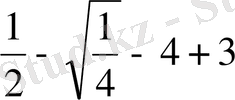 і;
і;
х
3
=-
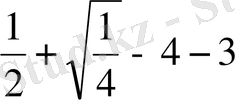 і ;
і ;
х
4
=-
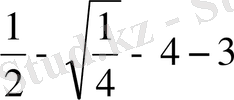 і.
і.
Жоғарғы дәрежелі теңдеулердің дербес түрлері.
Муавр теоремасының көмегімен екі мүшелік х m = a (m > 1, a > 0),
x 1 , x 2 , …. ., x m - m - шешімдері мынандай түрде табылады:
х
к+1
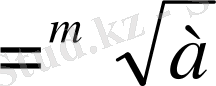 ( cos
( cos
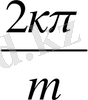 + i sin
+ i sin
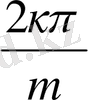 ), бұл жерде ( к =0, 1, 2 . . . , m- 1 )
), бұл жерде ( к =0, 1, 2 . . . , m- 1 )
х 2 m + ах m +в =0 теңдеуі x m =у айнымалы шаманы ауыстыру арқылы квадраттық у 2 +ау+ в=0 теңдеуіне келтіруге болады. Егер ол у 1 , у 2 шешімдеріне ие болса, бастапқы теңдеулердің түбірлерін х m = у 1 , х m = у 2 екімүшелік теңдеуінің көмегімен табылады.
1. 2. Жалпы теоремелар
Егер х 1 - х n + a 1 x n-1 + a 2 x n-2 + …. + a n-1 x+ a n =0 теңдеуінің түбірі болса, онда көп мүшелік Р n (х) теңдеудің сол жағында тұратын (х-х 1 ) қалдықсыз бөлінеді және ол көп мүшелік Р n-1 (х) (n-1) дәрежедегі Р n (х) =(х-х 1 ) Р n-1 (х) Жалпы жағдайда Р n (х) (х-х 1 ) бөлгенде қалдығы Р n (х) болады:
Р n (х) = (х-х 1 ) Р n-1 (х) + Р n (х 1 ) . Егер Р n (х) = (х-х 1 ) к - ге қалдықсыз бөлінсе, бірақ (х-х 1 ) к -1 бөлінбесе, онда х 1, к- еселік Р n (х) =0 теңдеуінің түбірі деп айтылады бұл жағдайда х 1 дегеніміз Р n (х) полиномының және оның туындыларының (к-1) дейін жалпы түбірі.
Алгебраның негізгі теоремасы
Әрбір n - дәрежелі х
n
+а
1
х
n-1
+ а
2
х
n-2
+ . . . + а
n-1
х +а
n
= 0 алгебралық теңдеулер, а
і
(і = 1, 2, …n) коэффициенттері нақты немесе комплексті сандар - n - түбірлері болады, егер к - еселі түбірді к-ға тең түбірлер деп есептесек. Егер Р
n
(х) көпмүшеліктің түбірлері х
1
, х
2
, …. х
і
- ге тең болса, соған сәйкес а
1
, а
2
, …, а
і
(
 ) - ге тең болса теңдеуді мынадай көбейтінді түрінде көрсетуге болады: Р
n
(х) = 0 теңдеуінің шешімін жеңілдетуге болады, егер біреселі Р
n
(х) = 0 теңдеуімен түбірлері бір теңдеуге көшсе Р
n
(х) = 0 көп еселік түбірлер. Сонымен қатар Р
1
n
(х) туындыларының түбірлері болады және көп мүшелікті Р
n
(х), Р
1
n
(х) деп белгілейді. Сол кезде Q(x) =0 теңдеуінің түбірлері Р
n
(х) = 0 бірдей
) - ге тең болса теңдеуді мынадай көбейтінді түрінде көрсетуге болады: Р
n
(х) = 0 теңдеуінің шешімін жеңілдетуге болады, егер біреселі Р
n
(х) = 0 теңдеуімен түбірлері бір теңдеуге көшсе Р
n
(х) = 0 көп еселік түбірлер. Сонымен қатар Р
1
n
(х) туындыларының түбірлері болады және көп мүшелікті Р
n
(х), Р
1
n
(х) деп белгілейді. Сол кезде Q(x) =0 теңдеуінің түбірлері Р
n
(х) = 0 бірдей
Р
n
(х) = х
n
+а
1
х
n-1
+ а
2
х
n-2
+ . . . + а
n-1
х +а
n
= (х-х
1
)
 (х-х
2
)
(х-х
2
)
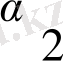 (x-x
r
)
(x-x
r
)
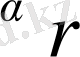 = 0.
= 0.
Нақты коэффициентті теңдеулер.
Егер нақты коэффициентті Р n (х) =х n +а 1 х n-1 + а 2 х n-2 + . . . + а n-1 х +а n = 0 теңдеуі х 1 = ά + і β комплексті түбіріне ие болса, оның х 2 = х 1 = ά - і β түбірі болады және де оның еселігі х 1 -дің еселігіне тең болып келеді. Сондықтан нақты коэффициенттері бар теңдеулердің комплексті түбірлер саны әр дайым жұп болады. Нәтижесінде тақ дәрежелі нақты коэффициенттері бар теңдеу кемінде бір нақты түбіріне ие болады.
Виет теоремасы.
х n +а 1 х n-1 + а 2 х n-2 + . . . + а n-1 х +а n =0 теңдеуі үшін оның түбірлері мен коэффициенттері а і (і= 1, 2, 3 . . . , n) арасында орын алады.
х
1
+х
2
+ . . . +х
n
=
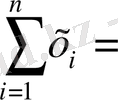 - а
1
, х
1
∙х
2
+ х
1
∙х
3
+ . . . + х
n-1
х
n
=
- а
1
, х
1
∙х
2
+ х
1
∙х
3
+ . . . + х
n-1
х
n
=
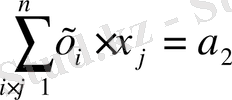 , і<j,
, і<j,
х
1
∙x
2
∙x
3
+ х
1
∙x
2
∙x
4
+…+x
n-2
∙x
n-1
∙x
n
=
 і<j<к,
і<j<к,
х 1 ∙x 2 . . . х n =(-1) n a n
Виет теоремасы квадраттық және кубтық теңдеулер үшін
x 1 + x 2 = -р
х 1 ∙ x 2 = q
х 1 + x 2 + x 3 = - r
х 1 ∙ x 2 + x 1 ∙ x 3 = s
х 1 ∙ x 2 ∙ x 3 = -t
1. 3. Жоғарғы дәрежелі алгебралық теңдеулерді элементар әдістермен шешу.
Теңдеудің алгебралық шешілу жолы мынадай: алгебралық әрекеттер арқылы теңдеудің түбірлерін, мәндерін оның коэффициенттері ретінде формула құрастыру. Теңдеудің алгебралық шешімі дегеніміз ол теңдеулерді радикалдармен шешу, өйткені жалпы формула n >1 дәрежелі теңдеудің түбірлерін коэффициенттер арқылы сипаттаумен қатар, міндетті түрде түбірлерді шығару әрекеттері болуы керек. Расында n >1 дәрежелі теңдеуді шешу формуласы барлық n-түбірлерді табуы тиіс. Егер бұл формулада радикалдар болмаса, ол коэффициенттерге қатысты рационалдық сипаттау болар еді. Сондықтан рационалдық операциялардың қасиетіне қарай, n - түбірлерін емес, тек бір түбірін есептеуге болар еді. Жалпы негізінде радикалдармен төртінші дәредеден аспайтын теңдеулерді шешуге болады. Бесінші және одан жоғарғы дәрежелі теңдеулер радикалдар арқылы шешудің формуласы жоқ. Жалпы түрде радикалдармен төртінші дәрежеден аспайтын теңдеулерді шешуге болады. Жоғарғы дәрежелі теңдеулердің дербес түрлерін радикалмен шешу мүмкін. Теңдеулерді шешу практикасында дербес әдістерді қолдана білу үлкен маңызға ие. Р(х), х- аргументінен шығатын берілген көп мүшелік болсын, және Р(х) көп мүшелік Р (х) = Р 1 (х) Р 2 (х) . . . Р n (х) белгілі дейік, онда Р(х) =0 теңдеуін шешу үшін Р 1 (х) =0, Р 2 (х) =0 . . . Р n (х) =0 теңдеулерінің әрқайсысын шешу жеткілікті. Р(х) =0 теңдеу Р 1 (х) =0, (i=1, 2, …n) теңдеулердің түбірлерінің біріктіруімен алынады. Егер белгілі әдістерді қолдана отырып Р(х) көп мүшелікті көбейткіштерге жіктеуге мүмкін болса, онда Р(х) =0 теңдеуінің шешімдері төмен дәрежелі бірнеше теңдеулердің шешімдеріменен теңеседі.
Мысал 1. х 4 - 2х 3 + 5х 2 - 4х -12 = 0 бұл теңдеуді мынадай түрінде жазайық:
х 4 - 2х 3 + 5х 2 - 4х -12 = х 3 ( х- 2) + 5х (х-2) + 6 (х -2) = (х 3 +5х + 6) (х -2) = (х+1) (х-2) (х 2 -х+6) =0, х 3 + 5х + 6х= (х +1 ) (х 2 - х+6)
Бұдан: х
1
= -1, х
2
= 2, х
3, 4
=
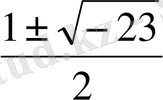
Мысал 2. х 8 -1 = 0 х 8 -1 = (х 4 ) 2 -1 = (х 4 -1 ) (х 4 +1 ) =( х 2 -1) (х 2 +1)
(х
2
+
 ) (х
2
-
) (х
2
-
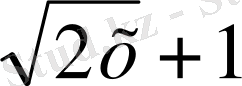 ) = (х - 1) ( х + 1 ) (х
2
+1) (х
2
+
) = (х - 1) ( х + 1 ) (х
2
+1) (х
2
+
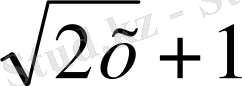 ) (х
2
-
) (х
2
-
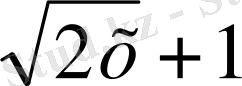 ) = 0
(1)
) = 0
(1)
х
4
+1= (х
4
+ 2 х
2
+1 ) - 2 х
2
=( х
2
+1)
2
- 2 х
2
= (х
2
+1 )
2
- (
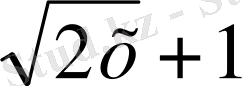 )
2
=
)
2
=
( х
2
+1 +
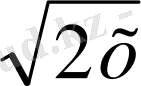 ) ( х
2
+1 -
) ( х
2
+1 -
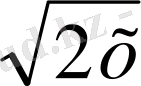 ), бұл жерде (1) -ден табамыз:
), бұл жерде (1) -ден табамыз:
х
1
= 1, х
2
= -1, х
3
= -і, х
4
= і, х
5, 6
=
 , х
7, 8
=
, х
7, 8
=
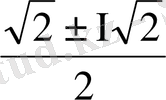 шығады.
шығады.
1. 4. Бір айнымалысы бар теңдеулерді жеделдетіп шешу.
Теңдеудің бүтін түбірлі шешімділігінің анықтауышы.
Бір айнымалысы бар теңдеу берілген:
 х
n
+а
1
х
n-1
+ а
2
х
n-2
+ а
3
х
n-3
+ . . . + а
n-2
х
2
+а
n-1
х+а
n
= 0
х
n
+а
1
х
n-1
+ а
2
х
n-2
+ а
3
х
n-3
+ . . . + а
n-2
х
2
+а
n-1
х+а
n
= 0
а n-1 ; а n коэффициентінің анықтауышын табамыз:
Берілген теңдеуді келесі түрде жазамыз:
а n-1 х +а n =- (х n +а 1 х n-1 + а 2 х n-2 + а 3 х n-3 + . . . + а n-2 х 2 )
Берілген теңдіктің шешімі келесі түрде болады.
а
n-1
х =- (х
n
+а
1
х
n-1
+ а
2
х
n-2
+ а
3
х
n-3
+ . . . + а
n-2
х
2
)
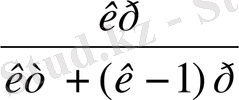
а
n
=- (х
n
+а
1
х
n-1
+ а
2
х
n-2
+ а
3
х
n-3
+ . . . + а
n-2
х
2
)
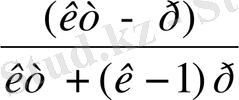
Егер х = km + (k-1) p, бұдан аламыз:
а n-1 = - [[ km +(k-1) p ] n-2 + a 1 [[ km +(k-1) p ] n-3 + a 2 [[ km +(k-1) p ] n-4 +a 3 [[ km +(k-1) p ] n-5 +… + а n-2 ] kp
а n = - [[ km +(k-1) p ] [[ km +(k-1) p ] n-2 + a 1 [[ km +(k-1) p ] n-3 +a 2 [[ km +(k-1) p ] n-4 +… + а n-3 [[ km +(k-1) p ] n-5 + … + а n-2 ] (km-p)
а
n
k а
n-1
шамасының қатынасын табамыз, а
n
≠ 0, а
n-1
≠ 0, болса, одан аламыз:
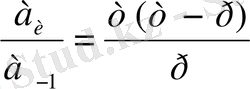 (1) егер к =1
(1) егер к =1
а n-1 = - [m n-2 +a 1 m n-3 + a 2 m n-4 + a 3 m n-5 + …+ a n-2 ] p (2)
а n = -m[m n-2 +a 1 m n-3 + a 2 m n-4 + a 3 m n-5 + …+ a n-2 ] (m-p) (3)
(1) -ден
аламыз: Р =
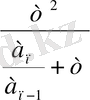 (4)
(4)
(2), (3), (4) теңдіктер осы теңдеудің анықтауышы болады.
Бір айнымалы теңдеудің шешімін тауып және бүтін сандар теңдеуінің шешімін зерттеу қажет. Егер а 1 , а 2 , а 3 , . . . , а n-1 , a п - бүтін сандар балса. (2) -ші теңдеуден:
- Егер мұндағы m, , р бүтін сан болса, онда теңдеудің шешімі бүтін сан болады. Нақты жауап алу үшін (4) - ші формуладан р - ті тексеру керек. Егер р-шамасы аn-1формуласының анықтауышы (4) - ші формуладағы р- шамасымен сәйкес келсе, онда бүтін сандар теңдеудің шешімі болады. Егер сәйкес келмесе онда бүтін сандар теңдеудің шешімі болмайды.
- аn-1формуласынан р жәнетшамасын анықтап және алынған шаманы аnформуласына қойсақ, онда берілген аnшамасына сәйкес келеді. Берілген аnшамасына сәйкес келетін осы теңдеудің шешімі болатынтшамасын аламыз. Бір айнымалы теңдеудің шешіміне қатысты 2, 3, 4 анықтауышқа байланысты мысал келтірейік.
Мысал 1. х 3 +а 1 х 2 +а n-1 х+а n =0
Берілген теңдеуден жалпы формуланы табамыз:
а n = -m [m +a 1 ] (m- p)
а n-1 = - [m +a 1 ] p
Р=

а n , а n-1, р-формуласынан кез-келген үшінші дәрежелі теңдеуді шешуге болады.
а) Шешімі: х 3 +8х 2 +4х+15=0
а 1 =8. а n-1 =4, а n =15
а n-1 = - [m +8] p=4
а n = -m [m +8] (m- p) = 15
Р=
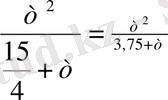
т
шамасының ауданын анықтаймыз. х
3
+8х
2
+4х+15=0 теңдеуінің түбірі болады. Сондықтан
т
шамасының анықтаймыз, егер р шамасына қатысты болса, онда Р=
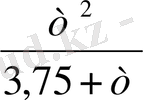 және Р=
және Р=
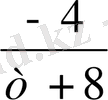 а
n-1
= - [m +8] p=4
а
n-1
= - [m +8] p=4
1. Р > 0
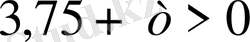
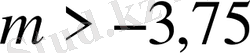
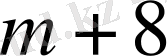 < 0,
< 0,
 <-8 шешімі жоқ
<-8 шешімі жоқ
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz