МАТЕМАТИКА ЖӘНЕ ЭЙЛЕР

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ҚАЗАҚ МЕМЛЕКЕТТІК ҚЫЗДАР ПЕДАГОГИКА ИНСТИТУТЫ

ФИЗИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ

МАТЕМАТИКА КАФЕДРАСЫ

ДИПЛОМДЫҚ ЖҰМЫС

ТАҚЫРЫБЫ: МАТЕМАТИКА ЖӘНЕ ЭЙЛЕР

Орындаған: Күнтуарова Амангуль Маликажқызы

4 жылдық сырттай бөлімінің студенті

Жетекшісі: ф. -м. ғ. д., доцент Қ. К. Шакенов

Қорғауға жіберілді:

Кафедра меңгерушісі ф. -м. ғ. к., доцент А. Қ. Искакова

Хаттама №

Алматы - 2007

МАЗМҰНЫ

Кіріспе . . .

Кіріспе . . .: І. Кейбір математикалық ұғымдардың тарихы

Кіріспе . . .: І. 1. Математика дәуірлері . . .

Кіріспе . . .: І. 2. Математика ұғымдардың қалыптасуы . . .

Кіріспе . . .: ІІ. Эйлердің заманы

Кіріспе . . .: ІІ. 1. XVIII ғасырдың көрнекті математиктері . . .

Кіріспе . . .: ІІ. 2. XIX ғасырдың көрнекті математиктері . . .

Кіріспе . . .: ІІІ. Эйлердің өмір жолы . . .

Кіріспе . . .: ІV. Эйлердің математикаға қосқан үлесі

Кіріспе . . .: IV. 1. Леонард Эйлердің ғылыми еңбектері . . .

Кіріспе . . .: IV. 2. Эйлердің механика ғылымына сіңірген еңбегі . . .

Кіріспе . . .: Қорытынды . . .

Кіріспе . . .: Қосымшалар . . .

Кіріспе . . .: Әдебиеттер . . .

КІРІСПЕ

Қазіргі ғылым, оның іргетасы - математика заманымыздың аса мәдени құбылысы, жалпы өркениетіміздің бөлінбес маңызды бір бөлігі болып отыр. Сондықтан да болашақ математика пәнінің мұғалімдері ғана емес, білім-парасатқаұмтылған әрбір азаматтың ғылым тарихынан, әсірес «ғылым патшасы» математика тарихынан белгілі бір дәрежеде хабардар болуы игілікті нәрсе.

Ғылым тарихын зерттеп білудің ғылымның өзі үшінде маңызы зор. Көрнекті математика тарихшысы Поль Еаннедің сөзімен айтсақ, тарихтың бірден-бір түпкі мақсаты тіпті де бекер әуесқойлықты қанағаттандыру емес, оны зерттеп білу, сайып келгенде, болашақты нұрландыру.

Кейбіреулер математика өте шабын дамитын, тіпті өзгермейтін ғылым деп қарайды. Бұл түбірімен дұрыс емес. Адамзат мұқтаждығын, қоғамдық прогрес талабын өтеу жолында математика ғылымы ұдайы дамып, кемелденіп келеді. Математиканың арифметика, алгебра, геометрия, математикалық анализ сияқты классикалық салаларына қоғам қажеттігін, прогресс талабын өтеу, сондай-ақ математиканың дамуының өзінің ішкі логикалық талаптарын қанағаттандыру арысында функциялық анализ, математикалық логика, математикалық статистика, кибернетика, хабарлар теориясы және толып жатқан жаңа салалардың қосылуы бұл айтқанымызды толық дәлелдейді. Бұл процес қазірде толасыз жүріп жатыр.

Математика өзінің туып, өрбу барысында тарихи дамудың ұзақ жолын басып өтті. Екі нүктенің ең жақын ара қашықтығы түзудің кесіндісі болатыны туралы және ең бастапқы сандар жайлы өте қарапайым білімдерден басталған математика өзінің қазір нақты пәні мақсаты әдіс-тәсілдері бар аса күрделі абстракты ғылымға айналып отыр. «Екі жерде екі төрт» деген шындықты білуден бастап осы күнгі аспан денесінің қозғалысын алдын ала есептеуге (мәселен, Галлей кометасының траекториясын), атым ішіндегі процестердің есебін білуге, саусақпен санау орнына қиялдан да ұшқыр тез есептегіш электронды машиналармен (ЭЕМ) санауға жету үшін адам баласына көп мыңдаған жыл уақыт керек болды.

Диплом жұмысында «барлық замандардың және барлық халықтардың ұлы математигі» деп аталып кеткен ғалым Леонард Эйлер туралы - Эйлердің заманы, Эйлердің өмір жолы, Эйлердің математикаға қосқан үлесі қарастырылған.

Эйлер сол кезде бар математиканың барлық саласы бойынша елеулі табыстарға жеткен. Ол өзінің жаңалықтарын мақала түрде ғана емес, бір жүйеге келтірілген оқу құралдарында да жариялап отырған. Эйлердің кейбір салалардағы баяндауы ғылымның соңғы сөзіндей, кейіннен ол ешбір өгеріске ұшырамаған.

Математика тарихы математиканың бір саласы болып есептеледі. Ол математика дамуының объективтік заңдылықтары туралы ғылым. Осыған сәйкес математика тарихының көп мәселелерді қарастыруына тура келеді. Мектеп оқытушылардың математикаға қызығушылығын арттыру үшін факультатівті сабақтар, математика викторинасын, КВН өткізуде осы диплом жұмысы пайдалығын көрсетеді деген ойдамыз.

І. МАТЕМАТИКАНЫҢ НЕГІЗГІ ҰҒЫМДАРЫНЫҢ ТАРИХЫ

І. 1. Математика дәуірлері

Тарихи-математикалық зерттеулер: 1) математиканың дамуындағы фактілер мен мағлұматтар байлығын ашады; 2) математиканың практикалық мұқтаждығын және адам әрекеттерін, басқа ғылымдардың дамуын, қоғамның әлеуметтік және таптық құрылысы мен қатысын, байланысын ашуға тырысады; 3) математиканың логикалық құрылымының тарихи шарттылығын, оның өзгеру диалектикасын көрсетеді. Белгілі дәрежеде оның болашағын, перспективасын болжауға мүмкіндік береді.

Математика тарихының методологиялық негізі - диалектикалық материализм болып табылады.

Көрнекті математик А. Н. Колмогоровтың таратуы бойынша математика тарихын шартты түрде төрт дәуірге бөлуге болады.

Бірінші дәуір - математиканың туу, математикалық білім-дағдылардың, мағлұматтардың жиналу және қорлану дәуірі. Бұл жазба тарихқа дейінгі санаудан, алғашқы қауымнан басталып математика өзінің белгілі бір зерттеу пәні, мақсаты, әдістері, салалары бар дербес теориялық ғылым болып қалыптасқан (біздің заманымызға дейінгі VI-V ғасырлар) грек математикасына дейін созылады. Бұл дәуірде математикалық негізгі ұғымдар, сандар, фигуралар т, б. қалыптасады.

Екіші дәуір - элементарлық математика дәуірі- біздің заманымызға дейінгі VI-V ғасырлардан басталып біздің заманымыздың XVI ғасырымен аяқталады. Бұл кезеңде математика бүтіндей дерлік тұрақты шамалар қарастырылады. Математиканың арифметика, алгебр, геометрия және тригонометрия деп аталатын дербес салалары пайда болады.

Үшінші дәуір - айнымалы шамалар математикасының туу дәуірі. Бұл кезде математиканың негізгі нысанасы, обьектісі-процестерді, қозғалыстарды зерттеп білу. Бұл дәуір XVII ғасырдағы Декарт, Лейбниц, Ньютонның ашқан математикалық жаңалықтарынан басталып XIX ғасырдың бірінші жартысын қамтиды. Бұл аралықта математиканың бұрынғы салаларына аналитикалық геометрия, дифференциалдық және интегралдық есептеулер, дифференциялдық теңдеулер, ықтималдықтар теориясы сияқты физика-математикалық, техникалық және басқа жоғары оқу орындарында оқытылып жүрген қазіргі математиканың классикалық негізі болып саналатын көптеген салалар қоылады.

Төртінші дәіуір - қазіргі математика дәуірі. Бұл XIX ғасырдың бірінші жартысында ұлы математиктер Н. И. Лобачевский, Э. Галуа ашқан математикалық жетістіктерден басталады. Мұнда математика қамтитын кеңістік пішіндері мен сандық қатынастар мейлінше кеңейеді, бұл тұста сандар ғана емес, вектор, тензор, спинор тәрізді және басқа тектес шамалар қарастырыла бастайды. Кеңістік туралы ұғымның шеңбері кеңейіп, әр түрлі геометриялар (евклидтік емес) ашылады. Алгебраның мазмұны бүтіндей өзгеріске ұшырайды. Математиканың көптеген жаңа салалары қалыптасады. Математиканың өзін тарихи, логикалық және философиялық тұрғыдан негіздеу мәселесі қолға алынады; есептегіш машыналар пайда болады.

І. 2. Математика ұғымдардың қалыптасуы

Карл Гаусс математиканың сан салаларын сарапқа салып келіп арифметиканы математика патшасы деп бағалаған. Ал арифметиканың негізгі ұғымы - сан. Ендеше, сол сан ұғымының қалай пайда болуын ашу, білу-ғылыми методогиянық үлкен проблема.

XIX ғасырға дейін математика тарихы жөнінде қалам тартушы авторлардың көбісі сандар мен сандарға амалдар қолдану әрекетін құдайлар немесе кемеңгер филосовтар шығарған деп түсіндіріп келді. Өткен ғасырдағы ең мықты алгебрашылардың бірі Кронекер «бүтін сандарды құдай жасады, қалған дүниені адам жасады», -дегені мәлім. Ескі аңыздарда сандарды біресе Пифагор, біресе Прометей немесе басқа бір пайғамбар шығарыпты-мыс деген тұжырымдар көп ұшырасады. Бұлардың барлығы, әрине, ғылыми шындыққа келмейтін жаңалық қорытындылар.

Шындығында, арифметиканың өзі айрықша ғылым болып бертінді қалыптасқанмен, оның басты ұғымы-сан ұғымы өте ертеде, адамзат жазу, сызуды білмеген заманда пайда болған.

Адам баласының ең бірінші қолдана білген математикалық амалы санау болды. Тіпті аз ғана санды білетін жабайы тайпалардың өзі көп нәрседен тұратын жиындарды санауға дейін әрекет жасаған. Бұл жағынан қарағанда адам саннан бұрын-ақ «санауды», «түгендеуді» білген деуге болады. Қайта осы санау, түгендеу әрекеттері негізінде сан ұғымы туады, біртіндеп кеңейеді. Ежелгі қазақтар төрт түлік малдарын санамай түгендеуі осының нақты мысалы. Ел аузындағы «түгендеймін санамай» деген сөз тіркесі осыны аңғартады. Осы сияқты олар кейде бір қора қойдың өзін жасына қарай бөліп, әрбір төлді бөлек-бөлек түстеп түгендейтін болған. Бұл, әрине, өте ерте кездегі санау тәртібінен қалған сарқыншақтар.

Түстеп-түгендеу жас балалар әрекетінде де ұшырасады. Мәселен, 2-3 жастағы жас сәби ойыншықтарының түгел, түгел еместігін түсіне қарай біле алады.

Осылай түстеп түгендеу кезінде санауға тиісті нәрселер жиынының (иттер тобы, түйелер келесі немесе бір қора қой, ойыншықтар т. б. ) ерекше бір қасиаті ретінде танылады. Ол қасиет біріншіден, осы жиынның бүтіндігін, тұтастығын, екіншіден, сол нәрселерден құралған басқа жиындармен салыстырғанда аз-көптігін білдіреді.

Алайда, көз мөлшермен санау практикасы адам баласының мұқтаждығын аса қанағаттандыра алмаған. Түстеп санау арқылы түгенделетін заттың көп-аздығы, бары-жоғы ажыратылғанмен, санмен келтірілген басқа негізгі міндеттерді (мәселен, мен 20 қоян әкелдім дегенді білдіру сиқты) орындау мүмкін болмады. Мұндай жағдайда адамдар саусақпен санауға ұмтылған. Торрес бұғазының батыс жағалауын мекендейтін кейбір австралиялық жабайы тайпалар адамның дене мүшелері арқылы 33-ке дейінгі санды өрнектей алады екен. Егер саналатын заттар 33-тен асып кетсе, олар таяқшаларды пайдаланады. Ертеде қойшылар таяқтарына баққан қойының санына сай келетін кертікшелер белгелеу арқылы қойның есеп-қисабын алып отырған.

Бұл қарсаңда да сан тең мөлшерлі жиындардың бәріне ортақ, тұрақты қасиетін көрсететін ерекше математикалық ұғым болып қалыптыса қоймады. Мұнда тек бір жиындағы нәрселер сондай мөлшерлі басқа бір жиынмен ауыстырылады. Мысалы, қорадағы қой саны мен таяқтағы кертік саны мөлшерлес.

Санмен санаудың дамуында тағы да бір нәрсе-тең мөлшерлі жиындар, топтарішінен айрықша біреуін сайлап алу. Мәселен, белгілі бір топта бес нәрсенің барын білдіру үшін бір қолдың саусақтарын көрсету жеткілікті болған. Бұл жерде қол саусақтарының жиыны ерекше жиын түрде қарастырылып, осыған тең мөлшердегі басқа жиындар мөлшерін анықтау негізге алынған. Бір топтың сан мөлшерін екінші топ сан мөлшерімен салыстырып, санау практикасы сан ұғымының қалыптасуындағы басты факторлардың біріне айналады. Санау әрекетіндегі осы беталыстың, бағыттың біртіндеп дамуы нәтижесінде өзара тең мөлшерлі жиындардың ортақ, орнықты мөлшерлік қасиеті ретінде біртіндеп натурал сандар ұғымы қалыптаса бастады.

Сан ұғымы баяу дамыды, сандар шекарасы біртіндеп кеңіді. Тілінде тек бір мен екі сандары ғана бар жабайы тайпалар қазірдің өзінде ішінара кездесіп қалады. Әлгінде айтылған Торрес бұғазының тайпалары 1-ді урапун, 2-ні оказа, 3-ті оказа-урапун, 4-оказа-оказа, 5-ті оказа-оказа-урапун, 6-оказа оказа-окааза деп санаған, одан артық сандарды «көп», «сан жетпес» дейді екен. Осындай сандардың белгілі бір шекарасы баяғыда әр халықта да болған. Мысалы, біраз елдерде жеті саны ең үлкен сан болғандығын көрсететін көптеген сөз тіркестері бар: «жеті өлшеп, бір кес», «жетеу жалғызды күтпес», «соқа айдаған біреу, қасық ұстаған жетеу», «жеті су» т. с. с.

Осы сияқты қазақ тілінде де 40 саны бір кезде сандар шекарасы болғанын сипаттайтын сөздер көп кездеседі, «40 шілтен», «40 уәзір», «30 күн ойын, 40 күн тойы», «Қырық құрақ, қырық жамау», «40 жыл қырғын болса да, ажалды өледі» т. б.

Қоғамдық өндірістің өркендеуі, өндірілген өнімнің молаюы, тайпалар, қауымдар арасындағы саяси-шаруашылық қарым-қатынастардың ұлғаюы санның, оған әр түрлі амалдар қолданудың дамуына әсер етті. Сандардың жоғары шекарасы біртіндеп кеңейе келіп, натурал сандар қатары түзіледі. Біртіндеп келе натурал сандардың әрқайсысын белгілі бір жүйемен атау, таңбалау күн тәртібіне қойылды. Міне, осылай түрліше санау жүйесі немесе нөмірлеу қалыптасты. Сонау жүйелерінің ішіндегі тарихи жағынан ең алғашқысы және ең қарапайымы-екілік жүйе. Қазір жаппай қолданылып жүрген санаудың позициялық ондық жүйесі, яғни он цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, арқылы кез келген сандар сандық өрнек жүйесі бізге көне үнді жұртынан мирас болып қалған.

Сан ұғымының қалыптасуымен қатар сандарға төрт амал қолдану әрекеті туып жетілді. Сан ұғымы ендігі жерде бөлшек сан түрінде дамыды. Бөлшектер бүтін оң сандар сияқты күнделікті тұрмыс қажеттілігінен шыққан. Еүрліше ұзындық, аудан, көлем, уақыт тағы басқа сондай шамаларды өлшеу барысында олар есептеу практикасында қолданыс тапты.

Қорыта келгенде, арифметиканың бастапқы да негізгі ұғымдары мен әдістері тікелей өмір талабынан туындаған.

Теріс сандар, иррационал сандар, комплекс және гиперкомплекс сандар ұғымдарының шығуы сан ұғымының дамуының заңды жалғасы іспетті. Алайда бұл сандарды математиканың ішкі даму талабы туғызды, ал олардың ақылға қонымдылығы іс жүзінде сыналып айқындалды.

Геометрия ғылымының негізгі ұғымы болып саналатын фигуралар ұғымдарының қалыптасуы да арифметика негіздерінің шығу төркініне ұқсас. Геометрия грекше «гео»-жер және «метрейн»-өлшеу деген екі сөзден құралған. Осы атаудың өзінен-ақ геометрияның шығу тегі бірден аңғарылады.

Геометрия да арифметика сияқты адамдардың табиғатпен үздіксіз қарым-қатынасы нәтижесінде пайда болған. Бұл бақылау саналы түрде жүрмеген және өте ұзаққа сщзылған. Тарихқа дейінгі алғашқы «геометрлер» біз сияқты заттың басқа қасиеттерін жасанды түрде бөліп алған дерексіз ұғымдарды қарастырған. Оларда геометриялық ұғым және сол ұғымға сәйкес келетін табиғат нәрсесі, обьектісі ылғи қосарлана алынады. Мысалы, ежелгі адамдар үшін нүктелер өте алыстағы жұлдыздар немесе өте кіші түйіршіктер; ал түзулер-жарық сәулесі немесе тартылған жіп немесе басқа бір түзу сипаттас нәрселер, жазықтықтар-көлдің айдыны, тақыр жер, тақтаның беті тағы басқа болып есептеледі. Тіпті бертінде қабылданған цилиндр (дөңгелектеу), трапеция (үстел), Сфера (доп) сияқты геометриялық атаулар тікелей практикадан, ал үшбұрыш, төртбұрыш, дөңгелек, симетрия ұғымдарының да табиғаттың өзінен алынғаны даусыз.

Сан қилы өлшеу қажеттігінен ұзындық, аудан, көлем сияқты геометриялық шамалар жөніндегі ұғымдар қалыптасты. Адамдар бірте-бірте кейбір қарапайым геометриялық заңдылықтарды ашатындай дәрежеге көтерілді. Жер жыртушы диқан ұрпақтан-ұрпаққа көшкен тәжірибе жиынтығынан бөлінген жердің азды-көптігі қандай шамаларға байланысты екенін пайымдауға тиісті болды. Қисық жолға қарағанда түзу жолдың төте екенін аңғарту қтынға түспесе керек. Осылайша алғашқы геометриялық «теоремалар» дүниеге келді. Бірақ бұларды ешкім дәлелдемеді, дәлелдеуді керек те етпеді, өйткені бұл «теоремалардың» астарында күн сайын тұрмыста сан рет сыналып, шүбә келтірмейтін шындық жатты.

Уақытты өлшеу, түнде бағытты бағдарлау тәрізді әрекеттер аспан шырақтарының қозғалысын жүйелі түрде бақылап отыруды қажет етті. Бұл әрекет бұрыштарды өлшеудің, аспан сферасында орын алатын сандық қатынастарды, фтгураларды зерттеп білудің бастамасы еді. Энгельстің сөзімен айтқанда «Барлық басқа ғылымдар сияқты математика да адамдардың практикалық мұқтаждықтарынан, жер учаскелерінің ауданы мен ыдыстардың сыйымдылығын өлшеуден, уақытты есептеуден және механикадан шықты». «Сан және фигура ұғымдары, -деп жазды Энгельс өзінің «Анти-Дюринг» атты философиялық еңбегінде, -басқа ешқайдан емес, тек шындық дүниеден алынған. Адамдардың санауға үйренген, яғни алғашқы арифметикалық есепті шығаруға үйренген он саусағын не десеңіз о деңіз, тек әйтеуір ол ақыл-ойдың еркін шығармашылық жемісі емес. Санау үшін саналуға тиісті нәрселердің болуы ғана емес, сонымен бірге бұл нәрселерге көз жібергенде, олардың санынан басқа қасиеттеріне алаңдамайтын қабілет те болуы керек; ал ол қабілет тәжірибеге сүйенген ұзақ тарихи дамудың нәтижесі».

Математиканың бастапқы мағлұматтары азды-көпті барлық халықта болды деп айтуға болады.

Мәселен, көне түркі халықтарында (бұған қазақтар да кіреді) біздің заманымыздың бас кезінде кемел санау жүйесі болғаннан көрсететін жазба ескерткіштер бар (мысалы, Күлтегін ескерткіштеріндегі жазбалар) . Мұнда Ай, Күн және басқа аспан шырақтарының аты аталып, 100 мыңға дейін сан келтірілген. Қазақтың жұмбақ есептерінде көптеген терең математикалық астарлар жатыр. Мәселен, бір саулығым он жылда қанша бас қой болады деген есеп геометриялық прогрессияға келеді .

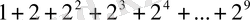Ал «Тоғыз құмалақ» ойыны тұнып тұрған математикалық талдаулар екені айқындалып отыр. Оның негізі - комбинаторикалық есептеулерде жатыр.

ІІ. ЭЙЛЕРДІҢ ЗАМАНЫ

ІІ. 1. XVIII ғасырдың көрнекті математиктері

XVIII ғасырдағы математиктердің бүкіл іс-әрекеттері анализ және оның механикаға қолданылысы төңірегінде шоғырланады. Ең күшті тұлғаларды олардың шығу тегі емес, интеллектуалдық тектестігін көрсететін шежіреге орналастыруға болады.

Лейбниц (1646-1716), Эйлер (1707-1783), Лагранж (1736-1813), Лаплас (1749-1827) . Бұл ғалымдардың еңбектерімен ағарту дәуірінің философтарымен қарым-қатынаста болған Клеро, Даламбар және Мепертюн бастаған француз математиктер тобының іс-әрекеттері тығыз байланысты. Бұларға швейцар математиктері Ламбертті және Даниил Бернуллиді қосу керек. Ғылыми жұмыстар негізінен академиаларда шоғырланды, бұлардың ішінде Париж, Берлин, Петербург академиялары көрнекті орын алды. Бұл кезде университеттерде мардымды сабақ өтпеді. Европаның алдыңғы қатардағы елерін оқымысты деспоттар билеп тұрды. Атақ - даңққа ие болуды мақсат еткен қатыгез әміршілер өздерінің маңына оқымыстыларды топтастырды. Мұның өзі қарулы күштердің жаугершілік қабілетін күшейтуге жаратылыстану мен қолданбалы математиканың маңызын түсінуге келіп тірелді. Мысалы, француз флотында аса жоғары сапалы (фрегаттар мен линкорларды жасауда) кеме жасаушылар үшін белгілі бір дәрежеде математикалық теорияны пайдаланған Эйлердің еңбектерінде армия мен флот үшін аса қажетті математикалық қолданыстар өте көп болған.

Швейцариядағы империялық еркін қала - Базель 1263 жылы әуел бастан ғылымның шоғырланған жері болды. Сонау Эразм аманының өзенде - ақ университеті бар маңызды орталық болған. Базельде және Голландияның басқа қалаларында көпес жақсылары билігімен ғылым мен өнер өркен жаяды. Базельдік ақсүйектерінің бір ғасыр бұрын испандықтар жаулап алған Антверпеннен бас сауғалап қашып келген Бернулли көпес семьясы да бар еді. Он жетінші ғасырдың соңынан қазірге дейін ағайынды Якоб пен Иоганн Бернуллиден тараған еді. Бұл әулеттің әрбір ұрпағынан оқымыстылар шығып келеді. Бастапқыда Якоб дін ғылымын Иоганн медицинаны қуады, алайда "Acta Eruditarum" журналында Лейбниц мақалаларымен кейін екеуі де біржола математик болуға бел байлады. Екеуі Лейбництің тұңғыш көрнекті шәкірттері болады.

1687 Якоб Базель университетінің математика кафедрасын алады. Мұнда ол 1705 жылы қайтыс болғанға дейін сабақ береді. Иогани 1697 ж. Голландианың Гронинг қаласына профессор болады, кейін ағасы өлгеннен соң Базельге келіп оның орнын басады, бұл қызыметті ол аттай қырық үш жыл атқарады. Якоб Лейбницпен 1687 жылдан бастап хат жазысып тұрады. Ол Лейбницпен үнемі пікір алысып, кейде бір - бірімен қатаң бәсекелестіккеде барады. Ағайынды екеуі де Лейбниц еңбектеріндегі бар асылдың қадыр - қасиетін ерте түсініп, ол қазынаны өз беттерінше аша түсуге ұмтылды. Олардың зерттеулерінде қазіргі дифференциалдық және интегралдық есептеудің элементар оқулықтарында бар көп нәрселерден басқа, бірсыпыра жай дифференциалдық теңдеулерді интегралдау келтірілген. Якоб полярлық координаталарды пайдаланады. Бұрын Гюйгенс және басқалар қарастырған тізбекті сызықтарды - лемнискатаны (1694) және логарифмдік спиральды зерттейді.

1690 жылы Лейбниц бойымен дене тұрақты жылдамдықпен түсетін қисық ретінде анықталған изохраниканы ашады, оның жартылай кубты парабола болатынын дәлелдейді, Якоб сонымен қатар, изопериметрлік фигураларды зерттеп вариациалық есептеу мәселелерін қолға алады. Әр түрлі түрленулерде қайта жаңғырып отыратын қасиеті бар логарифмдік спиральды (оның эвалютасы да логарифмдік спираль болады) тапқанда Якоб бұл қисықты өлгенде құлпытасына "өзгеріп барып, қайтадан осылай туамын" деп жазуды өсиет етіп қалдырған екен.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.