Үшбұрыштар

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Үшбұрыштар

Бір түзуде жатпайтын үш нүктеден және осы нүктелерді жұп-жұптан қосатын үш кесіндіден тұратын фигураны үшбүрыш деп атайды. Нүктелер - үшбұрыштың төбелері, ал

кесінділер - оның қабырғалары деп аталады. Үшбұрышты оның төбелеріне сәйкес келетін әріптер арқылы жазады және оны көбінесе Д символымен белгілейді.

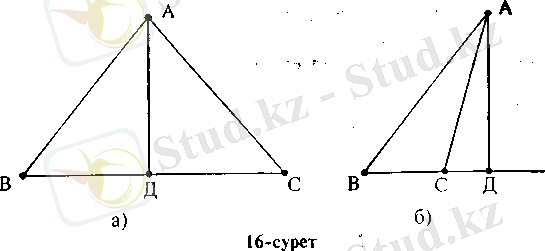
Үшбұрыштың берілген төбесінен жүргізілген биіктігі деп, осы тебеден қарама-қарсы қабырға жатқан түзуге жүргізілген перпендикулярды айтады. 16 а-суретте АД кесіндісі сүйір бұрышты АВС-ныңбиіктігі, ал 166-суретте АД кесіндісі доғал бұрышты АВС - ның биіктігі. Үшбұрыштың үш биіктігі ортоцентр деп аталатын бір нүктеде қиылысады. Үшбұрыштың а, в, с қабырғаларына түсірілген биіктіктері сәйкес һ _а , һ _ь , һ _с арқылы белгіленеді және келесі формулалармен есептеледі

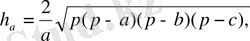
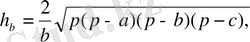
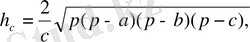
мұндағы 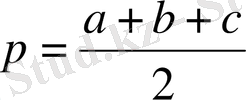- үшбұрыштың жарты периметрі.

Үшбұрыштың биссектрисасы деп, үшбұрыштың бұрышының биссектрисасының, бұрыштың төбесі мен оған қарама-қарсы жатқан қабырғасын қосатын кесіндісін айтады (17-сурет) . Үшбұрыштың барлық үш биссектрисасы бір нүктеде қиылысады және ол нүкте - іштей сызылған шеңбердің центрі.

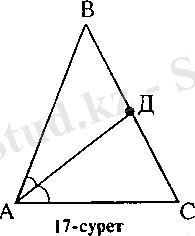
Үшбұрыштың а, в, с қабырғаларына жүргізілген биссектриссалары сәйкес l _a, l _b, l _c арқылы белгіленеді және келесі формулалармен есептеледі

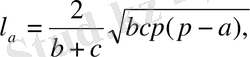
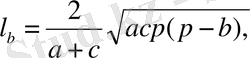
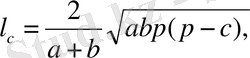
М9ндағы 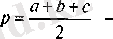үшбұрыштың жарты периметрі.

Үшбұрыштың ішкі бұрышының биссектрисасы қарсы жатқан қабырғаны үшбұрыштың қалған екі қабырғасына пропорционал болатын бөліктерге бөледі.

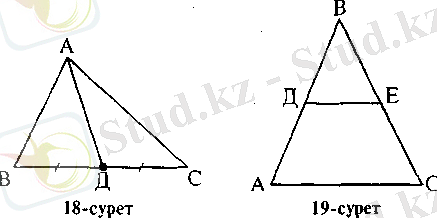
Үшбұрыштың берілген төбесінен жүргізілген медианасы деп, осы төбені қарама-қарсы жатқан қабырғаның ортасымен қосатын кесіндіні айтады (лат. medianus-орта) (18-сурет) .

Үшбұрыштың а, в, с қабырғаларына жүргізілген медианалары сәйкес т _а , т _ь , т _с арқылы белгіленеді және келесі формулалармен есептеледі

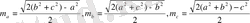
Медианалардың квадраттарының қосындысы үшбұрыштың қабырғаларының квадраттарының қосындысының төрттен үшіне тең

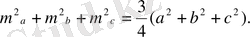
Тік бұрышты үшбұрыштың гипотенузасына түсірілген медиана, гипотенузаның жартысына тең.

Үшбұрыштың орта сызығы деп, оның екі қабырғасының орталарын қосатын кесіндіні айтады (19-сурет) . Орта сызық үшінші қабырғаға параллель және оның жартысына тең.

6-теорема. Кез келген үшбұрыштың әрбір қабырғасы басқа екі қабырғаларының қосындысынан кіші.

Екі кесіндінің ұзындықтары бірдей болса, оларды тең кесінділер деп атайды. Екі бұрыштың градустық бұрыш өлшемдері бірдей болса, оларды тең бұрыштар деп атайды.

Егер ABC мен А ₁ В ₁ С ₁ беріліп:

болса, онда АВС мен A _l B _l C _l meң үшбұрыштар деп аталады. Мұны қысқаша былай айтады: егер үшбұрыштардың сәйкес қабырғалары және сәйкес бұрыштары тең болса, ол үшбұрыштар тең.

Үшбұрыштардың тендігінің үш белгісі

7а теорема, ( үшбұрыштардың екі қабырғалары мен олардың арасындағы бұрышы бойынша теңдігінің белгісі) . Егер бір үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы басқа үшбұрыштың сәйкес екі қабырғасы мен олардың араларындағы бұрышқа тең болса, онда мұндай үшбұрыштар тең болады.

76 теорема, (үшбұрыштардың бір қабырғасы мен оған іргелес екі бұрышы бойынша теңдігінің белгісі) . Егер бір үшбұрыштың қабырғасы және оған іргелес екі бұрышы басқа үшбұрыштың сәйкес қабырғасы мен оған іргелес екі бұрышына тең болса, онда ондай үшбұрыштар тең болады.

7в теорема, ( үшбұрыштардың үш қабырғалары бойынша теңдігінің белгісі) . Егер бір үшбұрыштың үш қабырғалары екінші үшбұрыштың сәйкес үш қабырғаларына тең болса, онда ондай үшбұрыштар тең болады.

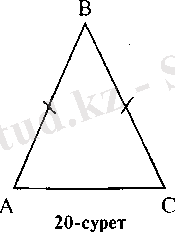Егер үшбұрыштың екі қабырғасы өзара тең болса, онда үшбұрыш тең бүйірлі деп аталады. Осы тең қабырғаларын үшбұрыштың бүйір қабырғалары, ал үшінші қабырғасы үшбұрыштың табаны деп аталады. 20-суретте: АВ = СВ, сондықтан АВС табаны- АС болатын тең бүйірлі үшбұрыш.

Буындары өзара қиылыспайтын сынықты жай сынық дейді.

Егер сынықтың шеттері беттессе оны тұйық сынық дейді

Сынықтың ұзындығы деп, оның буындарының ұзындықтарының қосындысын айтады.

1-теорема. Сынықтың ұзындығы оның шеттерін қосатын кесіндіден қысқа емес.

Дөңес көпбұрыштар

Көрші буындары бір түзуде жатпайтын түйық сынықты көпбұрыш деп атайды.

Сынықтың төбелері көпбұрыштың да төбелері, ал сынықтың буындары - көпбұрыштың қ абырғалары деп аталады.

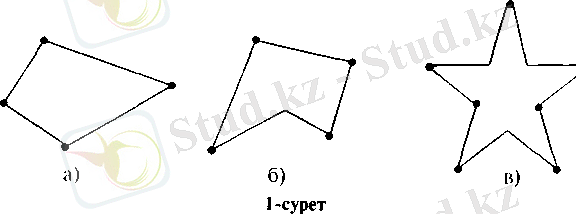
Көпбұрыштың көрші емес төбелерін қосатын кесінділер диагоналдар деп аталады. п төбелері бар, олай болса, п қабырғалары бар көпбұрыштарды п-бұрыш деп атайды. 1-суретте түрлі көпбұрыштар көрсетілген.

Жазық көпбұрыш немесе көпбұрышты аймақ деп, көпбұрышпен шектелген жазықтыктың ақырлы бөлігін айтады.

Көпбұрыштың кез-келген қабырғасы арқылы өтетін түзуге қарағанда бір жарты жазықтықта жататын көпбұрыш дөңес

деп аталады. 2а-суретте дөңес, ал 2б-суретте дөңес емес көпбұрыш бейнеленген.

2-теорема. Дөңес п бұрыштың бұрыштарының қосындысы 180" (н-2) тең.

Дұрыс көпбұрыштар

Дөңес көпбұрыштардың барлық қабырғалары және бұрыштары тең болса, оны дұрыс деп атайды. 3-суретте дұрыс көпбұрыштар: үшбұрыш, төртбұрыш (квадрат), бес-бұрыш және алтыбұрыш бейнеленген.

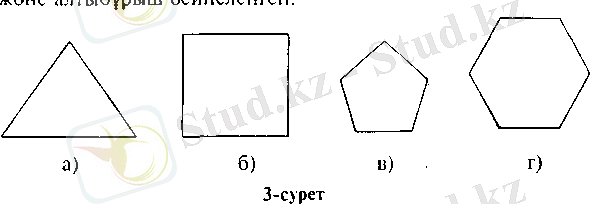
Егер көпбұрыштың барлық төбелері қандай да бір шеңбердің бойында жатса, оны шеңберге іштей сызылған көпбұрыш деп атайды. Егер көпбұрыштың барлық қабырғалары қандай да бір шеңберге жанасса, оны шеңберге сырттай сызылған көпбұрыш деп атайды.

Қабырғасы а тең п бұрышты дұрыс көпбұрышқа сырттай немесе іштей сызылған шеңбердің радиусы сәйкес келесі формула бойынша табылады

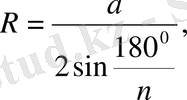
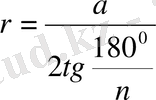
Дербес жағдайлар:

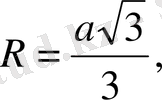
n=3, яғни дұрыс үшбұрыш үшін: п= 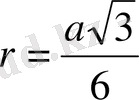4, яғни дұрыс төртбұрыш (квадрат) үшін:

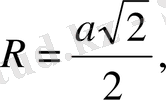
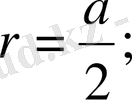
n = 6, яғни дұрыс алтыбұрыш үшін: R = a.

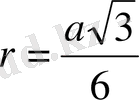
Үшбұрыштардың және көпбұрыштардын ұқсастықтары

Егер берілген екі үшбұрыштың бірінің бұрыштары екіншісінің сәйкес бұрыштарына тең болса, онда тең бұрыштарға қарсы жатқан қабырғаларды ұйқас деп атайды.

Сәйкес бұрыштары тең және ұйқас қабырғалары пропорционал үшбұрыштарды ұқсас деп атайды.

Үшбұрыштардың ұқсастық белгілері:

1. Үшбұрыштың екі бұрышы, екінші үшбұрыштың сәйкес бұрыштарына тен, болса, онда ол екі үшбұрыш ұқсас;

2. Үшбұрыштың екі қабырғасы екінші үшбұрыштың екі қабырғасына сәйкес пропорционал және осы қабырғаларының арасындағы бұрыштары тең болса, онда ол екі үшбұрыш ұқсас;

3. Үшбұрыштың үш қабырғасы екінші үшбұрыштың үш қабырғасына сәйкес пропорционал болса, онда ол екі үшбұрыш ұқсас.

Бір үшбұрыштың қабырғалары екінші үшбұрыштың қабырғаларына сәйкес параллель немесе перпендикуляр болса - олар ұқсас.

Үшбұрыштың қабырғасына параллель және оның басқа екі қабырғасымен қиылысатын түзу-осы үшбұрышка ұқсас үшбұрыш қияды.

Ұқсас үшбұрыштардың ұйқас қабырғаларына жүргізілген биіктіктері ұйқас биіктіктер деп аталады.

Ұйқас медианалар мен ұйқас биссектрисалар да осылай анықталады.

Көпбұрыштардың ұқсастықтары. Сәйкес бұрыштары тең және ұйқас қабырғалары пропорционал көпбұрыштар ұқсас деп аталады.

Шеңбер ұзындығы

3-теорема. Шеңбердің ұзындығының оның диаметріне қатынасы шеңберге байланысты емес, тұрақты 3, 1416 санына тең, яғни:

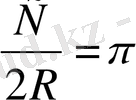(мұндағы С шеңбер ұзындығы) .

Бұдан, шеңбер ұзындығының формуласын аламыз: С = 2 R.

Шеңбердің екі радиусы арқылы күрылған бұрыш центрлік

Шеңбердің екі радиусы арқылы құрылған бұрыш центірлік деп аталды.

Центрлік бұрыш - өзінің тірелетін доғасының шамасына тең.

n ⁰ центрлік бұрышқа сәйкес келетін шеңбер доғасының ұ зындығы келесі формула бойынша есептеледі:

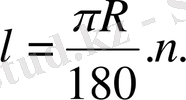
Бұрыштың радиандық өлшемі деп, оған сәйкес доға ұзындығының шеңбар радиусіне қатынасын айтады. Шеңбер доғасының ұзындығының формуласынан, бұрыштың п радиандық өлшемі градустық өлшемді -қа көбейткенге тең екендігі шығады: дербес жағдайда, 180" тең бұрыштың радиандық өлшемі л-ге тең, тік бұрыштың радиандық өлшемі - ге тең.

Бұрыштардың радиандық өлшем бірлігі - радиан. Бір радианға тең бұрыш доғасының ұзындығы радиуске тең болатын центрлік бұрыш.

180° Бір радианға тең бұрыштың градустық өлшемі

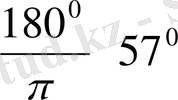
тең. Шеңбердің бір нүктесінен шығатын екі хордадан жасалған бұрыш- іштей сызылған бұрыш деп аталады. Іштей сызылған бұрыш оның тірелетін доғасының жартысына тең. Диаметрге тірелетін іштей сызылған бұрыш - тік.

Бір нүктеден шығатын екі жанамадан жасалган бұрыш - сырттай сызылған бұрыш деп аталады. Сырттай сызылған бұрыш - жанасу нүктелерінің арасындағы үлкен және кіші доғалардың айырымының жартысына тең.

Косинустар мен синустар теоремалары

4-теорема. (косинустар теоремасы) . Үшбұрыштың кез келген қабырғасының квадраты былайғы екі қабырғаларының квадраттарының қосындысынан, осы қабырғалар мен олардың арасындағы бұрыштың косинусының екі еселенген көбейтіндісін шегергенге тең (4-сурет) :

ВС ² = АВ ² + AC ² -2АВ- ACcosa.

Үшбұрыштың ауданын табуға келесі формулалар да қолданылады:

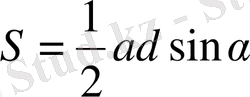
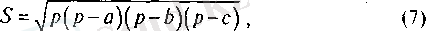а мен b - үшбұрыш қабырғалары, а - осы қабырғалар арасындағы бұрыш; Герон формуласы:

мұндағы а, Ь, с - үшбұрыш қабырғалары, р - оның жарты периметрі, яғни,

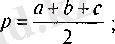
S = pr, (8)

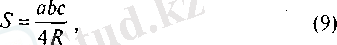мұндағы r - іштей сызылған шеңбер радиусі;

мұндағы R - сырттай сызылған шеңбер радиусі

Трапеция ауданы - оның табандарының жарым қосындысы мен биіктігі көбейтіндісіне тең, яғни,

мұндағы а мен b - трапеция табандары, Һ - биіктігі.

дөңгелектің ауданы келесі формула бойынша есептеледі:

R - дөңгелек радиусы.

Дөңгелектік сектор деп - орталық бұрыштың ішінде жатқан дөңгелек бөлігін айтады (1-сурет) : Дөңгелек секторының ауданы

(12)

формуласымен есептеледі. Мұндағы R - дөңгелек радиусы, а - сәйкес орталық бұрыштың градустық өлшемі.

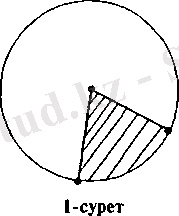
Дәңгелектің сегменті деп - дөңгелек пен шекарасы осы дөңгелектің хордасы

арқылы өтетін жарты жазықтықтың ортақ бөлігін айтады (2-сурет) :

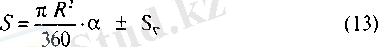Дөңгелектің сегментінің ауданы келесі формуламен есептеледі:

Мұндағы R - дөңгелек радиусы, а - дөңгелек сегментінің доғасына тірелген орталық бұрыштың градустық өлшемі, ал S төбелері - дөңгелек ортасы мен сәйкес секторды шектеп тұрған радиустердің шеттерінде болатын үшбұрыш ауданы. Erep a > 180" болса „+" таңба (2а-сурет), ал а < 180° болсау „-" (2б-сурет) таңба алынады.

КЕҢІСТІКТЕГІ ТҮЗУЛЕР МЕН ЖАЗЫҚТЫҚТАР

Түзулер мен жазықтықтардың параллелдігі

Бір жазықтықта жатпайтын және қиылыспайтын түзулерді айқас түзулер деп атайды. Айқас түзулер арасындағы бұрыш деп оларға параллель қиылысатын түзулер арасындағы бұрышты айтады.

Екі айқас түзулерге ортақ перпендикуляр деп олардың әрқайсысына перпендикуляр, шеттері осы түзулерде болатын кесіндіні айтады.

Айқас түзулер арасындағы қашықтық деп оларға ортақ перпендикулярдың ұзындығын айтады. Ол осы түзулер арқылы өтетін жазықтықтардың ара қашықтығына тең болады.

Қиылыспайтын түзу мен жазықтықты параллель деп айтады. а түзуінің а жазықтығына параллельдігін а // а деп жазады.

1-теорема (түзу мен жазықтықтың параллельдік белгісі) . Егер жазықтықта жатпайтын түзу осы жазықтықтағы қандай да бір түзуге параллель болса, онда ол жазықтыққа да параллель болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.