Пікірлер және предикаттар

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Пікірлер және предикаттар

Жоспар

Пікірлер
Күрделі пікірлер
Пікірлерді теріске шығару
Пікірлер конъюнкциясы
Пікірлер дизъюнкциясы
Предикаттарды терістеу, олардың конъюнкциясы және дизъюнкциясы

Пікірлер

Бірқатар жәй хабарлы сөйлемдерді қарастырайық:

Қазақстан - егеменді мемлекет;
Натурал сандар жиыны ақырсыз;
25 саны 5-ке еселі;
Құр жиынның элементі бар;
38 саны 3-ке бөлінеді.

Бұл сөйлемдердің барлығы мазмұны жағынан әртүрлі. Бірақ олардың барлығына ортақ бір қасиеттің бар екенін байқауға болады. Осы ортақ қасиет - кейбір сөйлемдерде ақиқат (дұрыс, дәл), ал басқаларында жалған (дұрыс емес, қате) ойлардың айтылуы. 1, 2, 3 сөйлемдерді ақиқат, ал 4, 5 сөйлемдер жалған деп есептейміз.

Хабарлы сөйлемнің ақиқат немесе жалған екендігін айтуға болса, онда ол пікір деп аталады.

Математикада пікірлермен үнемі кездесіп отырамыз және ондай пікірлерді жазу үшін >, <, =, ≠ т. б. символдарды пайдаланамыз. Мысалы, «12 > 7» пікірі «12 саны 7-ден артық» деген сөйлемнің математикалық жазылуы болып табылады.

Кез келген хабарлы сөйлем пікір болмайтынын көрсетейік. Мысалы, «х > 7», «х+4= 8», «х+е-37=0» сөйлемдері пікір бола алмайды, өйткені сөйлемдердегі айнымалылардың мәндері белгісіз болғандықтан олардың әрқайсысының ақиқат немесе жалған екендігі туралы айта аламыз. Қандай да бір сөйлем туралы ол ақиқат немесе жалған деп үнемі айта аламыз. Пікірлерді латын алфавитінің үлкен әрпімен, ал олардың мағынасы ақиқат болса, «а» әрпімен, жалған болса «ж» әрпімен белгілеу келісілген.

Ескерту: Кейбір оқулықтарда ақиқат және жалған деген сөздерді сәйкесінше 1 және 0 цифраларымен белгілейді.

Бастауыш мектеп оқушылары математика пәнінің алғашқы сабағынан бастап ақиқат пікірмен кездеседі. Олар 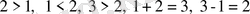т. с. с. пікірлермен танысады. Одан кейін екі таңбалы, үш таңбалы сандар туралы пікірлер, күрделі сандық өрнектердің теңдігі, теңсіздігі туралы пікірлерге кездесетін болады. Мысалы, «мына амалдардың дұрыс орындалғандығын не дұрыс орындалмағандығын текксеріңіздер»:

517 + 408 = 925

804 - 235 = 579

Басқаша айтқанда, бұл жаттығуда берілген теңдіктердің ақиқат немесе жалған екендіктерін анықтау талап етіледі. Есептеу арқылы оқушы бірінші теңдіктің ақиқат, ал екінші теңдіктің жалған екендігіне көз жеткізеді.

Басқа жаттығуларда:

12 - 5 > 3
18 + 24 < 30
25 · 41 ≠ 25 · 40
9145 - 7583 = 1544 + 1234
5009 - 324 < 4395 т. с. с.

жазуларының дұрыс немесе дұрыс емес екендігін анқтау талап етіледі.

Мұндай жаттығуларды орындауда пікір ұғымын пайдаланып отырамыз, өйткені берілген сөйлемдердің ақиқат немесе жалған екендігін анықтау талап етіліп отыр.

Күрделі пікірлер

Пікірлер элементар (жәй) және күрделі (құрама) болып келеді.

Элементар пікір деп оны басқа пікірлерге жіктеуге келмейтін пікірді айтамыз.

Егер пікірді бірнеше элементар пікірге жіктеуге болса, онда оны күрделі пікір деп атайды.

Күрделі пікір әртүрлі жалғаулықтар және сөз тіркестері арқылы элементар пікірлерден құрылады. Мысалы, «102 саны жұп және 9-ға бөлінеді», «3 < 6 < 7», «берілген төртбұрыш - ромб немесе квадрат» деген пікірлердің әрқайсысы күрделі. Олар элементар пікірлерді «және», «немесе» деген сөздермен байланыстыру арқылы алынып тұр.

Күрделі пікірлерді «егер», «онда», «сонда тек сонда ғана» деген сөздерді пайдаланып та алуға болады. Мысалы, «Егер ұшбұрыштың екі қабырғасы тең болса, онда ол теңбүйірлі», «трапеция теңбүйірлі болса, сонда тек сонда ғана оны сырттай шеңбер сызуға болады».

Грамматикада «және», «немесе», «егер», «онда», «сонда тек сонда ғана» сөздерін жалғаулық деп атайды. логикада оларды элементар пікірлер арасындағы байламдар деп атайды, өйткені мұндай жалғаулықтар элементар пікірлерді бір күрделі пікірге біріктіреді.

Сөйлем құрылысында қолданылатын «емес» сөзі мен «дұрыс емес» деген тіркесті қарастырайық. Аталған тіркес қандай да бір пікірді теріске шығару мақсатында қолданылады: Мысалы, «12 жәй сан». Бұл жалған пікір, себебі 12 саны 1 мен өзінің басқа да сандарға бөлінеді. Осы сөйлемге «емес», «дұрыс емес» сөздерін қолданайық. Сонда, «12 жәй сан емес», «12 жәй сан деген дұрыс емес» деген сөйлемдер құрастырамыз. Ал, бұл пікірлер ақиқат болады.

Сонымен, «және», «немесе», «егер, онда», «сонда тек сонда ғана», «емес», «дұрыс емес», т. б. байламдар арқылы кез-келген элементар пікірлерден әртүрлі күрделі пікірлер алуға болады және олардың мағыналық сипатына көңіл аударылмайды. Пікірлер теориясында күрделі пікірге кіретін элементар пікірлердің ақиқат немесе жалған екендігіне байланысты күрделі пікірдің де ақиқат немесе эалған екендігі зерттеледі.

Пікірді теріске шығару

Кез келген А пікірінен, оны теріске шығара отырып, яғни А пікірі орындалмайды деп қабылдап, жаңа пікір алуға болады.

А пікірін теріске шығаруды 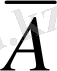деп белгілейді, ол «А емес» деп оқылады, мысалы, егер А - «Тік төртбұрыштың диагональдары тең» деген пікір болса, онда 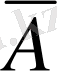- «Тік төртбұрыштың диагональдары тең емес» деген пікір болады. Бұл мысалда А пікірі ақиқат, ал 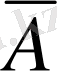пікірі жалған.

Егер А - «128 саны жәй сан» десек, 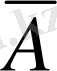- «128 саны жай сан емес» деген пікірді білдіреді. Бұнда керісінше, А - пікірі жалған, ал 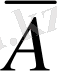- ақиқат пікір.

Сонымен, А қандай пікір болғанымен, А және 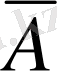екі пікірінің бірі - ақиқат, екіншісі - жалған болады.

А және 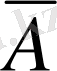арасындағы байланысты кесте арқылы көрсетуге болады. Мұндағы «а» әрпі ақиқат. «ж» әрпі жалған дегенді белгілейді. Осы түрдегі кестені ақиқаттық кесте деп атайды.

А: а

а: ж

А: ж

а: а

А қандай да бір пікір болсын. Сонда оның теріс пікірі 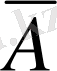-да пікір болып табылады, ендеше 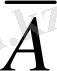пікірінің де, теріс 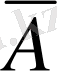пікірін қарастыруға болады. Оны А пікірін екі рет теріске шығару деп атайды. А пікірін екі рет теріске шығару, А пікірінің өзі екенін көрсету қиын емес. Оған 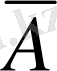пікірінің ақиқаттық кестесін құру арқылы көз жеткізуге болады. Басқаша айтқанда, кез келген пікірді екі рет теріске шығара отырып алғашқы пікірді аламыз, яғни 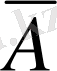=А.

А: а

: ж

: а

А: ж

: а

: ж

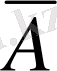
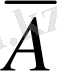
Егер айтылған пікірдегі баяндауышқа «емес» шылауын қоссақ, пікірдің теріске шығатыны көрдік. Ал егер А пікіріндегі баяндауыштың «емес» шылауы болса, онда 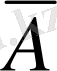пікірін құру үшін ол шылауды алып тастау керек.

Егер А - «бүгін күн суық емес» болса, 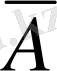- «бүгінгі күн суық» болады.

Пікірлер конъюнкциясы

Паралеллограмның мынандай қасиеттерін қарастырайық:

АД қабырғасы ВС қабырғасына паралелль және оған тең;
АВСД паралеллограмның диагональдары бір нүктеде қиылысады және қақ бөлінеді.

Осы мысалдағы күрделі пікірлердің әрқайсысы екі элементар пікірлерді «және» жалғаулығы арқылы біріктіруден шыққандығын көреміз.

Егер бірінші элементар пікірді А, екіншісін В әрпімен белгілесек, онда берілген сөйлемді «А және В» деп жазады, яғни әр түрлі мазмұндағы сөйлемдер логикалық бір ғана формада жазылады.

«А және В» деген пікірді А, В пікірлерінің конъюнкциясы деп атайды.

Анықтама: А мен В пікірлерінің екеуі де ақиқат болғанда ғана ақиқат болатын күрделі пікірді рсы пікірлердің конъюнкциясы деп атайды.

Егер А мен В пікірлерінің ең болмағанда біреуі жалған болса, онда олардың конъюнкциясы жалған болады. А, В пікірлерінің конъюнкциясын 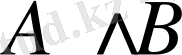түрінде белгілейді.

Жоғарыдағы анықтамадан 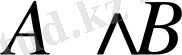конъюнкциясы үшін ақиқаттық кестесі мынандай болады:

А: а

В: а

: А

А: а

В: ж

: Ж

А: ж

В: а

: Ж

А: ж

В: ж

: Ж

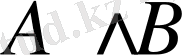
Мына «Күн Жерден үлкен» және «Астана - Қазақстанның астанасы» деген пікірді қарастырайық. Бұл пікір «Күн Жерден үлкен» және «Астана - Қазақстанның астанасы» деген пікірлердің конъюнкциясы болады. Сонымен қатар ол ақиқат пікір, өйткені оны құрайтын екі пікірдің екеуі де ақиқат.

«Күн Жерден үлкен» және «Ертіс Каспий теңізіне құяды» деген конъюнкция жалған, өйткені оған енетін элементар пікірлердің біреуі «Ертіс Капийге құяды» жалған.

«12 тақ сан және 5-ке бөлінеді» деген пікір жалған, себебі бұл конъюнкцияға кіретін екі элементар пікірдің екеуі де жалған.

Пікірлердің конъюнкциясы қос теңсіздіктерді қарастырғанда кездеседі. Мысалы, 3 < 7 <10 теңсіздігі “3 <7” және “7<10” деген екі пікірдің конъюнкциясы болады, яғни 3 < 7 <10 теңсіздігін “3 < 7 <10” түрінде жазуға болады, сонымен қатар бүл пікір ақиқат, өйткені оған енетін “3 <7”, “7<10” пікірлерінің әрқайсысы ақиқат.

“9 < 7 <10” деген теңсіздігі жалған, өйткені ол “9 <7” деген жалған және “7<10” деген ақиқат пікірлердің конъюнкциясы.

Жалпы сөйлемнің құрылуында «және» жалғаулығының орнына «ал», «бірақ», «алайда», «дегенмен», т. б. жалғаулықтарды қолданылады. Бұл жалғаулықтардың әртүрлі ерешеліктері болғанмен, логикалық көзқараста олардың айырмашылығы жоқ.

Теріске шығару және конъюнкция операциялары арқылы элементар пікірлерден 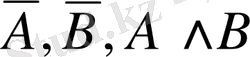түріндегі пікірлер ғана емес, одан да күрделі 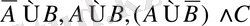т. с. с. пікірлерді құруға болады.

Мысалы:

А: «Әлішер - оқу озаты»;

В: «Әлішер тәртіпті»;

С: «Әлішер спортпен шұғылданады»;

Д: «Әлішер саяхат құруды жақсы көреді» деген пікірлер берілсін.

Осы элементар пікірлерден мынандай күрделі пікірлер құруға болады:

1) «Әлішер оқу озаты және саяхет құруды жақсы көреді»;

2) «Әлішер оқу озаты, тәртіпті және саяхат құруды жақсы көреді»;

3) «Әлішер саяхат құруды жақсы көреді, ал спортпен шұғылданбайды»;

4) «Әлішер спортпен щұғылданбайды және саяхат құруды жақсы көрметіні дұрыс емес».

Осы күрделі пікірлерді былайша өрнектеп жазуға болады:

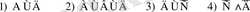
Сонымен, нақтылы күрделі пікірдегі элементар пікірлерді әріптермен алмастырып берілген күрделі пікірдің логикалық құрылымын анықтайтын өрнекті аламыз. Осындай өрнек бар болса, онда оның ақиқат немесе жалған екендігін, яғни осы өрнекке сәйкес келетін күрделі пікірдің ақиқат немесе жалған екендігін анықтауға болады.

Мұны ақиқаттық кесте арқылы орындау ыңғайлы. Мысалы, А мен В пікірлерінің барлық мүмкін мәндерінде 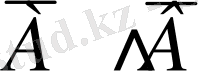өрнегінің мәнін табайық. Ақиқкт кесте былайша толтырылады: А мен В пікірлерінің барлық мүмкін мәндерін жазамыз (1, 2 - бағандар) сонан соң 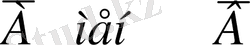мәнін тауып (3, 4 - бағандар) конъюнкцияның анықтамасы бойынша 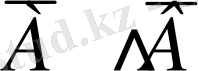мәнін 3, 4 бағандағы мәндердің конъюнкциясы арқылы анықтайды:

А: а

В: а

: ж

А: а

В: ж

: ж

: а

: ж

А: ж

В: а

: а

: ж

А: ж

В: ж

: а

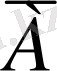
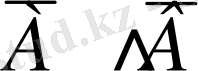
Пікірлер дизъюнкциясы

Мынандай мысалдарды қарастырайық:

«102 саны жұп немесе 3-ке бөлінеді»;
«Мен театр немесе қонаққа барамын»;
«Ол жұмысқа автобуспен немесе трамваймен келеді».

Бұл келтірілген пікірлер күрделі, олардың бәрінің формасы «А немесе В» түрінде болады. «А немесе В» формасындағы пікірді А мен В пікірлерінің дизъюнкциясы деп атайды.

Анықтама: А мен В пікірлерінің екеуі де жалған болғанда жалған болып, қалған жағдайдың бәрінде ақиқат болатын күрделі Амен В пікірлерінің дизъюнкциясы деп аталады.

А, В пікірлерінің дизъюнкциясы деп белгіленеді.