Орналастырулар мен терулер: қайталанатын және қайталанбайтын комбинацияларды санау әдістері


Комбинаторикалық үйлесімді кескіндерді (конфигурацияларды) қайта есептеу формулалары
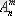 қайталанбайтын орналастырулардың саны көбейтіндінің ережесінің көмегімен анықталуы мүмкін. m элементтердің біріншісінің орналастырулары n тәсілмен алынуы мүмкін, екіншісі (n-1) тәсілмен. Онда бірінші алынған элемент қайталанбайтын болғандықтан, осыған ұқсас үшінші үшін (егер m>2) (n-2) тәсіл қалады, т. б.
қайталанбайтын орналастырулардың саны көбейтіндінің ережесінің көмегімен анықталуы мүмкін. m элементтердің біріншісінің орналастырулары n тәсілмен алынуы мүмкін, екіншісі (n-1) тәсілмен. Онда бірінші алынған элемент қайталанбайтын болғандықтан, осыған ұқсас үшінші үшін (егер m>2) (n-2) тәсіл қалады, т. б.
 Барлық m элементтерінің алынуы
Барлық m элементтерінің алынуы
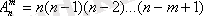 тәсілдерімен n-нен басталып 1-ге келіп отыратын көбейтінділерден тұрады. Басқаша
тәсілдерімен n-нен басталып 1-ге келіп отыратын көбейтінділерден тұрады. Басқаша
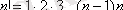 формуланы пайдаланып былай жазады
формуланы пайдаланып былай жазады

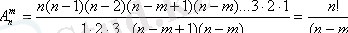
 Мысалы,
Мысалы,
 1)
1)
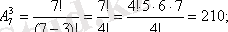

 2)
2)
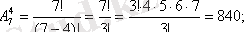
 3)
3)
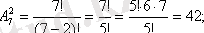
 4)
4)
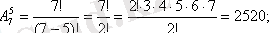
 Егер m=1, онда
Егер m=1, онда
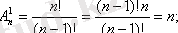
 Егер m=n-1, онда
Егер m=n-1, онда
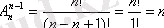
Мұнда 0!=1, 1!=1

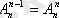 екі сандардың теңдігі табиғи: егер n элементтен (n-1) -і алынса, онда қалған бір элемент бір тәсілмен алынуы мүмкін және бұл
екі сандардың теңдігі табиғи: егер n элементтен (n-1) -і алынса, онда қалған бір элемент бір тәсілмен алынуы мүмкін және бұл
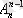 санын
санын
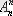 санымен салыстырғанда өзгеріссіз қалады. Сондықтан, n алмастыру Р
n
=n! (n, m) қайталанбалы орналастырулар - кортеждер, басқаша айтқанда n элементті алфавиттегі ұзындығы m-ге тең деген сөз. Көбейтінді ережесін қолдана отырып, қайталанбалы орналастырудың (n, m) әр түрлі саны
санымен салыстырғанда өзгеріссіз қалады. Сондықтан, n алмастыру Р
n
=n! (n, m) қайталанбалы орналастырулар - кортеждер, басқаша айтқанда n элементті алфавиттегі ұзындығы m-ге тең деген сөз. Көбейтінді ережесін қолдана отырып, қайталанбалы орналастырудың (n, m) әр түрлі саны
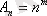
 екендігін оңай көрсетуге болады. Шынында, басқаларына байланысты емес әрбір n мүшелердің ретті тізбектен алынуы мүмкін, ал олардың саны m-ге тең болады. Мысалдар:
екендігін оңай көрсетуге болады. Шынында, басқаларына байланысты емес әрбір n мүшелердің ретті тізбектен алынуы мүмкін, ал олардың саны m-ге тең болады. Мысалдар:
 - {0, 1} алфавитіндегі m ұзындықты сөздердің саны 2
m
-ге тең m элементті барлық бөліктерінің саны осындай, сондықтан жиын бір мәнді характеристикалық функция арқылы беріледі. m-мәнді екілік сандардың саны 2
m-1
тең, себебі бірінші сан 1-ге тең болуы керек.
- {0, 1} алфавитіндегі m ұзындықты сөздердің саны 2
m
-ге тең m элементті барлық бөліктерінің саны осындай, сондықтан жиын бір мәнді характеристикалық функция арқылы беріледі. m-мәнді екілік сандардың саны 2
m-1
тең, себебі бірінші сан 1-ге тең болуы керек.
 - Қайталанбайтын терудің (n, m) саны
- Қайталанбайтын терудің (n, m) саны
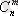 не
не
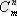 символымен белгіленеді де, оны биномдық коэффициенттер деп атайды, себебі х+у екі мүшесінің n дәрежесіндегі Ньютон биномы туралы коэффициенттеріне тең болады.
символымен белгіленеді де, оны биномдық коэффициенттер деп атайды, себебі х+у екі мүшесінің n дәрежесіндегі Ньютон биномы туралы коэффициенттеріне тең болады.

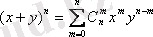 (1. 4. 1)
(1. 4. 1)
Шынында,
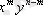 мүшесінің коэффициенті (х+у) (х+у) . . . (х+у), бірдей n көбейткіштердің х-тің алынуы m рет, у-тің алынуы (n-m) рет көбейткіштермен бірігіп
мүшесінің коэффициенті (х+у) (х+у) . . . (х+у), бірдей n көбейткіштердің х-тің алынуы m рет, у-тің алынуы (n-m) рет көбейткіштермен бірігіп
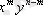 көбейтіндіге тең болады. (n, m) қайталанбайтын теруді қайта есептеу үшін (n, m) қайталанбайтын орналастырудың құрамы бірдей элементтер эквиваленттік класс қатынаста болуы тиіс, ал өзгешелігі бар элементтер құрамын теру әр түрлі класқа тиеді. Кластардың әрбіреуіне бірдей m әр түрлі элементтерден тұратын үйлесімді кескіндер кіреді, яғни олар m алмастыруды көрсетеді және әрбір класта олардың саныm!. Осыдан қайталанбайтын (n, m) терудің саны
көбейтіндіге тең болады. (n, m) қайталанбайтын теруді қайта есептеу үшін (n, m) қайталанбайтын орналастырудың құрамы бірдей элементтер эквиваленттік класс қатынаста болуы тиіс, ал өзгешелігі бар элементтер құрамын теру әр түрлі класқа тиеді. Кластардың әрбіреуіне бірдей m әр түрлі элементтерден тұратын үйлесімді кескіндер кіреді, яғни олар m алмастыруды көрсетеді және әрбір класта олардың саныm!. Осыдан қайталанбайтын (n, m) терудің саны
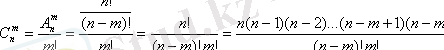
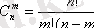 (1. 4. 2)
(1. 4. 2)
m-ның аз мәні үшін соңғы өрнекке
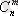 болуы қолайлы, себебі алымы да, бөлімі де m көбейткіштер алымында n-нен басталып бірге азайып отыратын натурал қатар, бөлімінде бірден басталып бірге отыратын натурал қатар [1, k] кездейсоқ түрі
болуы қолайлы, себебі алымы да, бөлімі де m көбейткіштер алымында n-нен басталып бірге азайып отыратын натурал қатар, бөлімінде бірден басталып бірге отыратын натурал қатар [1, k] кездейсоқ түрі
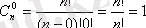 ,
,
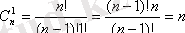 ,
,
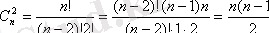
Егер m>n болса, онда
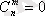 деген қолайлы.
деген қолайлы.
Мысалы:
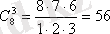 ,
,
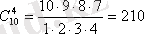 .
.
1. 5 Биномдық коэффициенттердің қасиеттері
Биномдық коэффициенттердің кейбір қасиеттерін келтірейік.
1)
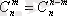 . Бұл (1. 4. 2) -формуладан шығады, себебі n элементтен m элемент алынуы бір мәнді толықтауышты анықтайды, яғни n элементтен (n-m) алынуы, қалған элементтің алынуын көрсетеді. Сондықтан бұрыңғы теңдіктерден мынау шығады:
. Бұл (1. 4. 2) -формуладан шығады, себебі n элементтен m элемент алынуы бір мәнді толықтауышты анықтайды, яғни n элементтен (n-m) алынуы, қалған элементтің алынуын көрсетеді. Сондықтан бұрыңғы теңдіктерден мынау шығады:
,
.
2)
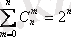 - бұл (1. 4. 1) -формула х=у=1 қойсақ, осы қасиет шығады. Мысалы,
- бұл (1. 4. 1) -формула х=у=1 қойсақ, осы қасиет шығады. Мысалы,
1+5+10+10+5+1=32=2 5 ,
1+6+15+20+15+6+1=64=2 6
3)
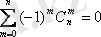 (1. 4. 1) -формулаға х=1, у=-1 қойсақ, осы шығады: мысалы, n=6 үшін:
(1. 4. 1) -формулаға х=1, у=-1 қойсақ, осы шығады: мысалы, n=6 үшін:
1-6+15-20+15-6+1=0
4)

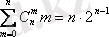
Теңдіктің дұрыстығын тексеруге n элементтен {а
1
, а
2
, . . . а
n
} алынған әрбір теру үшін жеке карточкаға
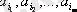 символдар жазылған сәйкес элементтерге осы m элементінің теруі көрсетіледі, екінші қасиет бойынша барлық карточкалар саны 2
n
болады. Сондықтан, барлық карточкалардағы символдардың қосындысын екі түрлі есептелуі мүмкін:
символдар жазылған сәйкес элементтерге осы m элементінің теруі көрсетіледі, екінші қасиет бойынша барлық карточкалар саны 2
n
болады. Сондықтан, барлық карточкалардағы символдардың қосындысын екі түрлі есептелуі мүмкін:
а) m символдарды ұстайтын
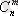 карточкасының саны
карточкасының саны
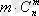 -ға тең; қарастырылған теңдіктің сол жағы барлық карточкалардағы символдардың жалпы саны үшін k=0, 1, …, n.
-ға тең; қарастырылған теңдіктің сол жағы барлық карточкалардағы символдардың жалпы саны үшін k=0, 1, …, n.
б) Егер барлық карточкалардағы жазылған кейбір
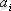 символын сызып тастасақ, онда олардың әр түрлі теруі қалған (n-1) элементтерінің саны 2
n-1
, демек
символын сызып тастасақ, онда олардың әр түрлі теруі қалған (n-1) элементтерінің саны 2
n-1
, демек
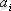 жазылған карточка 2
n-1
тең. Теңдіктің оң жағындағы символдардың жалпы саны n∙ 2
n-1
.
жазылған карточка 2
n-1
тең. Теңдіктің оң жағындағы символдардың жалпы саны n∙ 2
n-1
.
Мысалы, n=5 үшін: 0∙1+1∙5+2∙10+3∙10+4∙5+5∙1=80=5∙16=5∙2 4 .
n=6 үшін: 0∙1+1∙6+2∙15+3∙20+4∙15+5∙6+6∙1=192=6∙32=6∙2 5
5)
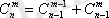
Теңдік мынадай пікірден шығады: n элементті жиынның кейбір х элементін жазып қоямыз. m элементті соңғы жиынның бөлігінің бәрі (олардың саны - теңдіктің сол жағы) екі қиылыспайтын кластарға бөлінеді: х элементін ұстайтын және ұстамайтын.
Бірінші класта
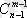 жиын бөліктері. Олар х-ті (n-1) элементтердің қалғандарынан (m-1) элементтерді ұстайды. Екінші класта
жиын бөліктері. Олар х-ті (n-1) элементтердің қалғандарынан (m-1) элементтерді ұстайды. Екінші класта
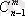 элементтердің болуы айқын. Соңғы тепе-теңдік (сурет 1) Паскаль үшбұрышы
1
деп аталатын схемамен байланысты.
элементтердің болуы айқын. Соңғы тепе-теңдік (сурет 1) Паскаль үшбұрышы
1
деп аталатын схемамен байланысты.
Егер үшбұрыштың жолдарын рет бойынша 0, 1, 2, . . . сандармен нөмірлесек, онда і-жолда
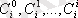 құратын сандар болады. 5-ші қасиет бойынша бірге тең. Шеткісінен басқа әрбір жолдағы сан тұрған сандардың қосындысы болуы мүмкін. Бұл Паскаль үшбұрышының жабайы (канондық) құрамын көрсетеді және одан берілген n-ші жолдағы бином (х+у)
n
коэффициенттерін оңай табуға болады.
құратын сандар болады. 5-ші қасиет бойынша бірге тең. Шеткісінен басқа әрбір жолдағы сан тұрған сандардың қосындысы болуы мүмкін. Бұл Паскаль үшбұрышының жабайы (канондық) құрамын көрсетеді және одан берілген n-ші жолдағы бином (х+у)
n
коэффициенттерін оңай табуға болады.
Ескерту. 5-ші қасиет рекуренттік қайталанбалы ара қатынас мысалын көрсетеді:
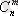 шамасы (n, m) екі аргументтен құралған функция ретінде қарастырылады да, басқа кіші мәндеріндей аргументтері де осы функцияның мәні арқылы өрнектеледі.
шамасы (n, m) екі аргументтен құралған функция ретінде қарастырылады да, басқа кіші мәндеріндей аргументтері де осы функцияның мәні арқылы өрнектеледі.
Сурет 1 Паскаль үшбұрышы
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
. . .
6)
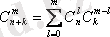 (Коши тепе-теңдігі)
(Коши тепе-теңдігі)
Дәлелдеу үшін мынадай түсініктемені қарастырған қолайлы. n еркектер және k әйелдерден құралған топтардан m адамды делегацияға алады. Ол
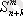 тәсілдерімен орындалуы мүмкін. (n+k) жиынының m-элементі жиынның бөліктерінің бәрін өрнектердің саны бойынша делегацияға m элементті делегацияны S еркектерді ұстайтын
тәсілдерімен орындалуы мүмкін. (n+k) жиынының m-элементі жиынның бөліктерінің бәрін өрнектердің саны бойынша делегацияға m элементті делегацияны S еркектерді ұстайтын
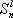 тәсілдермен S еркектер алынуы мүмкін, ал одан кейін m-s әйелдерді
тәсілдермен S еркектер алынуы мүмкін, ал одан кейін m-s әйелдерді
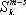 тәсілдердің бірі арқылы жүйеленуі мүмкін. Көбейтінді ережесі бойынша осындай делегациялардың саны
тәсілдердің бірі арқылы жүйеленуі мүмкін. Көбейтінді ережесі бойынша осындай делегациялардың саны
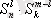 тең, ал қосынды ережесі бойынша m элементті делегациялардың осындай теңдіктің оң жағындағы сияқты.
тең, ал қосынды ережесі бойынша m элементті делегациялардың осындай теңдіктің оң жағындағы сияқты.
Мысалы,
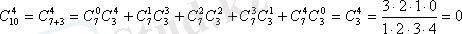
(
, себебі m=4, n=3 4>3)
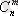 қайталанбалы терудің (n, m) санын алу үшін әрбір осындай теруге, яғни ретсіз n элементтік жиыннан m алынуын екі әріпті алфавиттегі {0, 1} кортеждің мынандай тәсілмен алынуын сәйкес қоямыз. Алдымен n натурал саны арқылы {a
i
} кортежін құрамыз да, і-ші элементтердің n-жиынынан m осы сұрыптауға кіретін санға тең а
і
болады.
қайталанбалы терудің (n, m) санын алу үшін әрбір осындай теруге, яғни ретсіз n элементтік жиыннан m алынуын екі әріпті алфавиттегі {0, 1} кортеждің мынандай тәсілмен алынуын сәйкес қоямыз. Алдымен n натурал саны арқылы {a
i
} кортежін құрамыз да, і-ші элементтердің n-жиынынан m осы сұрыптауға кіретін санға тең а
і
болады.
а
і
-дің кейбіреулері өзара тең болуы мүмкін, n компонентті осындай кортеждің қосындысы m-ге тең. Одан әрі ноль мен бірден кортеж құрамыз да, әрбір а
і
санын а
і
бірлігімен өзгертеміз, оларды нольдермен кезектестіреміз
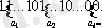 .
.
Егер кейбір а і =0, онда сәйкес нольдердің арасында ешқандай бірліктер болмайды. Басқаша айтқанда, кортеж (n-1) нольдерден n орынды анықтайды: барлық кортеждің сан жағына және әрбір нольдерден оңға қарай і-дің орнына а і бірлік қоямыз (а і -дің кейбіреулері бұрыңғы айтқан бойынша 0-ге тең) .
Мысалы, (4, 7) теруге (1, 1, 3, 4, 4, 4, 4) сәйкес (2, 0, 1, 4), ал оған кортеж 1100010111; (4, 7) теруге (1, 2, 2, 2, 3, 3, 3) сәйкес алдымен кортеж (1, 3, 3, 0), ал кейін кортеж 1011101110. Нәтижесі (n-1) нольдерден және m бірліктерден тұратын теруді аламыз, яғни вектордың ұзындығы (n+m-1) болады.
Керісінше, осындай әрбір векторға (n, m) теруі сәйкес келеді де, серия болып, біртіндеген тәртіппен келетін бірліктер а і санын анықтайды, олардың қосындысы m-ге тең. Сондықтан
(1. 4. 3)
(1. 4. 3) теңдікті басқаша жолмен алынуы мүмкін. (с 1 , с 2 , . . . , с m ) қайталанбалы (n, m) теруі болсын және де
Оған (d 1 , d 2 , …, d m ) бұл (n+m-1, m) қайталанбайтын теру берілуі мүмкін. Керісінше, әрбір (n+m-1, m) қайталанбайтын теруге (n, m) қайталанбалы теру сәйкес келуі мүмкін, осыдан (1, 10) теңдік шығады.
Мысалы,
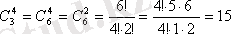
1-ші кестедегі барлық қайталанбалы 15 (3, 4) теру 3 элементтің 4-тен жасалуы сәйкес кортеждермен түгенделген және сәйкес (6, 4) қайталанбайтын терулермен көрсетілген.
Кесте 1
- Толықтауыш шарты бар n элементтерден а
1
а
2
. . . а
n
тұратын қайталанбалы орналастырудың мүмкіншіліктерінің бәрін қарастырамыз. Олардың әрбіреуінде m
1
- элементтердің бірінші түрі, m
2
- элементтердің екінші түрі, және жалпы айтқанда b
i
- элементтердің і-ші түрі,
 .
.
Әрине, b
1
+b
2
+…+b
r
=n теңдігі орындалады. M
i
элементтердің і-ші түрін
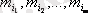 өзгешеліктегі элементтерінің барлығы әр түрлі болады да және одан n! алмастыру шығады.
өзгешеліктегі элементтерінің барлығы әр түрлі болады да және одан n! алмастыру шығады.
Сондықтан, орналастырудың негізгі бастапқы саны шығады, ол
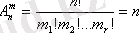 тең де, мұнда
тең де, мұнда
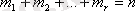 болады. Бұл сан полиномдық (көпмүшеліктік) коэффициент деп аталады, ол (х
1
+х
2
+ . . . +х
r
)
n
полиномының айнымалы шамалары дәрежелер бойынша жіктелген
болады. Бұл сан полиномдық (көпмүшеліктік) коэффициент деп аталады, ол (х
1
+х
2
+ . . . +х
r
)
n
полиномының айнымалы шамалары дәрежелер бойынша жіктелген
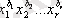 көбейтіндінің коэффициентіне тең болады. r=2 болғанда, биномдық коэффициенттің жеке түрін көрсетеді.
көбейтіндінің коэффициентіне тең болады. r=2 болғанда, биномдық коэффициенттің жеке түрін көрсетеді.
- Кіретін және шығатын негізінің қолдануына тағы бір мысал ретінде тәртіпсіздік есебі беріледі, оның басқаша аты кездесу туралы есеп.
Кез келген
 осындай 1, 2, 3, . . . , n сандардан а
1
а
2
. . . а
n
үшін қанша алмастыру жасауға болады?
осындай 1, 2, 3, . . . , n сандардан а
1
а
2
. . . а
n
үшін қанша алмастыру жасауға болады?
Бұл санды D n арқылы белгілейміз және
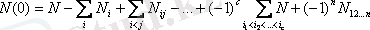 (*)
(*)
формуланы қолданамыз. Мұнда N элементтердің а
1
а
2
. . . а
n
алмастырулары, бұл n!-ге тең, ал Р(с) қасиеті
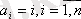 теңдігімен өрнектеледі. Онда
теңдігімен өрнектеледі. Онда
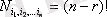
 орында белгілі символ қалдыратын алмастырулардың саны.
орында белгілі символ қалдыратын алмастырулардың саны.
Одан әрі
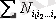
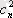 қосылғыштары бар тәсілдердің санымен 1, 2, . . . n-нен таңдалып алынған
қосылғыштары бар тәсілдердің санымен 1, 2, . . . n-нен таңдалып алынған
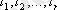 . (*) формуланы қолданып, N(0) табамыз.
. (*) формуланы қолданып, N(0) табамыз.
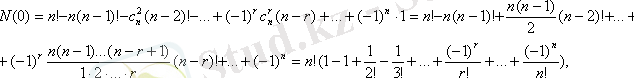
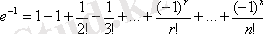
Сондықтан
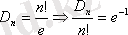 , N(0) =D
n
, N(0) =D
n
- Бірнеше көптеген заттарды қандай да бір саны бар жәшіктерге орналастыру тәсілдерінің санын анықтау үшін, берілген шектеулі шарттардың орындалуы тиіс.
Егер екі жиын Х, Ү берілсе және де X=m, Y=n, Х - заттар жиыны, Ү - жәшіктерден тұратын жиын, y
i
=f(x
i
), x
i
- заттардың у
і
жәшіктерге орналастыруы, онда әрбір функция
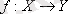 осындай орналастыруды көрсетеді.
осындай орналастыруды көрсетеді.
Ескерту. Жалпы мағынасын кетірмес үшін, әрдайым Х={1, 2, …, m}, ал Y={1, 2, …, n} мүмкіндігі болсын дейік. Егер орналастыруларға ешқандай шектеулер қойылмаса, онда барлық функцияның саны
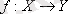 (Х-тің Ү-ке бейнеленуі) n
m
тең, бұдан (n, m) қайталанбалы орналастыру шығады.
(Х-тің Ү-ке бейнеленуі) n
m
тең, бұдан (n, m) қайталанбалы орналастыру шығады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz