Архимедтің математикалық және механикалық еңбектерінің тарихи-ғылыми шолуы


Жоспар
І. Кіріспе
Архимед-ерте заман данышпан ғалымы
ІІ. Негізгі бөлім
Архимедтік денелер
Архимедтің көлемдер туралы теоремалары
Айналу парабола болады
Мәселенің геометриялық жолмен шешілуі
Архимед сперальі
Каноидтар мен сфероидтар туралы
Архимедтік «Дөңгелекті өлшеу»
Псаммит (Қиыршықтар есебі)
Архимед еңбектеріне шолу
ІІІ. Қорытынды
Архимед еңбектерінің математика ғылымының даму жолындағы маңызы.

Архимед-ерте заман данышпан ғалымы
(б. э. дейінгі 285-212 жылдар)
Тарихи - материалдық зерттеулер бойынша бізге мәлім шығармалары Архимед 45-55 жастар арасында жазған. Ғалым басқа уақытта Сиранузы бекіністерін салуды басқарған, соғыс қаруларын жетілдіру ісімен шұғылданды. Архимед әскери инженер болды, соғыс машинасы мен кемелер жасауға басшылық етті.
Бұдан 2200 жыл бұрын - академик А. Н. Крылов барлық замандар мен барлық халықтардың асқан ұлы математигі Архимед кеменің жүзгіштігі жөніндегі мәселелердің бәрін шешетін негізгі заңды тапты және оны дәлелдеп шықты.
Архимедтік денелер
Жақтары әр түрлі бірнеше көпжақтар, ал көпжақты бұрыштарды өз ара тең болған көпжақтар жартылай дұрыс немесе «архимедтік көпбұрыштар» деп аталады. Архимед бес түрлі дұрыс көпжақтардан, басқа он үш түрлі жартылай дұрыс көпжақтар болатындығын тапты олар архимедтік денелер деп аталады. Дұрыс көпжақтар көп зерттелді, сол зерттеу нәтижелерінің бірі Л. Эйлердің мына теоремасы: « Дөңес дұрыс көпжақтардың төбелері мен жақтары сандарының қосындысынан қырлары санын шегерілгендегі қалдық екіге тең.
Т+Ж-Қ=2
Т-төбе саны, Ж-жақ саны, Қ-қыры саны
Куб пен паралелепипедтте
8төбе+6жақ-12қыр=2
Үшбұрыш пирамида
4төбе+4жақ-6қыр=2
Октаэдр
6төбе+8жақ-12қыр=2
Архимед (б. э. дейінгі 285-212 жылдар) -ерте заманның данышпан ғалымы. Ол біздің жыл санауымыздан бұрынғы 285 жылдары Сицилия аралындағы Сиракуз қаласында туған.
Архимедтің өзінің айтуы бойынша оның әкесі Фидий үлкен астроном болған және Күн мен Айдың диаметрлері туралы бірнеше еңбек жазған.
Архимед алғашқы кезде білімді әкесінен үйреніп, кейін сол кездегі ғылым ордасы Александрияға барған.
Өзінің бүкіл өмірі бойы Архимед Александриялык ғалымдар Эратосфенмен, Кононмен, Досифеймен достық байланысы күшті болған; Александрияда өзінің еңбектерін жарыққа шығарып, ондағы ғылым жолын қуған жолдастарына қандай жаңалықтар ашқанын хабарлап отырған. Бірақ бұл жаңалықтарының қандай жолмен ашылғанын, қалай дәлелдегенін айтпаған. Архимед өзінің «Спиральдар туралы» деген шығармасының алғы сөзінде былай дейді: «Табылған жаңалықтардың шешу сырын айтпайтыным, әр математик өз бетімен шешіп, дүниенің рақатын біліп сүйсініп көрсін деймін».
Архимед кейбір есептердің шартын әдейі теріс беріп, қайсы-бір атақ құмар жолдастарын қиын жағдайларға душар еткен кездері де болыпты.
Архимед тек таза математикамен ғана шұғылданып қоймай астрономиямен де, механикамен де, техникамен де шұғылданған ғалым.
Архимед туралы біраз аңыздарға тоқтап кетейік.
Патша Гиеронның алтын тажы туралы аңыз жұрттың көпшілігіне белгілі. Дегенмен айта кетейік. Патша Гиерон өзінің тажын Архимедке көрсетіп, осы таж таза алтыннан жасалған ба, жоқ әлде қоспасы бар ма, осыны біліп берші депті-міс. Архимед біраз ойланып журіп бір күні ваннаға тусіпті де, оның ішінде өзінің біраз жеңілдегенін сезіпті. Сол-сол-ақ екен, ваннадан секіріп шығып, киінбестен «Эврика, эврика!» («Таптым, таптым!») деп көшеге жугіріп шығыпты.
Оның таптым дегені не? Оның тапқаны таждың көлемін анықтау жолы. Ыдыстың бетінен келтіріп толтыра су құйып, оның ішіне тажды салса, су асып төгілер еді. Міне осы асып төгілген суды өлшеп, таждың көлемін табуға болады. Асып төгілген судың салмағы тажға су тарапынан тускен қысым күштің шамасы болып табылатындығын Архимед бірден байқаған.
Егер таждың көлемі белгілі болса, оның меншікті салмағын табу тіпті қиын емес.
Таждың меншікті салмағын тауып алып, оны таза алтынның меншікті салмағымен салыстырып таждың таза алтыннан не қоспадан жасалғанын айтуға болады.
Патша Гиерон Мысыр патшасы Птоломейге сыйлықка «Сиракосию» атты кеме жасатыпты. Бұл кемені сол ерте замандағы техниканың кереметі деп айтуға болады. Бұл кеменің ауырлығы сонша, тіпті оны суға түсіру тіпті қиын болған. Осы кемені жасаған инженерлер, техниктер оны суға түсірудің ешбір амалын таппапты. Мұның амалын тапқан Архимед болыпты.
Архимед бірнеше блоктар системасын құрып, осы машинаның көмегімен бір-ақ адам - патшаның өзі ауыр «Сиракосию» кемесін қара жерден суға түсіріпті-міс. Осыдан кейін патша Гиерон: «Бүгіннен бастап біздің Архимед не айтса да, біз оған сенетін боламыз», - депті.
Архимед жаудың кемесін өртеп жіберетін айна ойлап тауыпты-мыс.
Римдіктер Сиракузды бірнеше рет жаулап алмақшы болады. Бірақ Архимед ойлап тапқан лақтырғыш машина римдіктерге мүмкіндік бермепті. Әскер басқарушы, римдік қолбасшы Марцелл: «Архимед сияқты Бриареймен ұрысқаннан гөрі бүтін әскермен ұрысу анағұрлым онай екен депті-міс».
Архимедтің тағы да бір ойлап тапқан тамаша машинасы суды өте тереңнен жердің бетіне шығарып төгетін шексіз Винт. Архимедтің бұл Винті Мысырда осы уақытқа дейін қолданылады. Архимедтің көп айтыла беретін мынадай қанатты сөзі бар: «Аяқ тірейтін орын тапшы, Жерді орнынан қозғалтайын». Архимед тамаша планетарий (мұны «аспан сферасы» деп те айтады) орнатқан. Мұнда ол планеталардың қозғалысын, Қүннің, Айдың тұтылуын көрсеткен. Біздің жыл санауымыздан бұрынғы 212 жылы римдіктер Сиракузды жаулап алады. Бұл кезде Архимед жетпістен асқан болатын. Архимедті римдік солдат өлтіреді. Архимедтің өлімі туралы Плутарх былай дейді: «Қолында қылышы бар римдік солдат өлтірейін деп Архимедке төнеді. Сонда оған Архимед есебімді шығарғанша бірнеше минут кідіре тұр, ол солдаттың не істемек болғанын айту қиын, өлтірмек болды ма әлде Марцеллға апармақ болды ма, Архимед оны тыңдамағаннан кейін, ол ашумен Архимедті өлтіре салады». Бұдан бергі жерде шыққан мынадай да аңыз бар: Архимед римдік солдатқа: «Ей, адам, менің чертёжіме тиюші болма!» - депті (сурет) . Цицеронды таң қалдырмақ болып Марцелл Архимедтің планетарийін Римге алып келіпті. Бұл жерде Архимедтің «Шар және цилиндр туралы» деген еңбегін айтпай болмайды. Осы еңбегінде Архимедтің өзіне өте ұнағаны-оның атақты екі теоремасы: «Шар бетінің ауданы оның үлкен дөңгелегінің ауданынан төрт есе артық», «Шардың көлемі оған сырттай сызылған цилиндр көлемшің
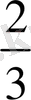 -не тең».
-не тең».

Ей, адам, менің чертёжіме тиюші болма! - депті Архимед римдік солдатқа.
Архимед бейітінің басына осы фигуралардың (цилиндрге іштей сызылған шардың) кескіні ескерткіш есебінде койылыпты. Цицерон Сицилияда квестор болып тұрғанда осы ескерткішті көріпті-міс. Енді Архимедтің ғылми еңбектеріне келейік. Оның математикалық еңбектерін толық талдау үшін бір емес бірнеше кітап жазу керек. Сондықтан біз тек қысқаша шолу жасаймыз. Көп уақытқа дейін осындай жоғары сатыдағы еңбектерді Архимед қандай жолмен жазғаны, ондағы ақиқаттарды қандай әдістермен дәлелдегені белгісіз болып келді. Бұл жөнінде әркімде әр түрлі көзқарастар болды. Мәселен, XVII ғасырда болған ағылшын математигі Валлис былай дейді: «Арттағы ұрпаққа зерттеулерінің сырын білдірмес үшін, тек нәтижелері дұрыс болса болғаны деген оймен Архимед өзінің зерттеулерінің ізін әдейі жойып жіберген болар». Шынында жалғыз Архимед емес, ерте замандағы математиктердің бірсыпырасы өздерінің зерттеу әдістерін кейінгі ұрпақтан жасырғаны рас. Сондықтан жаңа заманның математиктері ерте замандағы қайсыбір математиктердің әдістерін қайтадан қалпына келтіргеннен гөрі жаңа әдісті ойлап тапқан жеңіл деп білді. Архимедтің жоғалған әдісі табылды. Оның қалай табылғаны туралы И. Г. Башмакова өзінің «Ертедегі Грециядағы математика тарихы жайындағы лекциялар» атты еңбегінде былай дейді: «Метод туралы Эратосфенге хат» («Эфод») 1906 жылы табылды. Петербург университетінің приват-доценті Попадопуло-Керамевс, Иерусалим монастырьлерінің бірінің кітапханасынан ертедегі грек қолжазбасының үстінен христиан тексі жазылған пергаментті ' тапқан. Ол біраз үзінділерді жазып алған. Олар Архимедтің еңбегі екенін Дания тарихшысы Гейберг бірден білген. Сөйтіп, ол Архимедтің жоғалып кетті деген «Методын» қалпына келтіреді». Енді осы «Метод» атты Архимед шығармасының қысқаша мазмұнын берейік. «Метод туралы» Эратосфенге жазған хатында Архимед рычаг принципі бойынша жаңа математикалық ақиқаттарды қалай табуға болатындығын баяндайды: «Мен сені байыпты ғалым, үздік философ деп есептеймін, сондықтан осы хатымда бір ерекше методты баяндауды және оны саған түсіндіруді орынды деп таптым; бұл методты пайдаланып кейбір математикалық мәселелерді механиканиканың көмегімен зерттеу үшін көмекші жақсы тәсіл тауьш аласын».
Архимедтің көлемдер туралы теоремалары
«Шар мен цилинр туралы» деген екі кітабында және «Эратосфенге хат (Эфод) » деген еңбегінде ұлы Архимед Евклид жинаған стериометриялық мәліметтерді байыатры дамытты.
Архимедте Евклидше бір көлемді, мысалы шардың көлемін, цилиндр мен конустың көлемдерін салыстыра отырып, көлем бірлігін қолданбай мынадай теоремаларды дәлелдеді.
1. Шарға сырттай сызылған цилиндрдің көлемі шар көлемінен
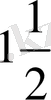 есе артық болады.
есе артық болады.

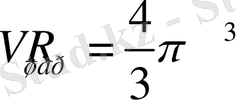
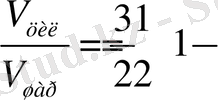
2. Табаны шардың үлкен дөңгелегіне тең, биіктігі шардың радиусына теңконустың көлемі шардың көлемінен 4 есе кіші болады.
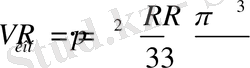
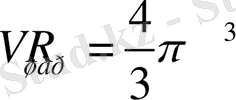
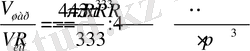
3. Шардың беті оның 4 еселенгенше үлкен дөңгелектің ауданына тең
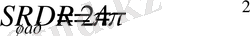

4. Әр шардың көлемі табаны шардың бетіне, ол биіктігі шардың радиусына тең болған конустың көлеміне тең болады.
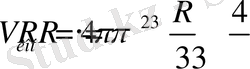
5. Радиустары бірдей, ол биіктіктері шардың диаметрлеріндегі конус, шар және цилиндрдің колемдерінің қатынастары 1:2:3 салдарының қатынасындай болады.

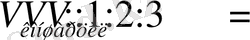
6. Шарды сырттай сызылған цилиндрдің бүйір беті шар бетіне тең.

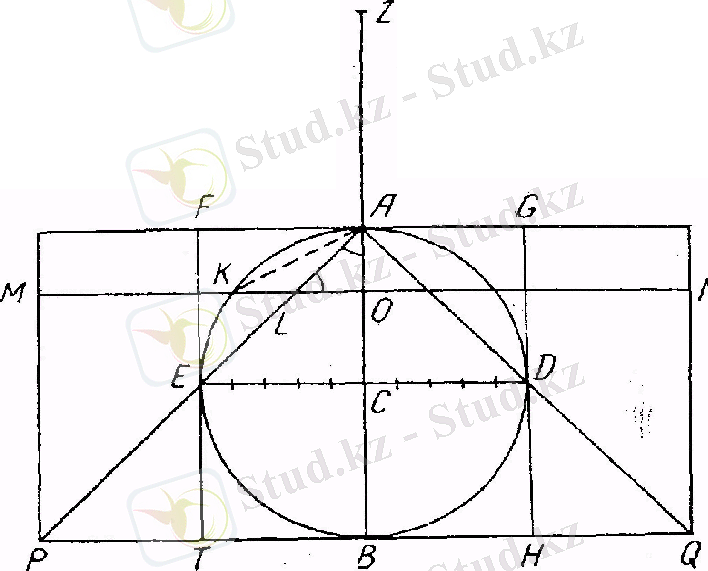 Шардың көлемін табу үшін Архимед қолданған механикалық әдістің мәнісі не? Айталық радиусы АС=R шар, табандарының радиустары 2R, биіктіктері де 2R конус пен цилиндр берілсін (сурет) . Бұл суретте PZ
-
конус пен цилиндрдің осі, ал PQ
-
олардың табандарының диаметрі, МN кез келген горизонталь жазықтықтың ocі. Бұл жазықтық цилиндр, шар және конусты радиустары ОМ, ОК және ОL дөңгелектер бойымен қиып өтеді. Ал чертёжден көретініміз.
Шардың көлемін табу үшін Архимед қолданған механикалық әдістің мәнісі не? Айталық радиусы АС=R шар, табандарының радиустары 2R, биіктіктері де 2R конус пен цилиндр берілсін (сурет) . Бұл суретте PZ
-
конус пен цилиндрдің осі, ал PQ
-
олардың табандарының диаметрі, МN кез келген горизонталь жазықтықтың ocі. Бұл жазықтық цилиндр, шар және конусты радиустары ОМ, ОК және ОL дөңгелектер бойымен қиып өтеді. Ал чертёжден көретініміз.
 Екінші жағынан,
Екінші жағынан,
 яғни
яғни
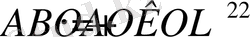
Бұл теңдіктің екі жағын да
АВ
-ге көбейтсек, онда
 немесе
немесе
 (5)
(5)
АВ және АZ=АВ кесінділерін тіреу нүктесі А нүктесімен дәл келетін рычагтың иіндері деп қарасақ, сонда (5) теңдіктен мынадай қорытындыға келеміз: егер шардың дөңгелек қимасы π ОК 2 -ты, конустың дөңгелек қимасы π ОL 2 -ты Z нүктесіне көшірсек, онда олар А нүктесіне қатысты айтқанда орнында қалған цилиндрдің дөңгелек қимасы π АВ 2 = πОМ 2 - пен «теңелген» болар еді. Мұндай қорытынды шардың, конустың және цилиндрдің бір горизонталь жазықтықта жатқан кез келген басқа қималары үшін де дұрыс болатындығын Архимед ескертеді. Және Архимед былай дейді: «Цилиндр сол сияқты шар мен конус осындай дөңгелек қималармен толтырылған, сондықтан орнында қалатын цилиндр А нүктесіне қатысты алғанда шар және конуспен теңгеріледі, егер кейінгі екеуін ауырлық центрлері Z, нүктесінде болатындай етіп рычаг иінін Z нүктесіне келтіріп бекітсек».
Орнында қалып отырған цилиндрдің ауырлық центрі АВ кесіндісінің ортасы С нүктесінде.
Цилиндрдің көлемін и, шардың көлемін υ , конустың көлемін ω арқылы белгілейік. Сонда Архимедтің қорытындысы бойынша

Демек,
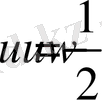
Ал Евдокс теоремасы бойынша
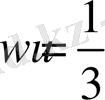
Ендеше,

Міне осы шыққан нәтиже Архимедтің өз еңбегінде былай тұжырымдалған: «Шардың көлемі табаны осы шардын үлкен дөңгелегі, ал биіктігі оның диаметрі болып табылатын және оған сырттай сызылған цилиндр көлемінің үштен біріне тең».
Екінші жағынан, шардың көлемі
ҒGНТ
кіші цилиндр көлемінің
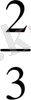 -не тең. Бұл қорытынды Архимедтің еңбегінде былай тұжырьшдалған: «Шарға сырттай сызылған цилиндр одан
-не тең. Бұл қорытынды Архимедтің еңбегінде былай тұжырьшдалған: «Шарға сырттай сызылған цилиндр одан
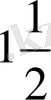 есе артық болады». Бұл нәтижені басқаша да тұжырымдауға болады. Шар табаны оның үлкен дөңгелегіне, биіктігі радиусына тең конустан төрт есе артық болады. Осыдан келіп Архимед «Шар бетінің ауданы оның төрт үлкен дөңгелегінің ауданына тең» деген ойға келеді. Оның дәлелі мынау: егер әрбір дөңгелек ауданы табаны оның шеңберінің ұзындығына, биіктігі радиусына тең үшбұрыштың ауданына тең болса, онда дәл осы сияқты, шар беті табаны осы шар беті ауданына, биіктігі оның радиусына тең конус бетіне тең болуы керек. Дәл осы баяндалып отырған методпен сфероидтың, яғни айналу эллипсоидының да, көлемін табуға болады. Айналу эллипсоид көлемі оған сырттай сызылған цилиндр көлемінің
есе артық болады». Бұл нәтижені басқаша да тұжырымдауға болады. Шар табаны оның үлкен дөңгелегіне, биіктігі радиусына тең конустан төрт есе артық болады. Осыдан келіп Архимед «Шар бетінің ауданы оның төрт үлкен дөңгелегінің ауданына тең» деген ойға келеді. Оның дәлелі мынау: егер әрбір дөңгелек ауданы табаны оның шеңберінің ұзындығына, биіктігі радиусына тең үшбұрыштың ауданына тең болса, онда дәл осы сияқты, шар беті табаны осы шар беті ауданына, биіктігі оның радиусына тең конус бетіне тең болуы керек. Дәл осы баяндалып отырған методпен сфероидтың, яғни айналу эллипсоидының да, көлемін табуға болады. Айналу эллипсоид көлемі оған сырттай сызылған цилиндр көлемінің
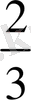 -не тең. Егер айналу параболоидты осіне перпендикуляр жазықтықпен қисақ, онда қиылып түскен сегмент көлемі табаны мен осі параболоид тікіндей конус көлемінен
-не тең. Егер айналу параболоидты осіне перпендикуляр жазықтықпен қисақ, онда қиылып түскен сегмент көлемі табаны мен осі параболоид тікіндей конус көлемінен
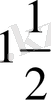 есе артық болады.
есе артық болады.
Мұнымен бірге Архимед осы айналу параболоиды сегментінің ауырлық центрі жөнінде мынадай теореманы дәлелдейді.
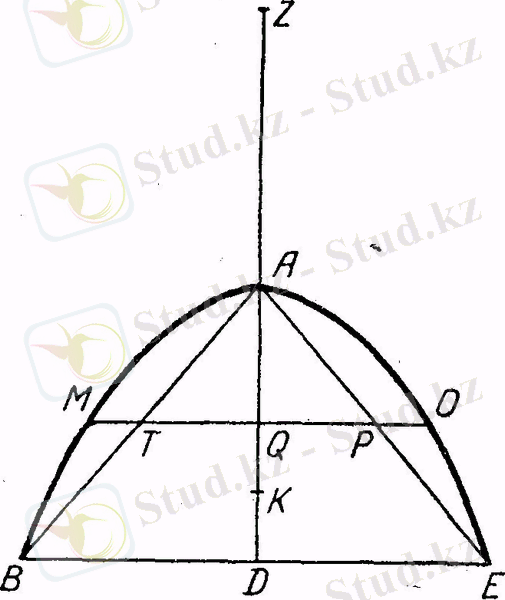 Параболоидтык сегменттің ауырлық центрі
К
оның осі AD-ні 2 : 1 катынасында бөледі (сурет) .
Параболоидтык сегменттің ауырлық центрі
К
оның осі AD-ні 2 : 1 катынасында бөледі (сурет) .
Мұны дәлелдеу үшін, Архимед төбесі
А
нүктесінде болатындай етіп
АВЕ
конусын сегментке іштей сызады және D
А-
ны
АD = АZ
кесіндісіне созады. Сейтеді де A-ны тіреу нүктесі деп есептеп, Z
А
рычагын қарастырады.
ВAЕ
парабола жазықтығында жатқан
ВЕ
түзуіне қалауымызша
ОМ
параллелін жүргізсек, сонда

Бұл арадан мынадай қорытындыға келуге болады: өз орнында тұрған
ОМ
дөңгелегі Z нүктесіне жылжытылған
РТ
дөңгелегімен теңгерілуі керек. Демек, өз орнында қалған параболоидтық сегмент Z нүктесіне жылжытылған конуспен теңгеріледі. Ал параболоидтық сегмент салмағы конус салмағынан есе
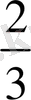 артық, олай болса,
А
Z және
АК
иіндерінің бір-біріне қатынасы 3:2 қатынасындай болады. Сөйтіп, Архимед теоремасы дәлелденді.
артық, олай болса,
А
Z және
АК
иіндерінің бір-біріне қатынасы 3:2 қатынасындай болады. Сөйтіп, Архимед теоремасы дәлелденді.
Міне осы әдіспен Архимед жарты шардың, шар сегментінің, сфероидтық сегменттің, айналу гиперболоиды сегментінің ауырлық центрлерін, шар сегменті мен сфероидтық сегменттің көлемдерін тапты.
Егер табаны квадрат тік призмаға, табаны квадратқа іштей сызылған дөңгелек болатын цилиндрді іштей сызса және осы призманы төменгі табанының центрі мен жоғарғы табанының қабырғасы арқылы өтетін жазықтықпен қиса, онда цилиндрлік бетпен, көлбеу жазықтықпен және табан жазықтығы мен шектелген цилиндр бөлігі толық призманың
-не тең болады Бұл теореманы Архимед өзінің механикалық әдісімен де және геометриялық әдіспен де дәлелдейді.
Егер берілген кубқа осьтері өз ара перпендикуляр екі цилиндрді іштей сызса, онда бұлардың ортақ көлемі куб көлемінің
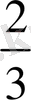 -не тең болады:
-не тең болады:
Бұл теореманың дәлелдемесі Архимедтің айтылып отырған еңбегінде жоқ.
Енді параболалық сегмент ауданын Архимед өзінің механикалық әдісімен қалай тапты, соған тоқтайық.
Бір жағынан
АГ
түзуімен, екінші жағынан
АВГ
параболасымен қоршалған параболалық сегментті қарастырайық (сурет) .
АГ
табанының қақ ортасы
В
арқылы парабола осіне параллель
DВЕ
түзуін жүргізейік. Сонда
АВГ
сегментінің ауданы
АВГ
үшбұрышы ауданынан
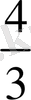 есе артық дейді Архимед. Мұны дәлелдеу үшін
Г
нүктесі арқылы параболаға жанама, сонан соң
А
нүктесінен осы жанамамен түйіскенше
ОВЕ-
ге параллель
А
Z түзуін жүргізейік. Енді
ГВ
кесіндісін солға қарай созайық та, осы созындының бойына
КӨ = КГ
кесіндісін салайық (сурет) .
есе артық дейді Архимед. Мұны дәлелдеу үшін
Г
нүктесі арқылы параболаға жанама, сонан соң
А
нүктесінен осы жанамамен түйіскенше
ОВЕ-
ге параллель
А
Z түзуін жүргізейік. Енді
ГВ
кесіндісін солға қарай созайық та, осы созындының бойына
КӨ = КГ
кесіндісін салайық (сурет) .
Бұдан соң ГӨ -ні тіреу нүктесі К болатын рычаг деп қарауға болады. Параболаның кез келген Ө нүктесі арқылы ЕО -ге параллель МР түзуін жүргізейік.
Параболаның Архимед белгілі деген қасиеттері бойынша

Ендеше

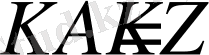 ,
,
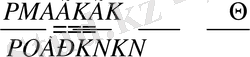 (6)
(6)
Егер рычагтың екінші ұшы Ө нүктесіне РО = ТН кесіндісін ілсек, ол, рычагтың заны бойынша, өз орнында тұрған МР кесіндісімен теңгеріледі.
(6) қатынастардан мынадай қорытындыға келуге болады: осы айтылып отырған екі кесіндінің салмақтары рычагтың иіндеріне кері пропорционал. Бұл қорытынды АГ Z үшбұрышының ішінен жүргізілген DЕ- ге параллель барлық түзулер үшін дұрыс. Бұл түзулер өз орындарында қалып, Ө нүктесіне жылжытылған парабола ішіндегі өздерінін, бөліктерімен теңгеріледі.
Архимед былай дейді: «Үшбұрыш АГ Z мына РМ сияқты сызықтардан, параболалық сегмент АВГ мына РО сияқты сызықтардан тұрады. Ендеше, өз орнында қалатын АГ Z үшбұрышы ауырлық центрі Ө нүктесінде болатын параболалық сегментпен теңгеріледі».
АГ
Z үшбұрышының ауырлық центрі
X
нүктесінде, ал
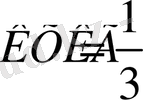 .
Параболалық сегмент ілінген
КӨ
иіні
КХ
иінінен үш есе артық. Үшбұрыш
АГ
Z сол сегментпен теңгерілетін болғандықтан, үшбұрыштың салмағы сегменттің салмағынан үш есе артық. Ал
АГ
Z үшбұрышы
АГК
үшбұрышынан екі есе артық, демек,
АГ
Z
.
үшбұрышы
АВГ
үшбұрышынан төрт есе артық.
.
Параболалық сегмент ілінген
КӨ
иіні
КХ
иінінен үш есе артық. Үшбұрыш
АГ
Z сол сегментпен теңгерілетін болғандықтан, үшбұрыштың салмағы сегменттің салмағынан үш есе артық. Ал
АГ
Z үшбұрышы
АГК
үшбұрышынан екі есе артық, демек,
АГ
Z
.
үшбұрышы
АВГ
үшбұрышынан төрт есе артық.
Сөйтіп, параболалық сегмент ауданы
АВГ
үшбұрышы ауданының
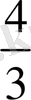 -не тең болады. Бұл дәлелдеме шын мәнісінде нық емес, бірақ нәтиженің дұрыстығына әбден көз жеткізуге болады деп ескертеді Архимед.
-не тең болады. Бұл дәлелдеме шын мәнісінде нық емес, бірақ нәтиженің дұрыстығына әбден көз жеткізуге болады деп ескертеді Архимед.
 Енді Архимед осы мәседелерді геометриялық жол мен қалай шешкеніне біраз тоқтап кетейік.
Енді Архимед осы мәседелерді геометриялық жол мен қалай шешкеніне біраз тоқтап кетейік.
Параболалық сегмент ауданын табуда Архимед негізін Евдокс салған түгесу методы идеясын пайдаланады және әрі қарай дамытады.
Парабола осіне перпендикуляр ВГ түзуімен қиылған параболалық сегментті алайық та, Г нүктесінде параболаға жанама, сонан соң В нүктесінен осы жанамамен түйіскенше парабола осіне ВО параллелін жүргізейік.
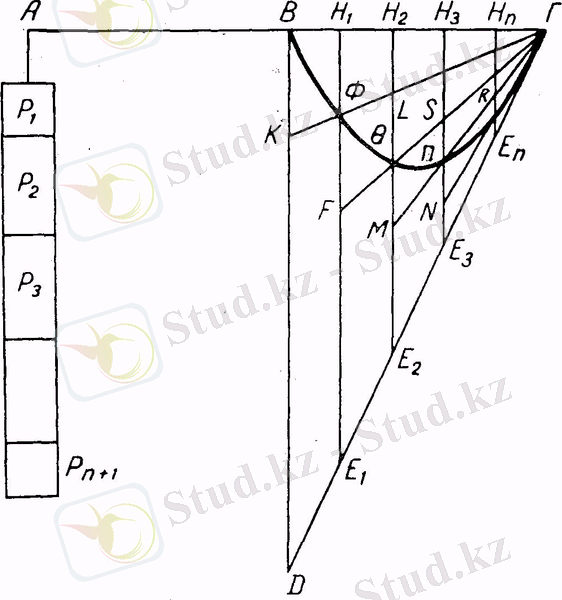
Енді ВГ -ні тең п бөлікке бөлейік те, бөлу нүктелерінен жанамамен қиылысқанша оське параллель түзулер жүргізейік. Бұдан соң Г нүктесін параллельдердің параболамен қиылысу нүктелерімен қосайық (сурет) .
Үшбұрыш ВГD мына КВН 1 Ф, ҒӨН 2 Н 1 , МПН 3 Н 2 , . . . , МОН n Н 3 трапециялардың және Е n Н n Г үшбұрыштың үш есе қосындысынан кіші де, ал ФLН 2 Н 1 , ӨSН 3 Н 2 , ПRН n Н 3 трапециялардың және ОГН n үшбұрыштың үш есе қосындысынан артық дейді Архимед.
Мұны дәлелдеу үшін Архимед
ГВ
-ні
ВГ=ВА
кесіндісіндей әрі карай созып,
АГ
-ні тіреу нүктесі
В
болатын рычаг деп карайды; бұл рычагтың екінші
А
ұшына ол D
Е
1
Н
1
В,
Е
1
Е
2
Н
2
Н
1
, Е
2
Е
3
Н
3
Н
2
,
. . .
Е
3
Е
п
Н
п
H
3
трапецияларымен және
Е
п
Н
п
Г
үшбұрышымен теңгерілетін Р
1
Р
2
,
. . . ,
Рп+і
аудандарды ілді. Сонда осы аудандардың барлығының қосындысы
ВГ
D үшбұрышымей тепе-тең болуы керек, олай болса, бұл қосынды әлгі үшбұрыштың
 -не тең.
-не тең.
(6) пропорция бойынша
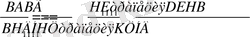
сол сияқты,
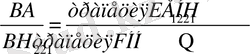
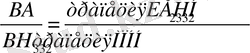
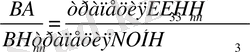
Сөйтіп, DЕ 1 Н 1 В, Е 1 Е 2 Н 2 Н 1 , . . . трапецияларын Н 1 , H 2 , . . . , «оң» жақ ұштарынан іліп қойса, онда олар А нүктесіне ілінген КФН 1 В, ҒӨН 2 Н 1 , . . . трапецияларымен теңелер еді. Ал егер де оларды бұрышынан ілмей, ВН 1 , Н 1 Н 2 , . . . қабырғаларынан ілсе, онда олар Р 1 , Р 2 , - аудандарымен теңгерілер еді. Демек, Р 1 , Р 2 , . . . аудандары КФН 1 В, ҒӨН 2 Н 1 , . . . трапецияларынан кіші. Олай болса, бұл аудандардың қосындысы Р 1 + Р 2 + . . . +Р п+1 мына КФН 1 В, ҒӨН 2 Н 1 . . . , NОН п Н 3 трапециялары мен Н n Е n Г үшбүры-шының косындысынан кіші.
Ал қосынды
Р
1
+ Р
2
+ . . . + Р
п+1
үшбұрыш BГD-нің
 -не тең; ендеше бұл үшбұрыштың
-не тең; ендеше бұл үшбұрыштың
 -і сол трапециялар мен
Н
n
Е
n
Г
үшбұрышының қосындысынан кем. Осы айтылып отырған трапециялар мен үшбұрыш параболалық сегменттен тыс жатыр.
-і сол трапециялар мен
Н
n
Е
n
Г
үшбұрышының қосындысынан кем. Осы айтылып отырған трапециялар мен үшбұрыш параболалық сегменттен тыс жатыр.
ВГD
үшбұрышының
 і параболалық сегменттің ішінде жатқан
ФLН
2
Н
1
SӨН
3
Н
2
, ПR. Н
n
Н
3
трапециялар мен
Н
n
ГО
үшбұрышының қосындысынан артық екенін Архимед дәл жаңағыдай дәлелдейді.
і параболалық сегменттің ішінде жатқан
ФLН
2
Н
1
SӨН
3
Н
2
, ПR. Н
n
Н
3
трапециялар мен
Н
n
ГО
үшбұрышының қосындысынан артық екенін Архимед дәл жаңағыдай дәлелдейді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz