Бүтін-бөлік ұғымы, жиынның қуаты және натурал сандардың бөлінгіштік теоремалары


Бүтін және бөлік
Дара күйінде бөлмайтын, бірақ барлығы бірігіп, жаңа қасиеттер мен заңдылықтарды тудыратын байланыс пен заттар жиынының арасындағы қатысты бейнелеушіні бүтін дейміз. Бүтінді құраушы әр бір затты оның бөлігі дейміз.
Бүтін алдымен тұтас күйінде қабылданады. Мұнан соң, арнайы жасалған талдау бойынша бөліктерге жіктеледі. Сонында, оларды ойша топтау арқылы бүтін туралы тұжырым жасалады.
Әр бір өсімдік, жәндіктер, жануарлар тұтас күйінде бүтін болады. Бүтіннің құрамы күрделі.
Бүтінді тану үшін, оның құрамды бөліктері арасындағы байланыстарды ажырата білген жөн. Математикада бүтін және бөлік категорияларына қатысты проблемалар ең күрделі, шешуі де, шешімі де қиын, көрнекілігі жетімсіз (бой жетпейтін), интуитивтік жолмен қабылданатын (ой бірде жетіп бірде жетпейтін) бұлыңғыр ойлардан тұрады.
Жиын әуелгі ұғымдар қатарына жатады. Ол элементтер деп аталатын құраушылардың құрамын білдіреді. Мысалы, төртбұрыштың қабырғаларының жиыны, қазақ альфавитіндегі әріптер жиыны, бір отар қой - жиын, бір үйір жылқы - жиын, натурал сандар жиыны, теңдеудің шешімдерінің жиыны және т. с. с.
Құраушы элементтерінің саны шектелген жиынды шектеулі, ол элементтерінің саны шектелмеген жиынды шектеусіз дейміз. Мысалы, бес бұрышты көпбұрыштың диагоналдарынан тұратын жиын шектеулі жиын. Сол сияқты, қырманда жатқан бидай дәндерінің жиыны да, шектеулі болады. Натурал сандар жиыны, жазықтықтағы барлық түзулер жиыны, жазықтықта бір нүктеде қиылысатын барлық түзулер жиыны, рационал сандар жиыны шектеусіз жиынға жатады.
Шектеусіз жиындар саналымды және саналымсыз болып бөлінеді. Құраушы элементтерін натурал сандар тізбегімен белгілеп шығуға болатын жиындар саналымды болады. Егер бұл шартты жүзеге асырарлық мүмкіндік болмаса, онда жиын саналымсыз болады. Мысалы, түзу жолындағы нүктелер, кесінді құраушы нүктелер саналымсыз жиын құрайды.
Құраушы элементтерінің саны бірдей жиындарды қуаттас дейміз. 10 дәптерден тұратын жиын, 10 суреттен тұратын жиын, 10 қояннан тұратын жиындар қуаттас болады.
Шектеусіз жиындарды элементтерінің санына қарап қуаттастығын анықтауға болмайды. Шектеусіз жиындардың қуаттастығын анықтау үшін олардың элементтерінің арасында өзара бір мәнді сәйкестік тағайындау керек. Барлық натурал сандар жиыны мен барлық жұп натурал сандар жиыны қуаттас. Өйткені, әр бір п натурал санына 2п натурал санын және керісінше, сәйкес қоюға болады. Сол сияқты, кесінді бойындағы нүктелер жиыны мен сол кесіндідегі иррационал нүктелер жиыны қуаттас.
Саналымсыз жиынды латынша үздіксіз ұғымын білдіретін континуум сөзімен айтады. Мысалы, кез-келген кесінді байындағы нүктелер жиыны, түзу бойындағы нүктелер жиыны, тұйық дөңгөлек ішіндегі нүктелер жиыны, шар бойындағы, сфера бойындағы, пирамида, призма бойындағы нүктелер жиынның қуаты континуум болады.
Жиынның қуаты ондағы элементтер санын жалпылайды. Бір жиын екінші бір жиынды қамтуы, яғни екінші жиын бірінші жиынның бөлігі болуы мүмкін. Бұл жағдайда, екінші жиын қуаты бірінші жиын қуатынан кем деп айтуға мүмкіндік туады. Барлық бұл жөнінде бірден кесімді пікір айту қиын.
Элементтерінің арасында өзара бір мәнді сәйкестік тағайындалған шектеусіз жиындарды эквивалент жиындар дейміз.
Бөлінгіштік қатысы туралы ұғым
Үлкен натурал сан а -ны кіші натурал сан b-ге бөлгенде қалдық нольге тең болса, а санының b санына бүтіндей бөлінетінін білеміз.
Сондай-ақ, егер натурал сан
а
натурал сан
b
- ден артық болса, онда әрқашан да мынадай теңдікті қанағаттандыратын q мен r екі санды табуға болатындығы да тағайындалады:
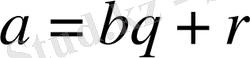 . Мұндағы q - үлкен санды (
а
-ны) кіші санға
(b-ге)
бөлгендегі бөлінді де,
r
- қалдық. Қалдықсыз бөліну натурал сандардың осы жалпы қасиетінің бір дербес жағдайы екендігі, атап айтқанда,
r
= 0 болып,
а= bq
теңдігі шығатын жағдай екендігі айқын.
. Мұндағы q - үлкен санды (
а
-ны) кіші санға
(b-ге)
бөлгендегі бөлінді де,
r
- қалдық. Қалдықсыз бөліну натурал сандардың осы жалпы қасиетінің бір дербес жағдайы екендігі, атап айтқанда,
r
= 0 болып,
а= bq
теңдігі шығатын жағдай екендігі айқын.
Бұл жағдайда а саны (бөлінгіш) b санының еселігі деп, ал b
саны а - санының бөлгіші деп аталады.а саны b санына бөлінеді, а саны b санының еселігі, b саны а- санының бөлгіші деген сөйлемдердің мағына жағынан бір-біріне барабар екендігін ескертейік.
теңдігіне қарағанда қандай да бір натурал санның (b) еселігі ( а ) ол сан мен екінші бір натурал санның (q) көбейтіндісі болып табылатындығы шығады. Егер
болса, онда болудің мағынасы бойынша а:q = b; демек, а саны q санының да еселігі болып табылады. Бұдан көбейтінді ( а ) өзінің әрбір көбейткіштерінің (b мен q-дың) еселігі болып табылатындығы шығады. Көбейтудын терімділік және ауыстырымдылық заңдарын пайдалана отырып, бұл қорытындының көбейткіштер саны қанша болса да тура болатындығын дәлелдеу оңай.
Дұрысында да, егер
болса, онда терімділік қасиеті бойьшша
, ал бөлудің анықтамасы бойынша
Демек, N саны - көбейткіш а -ның еселігі. Екінші жағынан, егер
болса, онда ауыстырымдылық қасиеті бойынша
терімділік қасиеті бойынша
, ал бөлудін мағынасы бойынша
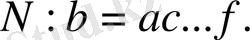
Демек, N - көбейткіш b -нің де еселігі.
Осылайша N саны өзінің басқа да қалған көбейткіштерінің әрқайсысының еселігі болып табылатындығын тағайындауға болады.
Бөлінгіштік қатысын белгілеу үшін ерекше таңба - тігінен орналасқан үш нүкте қолданылатындығын еске саламыз.
Сонда а:b жазуын былай оқу керек: а саны b санына қалдықсыз бөлінеді немес а саны - b санының еселігі. Ал бұл қатыс орындалмайтын болса, онда бүл жағдайда " а саны b -ге бөлінбейді" дейтін боламыз.
Теріс емес бүтін сандардың қосындысының, айырмасының және көбейтіңдісінің бөлінгіштігі.
Практикада бірнеше санның қосындысы (айырмасы көбейтіндісі) берілген санға бөліне ме деген сұрақ туады. Бұл сұраққа мына теоремалар жауап береді.
Қосындысының бөлінгіштігі жөніндегі теорема.
Егер берілген қосындының әрбір қосылғышы бір санға бөлінсе, онда бүкіл қосынды да сол санға бөлінеді.
Берілгені:
және
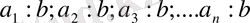
Дәлелдейтініміз:

Бөлу амалының анықтамасына сүйеніп, теореманың шартынан мынадай теңдіктер жазуға болады:
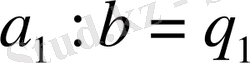 бұдан
бұдан
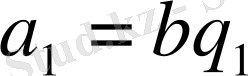
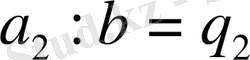 бұдан
бұдан
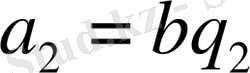
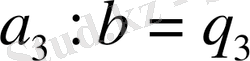 бұдан
бұдан
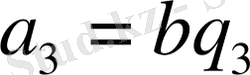
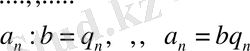
Екінші қатардағы теңдіктерді мүшелеп қосып, мынаны табамыз:
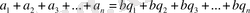
немесе
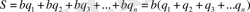
Бұдан
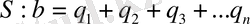
Демек,

Мысал. 24, 20 және 36 сандары 4-ке қалдықсыз бөлінеді.
Бұдан:
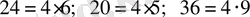
Сандарды қосамыз: 24+20+36=80 немесе
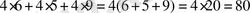 бұдан
бұдан
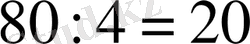 , демек
, демек
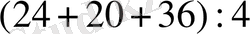
Салдар. 1. Берілген санның кез келген еселігі ол санның әрбір бөлгішінің де еселігі болып табылады.
Мысал. Егер 80 саны 16-ға бөлінсе, ал 16 саны 4-ке бөлінсе, онда 80 саны 4-ке бөлінеді. Демек, егер бірінші сан екінші санға бөлінсе, ал екінші сан үшінші санға бөлінсе, онда бірінші сан үшінші санға бөлінеді.
Салдар. 2. Егер екі қосылғыштың қосындысы және олардың біреуі қандай да бір санға бөлінсе, онда екінші қосылғыш та сол санға бөлінеді.
Көбейтіндінің берілген санға бөлінгіштігі жөніндегі теорема
Егер көбейткіштердің біреуі берілген санға бөлінсе, онда көбейтінді де сол санға бөлінеді.
Дәлелдеуі:
а
және
b
көбейткіштерінің біреуі
п
санына бөлінсін. Егер
а:п
, онда қандай да бір
с
саны табылып,
а = п с
теңдігі орындалады. Осы теңдіктің екі жағын да
b
санына көбейтейік. Сонда
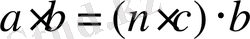 болады. Бұдан
болады. Бұдан
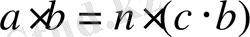 және
және
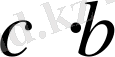 -
теріс емес бүтін сан, яғни
-
теріс емес бүтін сан, яғни
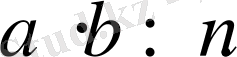 ,
,
Мысалы.
 көбейтіндісі 12-ге бөлінеді, себебі 24 көбейткіші 12-ге бөлінеді.
көбейтіндісі 12-ге бөлінеді, себебі 24 көбейткіші 12-ге бөлінеді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz