Планиметрия

Жоспар
Кіріспе

І Кеңістіктегі түзулер мен жазықтықтар
Түзулер мен жызықтықтарды салу есептері
ІІ Тарау. КӨПЖАҚТАР
2 Геометриялық фигуралардың бар баолуын зерттеу есептері
3 Көпжақтардың қимасын салу есептері
4 Көпжақтардағы метрикалық есептер
5 Айналу денелері. Конус, цилиндр және олардың көпжақтарымен комбинациясы
6 Шар және оның бөліктері
7 Айналудан шығатын фигуралар
8 Нұсқаулар мен жауаптар. Есептерді шешуге нұсқаулар

Планиметрияда фигуралардың барлығы тек бір ғана жазықтықта зерттеледі. Ал, кеңістікте көптеген жазықтықтарды бірге қарастыруға тура келеді.
Стереоиетрия физикалиқ денелердің формасы мен өлшемдерін ондағы элементтердің орналасуын сипаттаиды. Кеңістіктегі фигуралардың басым көпшілігі абстрактілі түрде алынады.
Орта мектеп оқушилары мен педагогика институттары физика-математика факультеттері студенттерінің кеңістік жөніндегі түсініктерін дамыту, кеңістіктегі геометриялық обьектілер арасындағы қатыстарды түсініп оларды ойша көре білу көз алдыға елестете алу геометрияны оқытудағы маңызды мәселелердің бірінен саналады. Бұл әсіресе болашақта техникалық мамандық алатын жастар үшін аса керекті дағды болып табылады.
Қазақ тіліндегі қажетті әдебиеттің жетіспеуі салдарынан физика - математик факультеттерінің сырттай оқитын студенттер стереометрия есептері бойынша орындабйтын бақылаудан қиналады. Олардың быс ым көпшілігі геометриялық дененің бетінің ауданы мен көлемін дайын формулаларыдың көмегімен қиындықсыз есептеп дағдыланған.
Бірақ кеңістіктегі барынша қарапайым фигуралардың өзара орналасуы мен бір – біріне қатысты байланысын өз бетінше анықтау - студенттерге көптеген қиындықтар келтіреді.
Оқушылардың кеңістік жөніндегі түсініктерін дамытудың бірқатар тәсілдері бар, солардың ең маңыздыларының бірі – стереометрия есептерін шешу. Кеңістіктегі фигуралардың қасиеттерін есептер шешуге қолдану болашақта мұғалім болатын студенттердің кеңістікті қабылдауына мүмкіндік береді.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:

Кіріспе
Планиметрияда фигуралардың барлығы тек бір ғана жазықтықта зерттеледі.
Ал, кеңістікте көптеген жазықтықтарды бірге қарастыруға тура келеді.
Стереоиетрия физикалиқ денелердің формасы мен өлшемдерін ондағы
элементтердің орналасуын сипаттаиды. Кеңістіктегі фигуралардың басым
көпшілігі абстрактілі түрде алынады.
Орта мектеп оқушилары мен педагогика институттары физика-математика
факультеттері студенттерінің кеңістік жөніндегі түсініктерін дамыту,
кеңістіктегі геометриялық обьектілер арасындағы қатыстарды түсініп оларды
ойша көре білу көз алдыға елестете алу геометрияны оқытудағы маңызды
мәселелердің бірінен саналады. Бұл әсіресе болашақта техникалық
мамандық алатын жастар үшін аса керекті дағды болып
табылады.
Қазақ тіліндегі қажетті әдебиеттің жетіспеуі салдарынан
физика - математик факультеттерінің сырттай оқитын студенттер
стереометрия есептері бойынша орындабйтын бақылаудан қиналады.
Олардың быс ым көпшілігі геометриялық дененің бетінің ауданы
мен көлемін дайын формулаларыдың көмегімен қиындықсыз есептеп
дағдыланған.
Бірақ кеңістіктегі барынша қарапайым фигуралардың өзара
орналасуы мен бір – біріне қатысты байланысын өз бетінше анықтау
- студенттерге көптеген қиындықтар келтіреді.
Оқушылардың кеңістік жөніндегі түсініктерін дамытудың бірқатар
тәсілдері бар, солардың ең маңыздыларының бірі – стереометрия
есептерін шешу. Кеңістіктегі фигуралардың қасиеттерін есептер шешуге
қолдану болашақта мұғалім болатын студенттердің кеңістікті
қабылдауына мүмкіндік береді. Сырттай оқитын студенттерге
арналған стереометрия есептерін шешудің методикалық
нұсқауларында студенттер мен орта мектеп оқушыларына, мұғалімдеріне
қиындық келтіретін стереометрия есептерін шешудің мысалдары
келтірілген.
Бірінші тара у конструктивті геометрия есептері мен
кеңістіктегі түзулер және жызықтықты салуға арналған. Келесі
тарауларда көпжақтармтен олардың комбинациясы, айналудан пайда
болатын фигуралар туралы теориялық мәселелер келтіріліп,
есептер шешілген.
Оқырмандаға ұсынылып отырған методикалық нұсқаулар
оқушыларды кеңістіктегі негізгі геометриялық орындармен таоныстырады.
Сондай – ақ геометрялық орындарды стереометриялық есептерді шешуге
қалай қолданылатынын көрсетеді. Геометрияны үйрену барысында
оқырманның өзін қоршаған геометрияны көре білу дағдысымен қабілетін
дамытуы аса маңызды процесс болып табылады. Бізді қоршаған
көптеген заттар дөңгелек, тік төртбұрыш, цилиндр, конус, қиық конус
немесе шар формалары.
Айналамыздағы қоршаған геометриялық форма бізге күрделі не
өзінің табиғи формасын өзгерткен немесе әртүрлі
комбинациялы формада кездеседі.
Геометриялық фигуралар туралы абстрактілі ұғымдарды
оқырмандар көбінесе жай геометриялық денелердің моделі арқылы
оларды бақылап, күнделікті көріп және көз алдына елестетіп еске
түсіру арқылы қалыптастырады.

Кеңістіктегі түзулер мен жазықтықтар
І. Түзулер мен жызықтықтарды салу есептері
ІХ Х кластардағы стереометрия курсында оқушылар мен
педагогикалық институттардың студенттері көптеген қиыншылықтарға
кездеседі. Теоремалар мен олардың дәлелдеу жолдарын білгенімен де,
оларды пайдаланып есептер шешуде әр түрлі қиындықтар туады.
Көптеген озат мұғалімдердің іс – тәжірибесінде кездесетін кейбір
констлруктивті есептерді қарастыралық.
ІХ класс геометриясының алғашқы сабақтарында шешілетін
мұндай есептер оқушылардың кеңістік жөніндегі түсінігі молайтылды.
Конструктивті есептерді шешуге жаттыққан оқушылар стреометрия
есептерін өз бетінше шеше алады. Салу есептерін планиметрияда
әр түрлі сызба құралдарының көмегімен шешеді. Кеңістікте
жазықтықты немесе түзуді салуға көмектесетін сызу құралы жоқ.
Сондықтан кеңістікте конструктивтік геометрияны аксиома ретінде
аламыз. Кейбір қарапайым салулар мүмкін деп ұйғарылады да, басқа
күрделі салу жұмысы осыларға негізделеді. Төмендегі салулар
әрқашанда орындалады деп есептейміз.
І. Егер жазықтықты анықтайтын элементтер бір түзудің
бойында жатпайтын үш нүкте, түзу және одан тысқары жатқан
нүкте, қиысатын екі түзу, параллель екі түзу берілсе, онда
жазықтықты салуға болады; 2. Берілген немесе салынған екі
жазықтықты ң қиылыс у сызығын салуға болады; 3. Циркуль м ен
сызғыштың көмегімен орындауға болатын к ез келген салуды
әрбір жазықтықта орындауға болады.
Стерометрияда салулар ойша көз алдыға елестету арқылы
орындалады, шын мәніндегі кеңістік фигоураның кескіні
формелтді түрде тұрғызылады.
Бұл арада фигураның қаңқасы мен оның көрінбейтін
бөліктерін ажырата білу керек. Кеңістік фигурада проекцияланып
сызылатын қима жазықтықтардың көлеңкесінде қалатын ектіенші
рет көрінбейтін беттер мен сызықтар болады. Проекциялауды екі рет
қолданғанда үнемі үзік сызықтар қолдануға болмайды.
1- есеп. В нүктесі кубтың NK қырынан алынған. Ал, А нүктесі
FK қырында жатыр. АВ кесіндесінің созындысы мен кубтың MN, MF
қырларының созындылары қиылысатынын дәлелдеңдер.
Ав кесіндісі кубтың MNKF жағында жатыр. АВ кесіндісін екі
жағына да созсаң, осы жазықтықтағы MN, MF кесінділерінің
созындыларымен В1, В2 нүктелерінде қиылысады (1 - сурет)

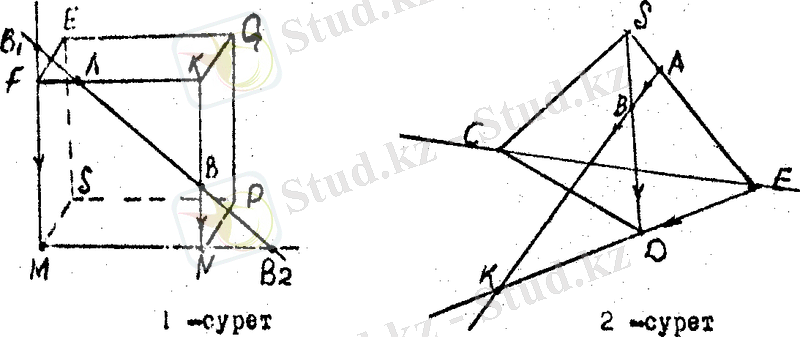
2 - есеп. Үшбұрышты пирпмиданың SE қырыны А1SD қырынан В нүктесі
алынған. АВ кесіндісінің созындысы мен пирпмида табанының
қиылысуы нүктесін салыңдар (2 - сурет)
S және А нүктесі арқылы түзу жүргізсек, ол С Е Д
табанымен Е – де қиылысады. Сол исяқты SB – ні созсақ. Д нүктесінде
қиылысады.
АВ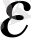(SDE) DE 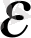(SDE) AB DE . Сондықтан бұлар К нүктесінде
қиылысады.
Пирамида сызбасының қасиеті бойынша SA1B1 жазықтықты басқа
кез келген жазықтықпен алмастыруға болады. Бұл жазықтықты A1B1 және SD
қабырғасынан алынған F нүктесі арқылы анықтабуға болады.

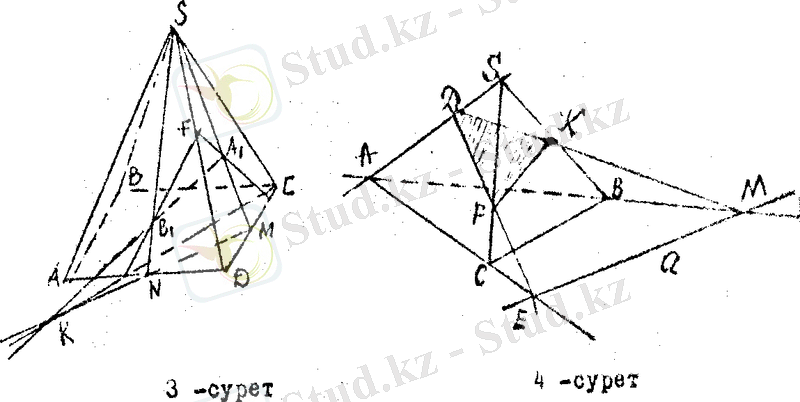
4 – есеп.
Үшбұрышты SABC пирамиданың SA қырында Д нүктесі және
пирамиданың табан жазықтығында жатқан а түзуі арқылы пирамидаға
қима жазықтық жүргізу керек (4 - сурет).
SAC және SAB бүйір жақтары табан жазықтығымен сәйкес АВ
және АМ кесінділері арқылы қиялысады, олай болса қима
жазықтық пен SAC жағының жазықтығы ДЕ түзуі арқылы қиылысады. Дәл
осы сияқты SAB жағының жазықтығы қима жазықтықпен ДМ түзуі
арқылы қиылысады.
ДЕ және ДМ түзулерін салу нәтижесінде FK нүктелерін саламыз.
Сонда АДFK қимасы шығады.
7 – есеп.
Тік параллепипедтің әр түрлі қырларында жатқан үш нүкте
арқылы қима жазықтық салу керек.
Мысалы: 7 – суретте көрсетілген бір дербес жағдайды
қарастыралық. Берілген нүктелерді бір табанына проекциялас ақ, 8
– суретте көрсетілгендей чертеж аламыз.

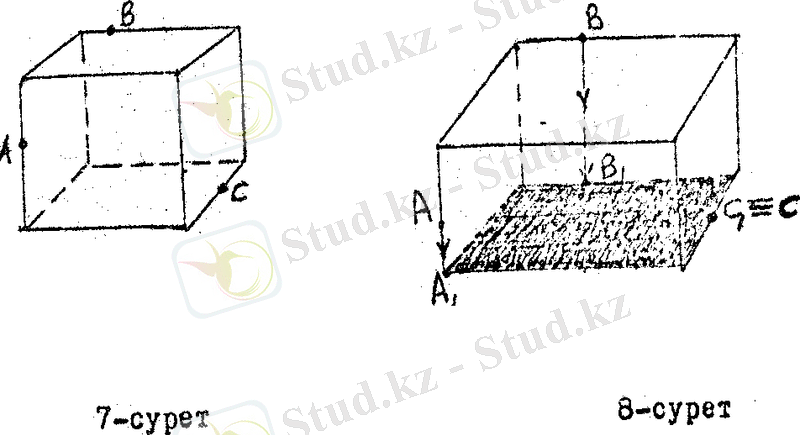
В мен А және В1 мен А1 сондай – ақ В мен С1 нүктелерін кесіндімен
қосамыз. А, В, В1А1 нүктелерін бастыра бір жазықтық салуға болады.
(9 - сурет). А1 В1 С1 - нүктелері жатқан жазықтық алғашқы АВВ1
жазықтығымен В1 А1 түзуінің бойымен қиылысады. Екі жазықтық
қиылысатындықтан ВА кесіндінің созындысы екі жазықтықтың қиылысуы
сызығымен бір Х1 нүктесінде қиылысады. Себебі АВ (А1 В1 С1) яғни РВ1
ара қашықтығы А1А ара қашықтығынан артық.Х1 ( А1 В1 С1)
болғандықтан Х1 нүктесімен С2 нүктесін қосуға болады. Ол
параллелпипедтің табанының қырынан Х2 нүктес інде қиылысады. АВС1
жазықтығы да аталған (АВВ1) және (А1 В1 С1) жазықтықтарымен Х1
нүктесінде қиылысатын көрсетуге болады. Себебі А1 В1 С1 Х2.

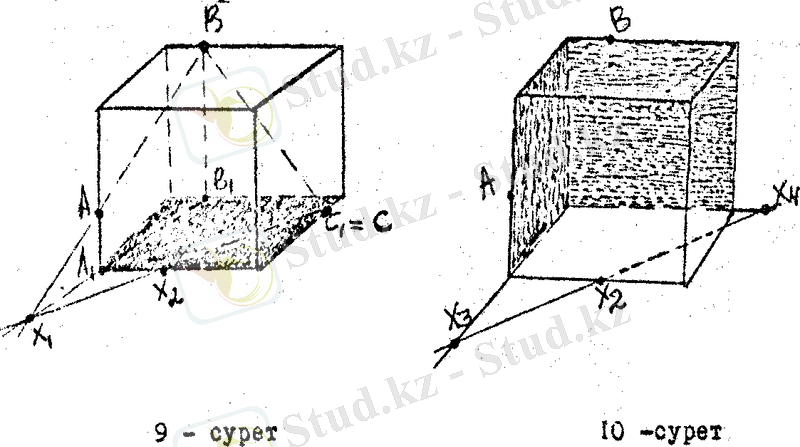
С1Х2 кесіндісін екі бағытта да созсақ, ол 10 – суретте
көрсетілгендей пареллелпипедтің табанындағы қалған екі қабырғаның
созындысымен Х3 Х4 нүктелерінде қиялысады. Х4 нүктесін В
нүктесімен қоссақ, 11 – суретте көрсетілгендей ол параллелпипед
қырымен Х5 нүктеде қиылысады. Х4 Х5 нүктелері параллелпипедтің Б
В1 нүктелері жатқан жазықтықта жатыр. Дәл осы сияқты Х3 А
кесіндісін созсақ, параллелпипедті ң жоғарғы табанының бір қырымен Х6
нүктеде қиылысады Х3 АХ6 нүктелері А,А1 нүктелері жатқан жазықтықта
жатыр (11 - сурет).

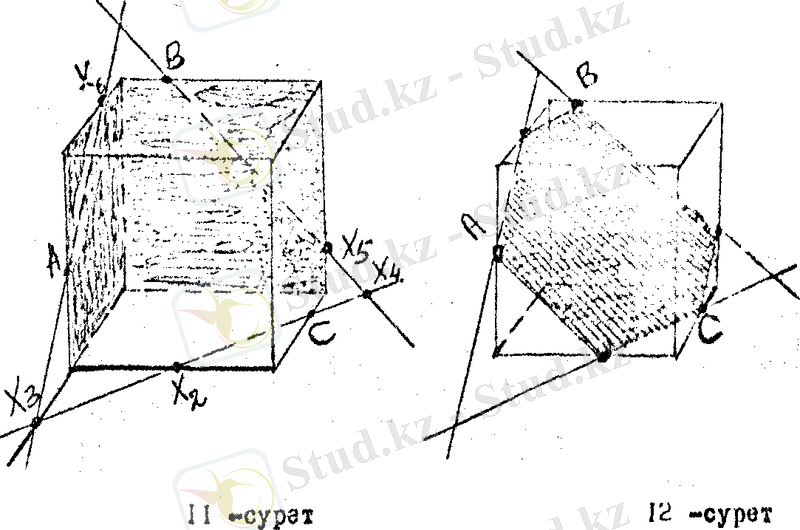
Табылған нүктелерді қоссақ берілген А,В,С нүктелерінен өтетін
қима жазықтық шығады (12 - сурет).
8 – есеп.
Үшбұрышты призма берілген. А,В нүктелері 13 – суретте
көрсетілгендей призманың әр түрлі жақтарында және С нүктесі
призманың бір табанының қырында жатыр. Осы үш нүктеден өтетін
қима жазықтық салу керек.
Салуы А,В,С нүктелерін призма табанына проекциялап (14 -
сурет) А1 В1 нүктелерін қосамыз. АВ мен А1 В1 кесінділерінің
созындылары (1 – есептегі сияқты) Д нүктесінде қиылысады.

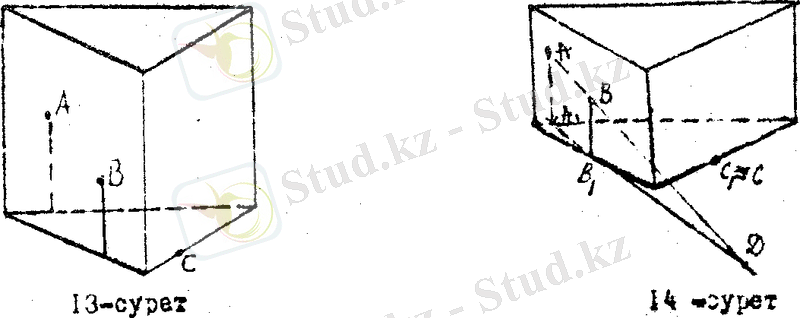
Табылған Д нүктесін С1 мен қосып, одан әрі созсақ, ол призма
тобының (15 - сурет) А1 нүктесі жақтан қабырғасымен Х2 нүктесінде
қиылысады. Х2 нүктес ін А нүктесімен қосып, одан әрі созсақ, ол
призма қарқымен Х3 нүктесінде қиылысады, себебі бұл қыр да А
нүктесі жатқан жазықтықта жатыр.

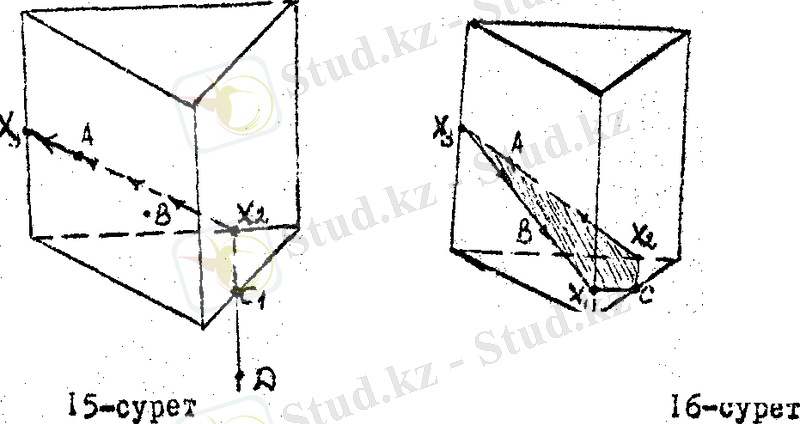
Х3 нүктесі жатқан қыр А және В нүктелері жатқан
жазықтықтардың қиылысу сызығы, сондықтан Х3 нүктесін В нүктесімен
қосуға болады. Х3 В – ні созсақ, ол призма қырымен (16 - сурет) Х2
нүктесінде қиылысады. Х1 мен С нүктелерін қосуға болады. Сонымен Х1 СХ2
А Х3 В – ізделінді қима жазықтық.
9 –есеп.
А,В нүктелері SMNP үш пирамиданың бүйірі жақтарында, ал С нүктесі
табан жағында жатыр. Осы үш нүктеден өтетін пирамиданың бір
параллель қима жазықтық жүргізу керек.
Салуы: S нүктесін А,В нүктелерімен қосып, одан әрі созсьақ,
олар табанның қабырғаларымен сәйкес А1 В1 нүктелерінде қиылысады. М
нүктесін С нүктес імен қосуға болады. (17 - сурет). А,В нүктелерін
қосып, одан әрі созсбақ және МNР табанындағы А1 В1 нүктелерін
қоысып, одан әрі созсақ, бұлар Х1 нүктесінде қиылысады (18 - сурет).
Яғни АА1 В1 В – бір жазықтықты анықтайды. Пирамиданың табанында жатқан
С1 нүктесін Х1 мен қоссақ, ол NP және МР қабырғалары мен сәйкес Х2 , Х3
нүктелерінде қиылысады (19 - сурет).

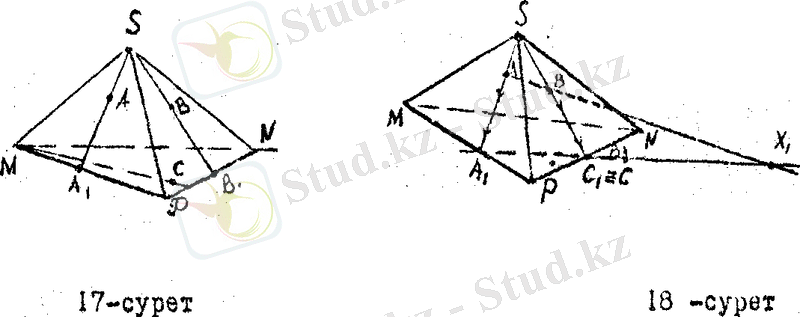
20 – суреттегідей Х1, Х3 нүктелерін сәйкес В,А нүктелерімтен қосып,
одан әрі созсақ, олар NS, MS қырлармен сәйкес Х4 , Х5 нүктелерде
қиылысады. Х4 , Х5 нүктелерді қоссақ ізделінеді қима жазықтық шығады.
Бұл жазықтықтың SP қырына паралледь екенін дәлелдеуді оқырмандарға
қалдырамыз. (21 - сурет)

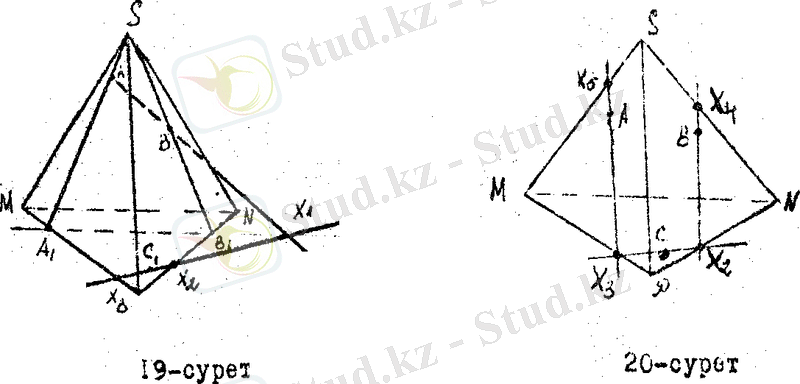
10 – есеп.
S ABK үш бұрышты пирамиданың (SAK) және (SBK) бүйір жақтарынан
сәйкес С және Д нүктелері берілген. Осы нүктелерден өтетін SK қырына
параллель қима жазықтық салу керек (22 - сурет).

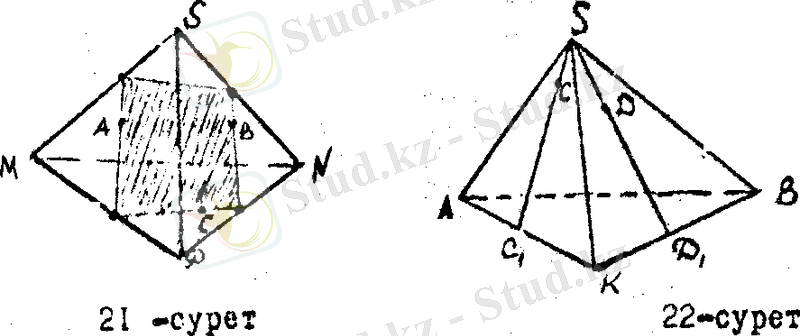
Салуы: СД және С1 Д1 кесінділерінің созындысы Х1 нүктеде қиылыс
ады (Алдынғы есептерді қарау керек). Табылған Х1 нүктесінен АВ – ға
паралледь түзу жүргізсек, ол пирамида табанының ВК, КА қабырғаларымен
(23 - сурет) сәйкес Х2 және Х3 нүктелерінде қиылысады.

Х3 пен С, Х2 Д нүктелерін қосып, одан әрі созсақ, олар пирамиданың
AS, BS қырларымен қиылысады. Табылған барлық нүктелерді қоссақ 24 –
суретте көрсетілгендей қима жазықтық шығады.

11 – есеп.
АВСД үшбұрышты пирамиданың АДС бүйір жағына параллель
пирамида биіктігінің бойында жатқан М нүктесінен өтетін қима
жазықтық салу керек. (25 - сурет)
Салу; А және М нүктелерін қосып, одан әрі созсақ, ол ВДС
жазықтығымен А1 нүктесінде қиылысады. В,А1 нүктелерін қосып, әрі
қарай созсақ, ол ДС қабырғасымен В1 нүктесінде қиылысады.

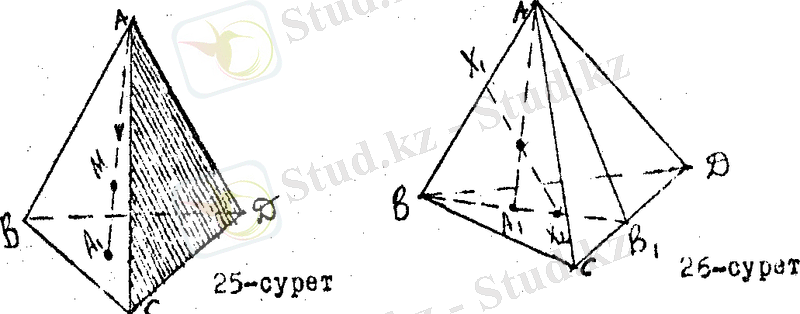
АДС бүйір жағындағы АВ1 нүктелерін кесіндімен қосуға болады. (26 -
сурет). М нүктесінен өтіп, АВ2 –ге параллель болатын түзу
жүргізсек, ол ВВ1 мен Х2 , АВ мен Х2 нүктесінде қиылысады.
Пирамида табанындағы ДС қабырғасына параллель болып Х2 нүктесінен
өтетін түзу жүргізсек, ол ВС, ВД қабырғаларымен сәйкес Х3, Х4
нүктелерде қиылысады. (27 - сурет).

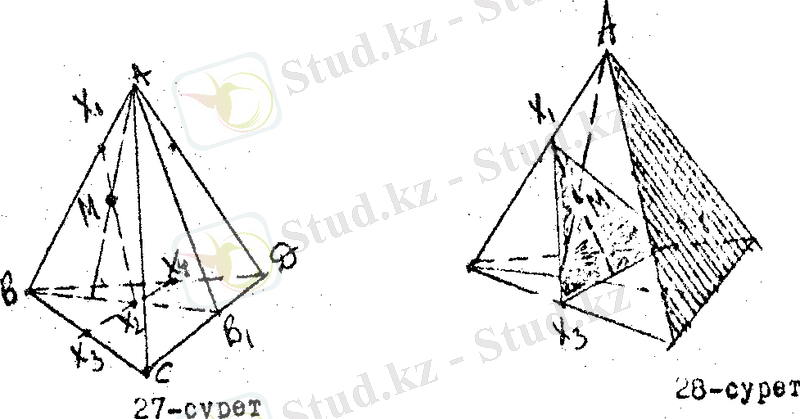
Х3, Х4, Х1 нүктелері бір жазықтықты анықтайды. Бұл
жазықтықтағы Х1, Х2 – нің бойында М нүктесі жатады. Х3, Х4, Х1 -
ізделінді қима (28 - сурет).
12 – есеп.
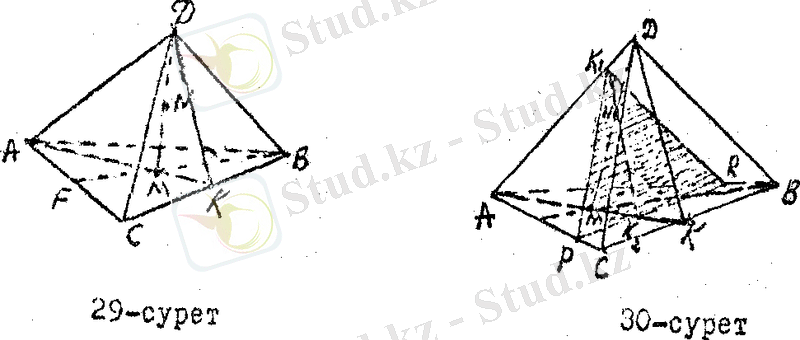АВСД тетраэдрдің Д төбесі АВС жағының медианаларының қиялысу
нүктесімен қосылған. ВСД жағына пареллель және ДМ кесіндісінің
бойындағы N нүктесінен өтетін қима жазықтық салу керек (29 - сурет).

Салу: АВС үшбұрышының медианаларының бірі – АК, ал олардың қиылысу
нүктесі – М болсын. АК,АД, ДК – арқылы қима жазықтық саламыз. Сонда есеп
шартында берілген N 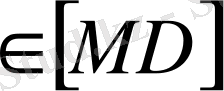нүктесі арқылы ВС – ға паралледь түзу жүргізсек,
ол АС,АВ қабырғаларымен сәйкес P және R нүктелерінде қиылысады. К1 мен Р
және R нүктелерін қосып ізделінеді РRK1 жазықтығын аламыз (30 - сурет).
Бұл жазықтық есеп шартын қанағаттандырады. Өйткені

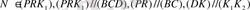
13 – есеп
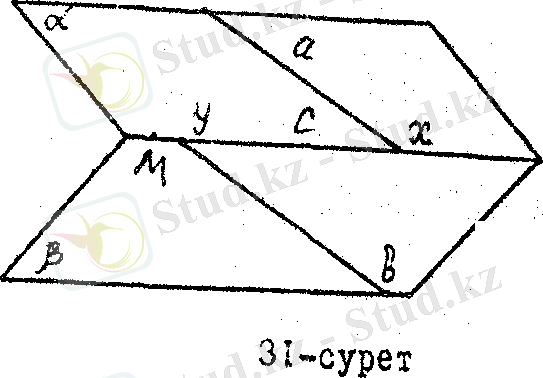
Берілген М нүктесі арқылы а,в айқас екі түзуді қиятын түзу
жүргізу керек,
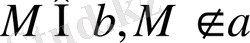
Талдау. С – ізделінді түзу болсын, онда қиылысатын а және
с түзулері өздері арқылы өтетін жазықтығын, ал в және с
түзулері өздерінен өтетін 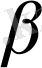жазықтығын анықтайды. MC =
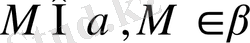болатындықтан (31 - сурет).
Егер, есептің шешімі бар болса, онда ізделінді түзу
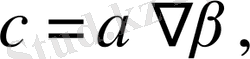мұндағы
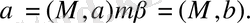
Бұдан, мынадай салу шығады:
1. а түзуі М нүктесі арқылы жазықтығын;
2. в түзуімен М нүктесі арқылы 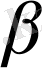жазықтығы;
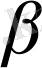3. мен жазықтықтарының қиылысу сызығы с түзуін
саламыз.
Егер с түзуі а және в түзулерін қиып өтсе, онда ол –
ізделінеді түзу.
31 – суретте с түзуі а және в түзулерін Х және У нүктелерінде
қияды.
Зерттеу. Егер есептің шешімі бар болса, онда ізделінді түзу
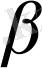және жазықтықтарының қиылысу сызығы екендігі талдау
кезінде көрсетілген. Себебі а және в айқас түзулер және М 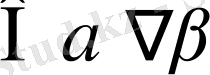, онда
және 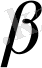әртүрлі жазықтықтар және бұлардың қиылысу сызығы –
түзу. Бұдан есептің бір ғана шешімі бар екендігі шығады. Сондай
–ақ ас немесе вс болуы да мүмкін. Бұл жағдайларда есептің
шешімі жоқ.
Өзіңізді тексеру үшін мына сұрақтарға жауап беріңіз?
1. Есептің бір ғана шешімі бар екені қайдан шығады?
2. Қандай шарт орындалғанда, есептің шешімі бар болады?
3. түзуінің әрқашан бар екеніне қарамастан есептің шешімі
болмауы мүмкін бе?
Үлгі ретінде бірінші сұраққа жауап берелік. Ізделінді түзу
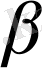мен жазықтықтарының қиылысу сызығы болатыны айтылған. Бұд
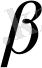ізделінді түзуді тек мен жазықтықтарының көмегімен салуға
болады деген сөз емес. Керісінше , 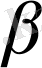жазықтықтарының
қиылысу сызығынан өзгеше кез келген түзу есептің шешімі бола
алмайтынын көрсетеді. , 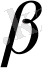жазықтықтары беттесе алмайды,
себебі а және в түзулері бір жазықтықта жатпайды. Сонымен бірге
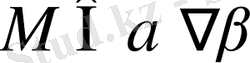ендеше, қиылысуы түзу болады.
14 – есеп.
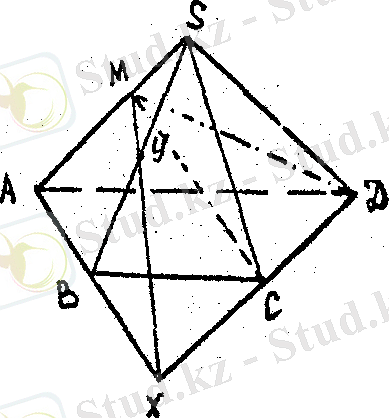SABCD пирамидасы және оның SA қырында жататын М нүктесі
берілген. М нүктесінен өтетін және SB және СД түзулерін қиятын түзу
жүргізу керек. (32 - сурет).

13 – мысалдың шешуінде көрсетілгендей ізделінеді түзу = (MSB)
және 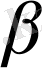=(MSD) жазықтықтарының қиылысу сызығы болуы мүмкін. Мұны
салу үшін СД түзуі мен =(MSВ) жазықтығының қиылысу нүктесін
салу жеткілікті.
Салу. 1) ізделінді Х нүктесін АВ және СД түзулерінің
қиылысу нүктесі ретінде немесе СД түзуі мен (MSB)
жазықтығының қиылысуы ретінде саламыз:
2) М және Х нүктелерін қосамыз. Егер АВ мен СД түзулері
қиылысса, онда ізделінді МХ түзуі мен 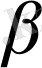жазықтықтарының
қиылысу сызығы болады (32 – сурет). Егер АВ мен СД түзулері
параллель болса, онда есептің шешімі болма йды.
Бұл есептің шешімі 13 – есептің басқа бір жалпы шешімін
табуға мүмкіндік береді.
М нүктесі мен а түзуі арқылы жазықтығын салуға
болады. Бұдан соң в түзуі мен жазықтығының Х қиылысу нүктесін
саламыз.
Егер МХ түзуі а түзуін қиятын болса, онда бұл МХ түзуі
есептің шешуі болады. Х нүктесін салу үшін в түзуі арқылы үшінші
бір 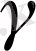жазықтығын жүргізу жеткілікті. 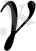және жазықтығының
қиылысу сызығы түзуін және Х = нүктесін салуғаболады. 13 –
есепте а = (SB), = (CD), = (MSB), 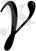= (ABSD), = AB,
мен жапзықтығының қиылысу сызығы С мен МХ түзуі
беттесетінін байқау қиын емес. 13 – 14 есептердің шешулерінде қандай
айырмашылық бар екеніне назар аударалық. 31 – суреттегі а,в,с түзулері
қалауымыз бойынша алынған. Ал, 32 – суреттегі түзулер қалауымыз
бойынша алынбайды, түзулер есеп шартына сай жүргізіледі, МХ түзуі
мен Х нүктесі есептің шартын анықтағанда салуларды орындауға
болады.

ІІ Тарау. КӨПЖАҚТАР
Геометриялық фигуралардың бар баолуын зерттеу есептері
Геометрия есептерін шешкенде оның шартын талдау ең негізгі
мәселе болып табылады. Есептің шешуі ретінде табылған формулалар
әпқашан есептің жауабы ретінде алына бермейді.
1 – есеп.
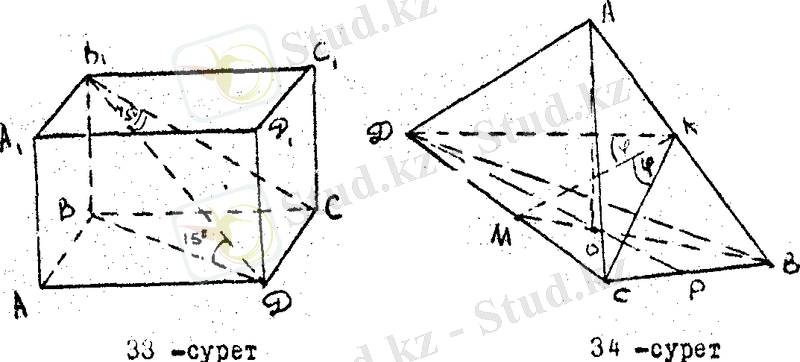
Тік төрт бұрышты параллелепипедтің диагоналының ұзындығы - ға
тең. Ол табан жазықтығымен 150, ал үлкен бүйір жағымен 450 бұрыш
жасайды. Параллелепипедтің көлемін табыңдар (33 - сурет).
Тік төртбұрышты параллелепипедтің көлемінің формуласы
бойынша 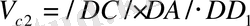(1) деп жазуға болады. ВВ1 ВС, ВС СД екенін ескерсек,
үш перпендикуляр туралы теорема бойынша ВС болады, сондықтан
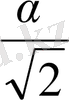ДС = BDsin DBC = sin 450 = ; (2)
Есеп шарты бойынша ДД1 = BB1 және BDB1 = 150 , онда ДД1 =
sin 150 (3).
Пифагор теоремасы боынша
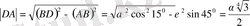(4).
(2), (3), (4) теңдіктерді ескеріп көлемді табамыз:

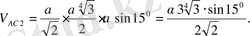
Зерттеу. ВДВ1 = , DBC = 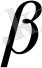Есеп шарты бойынша 0,

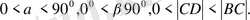
а) В1 ВСД – тетраздардың көмекші фигура ретінде бөліп
қарастырамыз;
б) ВД 0, 0B1 DB900 және 0DB1c 900 шарттарынан В1 ДВ және В1ДС
тікбұрышты үшбұрыштарының бар болатыны шығады. Бұлардан келіп ВСД
тікбұрышты үшбұрыштарының бар болатыны шығады. Айтылғандарға
сүйеніп В1ВДС тетраэдрының бар болатындығына көз жеткіземіз.
Геометрияның анрайы аксиомаларына негізделіп, бір ғана СДА = 90 0
және ДА = СВ шарттары орындалғанда, параллелепипедтің А төбесін
салуға болатыны шығады. Бұл әрі ВА және ВВ1 түзулері арқылы
анықталатын бір ғана жазықтық жүргізуге болады.
в) тетраэдрдың бар болу облысы 0CDBCB1D түрінде болады;
г) СД, ВС, В1Д кесінділерінің ұзындығын арқылы өрнектесек,
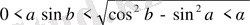шығады. Есеп шартын ескеріп, соңғы алынған теңсіздіктер
системасын шашсек,
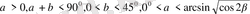
Берілген шарт 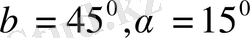үшін соңғы екі теңсіздік орындалмайтынын
байқаймыз, сондықтан есептің шешімі болмайды. Есеп шешуге көмекші
геометриялық фигураны пайдалану геометриялық есептерді зарттеу
жұмысын жеңілдетуге мүмкіндік береді. Бұл геометриялық фигураларда
болмайтын (сандық көмекші мәні ізделетін) элементтерге байлансыт
пайда болатын қателіктердің сипатын анықтауға мүмкіндік береді.

2 – есеп.
Дұрыс үш бұрышты АВСД пирамиданың бүйір қыры в- ге, ал бүйір
жақтарының арасындағы бұрыш 2 - ге тең. Пирамиданың табынындағы
қырлардың ұзынд2ығын табыңыз (34 - сурет).
Зерттеу. Біздің мақсатымыз есепті зерттеу болғандықтан оның
шешімін бірден жазалық, ізделінді ұзындық 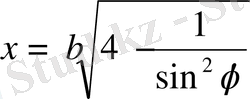Бұл арадан
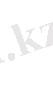
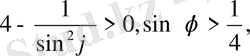есеп шарты бойынша 2 бұрышы 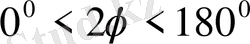аралығында жатады.
Сондықтан 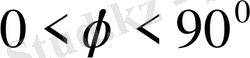және .
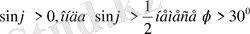Жоғарыда келтірілген мысал есептерден төмендегідей қорытындыға
келеміз. Егер есептің сызбасы бола алатын ең болмағанда бір
геометриялық фигүура бар болса, онда ос ы фигураға сәйкес
есептің шешімі бар болады. Керісінше жағдаюйда есептің
шешімі болмайды. Есеп шешуге қажетті бірінші ұғымдары
қарастырылады.
1 – анықтама. Егер папаметрлердің берілген мәндерінде есепті
аксиоматикалық жолмен шешу мүмкіндігі дәлелденген болса, онда
параметрлердің мәндері үшін геометриялық фигура анықталған деп
аталады.
Аксиоматик алық салу деп – салу аспаптарының көмегінсіз
геометриялық аксиомаларына негізделіп салуды айтады. Геометрияның
көптеген есептері салу аспаптарына тәуелсіз болады,
фигураның бар болуын дәлелдеу жұмысы аксиометрияға негізделеді.
2 – анықтама. Е геометриялық фигура бар болғандай есеп
шыртындағы параметрдың мәндерінің жиынын оның мүмкін мәндірі
деп аталады. Әрқашан да бар болатын нақты объектілердің
эелменттері оң мәндер қабылдабйтын кейбір шектеулер есеп
шартына сай болуы керек.
Әрқашан да бар болатын геометриялық фигура жөніндегі
қажетті, жеткілікті шарттар мен қажетті және жеткілікті шарттардың
айырмашылығы бар. Геометриялық фигура үшін қажетті шарт
дегеніміз әрқашан орындалатын, берілген фигура туралы есептің
шешімі бар болатындай орындалатын, берілген фигура туралы есептің
шешімі бар болатындай шарттар. Қажетті шарттрадың бірі
орындалмаған жағдаюйда есептің шешімі болмайды. Керісінше,
тұжырымда дұрыс болмайды. Мысалы, қабырғалары 5 см, 7 см, а см үшбұрыш
бар болуының ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.