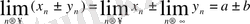Сан тізбектері: жинақталу, шек және оның қасиеттері, Коши критерийі мен Больцано-Вейерштрасс теоремасы


Сан тізбегі. Жинақты және жинақсыз тізбектер. Тізбектің шегі және оның қасиеттері. Коши критериі. Монотондық тізбектердің шектері. Тізбектің жоғары және төменгі шектері. Больцано-Вейерштрасс теоремасы. Шексіз аз және шексіз үлкен тізбектер. е саны
Сан тізбегінің ұғымы . Шексіз сандар жиынын қарастырайық.
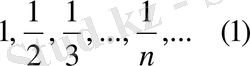
Осы сандар жиынын натурал сандар жиынмен сәйкестіріп, әрбір натурал санға бір санды сәйкес қойып реттесек, онда біздің жиын реттеледі, яғни 1 -ші орында 1, 2-ші орында 1/2, 3-ші орында 1/3 деп осылай реттелсе, онда оны реттелген жиын дейді. Натурал сандар мен нөмерленіп реттелген сандар жиынын сан тізбегі дейді. Жиындағы сандар саны ақырлы болса, онда (жиынды) тізбекті ақырлы, ал саны ақырсыз болса, онда тізбекті ақырсыз дейді. Жалпы жағдайда тізбек былай кіші әріптермен белгіленіп беріледі.
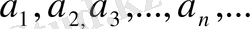 (2)
(2)
Тізбектегі әрбір сан тізбектің мүшесі делінеді.
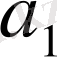 - 1-ші мүше,
- 1-ші мүше,
 - 2-ші мүше ……
- 2-ші мүше ……
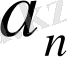 - n -ші мүше.
- n -ші мүше.
Мысал.
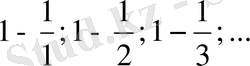 жалпы мүшесі
жалпы мүшесі
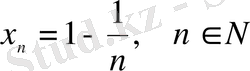 формуламен берілетін сан тізбегін қарастырайық. Бұл тізбек 0 және 1 сандармен шектелетінін дәлелдеу қиынға соқпайды, және ол бірсарынды өспелі. Тізбектің нөмері өскен сайын ол 1 санына жақындай береді. Сонда мына
формуламен берілетін сан тізбегін қарастырайық. Бұл тізбек 0 және 1 сандармен шектелетінін дәлелдеу қиынға соқпайды, және ол бірсарынды өспелі. Тізбектің нөмері өскен сайын ол 1 санына жақындай береді. Сонда мына
 айырманы қарастырайық.
n
-
өсуіне бұл айырма кішірейе береді. Мысалы,
n
=11 болса
айырманы қарастырайық.
n
-
өсуіне бұл айырма кішірейе береді. Мысалы,
n
=11 болса
 айырма 0, 1 - ден кіші, ал
n
=101 тең болса, онда 0, 01 кіші, осылай кеми береді. Сонда біз бір кез келген оң кіші ε санын алып, ол үшін
N(ε)
нөмері табылып, барлық
айырма 0, 1 - ден кіші, ал
n
=101 тең болса, онда 0, 01 кіші, осылай кеми береді. Сонда біз бір кез келген оң кіші ε санын алып, ол үшін
N(ε)
нөмері табылып, барлық
 үлкен болғанда
үлкен болғанда
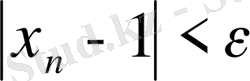 теңсіздігі орындалады, яғни {
Xn
}тізбегінің барлық мүшелері (
1-ε, 1+ε
) аралығында жатады. Бұл деген 1 саны {
Xn
} тізбегінің шегі дейді, және былай белгіленеді:
теңсіздігі орындалады, яғни {
Xn
}тізбегінің барлық мүшелері (
1-ε, 1+ε
) аралығында жатады. Бұл деген 1 саны {
Xn
} тізбегінің шегі дейді, және былай белгіленеді:
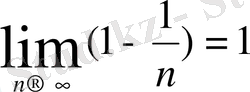
Тізбектердің берілу тәсілдері.
Тізбекті берілді дейді егер оның мүшелері белгілі болса. Сонда тізбектерді 1) аналитикалық, 2) реккуренттік, 3) тізім тәсілдерімен беруге болады.
1) Аналитикалық тәсіл . Бұл жағдайда тізбектің n - ші мүшесінің формуласы беріледі.
Мысалы:
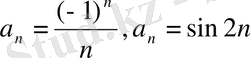 осыдан
осыдан
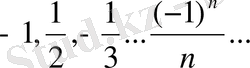 ;
sin0, sin4, sin6, …, sin24…
шығады.
;
sin0, sin4, sin6, …, sin24…
шығады.
2) Реккуренттік тәсіл . Тізбек мүшелері өзара реккуренттік байланыспен беріледі.
Мысалы:
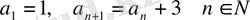 , сонда
, сонда

1, 4, 7, …. ,
 шығады.
шығады.
Тізбектің жинақтылығының қажетті шарты.
Тізбек {
Xn
} - жинақты болып,
 саны шегі болса, яғни
саны шегі болса, яғни
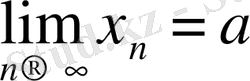 .
.
Онда шектің анықтамасынан, кез - келген оң кіші
ε
саны үшін
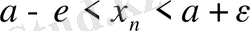 теңсіздігі орындалады. Бұл дегеніміз
теңсіздігі орындалады. Бұл дегеніміз
 десек
десек
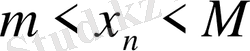 теңсіздігі орындалады, олай болса {
Xn
} тізбегі шенелген тізбек болады.
теңсіздігі орындалады, олай болса {
Xn
} тізбегі шенелген тізбек болады.
Тізбек жинақты болу үшін, оның шенелген болуы қажетті.
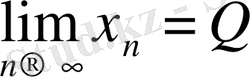
Тізбек шектері туралы теоремалар.
- Тізбек екі әртүрлі шекке жинақтала алмайды. (шектің жалғыздығы туралы теорема)
- Мүшелер шамасы өзара тең болатын тізбектің шегі, сол шамаға тең.
- Егер {Xn} тізбегі бір- санына жинақталса жәнеболса, онда оның барлық мүшелерінің шамасыp- дан үлкен (q- ден кіші) болады.
- Егер {Xn} тізбектің шегі бар болса, онда ол шектелген болады.
- Егер {Xn} жәнетізбектерінің шегі бар болса, онда олардың қосындысы мен айырмасының да шегі бар болады.
6) Егер { Xn } және {Yn} тізбектерінің шегі бар болса, онда олардың көбейтіндісініңде шегі бар болады.
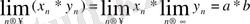
7) Егер {
Xn
} және {
Yn
} тізбектерінің шегі бар және
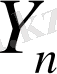 ≠0 болса, онда олардың
≠0 болса, онда олардың
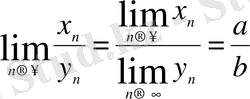
қатынастарының да шегі бар болады.
Тізбектің шегі ұғымының геометриялық мағынасы:
Бұл мақсатта сандар осін алып, айнымалы х n -нің мәндерін және а - ε мен а + ε сандарын нүктелермен кескінделік.

n-нің N-нен үлкен барлық мәндері үшін (3) теңсіздіктер орындалатын болғандықтан х
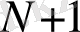 нүктесінен бастап барлық х
n
нүктелері (а - ε, а + ε) интервалының (бұл интервалдың ұзындығы 2ε, центрі а нүктесі) бойында болады. Бұл интервалдың сыртында айнымалы х
n
-нің санаулы мүшелері ғана қалады.
нүктесінен бастап барлық х
n
нүктелері (а - ε, а + ε) интервалының (бұл интервалдың ұзындығы 2ε, центрі а нүктесі) бойында болады. Бұл интервалдың сыртында айнымалы х
n
-нің санаулы мүшелері ғана қалады.
Егер а саны айнымалы х n -нің шегі болса, өзгерту процесінде айнымалы өзінің шегі а-ға мейлінше жақындайтыны (2) теңсіздіктен көрінеді. Айнымалы х n -нің а санына жақындауының үш түрі болуы мүмкін:
1. Айнымалы х n өзіңің шегі а-ға онан үнемі кіші бола отырып ұмтылады, яғни х n а-ға
Мысалы:
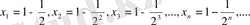
тізбегінің шегі 1, бірақ тізбек мүшелерінің бәрі де 1-ден кіші.
Ш ы н ы н д а: кез келген аз сан ε>0 берілген делік. Біздің максатымыз: берілген ε>0 үшін N саны табылып, n>N теңсіздігін қанағаттандыратын барлық n үшін
х n -1I < ε (4)
Яғни

теңсіздігінің орындалатындығын көрсету. Бұл теңсіздік орындалады десек,

болар еді.
 (5)
(5)
Демек, (5) теңсіздік орындалса ғана, (4) теңсіздік орындалады. Олай болса, N нөмірі үшін
 -ні алуға болады,
-ні алуға болады,
яғни: N
=
Е
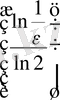 .
Егер Е
.
Егер Е
 < 0 болса,
N=1
деп аламыз. Сөйтіп, бұл сан тізбегінің шегі а=1. Сонымен қатар
< 0 болса,
N=1
деп аламыз. Сөйтіп, бұл сан тізбегінің шегі а=1. Сонымен қатар
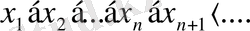
болғандықтан, тізбек 1-ге өсе ұмтылады .
x 1 x 2 x 3 x 4
0
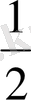


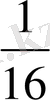 1
1
Чертёжден х 1 -нің (0, 1) интервалының орта нүктесі, х 2 -нің (х 1 , 1) интервалының орта нүктесі. х 3 -нің (х 2 , 1) интервалының орта нүктесі, . . . , x n -нің (х n-1 , 1) интервалының орта нүктесі екенін көреміз. Сонымен бірге х 1 , х 2 , х 3 , . . . , х n , . . . нүктелері n өскен сайын a= 1 нүктесінің сол жақ маңына қоюлана түсетіндігін байқаймыз.
2) Айнымалы
 өзінің шегі а-ға үнемі онан үлкен бола отырып ұмтылады, яғни а-ға бара ұмтылады, яғни
өзінің шегі а-ға үнемі онан үлкен бола отырып ұмтылады, яғни а-ға бара ұмтылады, яғни
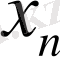 а-ға кеми бара ұмтылады.
а-ға кеми бара ұмтылады.
Мысал:
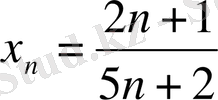 түрінде берілген сан тізбегі өзінің шегі
түрінде берілген сан тізбегі өзінің шегі
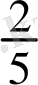 ге кеми бере ұмтылады.
ге кеми бере ұмтылады.
Шешуі:
 >0
>0

Айнымалы
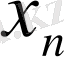 өзінің шегі а-ға үнемі онан үлкен бола отырып ұмтылады, яғни
өзінің шегі а-ға үнемі онан үлкен бола отырып ұмтылады, яғни
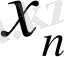 а-ға кеми бара ұмтылады.
а-ға кеми бара ұмтылады.
Мысал :
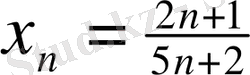 түрінде берілген сан тізбегі өзінің шегі
түрінде берілген сан тізбегі өзінің шегі
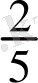 ге кеми бара ұмтылады.
ге кеми бара ұмтылады.
Шешуі:
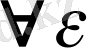 >0
>0
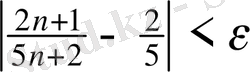 теңсіздігі N нөмірінің қай мәніне бастап орындалатынын анықтаймыз.
теңсіздігі N нөмірінің қай мәніне бастап орындалатынын анықтаймыз.
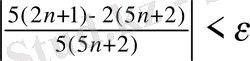
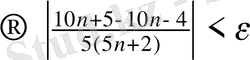
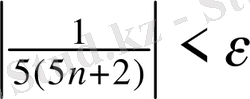

 ,
,
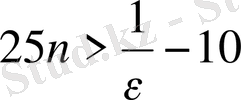 ,
,
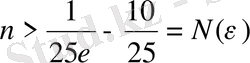
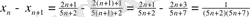 >0
>0
Демек n өссе қарастырылып отырған тізбектің мүшелері кемиді. Бұдан тізбек өзінің шегі
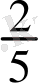 ке кеми бара ұмтылатынын көреміз.
ке кеми бара ұмтылатынын көреміз.
Салдарлар:
- Ақырсыз кішкене мен тұрақтының көбейтіндісі ақырсыз кішкене шама болады.
- Кез келген ақырсыз кішкене - шекара қойылған айнымалы, сонымен бірнеше ақырсыз кішкенелердің көбейтіндісі де ақырсыз кішкене болады.
- Ақырсыз кішкенелердің кез келген оң бүтін дәрежесі де ақырсыз кішкене шама болады.
- Ақырсыз мен арқылы текке ұмтылатын айнымалының ақырсыз кішкене болады.
... жалғасы3. Ақырсыз үлкен шамалар және олардың ақырсыз кішкенелерімен байланысы.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz