Регрессиялық талдау: статистикалық тәуелділік, жалпы және қос сызықтық регрессиялық модельдер; Гаусс-Марков теоремасы және детерминация коэффициенті


7-Лекция. Регрессиялық талдау
Жоспары:
7. 1. Регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер) .
7. 2. Қос сызықтық регрессия.
7. 3. Регрессия теңдеуінің сапасын тексеру (Гаусс-Марков теоремасы және детерминация коэффициенті) .
Мақсаты:
Кез келген экономикалық көрсеткішке бір ғана емес, көбінесе бірнеше факторлар әсер етеді. Мысалы, кейбір тауварға сұраныс тауар бағасымен ғана емес, басқа оны алмастыратын және толықтыратын тауарлармен, тұтынушы табысымен және көптеген басқа факторлармен анықталады. Бұл жағдайда екі айнымалының сызықтық регрессиясының заңды жалғасы - регрессия моделі қарастырылады. Яғни, регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер) және моделде
 кездейсоқ фактор болу себептерін, қос сызықтық регрессия және регрессия теңдеуінің сапасын тексерудегі Гаусс-Марков шарттарын және детерминация коэффициентін, сызықтық регрессиялық талдау есебін және ең кіші квадраттар әдісін түсініп, есептер шығарып, жаттығулар жасау.
кездейсоқ фактор болу себептерін, қос сызықтық регрессия және регрессия теңдеуінің сапасын тексерудегі Гаусс-Марков шарттарын және детерминация коэффициентін, сызықтық регрессиялық талдау есебін және ең кіші квадраттар әдісін түсініп, есептер шығарып, жаттығулар жасау.
Тақырып бойынша негізгі ұғымдар: Регрессия, регрессиялық талдау, регрессиялық модель, кездейсоқ фактор, қос сызықтық регрессия, регрессия теңдеуі, көптік сызықтық регрессия, регрессия теңдеуінің сапасын тексеру, статистикалық тәуелділік, Гаусс-Марков теоремасы, детерминация коэффициенті, ең кіші квадраттар әдісі және ең кіші квадраттар әдісінің алғы шарттары, сызықтық регрессия теңдеуінің коэффициенттерінің интервалдық бағасы.
Регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер) . Экономика жеке ғылым болып қалыптасқаннан бері зерттеушілер экономикалық дамудың болжамдарын көрсету арқылы экономикалық жағдайларға ықпал етуге тырысты. Бір түрлі экономикалық жағдай дәл солай екінші рет қайталанбайды деп айтуға болады, себебі бір шартта екі стратегияны қолдану мүмкін емес. Сондықтан экономикалық талдаудың негізгі міндеттерінің бірі экономикалық объектінің дамуын болжау.
Кез келген экономикалық көрсеткіш көптеген факторларға тәуелді. Экономикалық модель құруда олардың бәрін қамту мүмкін емес. Әдетте зерттелініп отырған экономикалық көрсеткішке нақты әсер ететін шектелген факторлар алынады, ал ескерілмеген факторлар экономикалық көрсеткіштерге ауытқулар енгізбейді. Нақты ғылымдарда көбіне функционалдық тәуелділік қарастырылады, яғни тәуелсіз айнымалының бір мәніне тәуелді айнымалының бір мәні сәйкес болады. Экономикалық айнымалылар арасында ондай тәуелділік жоқ.
Мысалы: кіріс пен тұтыну арасында, баға мен сұраныс арасында, еңбек өнімділігі және жұмыс стажы арасында қатал тәуелділік жоқ. </h4>
Статистикалық тәуелділік
Анықтама 1
Егер
 кездейсоқ шамасының әрбір мүмкін мәніне
кездейсоқ шамасының әрбір мүмкін мәніне
 кездейсоқ шамасының мүмкін мәндерінің жиыны, яғни статистикалық үлестіруі сәйкес болса, онда мұндай тәуелділік статистикалық тәуелділік деп аталады.
кездейсоқ шамасының мүмкін мәндерінің жиыны, яғни статистикалық үлестіруі сәйкес болса, онда мұндай тәуелділік статистикалық тәуелділік деп аталады.
Анықтама 2
 кездейсоқ шамасының
кездейсоқ шамасының
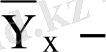 шартты орташа мәні деп
шартты орташа мәні деп
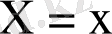 болғандағы
болғандағы
 шамасының қабылдайтын мүмкін мәндерінің арифметикалық ортасын атайды.
шамасының қабылдайтын мүмкін мәндерінің арифметикалық ортасын атайды.
Мысалы.
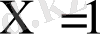 болғанда,
болғанда,
 мәндері
мәндері
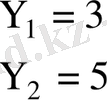
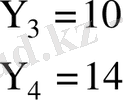
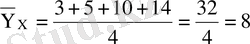
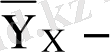 шартты орташа.
шартты орташа.
Анықтама 3
Егер бір кездейсоқ шама өзгергенде екінші кездейсоқ шаманың орта мәні өзгерсе, онда мұндай статистикалық тәуелділікті корреляциялық тәуелділік деп айтады. Сонымен
 және
және
 кездейсоқ шамаларының арасындағы корреляциялық байланыс мына формуламен беріледі
кездейсоқ шамаларының арасындағы корреляциялық байланыс мына формуламен беріледі
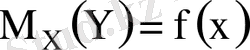 (7. 1)
(7. 1)
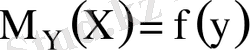 (7. 2)
(7. 2)
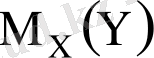 ,
,
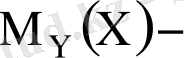 шартты математикалық үміттер. (7. 1), (7. 2) - моделдік регрессия теңдеулері деп аталады. Оларды табу үшін
шартты математикалық үміттер. (7. 1), (7. 2) - моделдік регрессия теңдеулері деп аталады. Оларды табу үшін
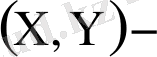 екі өлшемді кездейсоқ шаманың үлестіру заңын білу керек.
екі өлшемді кездейсоқ шаманың үлестіру заңын білу керек.
Жалпы регрессиялық моделдер. Регрессиялық модель жалпы түрде былай жазылады:
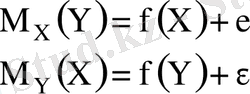
 - кездейсоқ фактор.
- кездейсоқ фактор.
Моделде
 кездейсоқ фактор болу себептері:
кездейсоқ фактор болу себептері:
1) Моделге барлық түсіндіруші айнымалылардың кірмеуі.
Кез келген регрессиялық модель нақты жағдайдың жеңілдетілген түрі болып табылады.
Мысалы,
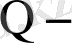 тауарға сұраныс,
тауарға сұраныс,
 тауардың бағасы,
тауардың бағасы,
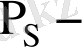 осы тауарды алмастырушы тауардың бағасы,
осы тауарды алмастырушы тауардың бағасы,
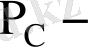 осы тауарды толықтырушы тауардың бағасы,
осы тауарды толықтырушы тауардың бағасы,
 тұтынушының кірісі,
тұтынушының кірісі,
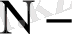 тұтынушылар саны,
тұтынушылар саны,
 тұтынушылар талғамы, тағы сол сияқты факторлар.
тұтынушылар талғамы, тағы сол сияқты факторлар.
Бұл мысалда салт дәстұр, ұлттық және діни ерекшеліктері, географикалық орыны, ауа райы және көптеген факторлар есептелмейді, яғни
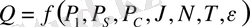
2) Моделдің функционалдық түрін дұрыс таңдай алмау, зерттелініп отырған процесті дұрыс білмеу немесе оның жиі өзгеруіне байланысты моделдеу функциясын дұрыс таңдай алмау.
3) Айнымалылардың күрделілігі. Көптеген моделдерде әрбір айнымалы күрделі бірнеше жай айнымалыларға тәуелді.
4) Өлшеу қателері. Модель қаншалықты сапалы болса да эмпирикалық мәліметтерге сәйкес келмейтін өлшеу қателері кездеседі.
5) Статистикалық мәліметтердің шектеулігі. Көбіне модель үздіксіз функция арқылы құрылады, ол үшін дискретті құрылымдағы мәліметтер қолданылады. Осындай айқыштық
 ауытқуына әсер етеді.
ауытқуына әсер етеді.
6) Адам факторын алдын-ала білмеу. Модель сапалы құрылса да, адам баласының ерекшеліктерін болжау мүмкін емес.
Зерттеу мақсатына және эмпирикалық мәліметтерге сәйкес сапалы регрессиялық модель құру күрделі және көп сатылы процесс. Оны үш сатыға бөлуге болады:
1) регрессия теңдеуінің түрін таңдау;
2) регрессия теңдеуінің параметрлерін анықтау;
3) регрессия теңдеудің сапалылығын талдау және моделдің эмпирикалық теңдеулеріне адекват екенін тексеру. h4>
Қос сызықтық регрессия және регрессия теңдеуінің сапасын тексеру (Гаусс-Марков теоремасы және детерминация коэффициенті) .
Сызықтық регрессия моделі экономикалық айнымалылар арасындағы тәуелділікті көрсетеді және жиі қолданатын моделге жатады. Сызықтық регрессия тәуелді айнымалы
 - тің математикалық үміті және бір түсіндіруші айнымалы
- тің математикалық үміті және бір түсіндіруші айнымалы
 (
(
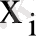 - тәуелсіз айнымалының
- тәуелсіз айнымалының
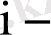 ші бақылаудағы мәні
ші бақылаудағы мәні
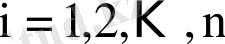 ) арасындағы сызықтық функция.
) арасындағы сызықтық функция.
(7. 3)
Әрбір
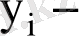 дің оның математикалық үмітінен ауытқуын еске алып, (3) теңдеуін былай жазамыз
дің оның математикалық үмітінен ауытқуын еске алып, (3) теңдеуін былай жазамыз
(7. 4)
(7. 4) - теориялық сызықтық регрессия моделі деп аталады;
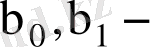 регрессияның теориялық параметрлері (теориялық коэффициенттері) ;
регрессияның теориялық параметрлері (теориялық коэффициенттері) ;
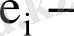 кездейсоқ ауытқулар.
кездейсоқ ауытқулар.
Жалпы түрде сызықтық регрессиялық модель былай жазылады
(7. 5)
Сызықтық регрессиялық талдау есебі:
 және
және
 айнымалылары үшін белгілі
айнымалылары үшін белгілі
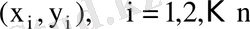 статистикалық мәліметтер бойынша
статистикалық мәліметтер бойынша
а)
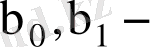 коэффициенттерінің ең жақсы бағаларын табу;
коэффициенттерінің ең жақсы бағаларын табу;
ә) моделдің параметрлері туралы статистикалық болжамдарды тексеру;
б) статистикалық мәліметтермен модель қаншалықты үйлесімді, яғни берілген мәліметтерге модель адекват бола ма?
Көлемі шектелген таңдама бойынша сызықтық регрессияның эмпирикалық теңдеуін жазайық
(7. 6)
мұнда
шартты математикалық үміт
бағасы,
эмпирикалық коэффициенттер, белгісіз параметрлер
дің бағалары.
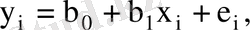
(7. 7)
 - ауытқуы теориялық кездейсоқ ауытқу
- ауытқуы теориялық кездейсоқ ауытқу
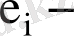 дің бағасы. Бас жиынтық пен таңдаманың көлемдері әртүрлі болғандықтан ылғи да
дің бағасы. Бас жиынтық пен таңдаманың көлемдері әртүрлі болғандықтан ылғи да
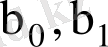 -эмпирикалық коэффициенттердің
-эмпирикалық коэффициенттердің
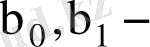 теориялық коэффициенттерден айырмашылығы болады. Берілген таңдама мәліметтерін пайдаланып
теориялық коэффициенттерден айырмашылығы болады. Берілген таңдама мәліметтерін пайдаланып
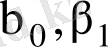 коффициенттерінің
коффициенттерінің
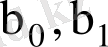 бағаларын тауып, бақылау бойынша алынған нүктелер
бағаларын тауып, бақылау бойынша алынған нүктелер
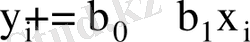
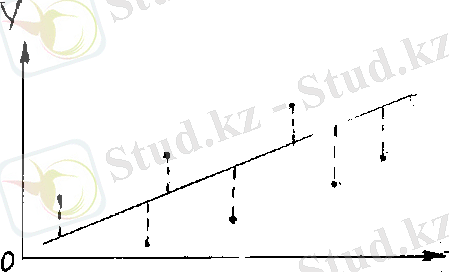
түзуіне жақын орналасатындай түзудің теңдеуін анықтау керек. Бір бас жиынтықтан алынған әртүрлі таңдамалар бойынша бір - бірінен айырмашылығы бар әртүрлі бағалар табылады.
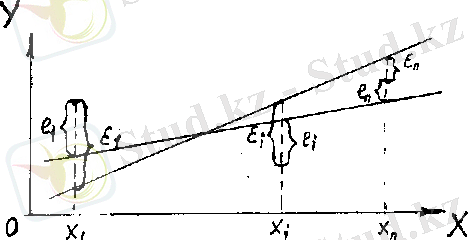
(7. 1-сурет)
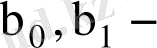 коэффициенттерін табудың ең көп таралған және теориялық негізделген әдісі ең кіші квадраттар әдісі болып табылады. Бұл әдіс келесі қосындының минимум мәнін табуға негізделген және есептеуге ыңғайлы қарапайым әдіс.
коэффициенттерін табудың ең көп таралған және теориялық негізделген әдісі ең кіші квадраттар әдісі болып табылады. Бұл әдіс келесі қосындының минимум мәнін табуға негізделген және есептеуге ыңғайлы қарапайым әдіс.
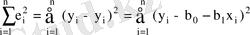
Ең кіші квадраттар әдісі
Берілген
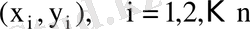 таңдама бойынша регрессияның эмпирикалық теңдеуінің коэффициенттері
таңдама бойынша регрессияның эмпирикалық теңдеуінің коэффициенттері
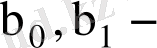 ді анықтайық. Бұл жағдайда келесі функцияның минимум мәнін іздейміз.
ді анықтайық. Бұл жағдайда келесі функцияның минимум мәнін іздейміз.
(7. 2-сурет)
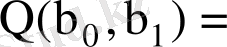
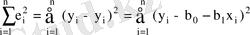
(7. 8)
 функциясы
функциясы
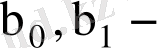 параметрлерінің квадраттық функциясы, себебі (
параметрлерінің квадраттық функциясы, себебі (
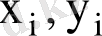 )
)
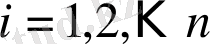 бақылау бойынша белгілі сандар. Екі айнымалының функциясының экстремум мәні болуының қажетті шартын пайдаланып, функцияның
бақылау бойынша белгілі сандар. Екі айнымалының функциясының экстремум мәні болуының қажетті шартын пайдаланып, функцияның
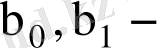 белгісіз параметрлері бойынша алынған дербес туындыларын нөлге теңестірейік.
белгісіз параметрлері бойынша алынған дербес туындыларын нөлге теңестірейік.
(7. 9)
(7. 10)
(7. 10) жүйесінің теңдеулерін
санына бөліп,
(7. 11)
мұнда
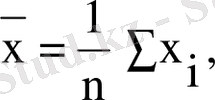
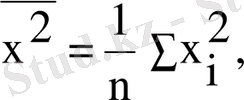
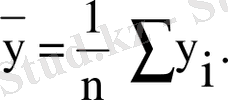
олай болса, ең кіші квадраттар әдісі бойынша белгісіз параметрлер бағасы
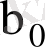 және
және
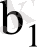 (11) формулаларымен анықталады.
(11) формулаларымен анықталады.
(7. 12)
немесе
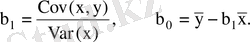
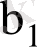 коэффициентін түрлендіріп
коэффициентін түрлендіріп
(7. 13)
мұнда
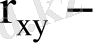 таңдаманың корреляция коэффициенті;
таңдаманың корреляция коэффициенті;
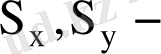 стандарттық ауытқулар,
стандарттық ауытқулар,
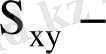 таңдаманың ковариациясы. Олай болса, регрессия коэффициенті ковариация және корреляция коэффициенттеріне пропорционал. Ендеше корреляция коэффициенті белгілі болса, (13) формуланы пайдаланып қос сызықтық регрессия коэффициентін табуға болады. Егер
таңдаманың ковариациясы. Олай болса, регрессия коэффициенті ковариация және корреляция коэффициенттеріне пропорционал. Ендеше корреляция коэффициенті белгілі болса, (13) формуланы пайдаланып қос сызықтық регрессия коэффициентін табуға болады. Егер
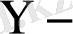 тің
тің
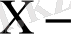 ке регрессиялық теңдеуінен
ке регрессиялық теңдеуінен
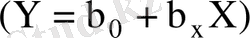 , осы эмпирикалық мәліметтер үшін
, осы эмпирикалық мәліметтер үшін
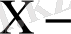 тің
тің
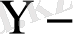 ке регрессиялық теңдеуі (
ке регрессиялық теңдеуі (
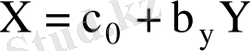 ) белгілі болса, онда
) белгілі болса, онда
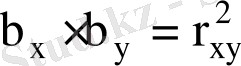
(7. 14)
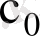 және
және
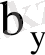 коэффициенттері келесі формуламен анықталады
коэффициенттері келесі формуламен анықталады
(7. 15)
Регрессия теңдеуінің сапасын тексеру. Ең кіші квадраттар әдісінің алғы шарттары (Гаусс-Марков шарттары) </h4>
1) барлық бақылаулар үшін кездейсоқ ауытқу
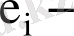 дің математикалық үміті нөлге тең
дің математикалық үміті нөлге тең
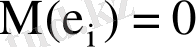 ;
;
2) кез келген
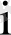 және
және
 бақылаулары үшін кездейсоқ ауытқулар дисперсиясы тұрақты
бақылаулары үшін кездейсоқ ауытқулар дисперсиясы тұрақты
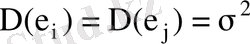 ;
;
3) кездейсоқ ауытқулар
және
,
үшін бір-біріне тәуелсіз;
4) кездейсоқ ауытқулар түсіндіруші айнымалылардан тәуелсіз
;
5) модель параметрлер арқылы сызықтық тәуелсіз.
Гаусс-Марков теоремасы
Егер (1-5) алғы шарттар орындалса, онда ең кіші квадраттар әдісі бойынша табылған бағалар келесі қасиеттерге ие болады:
- бағалар жылжымаған болады, яғни
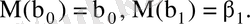
Бұл
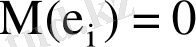 шартынан шығады және регрессия түзуін анықтауда ұдайы қате жоқ екенін көрсетеді;
шартынан шығады және регрессия түзуін анықтауда ұдайы қате жоқ екенін көрсетеді;
- бағалар орнықты, себебі бақылаулар саны өскенде бағалардың дисперсиясы нөлге ұмтылады
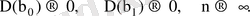
Басқаша айтқанда таңдаманың көлемі өсуіне байланысты бағалау дәлдігі өседі.
- баға тиімді, яғни параметрлердің басқа бағаларына қарағанда дисперсиясы ең кіші баға болып табылады.
Егер 2 және 3 алғышарттар орындалмаса, яғни ауытқулар дисперсиясы тұрақты емес және
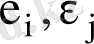 бір -бірімен байланысты болса, онда бағалар жылжымаған және орнықты болу қасиеттері сақталады, бірақ баға тиімді болмайды. Классикалық сызықтық регрессиялық модель құруда көрсетілген алғы шарттардан басқа бірнеше ұйғарым жасалады. Мысалы
бір -бірімен байланысты болса, онда бағалар жылжымаған және орнықты болу қасиеттері сақталады, бірақ баға тиімді болмайды. Классикалық сызықтық регрессиялық модель құруда көрсетілген алғы шарттардан басқа бірнеше ұйғарым жасалады. Мысалы
- түсіндіруші айнымалылар кездейсоқ шама болмайды;
- кездейсоқ ауытқулар қалыпты үлестірілген;
- бақылаулар саны түсіндіруші айнымалылар санына қарағанда едәуір үлкен;
- спецификациялау қатесі жоқ;
- жетілген мультиколлинеарлық жоқ.
Сызықтық регрессия теңдеуінің коэффициенттерінің интервалдық бағасы.
Ең кіші квадраттар әдісінің негізгі алғы шарттары математикалық үміті нөлге тең, дисперсиясы тұрақты
 ауытқуларының қалыпты үлестіруі туралы болжам болып табылады, яғни
ауытқуларының қалыпты үлестіруі туралы болжам болып табылады, яғни
 ~
~
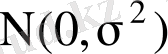 . Бұл болжамның нақтылығы ықтималдықтар теориясындағы белгілі орта шектік теоремаға негізделген. Егер кездейсоқ шама көптеген (бірнеше) тәуелсіз кездейсоқ шаманың қосындысына тең және әрбір қосылғыштың қосындыға әсері шамалы болса, онда қарастырып отырған кездейсоқ шама қалыпты үлестіруге жатады. Бірақ
. Бұл болжамның нақтылығы ықтималдықтар теориясындағы белгілі орта шектік теоремаға негізделген. Егер кездейсоқ шама көптеген (бірнеше) тәуелсіз кездейсоқ шаманың қосындысына тең және әрбір қосылғыштың қосындыға әсері шамалы болса, онда қарастырып отырған кездейсоқ шама қалыпты үлестіруге жатады. Бірақ
 кездейсоқ ауытқулары моделге кіргізілмеген тәуелсіз айнымалылардың шамаларына әсерін көрсетеді. Әдетте осындай айнымалылар саны өте көп, бірақ олардың жеке әсері өте аз. Сондықтан кездейсоқ ауытқуларды қарастыруда орта шектік теореманың шарттары толық орындалады деп айтуға болады.
кездейсоқ ауытқулары моделге кіргізілмеген тәуелсіз айнымалылардың шамаларына әсерін көрсетеді. Әдетте осындай айнымалылар саны өте көп, бірақ олардың жеке әсері өте аз. Сондықтан кездейсоқ ауытқуларды қарастыруда орта шектік теореманың шарттары толық орындалады деп айтуға болады.
 кездейсоқ шамалары қалыпты үлестірілген деп тұжырым жасауға болады, яғни
кездейсоқ шамалары қалыпты үлестірілген деп тұжырым жасауға болады, яғни
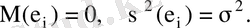 Онда ол тұжырым тек қана
Онда ол тұжырым тек қана
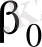 және
және
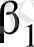 сызықтық регрессия теңдеуінің
сызықтық регрессия теңдеуінің
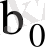 және
және
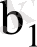 коэффициенттерінің сызықтық жылжымаған нүктелік бағалары ғана емес, сонымен қатар дәлдік кепілдігін беретін олардың интервалдық бағаларын табуға мүмкіндік береді. Жоғарыда көрсетілген болжамдар,
коэффициенттерінің сызықтық жылжымаған нүктелік бағалары ғана емес, сонымен қатар дәлдік кепілдігін беретін олардың интервалдық бағаларын табуға мүмкіндік береді. Жоғарыда көрсетілген болжамдар,
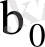 және
және
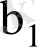 кездейсоқ шамалары қалыпты үлестірілген деп айтуға мүмкіндік береді. Шынында да, бізге белгілі болғандай, қалыпты үлестірілген кездейсоқ шамалардың сызықтық комбинациясы қалыпты үлестірілген кездейсоқ шама деп айтуға болады.
кездейсоқ шамалары қалыпты үлестірілген деп айтуға мүмкіндік береді. Шынында да, бізге белгілі болғандай, қалыпты үлестірілген кездейсоқ шамалардың сызықтық комбинациясы қалыпты үлестірілген кездейсоқ шама деп айтуға болады.
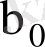 және
және
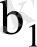 мына түрде жазылуы мүмкін:
мына түрде жазылуы мүмкін:
мұндағы
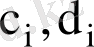 - тұрақты сандар. Басқаша айтқанда,
- тұрақты сандар. Басқаша айтқанда,
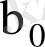 және
және
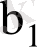 ,
,
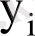 арқылы
арқылы
 -дің сызықтық функциялары болып табылады. Осыған сәйкес,
-дің сызықтық функциялары болып табылады. Осыған сәйкес,
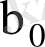 және
және
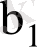 -де қалыпты үлестірілген. Алдында айтылғандай
-де қалыпты үлестірілген. Алдында айтылғандай
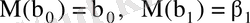 .
.
(7. 16)
мұнда
. Ендеше,
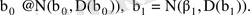
Жоғарыда көрсетілгендей статистика
(7. 17)
еркіндік дәрежесі
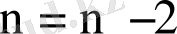 , Стьюдент үлестіруі болады. Әрі қарай
, Стьюдент үлестіруі болады. Әрі қарай
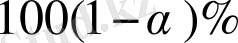 - тік сенімділік интервалын табу үшін Стьюдент үлестіруінің кризистік нүктелер кестесінен сенімділік ықтималдығы
- тік сенімділік интервалын табу үшін Стьюдент үлестіруінің кризистік нүктелер кестесінен сенімділік ықтималдығы
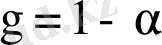 және еркіндік дәрежесі
және еркіндік дәрежесі
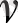 болатын,
болатын,
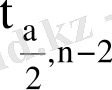 мәні табылады.
мәні табылады.
(7. 18)
(7. 19)
(7. 20)
Жақшадағы өрнекті түрлендіріп
(7. 21)
(7. 22)
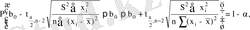 (7. 23)
(7. 23)
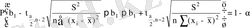 . (7. 24)
. (7. 24)
Қатынастар (
 ), сенімділікпен
), сенімділікпен
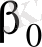 және
және
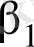 параметрлерін жабатын сенімділік интервалдары:
параметрлерін жабатын сенімділік интервалдары:
(7. 25)
. (7. 26)
Сенімділік интервалы регресияның
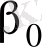 және
және
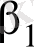 теориялық коэфициенттерінің табылған
теориялық коэфициенттерінің табылған
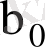 және
және
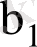 бағаларының
бағаларының
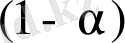 сенімділігіне сәйкес болатын интервалды анықтайды.
сенімділігіне сәйкес болатын интервалды анықтайды.
... жалғасы<h4>\ Детерминация коэффициенті
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz
