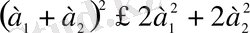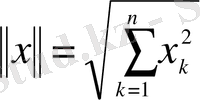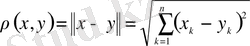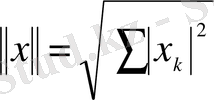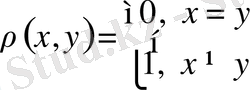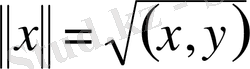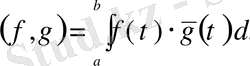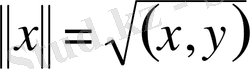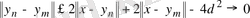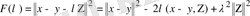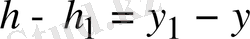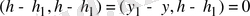Гильберт кеңістігінде Штурм-Лиувилл есебі үшін Рисс теоремасының қолданылуы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 49 бет
Таңдаулыға:
Рисс теоремасын Штурм-Ливилль есебі үшін пайдалану
Алдеков С.
М-29-1 у(в)
Жетекшісі ф. м. ғ. к., доцент Шырақбаев А. Б.
МАЗМҰНЫ
КІРІСПЕ . . . 5
1. НЕГІЗГІ АНЫҚТАМАЛАР . . . 6
1. 1. Сызықты кеңістіктің негізгі анықтамасы . . . 6
1. 2. Нормаланған кеңістік . . . 8
1. 3. Метрикалық кеңістік . . . 12
1. 4. Гильберт кеңістігі . . . 17
1. 5.
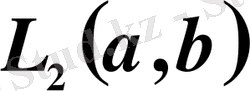 кеңістігі . . . 21
кеңістігі . . . 21
1. 6.
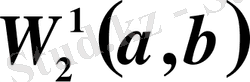 кеңістігі . . . 23
кеңістігі . . . 23
2. Штурм Лиувилл есебін зерттеуде Рисс теоремасының кейбір қолданылулары . . . 26
2. 1. Сызықты операторлар теориясының элементтері . . . 26
2. 2. Рисс теорамасы . . . 30
2. 3. Штурм-Лиувилл операторы . . . 37
2. 4. Рисс теоремасын Штурм-Ливилль есебі үшін пайдалану . . . 40
ҚОРЫТЫНДЫ . . . 43
Пайдаланылған әдебиеттер тізімі . . . 44
КІРІСПЕ
Тақырыптың өзектілігі. Штурм - Лиувилл операторының теориясы осы күнге дейін қолданбылылық әдісін жойған жоқ. Себебі, Штурм -Лиувилль операторы математиканың модельдік операторларының бірі болып саналады, көп жағдайларды зерттеулердің жаңа әдістерін осы операторға пайдаланып тексеруден өткізеді.
Алғашқылардың бірі болып Эверитт және Гирц әсiресе Штурм-Лиувииль операторына тиянақты зерттеулер жүргiздi. Өйткенi, ол оператор олардың ұсынып отырған зерттеу әдiстері үшiн “тексерiс текпiшегi” iспеттес едi. Олардың зерттеу әдiсi, Штрум-Лиувиль операторының Грин функциясын шексiздiкте қалай өзiн көрсететiндiгiн зерттеуде пайдалынатын классикалық тәсiл-дердi пайдалануға негiзделiнген еді.
Жұмыстың мақсаты.
Дипломдық жұмыстың мақсаты
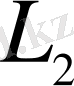 Гильберт кеңістігінде берілген Штурм-Лиувилл есебі үшін Рисс теоремасын зерттеу болып табылады.
Гильберт кеңістігінде берілген Штурм-Лиувилл есебі үшін Рисс теоремасын зерттеу болып табылады.
Зерттеу әдістемесі. Штурм-Лиувилл операторының шешімінің бар болуын дәлелдеу мәселесі көптеген ғалымдардың жұмыстарында қарастырылған: Ж. -Л. Лионс, А. Куфнер, С. Фучик және т. б. А. Куфнер, С. Фучик жұмыстарында шешімнің бар болуы Грин әдісімен, яғни сызықты түрге келтіру арқылы дәлелденеді. Ал Ж. -Л. Лионс өз зерттеулерінде Липшиц әдісін қолданады. Мұндағы негізгі орталық идея -дифференциалдық теңдеулер үшін шектік есептердің шешімдерінің бар болуын дәлелдеуде Рисс теоремасын пайдалану мәселесін шешу болып табылады.
Бұл мәселені шешуде шешім ұғымын кеңейту қажеттілігі туындады, яғни шектік есептердің классикалық қойылымдары жалпыланғандармен (обобщенными) алмастырылды, яғни профессор М. Б. Мұратбековтың енгізген әдісі қолданылды.
Ғылыми жаңашылдығы.
Дипломдық жұмыста Штурм - Лиувилл операторы үшін Рисс теоремасының қолданылуы зерттелген.
Теориялық және практикалық құндылығы. Шешімнің бар болуын дәлелдеу арқылы біз оның жалғыз болуы, қандай процесте орын алатыны мен әр түрлі жағдайларда шешімнің қандай болатынын зерттей аламыз. Бұл жұмыста, шектік есептердің классикалық қойылымдары жалпыланған шешімдермен алмастырылды
Дипломдық жұмыс нәтижесі. Зерттеу объектісі ретінде келесі Штурм - Лиувилл операторын зерттеу қарастырылады
Ly=-y'' + q(x) y (*)
мұндағы
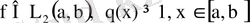
 (**)
(**)
Диплом жұмысының құрылымы. Дипломдық жұмыс кіріспе мен екі бөлімнен, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспе де тақырыптың өзектілігі негізделген, негізгі мақсаттары келтірілген, жұмыстың жаңалығы мен теориялық және практикалық маңыздылығы анықталған.
Бірінші бөлімде қажетті ұғымдар қарастырылан. Бұл бөлім көмекші ретінде көрсетілген. Мұнда сызықты, нормаланған, Гильберт,
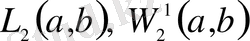 кеңістіктері ұғымдарының анықтамалары қарастырылған.
кеңістіктері ұғымдарының анықтамалары қарастырылған.
Екінші бөлім Штурм Ливилл операторы туралы және оның шешімін табуда Рисс теоремасының қолданылуын дәлелдеуге арналған.
1. НЕГІЗГІ АНЫҚТАМАЛАР
- 1. 1. Сызықты кеңістіктің негізгі анықтамасы
Егер Е жиынының x, y элементтері үшін келесі қасиеттер орындалса, онда оны сызықты кеңістік деп атайды:
А) егер Е кеңістігінде қосынды операциясы орындалса
1. егер
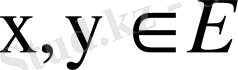 үшін
үшін
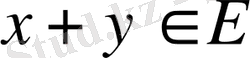 орындалса
орындалса
2.
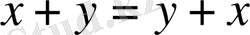 орындалса
орындалса
3.
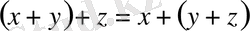 орындалса
орындалса
4.
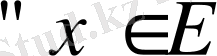 үшін
үшін
 орындалатындай нолдік элемент табылса
орындалатындай нолдік элемент табылса
Б) Е- де
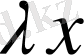 көбейтіндісі анықталып, келесі қаситеттер орындалса,
көбейтіндісі анықталып, келесі қаситеттер орындалса,
5. егер
 болса, онда
болса, онда
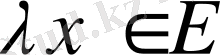 ;
;
6.
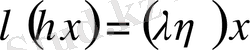 ;
;
7.
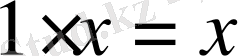
8.
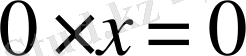
9.
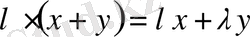 ;
;
10.
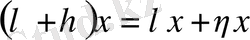 ;
;
Және бұл жағдайда кері элемент
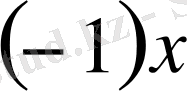 немесе -х табылады.
немесе -х табылады.
7, 8, 10 бойынша
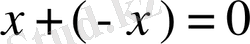 .
.
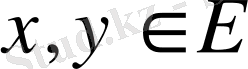 элементтері оның векторлары деп аталады.
элементтері оның векторлары деп аталады.
 . . . сандық көбейткіштер ретінде сызықты кеңістікте нақты немесе комплекс сандары алынады. Бірінші жағдайда Е нақты сызқыт кеңістік деп, ал екінші жағдайда комплекс сызықты кеңістік деп аталады.
. . . сандық көбейткіштер ретінде сызықты кеңістікте нақты немесе комплекс сандары алынады. Бірінші жағдайда Е нақты сызқыт кеңістік деп, ал екінші жағдайда комплекс сызықты кеңістік деп аталады.
Сызықты кеңістікте векторалардың сызықты және сызықты емес тәуелділік ұғымы енгізіледі. Е кеңістігінің
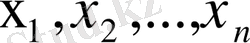 векторлары үшін
векторлары үшін
(1. 1. 1)
теңдігінен
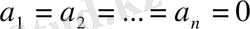 теңдігі орындалса, бұл вектолар сызықты тәуелсіз деп аталынады. Кері жағдайда (яғни (1. 1. 1) теңдігінде ең болмағанда бір
теңдігі орындалса, бұл вектолар сызықты тәуелсіз деп аталынады. Кері жағдайда (яғни (1. 1. 1) теңдігінде ең болмағанда бір
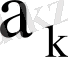 коэффициенті нолден өзгеше болса)
коэффициенті нолден өзгеше болса)
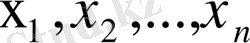 векторлары сызықты тәуелді деп аталады.
векторлары сызықты тәуелді деп аталады.
Егер Е кеңістігінде
 сызықты тәуелсіз векторлар бар болса, ал барлық
сызықты тәуелсіз векторлар бар болса, ал барлық
 векторы сызықты тәуелді болса, онда Е кеңістігінің өлшемі
векторы сызықты тәуелді болса, онда Е кеңістігінің өлшемі
 - ге тең деп айтады. Егер әрбір
- ге тең деп айтады. Егер әрбір
 үшін Е кеңістігінде
үшін Е кеңістігінде
 сызықты тәуелсіз векторлары бар болса, онда Е кеңістігінің өлшемділігі шексіздікке тең деп айтады.
сызықты тәуелсіз векторлары бар болса, онда Е кеңістігінің өлшемділігі шексіздікке тең деп айтады.
Е кеңістігінде
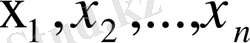 векторлары берілсін. Онда барлық
векторлары берілсін. Онда барлық
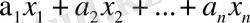 сызықты комбинациялар Е -нің сызықты ішкі кеңістігін құрайды. Оның өлшемділігі
сызықты комбинациялар Е -нің сызықты ішкі кеңістігін құрайды. Оның өлшемділігі
 - нен аспайды.
- нен аспайды.
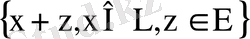 түріндегі жиын, мұндағы
түріндегі жиын, мұндағы
 - Е кеңістігінің ішкі кеңістігі, ал
- Е кеңістігінің ішкі кеңістігі, ал
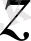 - Е кеңістігіндегі фиксирленген элемент сызықты көпбейнелік деп аталады.
- Е кеңістігіндегі фиксирленген элемент сызықты көпбейнелік деп аталады.
- мысал. сызығы, яғни, кәдімгі арифметикалық қосу және көбейту, көбейту амалдары орындалатын нақты сандар жиыны сызықты кеңістік болады.
- мысал. Кәдімгі функцияларды қосу және оларды сандарға көбейту амалдары орындалатын үздіксіз (нақты немесе комплексті) функциялар кеңістігі кез кеңістігін құрады. Бұл кеңістіктің функционалдық анализде алатын орны ерекше.
- Мысал. - сызықты кеңістік. Себебі оның элементтері ретінде
(1. 1. 2)
шартын қанағаттандыратын сандар (нақты немесе комплексті)
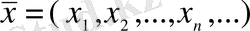
тізбегі алынады, ол сандар үшін
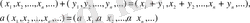
амалдары орындалған. (1. 1. 2) шартын қанағаттандыратын екі сандар тізбегі үшін осы шарттың орын алатындығы мына
элементар теңсіздіктен келіп шығады.
- 1. 2. Сызықты нормаланған кеңістік
Анықтама.
Егер әрбір
 үшін норма деп аталатын,
үшін норма деп аталатын,
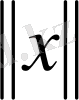 түрінде белгіленетін нақты сан сәйкестендірілсе және ол үшін келесі аксиомалар орындалса, онда Е -сызықты кеңістігі нормаланған деп аталады:
түрінде белгіленетін нақты сан сәйкестендірілсе және ол үшін келесі аксиомалар орындалса, онда Е -сызықты кеңістігі нормаланған деп аталады:
1.
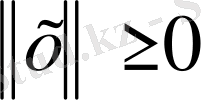 , және
, және
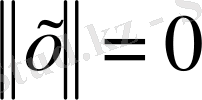 , егер
, егер
 ;
;
2.
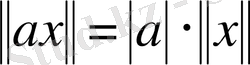 ;
;
3.
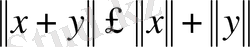 .
.
Норма үшін келесі теңсіздік дәлелденеді

Нормаланған кеңістікке мысалдар келтірейік.
1-мысал.
Егерде кез келген
 саны үшін
саны үшін
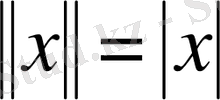 деп алатын болсақ, онда түзу сызығы нормаланған кеңістік болады.
деп алатын болсақ, онда түзу сызығы нормаланған кеңістік болады.
2-мысал.
Егер элементтері
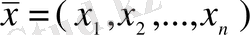 болатын нақты
болатын нақты
 өлшемді кеңістікте
өлшемді кеңістікте
деп алсақ, онда барлық аксиомалар орындалатын болады.
формуласы
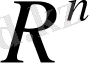 -дегі (осы кеңістіктегі) қарастырып отырған өлшемді (метриканы) анықтайды.
-дегі (осы кеңістіктегі) қарастырып отырған өлшемді (метриканы) анықтайды.
Осы сызықты кеңістікте
(1. 2. 1)
нормасын немесе
(1. 2. 2)
нормасын енгізуге болады. Осы жағдайлардың әрқайсысында нормалар аксиомаларының орындалатындығын тексеру қиын емес.
Комплексті
 -өлшемді кеңістікте
-өлшемді кеңістікте
нормасын немесе (1. 2. 1) мен (1. 2. 2) -нің кез келгенін енгізуге болады.
3-мысал.
Үздіксіз функциялар кеңістігінің
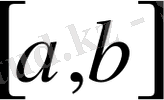 кесіндісінде
кесіндісінде
(
бойынша)
нормасын анықтайық.
Норма аксиомаларының орындалатындығын оңай тексеруге болады.
4-мысал .
сызықтық кеңістігіндегі
функциясының мәні
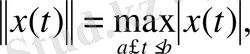 (1. 2. 3)
(1. 2. 3)
теңдігімен анықталады.
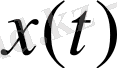 функциясы
функциясы
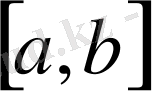 кесіндісінде үзіліссіз болғандықтан, оның модулі де үзіліссіз, демек, оның осы кесіндіде максимумы бар. Сондықтан (1. 2. 3) теңдігі
кесіндісінде үзіліссіз болғандықтан, оның модулі де үзіліссіз, демек, оның осы кесіндіде максимумы бар. Сондықтан (1. 2. 3) теңдігі
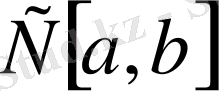 жиынының әрбір элементі
жиынының әрбір элементі
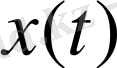 үшін оның нормасының мәнін бірмәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
үшін оның нормасының мәнін бірмәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
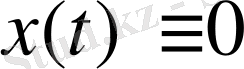 екендігі түсінікті. Сонымен бірінші аксиоманың орындалуы айқын. Енді
екендігі түсінікті. Сонымен бірінші аксиоманың орындалуы айқын. Енді
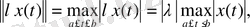 (1. 2. 4)
(1. 2. 4)
теңдігі мен
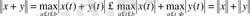 (1. 2. 5)
(1. 2. 5)
теңсіздігі норманың қалған екі аксиомасы да орындалатынын көрсетеді.
5-мысал.
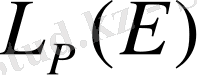 - Лебег кеңістігі.
Е жиынында қосындыланатын функциялардың жиыны сызықтық кеңістік құрайды. Бұл кеңістік
- Лебег кеңістігі.
Е жиынында қосындыланатын функциялардың жиыны сызықтық кеңістік құрайды. Бұл кеңістік
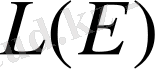 түрінде таңбаланады. Енді
түрінде таңбаланады. Енді
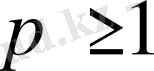 ке-келген нақты сан болсын. Е жиынында
ке-келген нақты сан болсын. Е жиынында
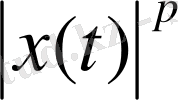 дәрежесі қосындыланатын
дәрежесі қосындыланатын
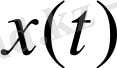 функцияларының жиыны да сызықтық кеңістік құрайтыны белгілі. Осы сызықтық кеңістік
функцияларының жиыны да сызықтық кеңістік құрайтыны белгілі. Осы сызықтық кеңістік
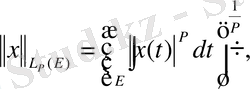 (1. 2. 6)
(1. 2. 6)
теңдігімен анықталған норма енгізу арқылы нормаланған сызықтық кеңістікке айналады. Бұл кеңістік әдетте
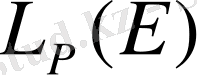 түрінде белгіленеді. Сонымен, әрбір
түрінде белгіленеді. Сонымен, әрбір
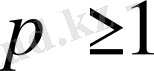 санына орай сызықтық кеңістік
санына орай сызықтық кеңістік
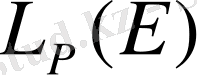 анықталады. Осы кеңістіктер Лебег кеңістіктері деп аталады. Егер
анықталады. Осы кеңістіктер Лебег кеңістіктері деп аталады. Егер
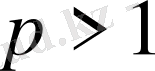
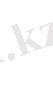 болса, Онда
болса, Онда
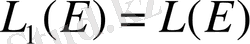 түрінде жазылып, қосындыланатын функциялар кеңістігін белгілейді.
түрінде жазылып, қосындыланатын функциялар кеңістігін белгілейді.
(1. 2. 6) теңдігі арқылы анықталған норманың тиісті аксиомаларды қанағаттандыратынына тоқталайық. Егер қайсыбір
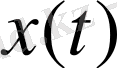 үшін
үшін
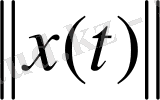 нормасының нөлге тең болуы, теңдіктің оң жағындағы интеграл нөлге тең деген сөз. Демек, Лебег интегралының қасиеті бойынша
нормасының нөлге тең болуы, теңдіктің оң жағындағы интеграл нөлге тең деген сөз. Демек, Лебег интегралының қасиеті бойынша
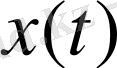 функциясы нөлге пара-пар функция. Осыған байланысты
Лебег кеңістіктерінде қабылданған маңызды келісім-бұл кеңістікке пара-пар функциялар ажыратылмайды, өзара пара-пар функциялардың бәрі кеңістіктің бір элементі болып есептеледі.
Демек, Е жиынында нөлге пра-пар, яғни осы жиынның барлық жерінде дерлік нөлге тең функция, кеңістіктің нөлдік элементі
функциясы нөлге пара-пар функция. Осыған байланысты
Лебег кеңістіктерінде қабылданған маңызды келісім-бұл кеңістікке пара-пар функциялар ажыратылмайды, өзара пара-пар функциялардың бәрі кеңістіктің бір элементі болып есептеледі.
Демек, Е жиынында нөлге пра-пар, яғни осы жиынның барлық жерінде дерлік нөлге тең функция, кеңістіктің нөлдік элементі
 ретінде қабылданады. Сондықтан (1. 2. 6) теңдігімен анықталған норма норманың бірінші аксиомасын қанағаттандырады. Онан соң, бұл норманыңекінші (біртектілік) аксиомаға сай екені түсінікті. Енді қалған мәселе - норма (1. 2. 6) үшбұрыш теңсіздігін, атап айтқанда,
ретінде қабылданады. Сондықтан (1. 2. 6) теңдігімен анықталған норма норманың бірінші аксиомасын қанағаттандырады. Онан соң, бұл норманыңекінші (біртектілік) аксиомаға сай екені түсінікті. Енді қалған мәселе - норма (1. 2. 6) үшбұрыш теңсіздігін, атап айтқанда,
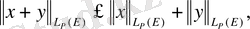 (1. 2. 7)
(1. 2. 7)
теңсіздігін қанағаттандыратынын дәлелдеу.
Алдымен Гельдер теңсіздігін еске алайық
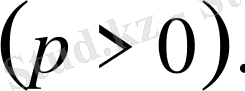
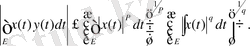 (1. 2. 8)
(1. 2. 8)
Мұнда
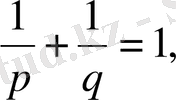 немесе осыдан
немесе осыдан
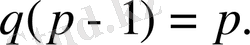 Енді (1. 2. 7) теңсіздігін дәлелдейік. Келесі түрлендіруде
Енді (1. 2. 7) теңсіздігін дәлелдейік. Келесі түрлендіруде
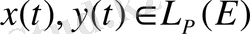 сондай-ақ
сондай-ақ
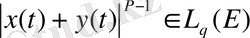 екендігі пайдаланылады. Ықшамдық үшін норманың қосындысы
екендігі пайдаланылады. Ықшамдық үшін норманың қосындысы
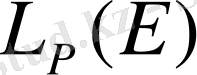 белгісін жазбаймыз.
белгісін жазбаймыз.
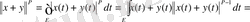
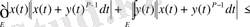
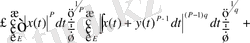
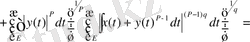
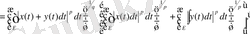
Мүнда бірінші теңдік анықтама бойынша. Екінші теңдіктен кейін қосындының бір дәрежесі жеке жазылды да, келесі теңсіздіктен кейін екі қосындыға жіктеліп, олардың әрқайсысына Гельдер теңсіздігі қолданылды. Алынған теңсіздік норманың анықтамасы бойынша мына түрде жазылады:
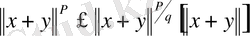
осы теңсіздіктің екі жағын
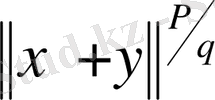 санына бөліп, (1. 2. 7) теңдігіне келеміз. Сонымен теңдік (1. 2. 6) норма анықтайтыны дәлелденді, демек,
санына бөліп, (1. 2. 7) теңдігіне келеміз. Сонымен теңдік (1. 2. 6) норма анықтайтыны дәлелденді, демек,
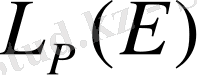 нормаланған сызықты кеңістік болады.
нормаланған сызықты кеңістік болады.
Ескерту. (1. 2. 7) теңдігін ашып жазайық:
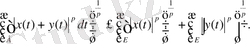 (1. 2. 9)
(1. 2. 9)
Мұның дәлелі
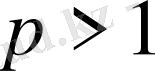 үшін келтірілді. Ал
үшін келтірілді. Ал
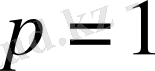 болса, онда бұл теңсіздік модуль мен интегралдың қарапайым қасиеттерінің салдары екені айқын. Сонымен (1. 2. 9) теңсіздігі
болса, онда бұл теңсіздік модуль мен интегралдың қарапайым қасиеттерінің салдары екені айқын. Сонымен (1. 2. 9) теңсіздігі
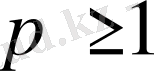 үшін орындалатыны айқындалады.
үшін орындалатыны айқындалады.
Бұл теңсіздік Минковский теңсіздігі деп аталады. Дәлірек айтқанда, бұл Минковский теңсіздігінің интегралдық түрі.
1. 3. Метрикалық кеңістік
Анықтама 1. 3. 1. Метрикалық кеңістік деп
жұбын айтамыз, мұнда Е - кейбір жиын және
- нақты функция, кез келген
үшін бұл функция төмендегі шарттарды (аксиомалады) қанағаттандырады:
1.
және
тек сонда ғана, егер
болса;
2. (симметрия аксиомасы)
;
3. (үшбұрыш аксиомасы)
;
ρ функциясы арақашықтық немесе Е-дегі метрика деп аталады.
Е-дегі норма
өлшемін туындайды.
1- мысал. Еркінше алынған элементтер жиыны үшін
деп ала отырып, біз оқшауланған нүктелер өлшемді кеңістігін аламыз.
2- мысал.
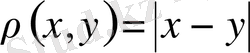 арақашықтығы анықталған нақты сандар жиыны
арақашықтығы анықталған нақты сандар жиыны
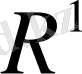 өлшемдік кеңістігін құрайды.
өлшемдік кеңістігін құрайды.
3-мысал.
1. 2. пунктіндегі 3- мысалдағыдай
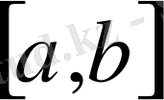 аралығында үздісіз болатын барлық функциялар жиынын қарастырайық, тек мұнда арақашықтықты былай анықтаймыз:
аралығында үздісіз болатын барлық функциялар жиынын қарастырайық, тек мұнда арақашықтықты былай анықтаймыз:
.
Мұндай метрикалық кеңістікті біз
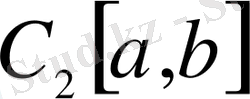 деп белгілейміз және оны квадраты өлшемді үзіліссіз функциялар кеңістігі деп атайтын боламыз. Бұл жерде 1) және 2) аксиомаларының орындалатыны айқын. Ал үшбұрыш аксиомасы тікелей Коши-Буняковский теңсіздігінің
деп белгілейміз және оны квадраты өлшемді үзіліссіз функциялар кеңістігі деп атайтын боламыз. Бұл жерде 1) және 2) аксиомаларының орындалатыны айқын. Ал үшбұрыш аксиомасы тікелей Коши-Буняковский теңсіздігінің
интегралдық формасынан келіп шығады. Осы теңсіздік, мысалы, дұрыстығы оңай тексерілетін төмендегі тепе-теңдіктен алынады:
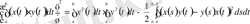 .
.
Норма Е- де
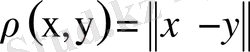 метриканы анықтайды.
метриканы анықтайды.
Нормаланған кеңістік метрикасы анықталған метрикалық кеңістік ретінде де қарастырылады.
Е нормаланған кеңістікте келесідей анықталған жиынды қарастырайық.
<
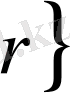
Мұндағы
 - фиксирленген нүкте, ал
- фиксирленген нүкте, ал
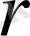 >0.
>0.
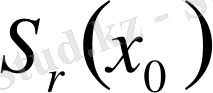 жиыны центрі
жиыны центрі
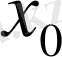 , радиусы
, радиусы
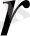 болатын ашық шар деп аталады.
болатын ашық шар деп аталады.
Дәл осы сияқты,
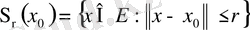
жиыны центрі
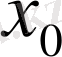 , радиусы
, радиусы
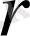 тұйық шар деп аталады.
тұйық шар деп аталады.
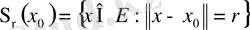 жиыны сфера деп аталады.
жиыны сфера деп аталады.
Нормаланған Е жиынында
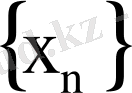 тізбегін қарастырайық.
тізбегін қарастырайық.
Анықтама 1. 3. 2.
Егер
 ұмтылғандағы
ұмтылғандағы
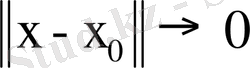 екендігі орындалса, онда
екендігі орындалса, онда
 элементі
элементі
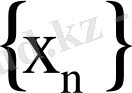 тізбегінің шегі деп аталады.
тізбегінің шегі деп аталады.
Егер
 элементі
элементі
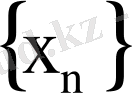 тізбегінің шегі болса, онда
тізбегінің шегі болса, онда
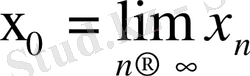 немесе
немесе
 -ғы
-ғы
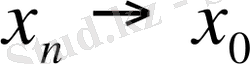 деп белгілейміз.
деп белгілейміз.
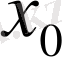 нүктесінің аймағы ретінде кез келген
нүктесінің аймағы ретінде кез келген
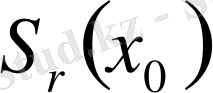 ашық шарын таңдап алайық.
ашық шарын таңдап алайық.
Анықтама 1. 3. 3.
Егер
 жиыны белгілі бір шардың ішінде жатса, оны шектелген жиын деп атайды. Дәлірек айтсақ,
жиыны белгілі бір шардың ішінде жатса, оны шектелген жиын деп атайды. Дәлірек айтсақ,
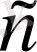 >0 саны табылып, барлық
>0 саны табылып, барлық
 үшін
үшін
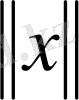 >0 теңсіздігі орындалса, онда М шектелген деп аталады.
>0 теңсіздігі орындалса, онда М шектелген деп аталады.
Әрбір жинақталатын тізбек шектелген.
Метрикалық кеңістіктегідей, егер
 үшін әрбір
үшін әрбір
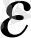 >0 саны табылып және оған
>0 саны табылып және оған
 саны сәйкестендіріліп,
саны сәйкестендіріліп,
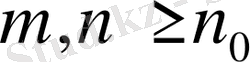 болғанда
болғанда
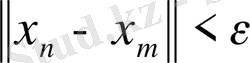 теңсіздігі орындалса
теңсіздігі орындалса
 тізбегі фундаментальды деп аталады.
тізбегі фундаментальды деп аталады.
Анықтама 1. 3. 3. Егер нормаланған кеңістіктегі әрбір фундаментальды кеңістік жинақталатын болса, ол толық деп аталады. Толық кеңістіктер банах кеңістіктері деп те аталады.
Анықтама 1. 3. 4.
Егер М жиынынан фундаментальды
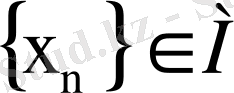 тізбегін бөліп алуға болатын болса, онда Е нормаланған кеңістіктің М жиыны компактылы деп аталады.
тізбегін бөліп алуға болатын болса, онда Е нормаланған кеңістіктің М жиыны компактылы деп аталады.
Метрикалық кеңістікті толықтыру
Егер кеңістік толық болмаса, оған оның шектік элементтерін қосып толықтыруға болады.
Анықтама 1. 3. 5.
Егер
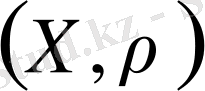 метрикалық кеңістіктегі
метрикалық кеңістіктегі
 жиынының
жиынының
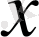 элементіне
элементіне
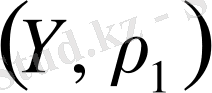 метрикалық кеңістігінің қайсыбір
метрикалық кеңістігінің қайсыбір
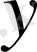 элементі сәйкес қойылған болса, онда
элементі сәйкес қойылған болса, онда
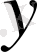 элементі
элементі
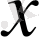 элеметінің бейнесі деп аталады.
элеметінің бейнесі деп аталады.
 жиынының элементтерінің бейнелерінің жиыны
жиынының элементтерінің бейнелерінің жиыны
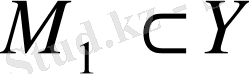 болсын. Онда біз
болсын. Онда біз
 жиынында оны
жиынында оны
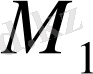 жиынына түрлендіретін
бейнелеу
жиынына түрлендіретін
бейнелеу
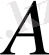 анықталған дейміз.
анықталған дейміз.
Әрбір жеке жағдайларда бейнелеу функция, оператор, т. б. дербес аттармен аталады және
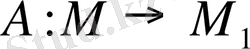 немесе
немесе
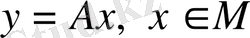 т. б. түрлерде жазылады. Осындайда біз: «А бейнелеуі
т. б. түрлерде жазылады. Осындайда біз: «А бейнелеуі
 жиынын
жиынын
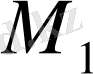 жиынына бейнелейді (аударады, түрлендіреді, көшіреді) » - дейміз.
жиынына бейнелейді (аударады, түрлендіреді, көшіреді) » - дейміз.
Анықтама 1. 3. 6.
Егер
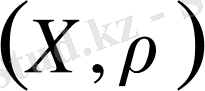 метрикалық кеңістігі
метрикалық кеңістігі
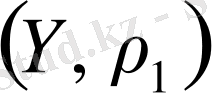 метрикалық кеңістігіне
метрикалық кеңістігіне
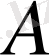 бейнелеуімен өзара бірмәнді түрленетін болса және кез-келген
бейнелеуімен өзара бірмәнді түрленетін болса және кез-келген
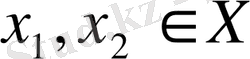 үшін және бұлардың бейнелеулері
үшін және бұлардың бейнелеулері
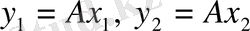 үшін
үшін
 теңдігі орындалатын болса, онда
теңдігі орындалатын болса, онда
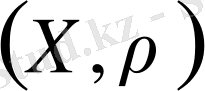 және
және
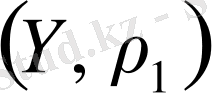 кеңістіктері
изометриялы кеңістіктер
деп аталады. Ал мұндай бейнелеу
изометрия
деп аталады.
кеңістіктері
изометриялы кеңістіктер
деп аталады. Ал мұндай бейнелеу
изометрия
деп аталады.
Анықтама 1. 3. 7. Егер:
1) Х жиынында
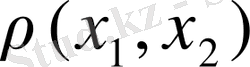 метрикасы анықталған, У жиынында
метрикасы анықталған, У жиынында
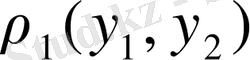 метрикасы анықталған болса;
метрикасы анықталған болса;
2) Х және
 жиындары изометриялы жиындар, яғни кез-келген
жиындары изометриялы жиындар, яғни кез-келген
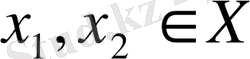 және олардың бейнелері
және олардың бейнелері
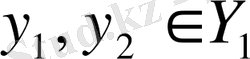 үшін
үшін
 болса;
болса;
3)
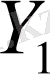 жиыны
жиыны
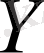 жиынында тығыз орналасқан болса, онда
жиынында тығыз орналасқан болса, онда
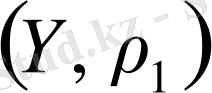 кеңістігі
кеңістігі
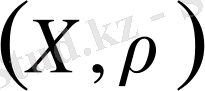 кеңістігінің толықтыруы деп аталады.
кеңістігінің толықтыруы деп аталады.
Енді толықтыру теоремасын тұжырымдайық.
Теорема 1. 3. 1.
Әрбір толық емес кеңістікті толықтыруға болады, яғни,
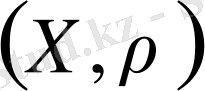 метрикалық кеңістігі толық емес болса, онда оның толықтыруы болатын
метрикалық кеңістігі толық емес болса, онда оның толықтыруы болатын
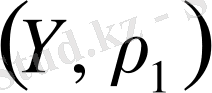 толық метрикалық кеңістігі әрқашан болады.
толық метрикалық кеңістігі әрқашан болады.
Мысал.
Рационал сандардың жиынында
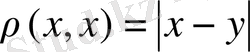 теңдігімен анықталған метрика енгізу нәтижесінде түзілген метрикалық кеңістік
теңдігімен анықталған метрика енгізу нәтижесінде түзілген метрикалық кеңістік
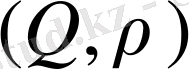 толық кеңістік емес. Оған көз жеткізу үшін, мысалы,
толық кеңістік емес. Оған көз жеткізу үшін, мысалы,
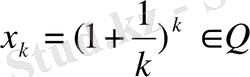 тізбегін қарастырайық. Бұл жинақты (демек, фундаменталь) тізбек екені математикалық анализ курсынан белгілі. Басқаша айтқанда тізбектің шегі
тізбегін қарастырайық. Бұл жинақты (демек, фундаменталь) тізбек екені математикалық анализ курсынан белгілі. Басқаша айтқанда тізбектің шегі
 жиынында жоқ.
жиынында жоқ.
Анықтама 1. 3. 8.
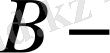 Банах кеңістігі, ал
Банах кеңістігі, ал
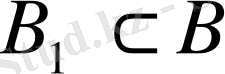 оның ішкі жиыны болсын. Егер
оның ішкі жиыны болсын. Егер
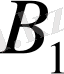 жиынының өзі сызықтық кеңістік құрайтын болса және ол
жиынының өзі сызықтық кеңістік құрайтын болса және ол
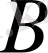 кеңістігінің нормасы бойынша толық кеңістік болса, онда
кеңістігінің нормасы бойынша толық кеңістік болса, онда
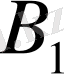 кеңістігі
кеңістігі
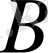 кеңістігінің
ішкі кеңістігі
деп аталады.
кеңістігінің
ішкі кеңістігі
деп аталады.
Мысал.
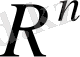 кеңістігінде
кеңістігінде
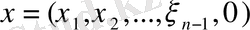 түріндегі векторлардың жиынын А әрпімен белгілейік Осы түрдегі екі вектордың қосындысы да, санға көбейтіндісі де осы түрдегі вектор болатыны, яғни А жиынында жататыны айқын. Демек, А жиыны сызықтық кеңістік құрайды. Енді
түріндегі векторлардың жиынын А әрпімен белгілейік Осы түрдегі екі вектордың қосындысы да, санға көбейтіндісі де осы түрдегі вектор болатыны, яғни А жиынында жататыны айқын. Демек, А жиыны сызықтық кеңістік құрайды. Енді
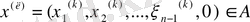 тізбегі
тізбегі
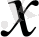 векторына жинақталатын болса, онда
векторына жинақталатын болса, онда
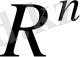 кеңістігіндегі жинақтылық - координаттар бойынша жинақтылық болғантықтан,
кеңістігіндегі жинақтылық - координаттар бойынша жинақтылық болғантықтан,
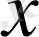 векторының координаттары
векторының координаттары
 демек оның соңғы координаты
демек оның соңғы координаты
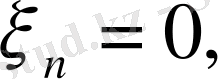 яғни
яғни
 .
.
 жиыны ішкі кеңістік екені дәлелденді.
жиыны ішкі кеңістік екені дәлелденді.
Метрикалық кеңістіктерге мысалдар
1)
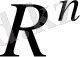 кеңістігінде кез келген әртүрлі реттелген
кеңістігінде кез келген әртүрлі реттелген
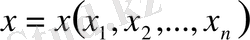 және
және
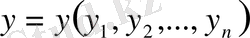 нүктелері үшін метриканы мына түрде аламыз.
нүктелері үшін метриканы мына түрде аламыз.
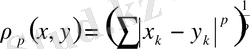 .
.
мұндағы:
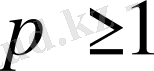 .
.
1) және 2) аксиомалардың орындалатыны жеңіл көрініп тұр.
3) аксиоманың орындалатынын тексерейік
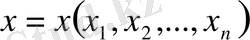 ,
,
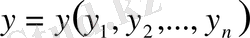 және
және
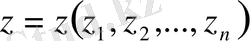 болсын.
болсын.
Дәлірек айтқанда біз мынадай теңсіздікті дәлелдеуіміз керек
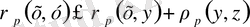
Егер
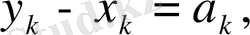
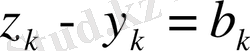
деп белгілесек, онда
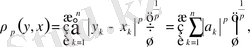
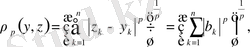
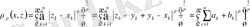
Енді (2) теңсіздік пен соңғы келтірілген теңсіздіктерді пайдаланып жазсақ мынадай түрге енеді.
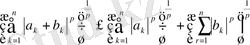 -
-
бұл Миньковский теңсіздігі ,
олай болса (2) теңсіздігі орындалады. Бұл метрикалық кеңістікті
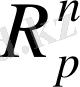 -
деп белгілейміз.
-
деп белгілейміз.
2)
 болғанда бұл кеңістік n-өлшемді арифметикалық
болғанда бұл кеңістік n-өлшемді арифметикалық
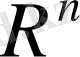 евклид кеңістігіне айналады.
евклид кеңістігіне айналады.
3) Барлық нақты сандардың шектелген тізбегін жиынын қарастырайық:
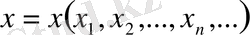 ,
,
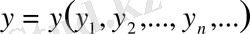 осы жиынның кез келген екі элементі болсын
осы жиынның кез келген екі элементі болсын
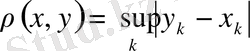
бұл метрика 1) - 3) аксиомаларды қанағаттандырады. Сондықтан аталған жиын метрикалық кеңістік болады, оны
 деп белгілейміз.
деп белгілейміз.
4)
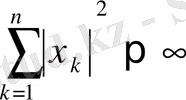 теңсіздігін қанағаттандыратын шексіз
теңсіздігін қанағаттандыратын шексіз
 сан тізбектерінің жиынын қарастырайық. Оны
сан тізбектерінің жиынын қарастырайық. Оны
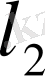 деп белгілейміз.
деп белгілейміз.
Осы жиында кез келген екі элементтің арақашықтығы
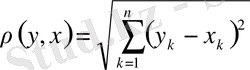
теңдігі арқылы анықтасақ ол метрикалық кеңістікке айналады. Ол үшін мынадай элементар теңсіздікті пайдаланамыз.
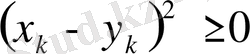
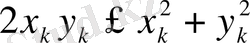

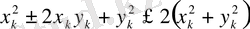
немесе
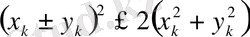
Соңғы теңсіздіктен
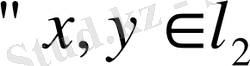 үшін
үшін
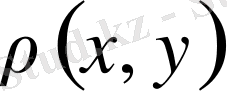 шамасының мағынасы бар болады, немесе
шамасының мағынасы бар болады, немесе
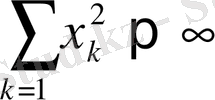
және
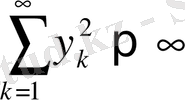

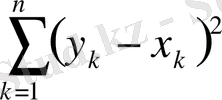
1) және 2) аксиомалардың орындалуы жеңіл дәлелденеді, ал 3) аксиома мына төмендегі теңсіздіктерден шығады (р=2 болғанда Миньковский теңсіздігі)
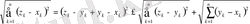
Бұл теңсіздікте
 шекке көшу арқылы мына теңсіздікті аламыз
шекке көшу арқылы мына теңсіздікті аламыз
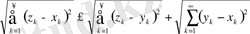
Бұл кеңістік
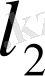 кеңістігі деп аталады.
кеңістігі деп аталады.
Дәл осы жолмен
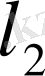 кеңістігін
кеңістігін
 -ге жалпылауға болады.
-ге жалпылауға болады.
Енді функционалдық метрикалық кеңістіктерге бірнеше мысалдар келтірейік
5)
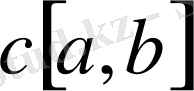 кеңістігі.
кеңістігі.
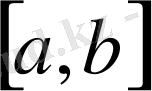 кесіндісінде анықталған үзіліссіз функциялар жиынында
кесіндісінде анықталған үзіліссіз функциялар жиынында
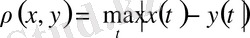
Метрикасын енгіземіз. Бұл үш аксиоманы да онай қанағаттандырады. Сондықтан
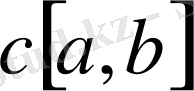 -метрикалық кеңістік,
-метрикалық кеңістік,
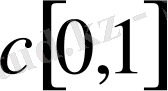 -ді
-ді
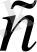 деп те белгілейміз.
деп те белгілейміз.
6)
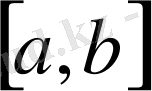 кесіндісінде анықталған үзіліссіз функциялар жиын, онда
кесіндісінде анықталған үзіліссіз функциялар жиын, онда
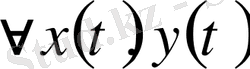 функцияларының арақашықтығы
функцияларының арақашықтығы
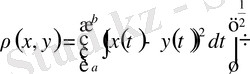
Бұл метрикалық кеңістік болады, оны
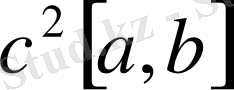 белгілейміз. 1), 2) аксиомалар оңай орындалады. 3) аксиома Миньковский интегралдық теңсіздігінен шығады. р=2 болғанда
белгілейміз. 1), 2) аксиомалар оңай орындалады. 3) аксиома Миньковский интегралдық теңсіздігінен шығады. р=2 болғанда
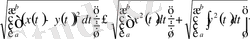
Метрикалық кеңістікті үзіліссіз бейнелеу
 ,
,
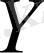 - екі метрикалық кеңістік болсын.
- екі метрикалық кеңістік болсын.
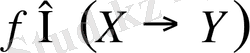
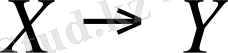 бейнелейтін болсын
бейнелейтін болсын
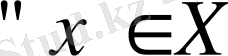 үшін
үшін
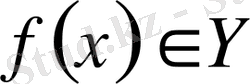
Анықтама:
 болсын
болсын
 үшін
үшін
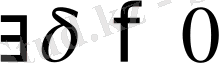
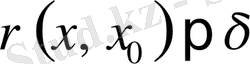 табылып,
табылып,
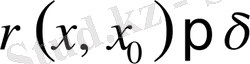

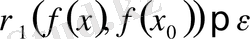 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
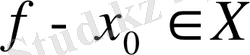 нүктесінде үзіліссіз бейнелеуі болады. (мұндағы
нүктесінде үзіліссіз бейнелеуі болады. (мұндағы
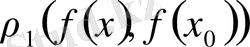
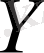 -де анықталған метрика)
-де анықталған метрика)
Мысал:
 - метрикалық кеңістік болсын.
- метрикалық кеңістік болсын.
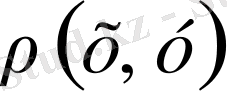
 -те анықталған метрика болсын. Егер
-те анықталған метрика болсын. Егер
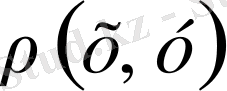 метрикасы
метрикасы
 -те анықталған екі айнымалы шамаға тәуелді деп қарастырсақ, ол функция да үзіліссіз ункция болады. Ол үшін 3)
-те анықталған екі айнымалы шамаға тәуелді деп қарастырсақ, ол функция да үзіліссіз ункция болады. Ол үшін 3)
 -тар аксиомасын мына түрде түрлендіреміз
-тар аксиомасын мына түрде түрлендіреміз
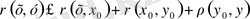

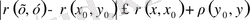
Бұл теңсідіктен
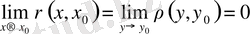 (1 аксиомадан шығады)
(1 аксиомадан шығады)
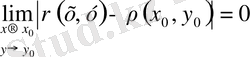
Бұл теңсіздік
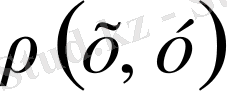 функциясын (метрикасын)
функциясын (метрикасын)
 - кеңістігінде үзіліссіз екенін көрсетеді.
- кеңістігінде үзіліссіз екенін көрсетеді.
1. 4. Гильберт кеңістігі
сызықты кеңістікті қарастырайық.
Анықтама 1. 4. 1.
Сызықты кеңістік (нақты, комплексті) гильберт кеңістігі деп аталады, егер ондағы кез келген
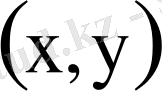 векторлар жұбы үшін төменгі аксиомаларды қанағаттандыратын
векторлар жұбы үшін төменгі аксиомаларды қанағаттандыратын
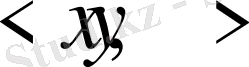 скаляр көбейтіндісі табылса:
скаляр көбейтіндісі табылса:
1)
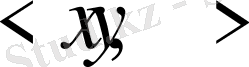 нақты немесе комплекс сан;
нақты немесе комплекс сан;
2)
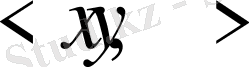 =
=

3)
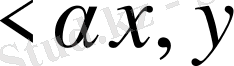 >
>
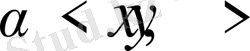
4)
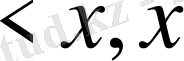 >
>
 , мұнда
, мұнда
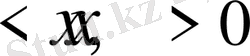
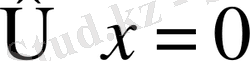 ;
;
5)
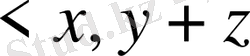 >=
>=
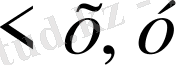 >+
>+
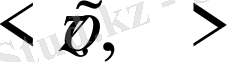 .
.
2) мен 3) -тен
 =
=
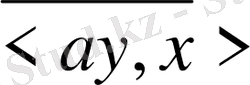 =
=
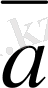 <
<
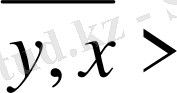
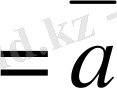
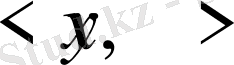 екендігі шығады.
екендігі шығады.
5) пен 2) -ден
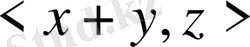 =
=
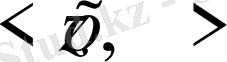 +
+
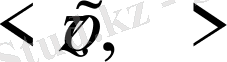 .
.
Гильберт кеңістігін Н деп белгілейміз. Егер норманы
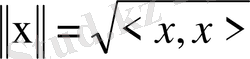 ретінде алсақ, онда Гильберт кеңістігі нормаланған болады.
ретінде алсақ, онда Гильберт кеңістігі нормаланған болады.
6) бұл норма бойынша Н толық кеңістік болады.
3), 4) аксиомалар бойынша
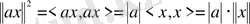 .
.
Кез келген Н кеңістігіндегі х, у элементтері үшін Коши-Буняковский теңсіздігі орындалады:
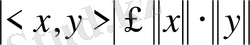 .
.
Гильберт кеңістігіне келесі мысалдарды келтірейік.
1- мысал.
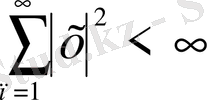
шартын қанағаттандыратын
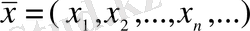 сандар (нақты немесе комплексті) тізбегі элементтері болатын
сандар (нақты немесе комплексті) тізбегі элементтері болатын
 кеңістігінде скалярлық көбейту
кеңістігінде скалярлық көбейту
формуласы бойынша анықталады. Бұл кеңістік гильберттік болады. Вектор нормасы мына
формуласы бойынша анықталады.
2-мысал.
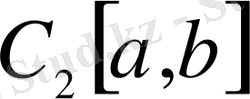 комплексті мәнді үздіксіз функциялар кеңістігі
комплексті мәнді үздіксіз функциялар кеңістігі
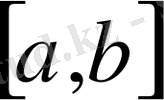 аралығында (кесіндісінде)
аралығында (кесіндісінде)
скалярлық көбейтіндісімен гильбертті кеңістік болады. Вектор нормасы
формуласы бойынша анықталады.
Гилберт кеңістігінің ортогонал жіктелуі . Н - Гильберт кеңістігі, Н 1 - оның (толық) ішкі кеңістігі болсын.
Теорема 1. 4. 2.
Кез-келген
 векторын
векторын
 элементі мен оған ортогонал
элементі мен оған ортогонал
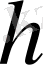 векторының қосындысына жіктеуге болады және
векторының қосындысына жіктеуге болады және
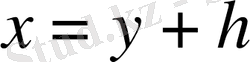 қосындысына
қосындысына
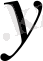 пен
пен
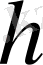 қосылғыштары жалғыз түрде ғана табылады.
қосылғыштары жалғыз түрде ғана табылады.
Дәлелдеуі.
Егер
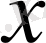 векторы Н
1
ішкеңістігінде жатса, онда
векторы Н
1
ішкеңістігінде жатса, онда
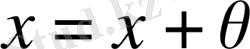 , яғни бұл
, яғни бұл
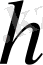 нөлдік векторға тең болатын мардымсыз жағдай. Енді
нөлдік векторға тең болатын мардымсыз жағдай. Енді
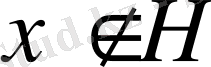 және
және
(*)
болсын. Инфимумның анықтамасы бойынша
 кезде
кезде
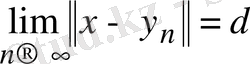 болатын
болатын
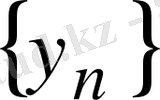 тізбегі табылады. Осы
тізбегі табылады. Осы
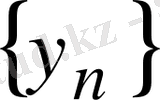 фундаменталь тізбек екенін дәлелдейік. Сол мақсатпен алдымен
фундаменталь тізбек екенін дәлелдейік. Сол мақсатпен алдымен
және
теңдіктерін ескере отырып,
 және
және
 векторларына параллелограмның диагоналдары туралы теореманы қолданайық:
векторларына параллелограмның диагоналдары туралы теореманы қолданайық:
,
осыдан,
(1. 4. 1)
Бұл (1. 4. 1) теңдігінің оң жағындағы алғашқы екі қосылғыштар (*) бойынша
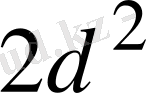 санынан кем емес, және
санынан кем емес, және
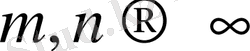 кезде, екеуі де осы
кезде, екеуі де осы
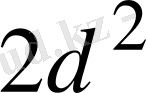 санына ұмтылады. Ал соңғы қосылғышта
санына ұмтылады. Ал соңғы қосылғышта
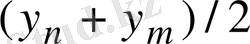 векторы
векторы
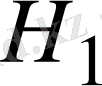 ішкеңістігінің элементі болғандықтан,
ішкеңістігінің элементі болғандықтан,
,
сондықтан,
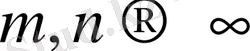 кезде
кезде
Демек,
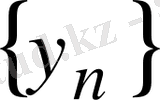 фундаменталь тізбек, ал
фундаменталь тізбек, ал
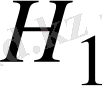 толық ішкеңістік болғандықтан,
толық ішкеңістік болғандықтан,
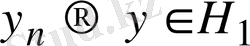 .
.
Енді
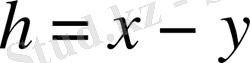 векторы
векторы
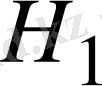 ішкеңістігіне ортогонал екенін дәлелдейік. Кез-келген
ішкеңістігіне ортогонал екенін дәлелдейік. Кез-келген
 векторы мен кез-келген
векторы мен кез-келген
 саны үшін
саны үшін
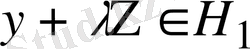 , демек,
, демек,
 -ға тәуелді
-ға тәуелді
квадраттық функцияның ең кіші мәні
 болғанда қабылданады. Сондықтан оның
болғанда қабылданады. Сондықтан оның
 нүктесінде туындысы
нүктесінде туындысы
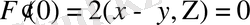 , яғни
, яғни
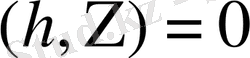 . Сонымен
. Сонымен
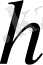 векторы кез-келген
векторы кез-келген
 векторына, демек,
векторына, демек,
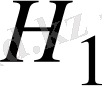 ішкеңістігіне ортогонал вектор. Осымен
ішкеңістігіне ортогонал вектор. Осымен
 векторының
векторының
 және оған ортогонал
және оған ортогонал
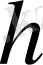 векторының қосындысына жіктелетіндігі дәлелденді.
векторының қосындысына жіктелетіндігі дәлелденді.
Енді
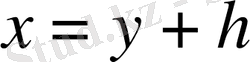 жіктелуінің бірмәнді екенін дәлелдеу үшін
жіктелуінің бірмәнді екенін дәлелдеу үшін
 және
және
 векторлары бар және
векторлары бар және
,
яғни
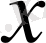 векторы екі түрде жіктелген деп жориық. Онда
векторы екі түрде жіктелген деп жориық. Онда
енді осы теңдіктің екі жағын
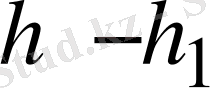 векторына скаляр көбейтейік:
векторына скаляр көбейтейік:
себебі
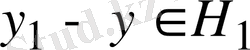 , ал
, ал
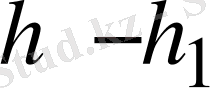 оған ортогонал вектор. Демек,
оған ортогонал вектор. Демек,
 , онан
, онан
 екені шығады. Осымен теорема толық дәлелденді.
екені шығады. Осымен теорема толық дәлелденді.
Ескерту.
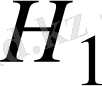 ішкеңістігіне ортогонал
ішкеңістігіне ортогонал
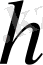 векторларының сызықтық комбинациясы, сонымен қатар, осындай векторлардың
векторларының сызықтық комбинациясы, сонымен қатар, осындай векторлардың
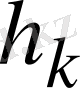 тізбегінің шегі 1- және 2- леммалара бойынша
тізбегінің шегі 1- және 2- леммалара бойынша
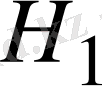 -ге ортогонал болғандықтан, олардың өзі ішкеңістік құрады. Бұл ішкеңістік
-ге ортогонал болғандықтан, олардың өзі ішкеңістік құрады. Бұл ішкеңістік
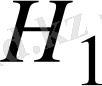 кеңістігінің ортогонал толықтауышы деп аталады. Егер
кеңістігінің ортогонал толықтауышы деп аталады. Егер
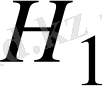 кеңістігіне ортогонал кеңістікті
кеңістігіне ортогонал кеңістікті
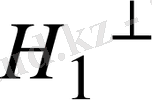 символымен белгілесек, онда дәлелденген теоремадан Н кеңістігінің өзара ортогонал екі ішкеңістіктің тік қосындысына жіктелетінін көреміз:
символымен белгілесек, онда дәлелденген теоремадан Н кеңістігінің өзара ортогонал екі ішкеңістіктің тік қосындысына жіктелетінін көреміз:
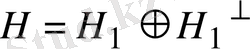 , немесе
, немесе
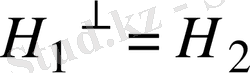 арқылы белгілесек, онда
арқылы белгілесек, онда
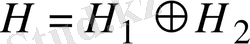 . Әр ішкеңістіктің өзін Гильберт кеңістігі ретінде қарап, дәлелденген теореманы әрі қарай қолданып, кез-келген натурал сан
. Әр ішкеңістіктің өзін Гильберт кеңістігі ретінде қарап, дәлелденген теореманы әрі қарай қолданып, кез-келген натурал сан
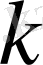 үшін
үшін
(1. 4. 2)
қосындысына жіктеуге болатыны айқын. Мұндағы
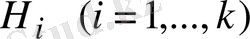 өзара ортогонал кеңістіктер. Қорытып айтқанда, Гильберт кеңістігін саны ақырлы ішкеңістіктердің ортогонал тік қосындысына жіктеуге болады екен. Осындай жағдайда кез-келген
өзара ортогонал кеңістіктер. Қорытып айтқанда, Гильберт кеңістігін саны ақырлы ішкеңістіктердің ортогонал тік қосындысына жіктеуге болады екен. Осындай жағдайда кез-келген
 векторы
векторы
(1. 4. 3)
түрінде жіктеледі және мұндағы
 .
.
1. 5.
 кеңістігі.
кеңістігі.
 белгісі арқылы
белгісі арқылы
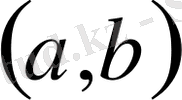 -да өлшемді,
-да өлшемді,
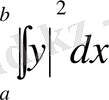 интегралы ақырлы болатын
интегралы ақырлы болатын
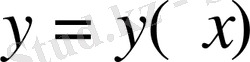 функциялар жиынын белгілейміз.
функциялар жиынын белгілейміз.
егер
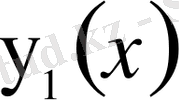 және
және
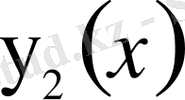 функциялары тек нөлдік өлшемді жиында ғана әртүрлі болса, онда олар тең деп қарастырылады. Мұнда өлшем мен интеграл Лебег мағынасында қарастырылады.
функциялары тек нөлдік өлшемді жиында ғана әртүрлі болса, онда олар тең деп қарастырылады. Мұнда өлшем мен интеграл Лебег мағынасында қарастырылады.
Егер
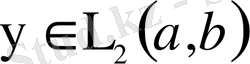 болса, онда у функциясы үшін
болса, онда у функциясы үшін
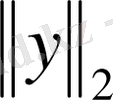 нормасы келесідей анықталады:
нормасы келесідей анықталады:
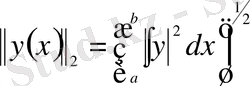 .
.
Бұл норма мынадай қасиеттерге ие:
1)
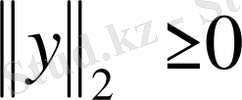 барлық у үшін,
барлық у үшін,
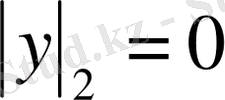 және
және
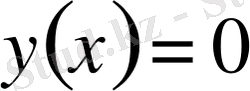 шарттары эквивалентті;
шарттары эквивалентті;
2)
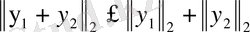
3)
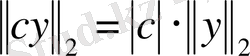 , мұндағы с - константа.
, мұндағы с - константа.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz