Ішек пен мембрананың көлденең тербелістері: шекаралық және бастапқы шарттар, есептердің жалпы құрылымы және бірегей шешім теоремасы


.
2. Мембрананың көлденең тербелісі.
3. Шекаралық және бастапқы шарттар.
4. Жалпы есептер құрылымы.
5. Бірғана (жалғыз) шешім теоремасы.
1. . Ішектің жәй көлденең тербелісі. Ұзындығы l ішектің t моментіндегі жағдайы
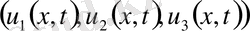 ығысу векторының х нүктесінің t моментіндегі орнымен анықталады. Ішек бір жазықтықта
ығысу векторының х нүктесінің t моментіндегі орнымен анықталады. Ішек бір жазықтықта
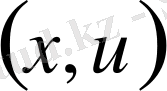 жатады десек, тербеліс үдерісі
жатады десек, тербеліс үдерісі
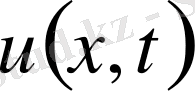 функциясымен анықталады. Ішекті икемді, серпінді деп қарастырамыз. Онда кернеулер дәл моменттегі кескінге жанама бағытында әсер етеді.
функциясымен анықталады. Ішекті икемді, серпінді деп қарастырамыз. Онда кернеулер дәл моменттегі кескінге жанама бағытында әсер етеді.
Сонымен
T(x) =T
 ішекті керу күш Ньютонның екінші заңы бойынша
ішекті керу күш Ньютонның екінші заңы бойынша
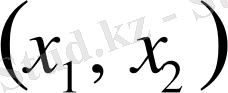 бөлігіндегі қозғалыс шамасы
бөлігіндегі қозғалыс шамасы
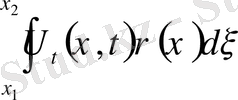 ,
,
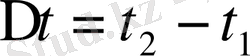 уақыт аралығындағы өзгерісі
уақыт аралығындағы өзгерісі
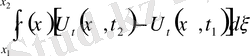 әсер етуші күштерге тең; яғни
әсер етуші күштерге тең; яғни
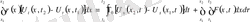 ) (1) . Теңдеу (1) ішектің көлденең тербелісінің интегралдық түрі. U(x, t)
) (1) . Теңдеу (1) ішектің көлденең тербелісінің интегралдық түрі. U(x, t)
 c
c
 дей отырып, интегралдың орта мәні туралы теореманы екі рет, ақырлы өсімшелер теоремасын бірге қолдансақ, ішек тербелісінің дифференциалдық теңдеуін аламыз
дей отырып, интегралдың орта мәні туралы теореманы екі рет, ақырлы өсімшелер теоремасын бірге қолдансақ, ішек тербелісінің дифференциалдық теңдеуін аламыз
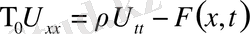 (2) ішектің тығыздығы
(2) ішектің тығыздығы
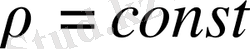 болғанда
болғанда
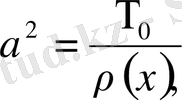 (3),
(3),
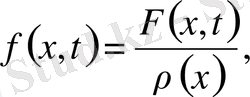 (4) Сыртқы әсер күші жоқ болса
(4) Сыртқы әсер күші жоқ болса
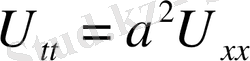 немесе
немесе
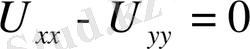 (
(
 ) теңдеуі шығады. х
) теңдеуі шығады. х
 нүктесінде l
нүктесінде l
 (t) шоғырланған күш әсерінде теңдеу (1) мына түрге енеді
(t) шоғырланған күш әсерінде теңдеу (1) мына түрге енеді
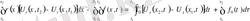 . Бұдан келесі орындалуы тиісті түйіндестік шарттарын аламыз:
. Бұдан келесі орындалуы тиісті түйіндестік шарттарын аламыз:
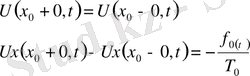 (5)
(5)
2. Мембрананың көлденең тербелісі Иілгіш және ығыстыруға кедергі жасамайтын жазық қолбырды, мембрана деп атайды. C-контурмен шектелген мембрана қарастырылады.
Мембрана үстіндегі
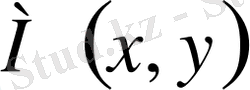 нүктесінен өтетін ds доғасына әсер етуші тарту күші Tds,
нүктесінен өтетін ds доғасына әсер етуші тарту күші Tds,
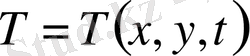 . Сыртқы әсер күші
. Сыртқы әсер күші
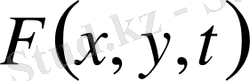 . Қозғалыс шамасының өзгеруін тартылыс күшінің вертикалдық жасаушысы мен сыртқы әсер күшінің қосындысына теңестіріп, мембрана тербелісінің интегралдық түрін аламыз
. Қозғалыс шамасының өзгеруін тартылыс күшінің вертикалдық жасаушысы мен сыртқы әсер күшінің қосындысына теңестіріп, мембрана тербелісінің интегралдық түрін аламыз
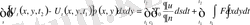 (6),
(6),
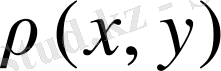 -мембрананың беттік тығыздығы.
-мембрананың беттік тығыздығы.
Дифференциалдық теңдеуге көшу үшін
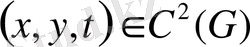 класынан деп, Остроградский теоремасын қолданамыз
класынан деп, Остроградский теоремасын қолданамыз
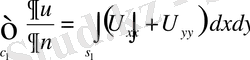 .
.
Онда интегралдық теңдеу (6) келесі түрге келтіріліп
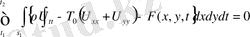 , орта мән туралы теореманың нәтижесінде мембрана тербелісінің дифференциалдық теңдеуін аламыз
, орта мән туралы теореманың нәтижесінде мембрана тербелісінің дифференциалдық теңдеуін аламыз
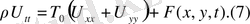 Біртекті мембрана үшін
Біртекті мембрана үшін
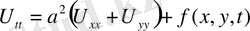
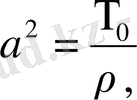 , (8)
, (8)
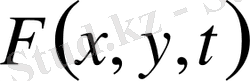 -мембрана массасы бірлігіне бөлінген күш тығыздығы.
-мембрана массасы бірлігіне бөлінген күш тығыздығы.
3. Шекаралық және бастапқы шарттар Физикалық есеп дифференциалдық теңдеуге келтірілгенде, үдерісті бір мәнді сипаттау қажеттілігі үшін қосымша шарттар қойылады. Бұл шарттар бастапқы және шекаралық болып келеді.
Ішектің шеткі нүктелері
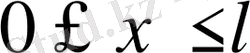 бекітілгенде
бекітілгенде
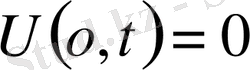 ,
,
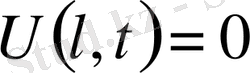 (9) шарттары қойылу мүмкін. Тербеліс үдерісі ішектің бастапқы жағдайынан тәуелділігі
(9) шарттары қойылу мүмкін. Тербеліс үдерісі ішектің бастапқы жағдайынан тәуелділігі
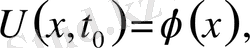
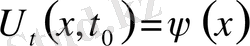 (10) түрінде қойылу мүмкін, бұлар бастапқы шарттар делінеді. Нақты жағдайға байланысты осы сияқты әртүрлі бастапқы және шекаралық қосымша шарттар қойылады.
(10) түрінде қойылу мүмкін, бұлар бастапқы шарттар делінеді. Нақты жағдайға байланысты осы сияқты әртүрлі бастапқы және шекаралық қосымша шарттар қойылады.
Негізінен келесі үш түрлі шекаралық шарттар қойылады:
бірінші түрдегі шекаралық шарт
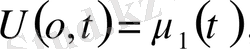
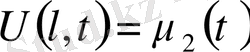 -берілген режим;
-берілген режим;
екінші түрдегі шекаралық шарт
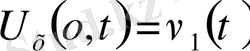 ,
,
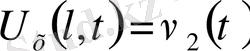 -берілген күш;
-берілген күш;
үшінші шекаралық шарт
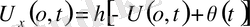 ,
,
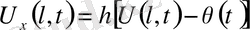 -серпінді бекіту.
-серпінді бекіту.
Күрделі және аралас түрдегі шекаралық шарттар да қойылуы мүмкін.
Шекаралық шарттың түріне байланысты қойылатын есептер шекаралық немесе шеттік есептер деп аталады.
Бірінші шеттік есептің қойылуы:
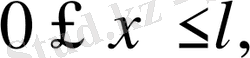
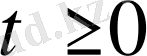 облысында анықталған, теңдеуді
облысында анықталған, теңдеуді
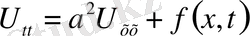
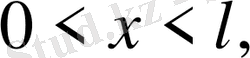
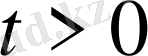 , шекаралық шарттарды
, шекаралық шарттарды
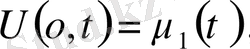
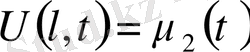
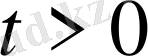 және бастапқы шарттарды
және бастапқы шарттарды
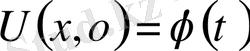 ,
,
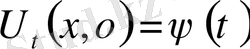
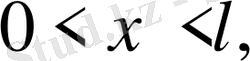 қанағаттандыратын
қанағаттандыратын
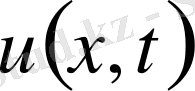 функциясын табу керек.
функциясын табу керек.
Дәл осылайша екінші шекаралық шартпен екінші, үшінші шекаралық шартпен үшінші шеттік есептер қойылады.
Шектеусіз
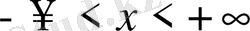 облыста бастапқы шарт ғана берілу мүмкін. Мұндай есепті бастапқы шартты немесе Коши есебі деп атайды: Теңдеудің
облыста бастапқы шарт ғана берілу мүмкін. Мұндай есепті бастапқы шартты немесе Коши есебі деп атайды: Теңдеудің
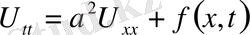 ,
,
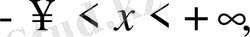
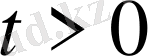 бастапқы шарттарды
бастапқы шарттарды
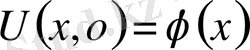 ,
,
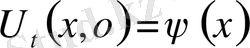 ,
,
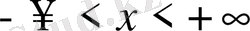 қанағаттандыратын шешімін табу керек.
қанағаттандыратын шешімін табу керек.
Оператор
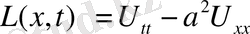 енгізсек, теңдеу L(x, t) =f(x, t) (11) түрінде жазылады. Онда жарты түзу
енгізсек, теңдеу L(x, t) =f(x, t) (11) түрінде жазылады. Онда жарты түзу
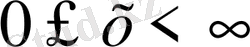 есептері былай қойылуы мүмкін:
есептері былай қойылуы мүмкін:
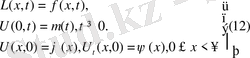 ,
,
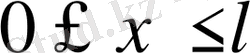
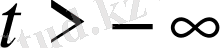 :
:
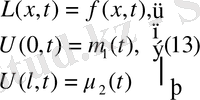 бастапқы шартсыз есеп.
бастапқы шартсыз есеп.
4. Күрделі есепті жәй есептерге жіктеп, жәй есептер шешімдерінен күрделі есеп шешімін құру көп жағдайда тиімді. Жалпы есеп шешімін
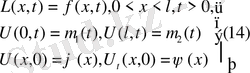 мына түрде іздестіреміз
мына түрде іздестіреміз
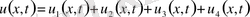 , (15) oнда
, (15) oнда
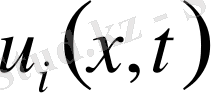 -тер келесі шеттік есептердің шешімдері
-тер келесі шеттік есептердің шешімдері
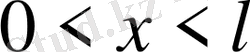 , t>0
, t>0
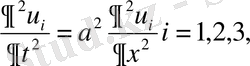
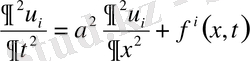
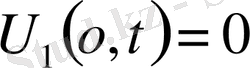 ,
,
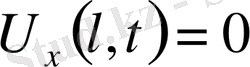 ,
,
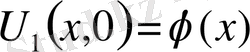 ,
,
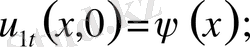
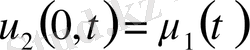
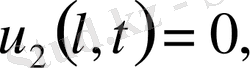
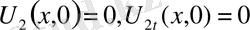 ,
,
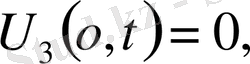
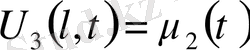 ,
,
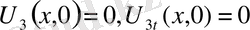 ,
,
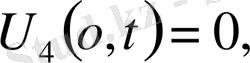
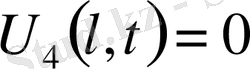 ,
,
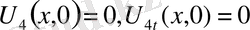
Жалпы шеттік есеп үшін де осындай әрекеттер жасау мүмкін.
Геометриялық айнымалылар саны n>1 болғанда да есептер осылайша қойылады:
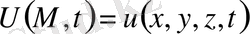 функциясын
функциясын
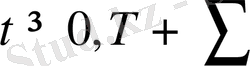 облысы ішінде анықталған,
облысы ішінде анықталған,
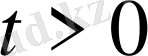 T-ішкі нүктелерінде теңдеуді
T-ішкі нүктелерінде теңдеуді
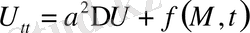
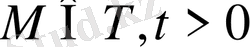 (16) қанағаттандыратын,
(16) қанағаттандыратын,
 шекарасында шекаралық шартты орындайтын
шекарасында шекаралық шартты орындайтын
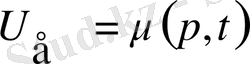
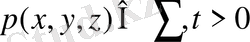 (17)
(17)
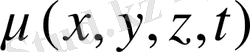 шекарада
шекарада
 берілегн функция және бастапқы(алғашқы) шарттарды орындайтын
берілегн функция және бастапқы(алғашқы) шарттарды орындайтын
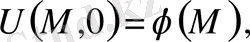
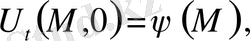 (18) табу керек. Есеп шектеусіз облыстар үшін де осыған ұқсас қойылады.
(18) табу керек. Есеп шектеусіз облыстар үшін де осыған ұқсас қойылады.
5. Бір ғана шешім теоремасы
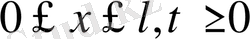 облысында анықталған, теңдеуді
облысында анықталған, теңдеуді
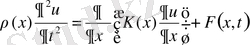
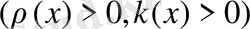
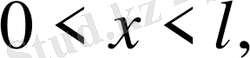
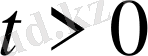 (19) бастапқы және шекаралық шарттарды қанағаттандыратын бір ғана функцияның бар болуы мүмкін, егер келесі шарттар орындалса:
(19) бастапқы және шекаралық шарттарды қанағаттандыратын бір ғана функцияның бар болуы мүмкін, егер келесі шарттар орындалса:
1) функция
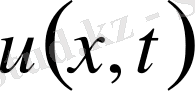 және теңдеудегі (19) туындыларымен бірге
және теңдеудегі (19) туындыларымен бірге
 туындысы да
туындысы да
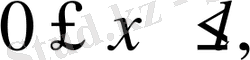
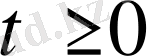 облысында үздіксіз болса;
облысында үздіксіз болса;
2) коэффициенттері
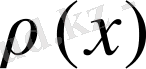 және
және
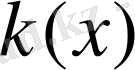 кесіндіде
кесіндіде
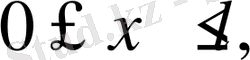 үздіксіз болса.
үздіксіз болса.
Дәлелдеуі
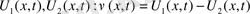 шешімдері делік. Онда
шешімдері делік. Онда
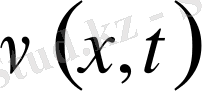 :
:
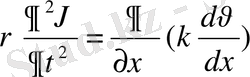 ,
,
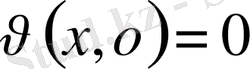 ,
,
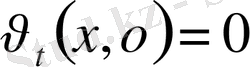 ;
;
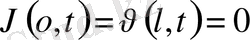 .
.
Функция
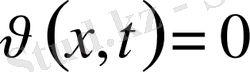 екендігіне көз жеткізелік.
екендігіне көз жеткізелік.
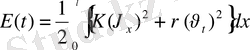 функциясы ішектің t моментігіндегі толық энергиясы.
функциясы ішектің t моментігіндегі толық энергиясы.
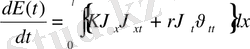 , (
, (
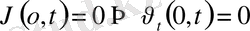 және x=l мәнінде)
және x=l мәнінде)
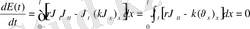 , яғни
, яғни
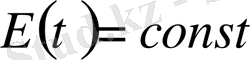 . Бастапқы шарттардан
. Бастапқы шарттардан
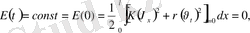 .
.
себебі
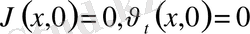 . Соңғы формуладан
. Соңғы формуладан
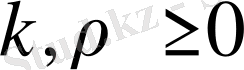 болғандықтан
болғандықтан
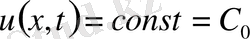 бастапқы шарттан
бастапқы шарттан
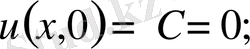 демек
демек
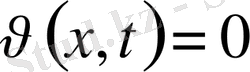 .
.
Егер
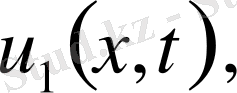
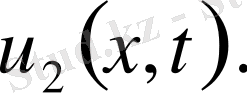 функциялары теорема шарттарын орындаса, онда
функциялары теорема шарттарын орындаса, онда
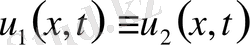 теорема дәлелденді.
теорема дәлелденді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz