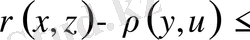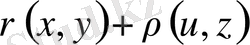Сызықты кеңістіктер: анықтамалар, нормаланған және метрикалық құрылымдар, сызықты операторлар


I БӨЛІМ
1. 1 СЫЗЫҚТЫ КЕҢІСТІКТЕР
1 . 1. 1 Сызықтық кеңістік ұғымы
Анықтама 1. 1. 1
Егер қайсыбір
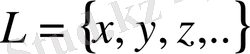 жиынында:
жиынында:
1. Кез-келген
 элементтері үшін олардың қосындысы деп аталатын мына қасиеттер орындалса:
элементтері үшін олардың қосындысы деп аталатын мына қасиеттер орындалса:
- үшінтеңдігі орындалатын бір ғанаэлементі бар болуы ( нөлдік элемент) ;
- үшінтеңдігі орындалатынэлементі бар және ол әрүшін біреу ғана болса және
2. Кез келген
 және кез келген
және кез келген
 нақты саны үшін
нақты саны үшін
 элементі мен
элементі мен
 санының көбейтіндісі деп аталатын
санының көбейтіндісі деп аталатын
 элементі анықталған болса және бұл элементті санға көбейту амалы мен элементтерді қосу амалдары мына төмендегі шарттарды қанағаттандыратын болса.
элементі анықталған болса және бұл элементті санға көбейту амалы мен элементтерді қосу амалдары мына төмендегі шарттарды қанағаттандыратын болса.
1)
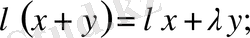
2)
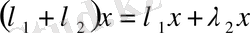
3)
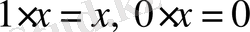
4)
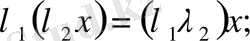
Онда бұл
 жиыны
сызықты кеңістік
депе аталады.
жиыны
сызықты кеңістік
депе аталады.
 жиынының элементерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады.
жиынының элементерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады.
 жиынының элементтері көбейтілетін сандар жиыны
жиынының элементтері көбейтілетін сандар жиыны
 алынуына қарай нақты сызықтық кеңістік, немесе комплекс сызықтық кеңістік пайда болады.
алынуына қарай нақты сызықтық кеңістік, немесе комплекс сызықтық кеңістік пайда болады.
Егер
 жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалатыны жақсы белгілі. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар орындалатыны (аналитикалық геометриядан) белгілі. Демек, әдеткі амалдар анықталған сандар жиыны, немесе векторлар жиыны
сызықтық кеңістіктің мысалдары болып табылады.
жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалатыны жақсы белгілі. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар орындалатыны (аналитикалық геометриядан) белгілі. Демек, әдеткі амалдар анықталған сандар жиыны, немесе векторлар жиыны
сызықтық кеңістіктің мысалдары болып табылады.
Сонымен, қайсыбір жиында кез-келген екі элементтің қосындысы және элементтің нақты (комплекс) санға көбейтіндісі анықталса және бұл амалдар жоғарыдағы аксиомаларды қанағаттандырса, онда бұл жиын сызықтық кеңістікке айналады.
1-мысал.
Барлық мүмкін векторлар жиыны (үш өлшемді кеңістікте, жазықтықта немесе түзуде) сызықты кеңістікті жасайды. Вектордың қосындысы параллелограммның ережесі бойынша анықталатынын, ал
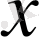 векторының нақты
векторының нақты
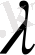 санына көбейтіндісі
санына көбейтіндісі
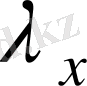 векторы арқылы анықталатынын еске түсіреміз, оның ұзындығы
векторы арқылы анықталатынын еске түсіреміз, оның ұзындығы
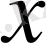 ұзындығына
ұзындығына
 көбейтіндісі, ал бағыты
көбейтіндісі, ал бағыты
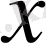 бағытына дәл келеді, егер
бағытына дәл келеді, егер
 және оған қарама-
және оған қарама-
қарсы
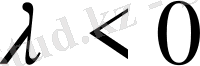 болса. Сызықты кеңістіктің аксиомалары - бұл векторлармен атақты операция қасиеттері.
болса. Сызықты кеңістіктің аксиомалары - бұл векторлармен атақты операция қасиеттері.
Осылайша, сызықты кеңістіктің элементтері міндетті түрде жалпыланған векторлар ретінде қарастырылады. «Сызықты кеңістік» терминінің орнына «векторлық кеңістік» термині де қолданылады. Ары қарай, сызықты кеңістіктің элементтерін айтқанда, біз оны вектор деп те атайтын боламыз.
2-мысал.
 жиынын барлық мүмкін нақты сандарынан реттелген терулермен қарастырамыз.
жиынын барлық мүмкін нақты сандарынан реттелген терулермен қарастырамыз.
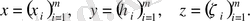
 сандарын
сандарын
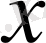 бағандарының координаталары деп атаймыз.
бағандарының координаталары деп атаймыз.
 бағандарының қосындысынан бағанды түсінетін боламыз, олардың координаталары -
бағандарының қосындысынан бағанды түсінетін боламыз, олардың координаталары -
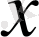 және
және
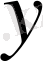 бағандарына сәйкес келетін координата, яғни
бағандарына сәйкес келетін координата, яғни
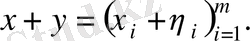
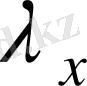 бағаннан
бағаннан
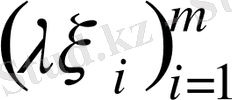 бағанын түсінетін боламыз, мұндағы
бағанын түсінетін боламыз, мұндағы
 - нақты сан. Нөлдің рөлін
- нақты сан. Нөлдің рөлін
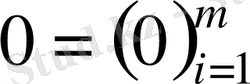 бағаны ойнайды. Бағандар операциясы координаттар операциясына, яғни сызықты кеңістік аксиомалары тривиальді орындалатын нақты сандарға келтірілетіндіктен, осы аксиомалар бағандарға да орындалады. Осылайша,
бағаны ойнайды. Бағандар операциясы координаттар операциясына, яғни сызықты кеңістік аксиомалары тривиальді орындалатын нақты сандарға келтірілетіндіктен, осы аксиомалар бағандарға да орындалады. Осылайша,
 сызықты кеңістік болып табылады.
сызықты кеңістік болып табылады.
Комплекстік сандар бағандарын комплекстік сандарға көбейтіп қарастыруға болады. Қорыта келгенде бағандардың комплексті сызықты кеңістігін аламыз.
Енді функцияның сызықты кеңістігіне мысал қарастырамыз. Алдымен кейбір жалпы ескертулер жасаймыз.
 - кез келген табиғаттың кейбір
- кез келген табиғаттың кейбір
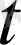 жиынының элементтері және әрбір
жиынының элементтері және әрбір
 -ға Е сызықты кеңістігінде
-ға Е сызықты кеңістігінде
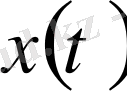 элементі сәйкес қойылған болсын, яғни
элементі сәйкес қойылған болсын, яғни
 анықталған облысында
анықталған облысында
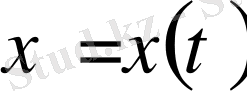 функциясы және Е-де облыстың мәндері берілген.
функциясы және Е-де облыстың мәндері берілген.
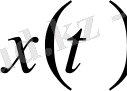 және
және
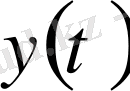 екі функцияның
екі функцияның
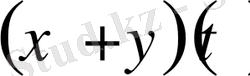 қосындысынан
қосындысынан
 функциясын түсінетін боламыз.
функциясын түсінетін боламыз.
 функциясын
функциясын
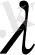 санына
санына
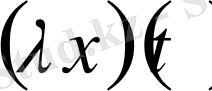 көбейтіндісінен
көбейтіндісінен
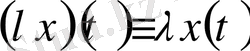 функциясын түсінетін боламыз.
функциясын түсінетін боламыз.
Төменде ұсынылған мысалдарда нақты немесе комплексті мәнді функция қарастырылған, Е - нақты ось немесе комплексті жазықтық. 2 мысалдағысияқы, осындай функциялардың операциясы нақты немесе комплексті сандар операциясына жинақталады.
 деп белгілеп және сол немесе басқа функциялар классын таңдай отырып, біз автоматты түрде сызықты кеңістіктің аксиомаларының орындалуын аламыз, егер тек
деп белгілеп және сол немесе басқа функциялар классын таңдай отырып, біз автоматты түрде сызықты кеңістіктің аксиомаларының орындалуын аламыз, егер тек
 және
және
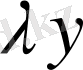 таңдалынған функциялар классына
таңдалынған функциялар классына
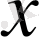 және
және
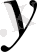 -пен бірге жататын болса.
-пен бірге жататын болса.
3-мысал.
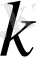 -дан асып кетпейтін, барлық дәрежелік көпмүшеліктің жиынтығын қарастырамыз:
-дан асып кетпейтін, барлық дәрежелік көпмүшеліктің жиынтығын қарастырамыз:
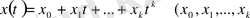 - кез келген нақты сан,
- кез келген нақты сан,
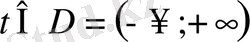 ) . Көпмүшелікті нақты санға көбейтіндісі және екі көпмүшеліктің қосындысы көпмүшеліктер болғандықтан, біз көпмүшеліктің сызықты кеңістігін аламыз.
) . Көпмүшелікті нақты санға көбейтіндісі және екі көпмүшеліктің қосындысы көпмүшеліктер болғандықтан, біз көпмүшеліктің сызықты кеңістігін аламыз.
Дәл осылайша
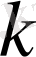 -дан асып кетпейтін комплексті сызықты кеңістіктегі дәрежелік көпмүшелікті қарастыруға болады. Оның
-дан асып кетпейтін комплексті сызықты кеңістіктегі дәрежелік көпмүшелікті қарастыруға болады. Оның
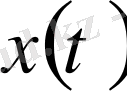 элементтері мынадай түрде болады
элементтері мынадай түрде болады
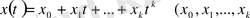 -комплексті сан,
-комплексті сан,
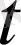 -
-
 комплексті жазықтығында өзгеретін, комплексті айнымалы) .
комплексті жазықтығында өзгеретін, комплексті айнымалы) .
4-мыса л.
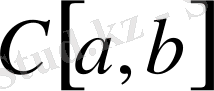 кеңістігі - үзіліссіз функциялардың кеңістігі. Айталық,
кеңістігі - үзіліссіз функциялардың кеңістігі. Айталық,
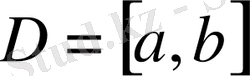 болсын.
болсын.
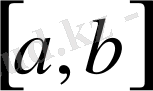 -да үзіліссіз барлық мүмкін
-да үзіліссіз барлық мүмкін
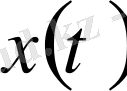 ,
,
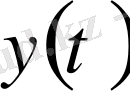 функцияларын аламыз.
функцияларын аламыз.
 -да
-да
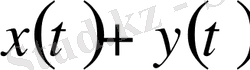 үзіліссіз және үзіліссіз функциялардың қосындысы ретінде
үзіліссіз және үзіліссіз функциялардың қосындысы ретінде
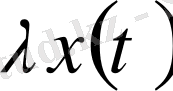 -да үзіліссіз болса, онда
-да үзіліссіз болса, онда
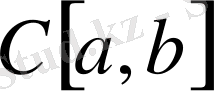 сызықты кеңістік болып табылады. Нақты және комплексті жағдайлар мүмкін.
сызықты кеңістік болып табылады. Нақты және комплексті жағдайлар мүмкін.
5-мысал.
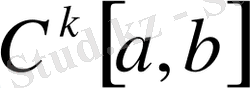 (
(
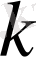 - натурал сан) кеңістігі -
- натурал сан) кеңістігі -
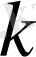 -ші ретті үзіліссіз дифференциалданатын функция кеңістігі
-ші ретті үзіліссіз дифференциалданатын функция кеңістігі
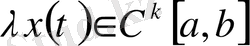 болғандықтан, егер
болғандықтан, егер
 және
және
 , егер
, егер
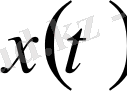 және
және
 болса, онда
болса, онда
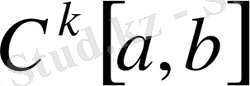 - сызықты кеңістік.
- сызықты кеңістік.
6-мысал
. Скалярлық элементтері арқылы
 ретпен барлық тіктөртбұрышты матрицалық
ретпен барлық тіктөртбұрышты матрицалық
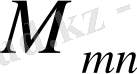 жиынын қарастырамыз.
жиынын қарастырамыз.
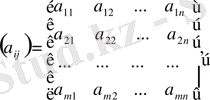
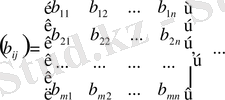
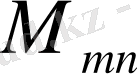 операциясын анықтаймыз
операциясын анықтаймыз
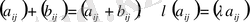
Матрицалардан алынған операция сандардан алынған операцияға жинайтын болса, онда аксиоманың дұрыстығы белгілі. Егер матрицаның және
 скалярларының элементтері нақты (комплексті) болса, онда біз нақты (комплексті) сызықты кеңістікке келеміз.
скалярларының элементтері нақты (комплексті) болса, онда біз нақты (комплексті) сызықты кеңістікке келеміз.
Анықтама 1. 1. 1(а)
Егер әрбір
 үшін нақты сан мәнді
үшін нақты сан мәнді
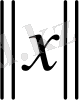 функциясы анықталса және ол мынана шарттарды қанағаттандыратын болса:
функциясы анықталса және ол мынана шарттарды қанағаттандыратын болса:
- және текболғанда ғана( норманың теріс еместік шарты) ;
- Кез келгенсаны үшін(норманың біртектілік шарты) ;
- Кез келгенүшін( үшбұрыш теңсіздігі),
Онда
кеңістігінде норма анықталған дейміз.
Норма анықталған сызықтық кеңістік нормаланған сызықтық кеңістік деп аталады.
1. 1. 2 Нормаланған сызықтық кеңістіктің мысалдары
1.
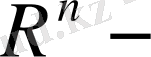 нормаланған сызықты кеңістікке айналдырамыз. Мұнда жатқан әрбір элемент
нормаланған сызықты кеңістікке айналдырамыз. Мұнда жатқан әрбір элемент
 үшін норманы
үшін норманы
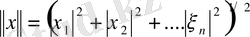 (1. 1. 1)
(1. 1. 1)
теңдігімен анықтаймыз. Осылай анықталған норма норманың аксиомаларын қанағаттандыратынын тексеру қажет. Бірінші шарттың орындалатыны (1) теңдігінің оң жағындағы өрнек көрер көзге теріс емес екендігінен айқын. Оны әрі, егер
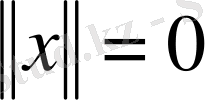 болса, онда барлық
болса, онда барлық
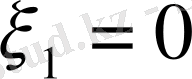 болғаны. Себебі, егер қайсібір
болғаны. Себебі, егер қайсібір
 болса, онда (1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын. Сонымен, егер
болса, онда (1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын. Сонымен, егер
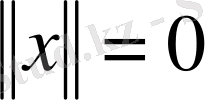 болса, онда
болса, онда
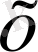 векторының барлық координаттары нөлге тең:
векторының барлық координаттары нөлге тең:
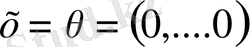 . Керісінше, егер
. Керісінше, егер
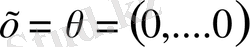 болса, онда
болса, онда
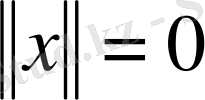 екені айқын.
екені айқын.
Екінші аксиома оңай тексеріледі.
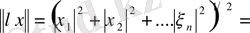
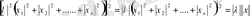 . (1. 1. 2)
. (1. 1. 2)
Үшінші аксиома, яғни үшбұрыш теңсіздігі орындалатынын дәлелдеу үшін алдымен Коши теңсіздігін еске алайық. Кез келген
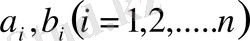 нақты сандар үшін
нақты сандар үшін
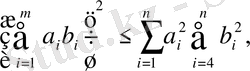 (1. 1. 3)
(1. 1. 3)
теңсіздігі орындалады. Бұл теңсіздіктің екі жағынан квадрат түбір алып, оны мына түрде де жазуға болады:
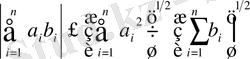 (1. 1. 4)
(1. 1. 4)
Енді осы теңсіздікті пайдаланып, (1) нормасы үшін үшбұрыш теңсіздігін дәлелдейік:
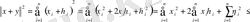

Теңсіздіктің екі жағынан квадрат түбір алып, үшбұрыш теңсіздігіне келеміз.
Сонымен (1. 1. 1) теңдігінен анықталған норма шынында да норма аксиомаларын қанағаттандыратыны айқын болды.
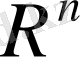 жиыны нормаланған сызықтық кеңістікке айналды. Бұл кеңістік, әдетте,
арифметикалық
Евклид кеңістігі
деп, ал норма (1. 1. 1) - Евклид нормасы деп аталады.
жиыны нормаланған сызықтық кеңістікке айналды. Бұл кеңістік, әдетте,
арифметикалық
Евклид кеңістігі
деп, ал норма (1. 1. 1) - Евклид нормасы деп аталады.
2.
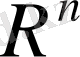 сызықтық кеңістігінде норманы басқаша, атап айтқанда,
сызықтық кеңістігінде норманы басқаша, атап айтқанда,
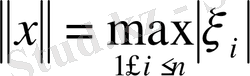 (1. 1. 5)
(1. 1. 5)
Теңдігі арқылы енгізіп, сол жиында анықталған тағы бір нормаланған сызықтық кеңістікке келеміз. Норманың аксиомалары орындалатынын тексеру бұл жолы тіпті оңай. Шынында да, (1. 1. 5) өрнегінен норманың теріс сан болмайтыны айқын және
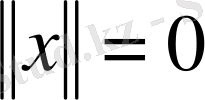 болуы барлық
болуы барлық
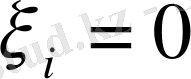 болғанда, тек қана осы жағдайда болады, яғни
болғанда, тек қана осы жағдайда болады, яғни
 .
.
Сондай-ақ, екінші, үшінші аксиомалардың тексерілуі де қиын емес:
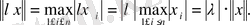 (1. 1. 6)
(1. 1. 6)
Егер
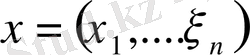 және
және
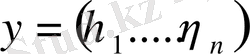 кеңістіктің кез - келген екі векторы болса, онда
кеңістіктің кез - келген екі векторы болса, онда
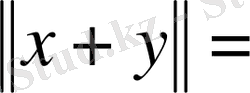
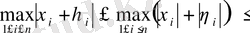
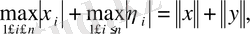
яғни үшбұрыш теңсіздігі орындалады екен.
Осы анықталған нормаланған сызықтық кеңістікті
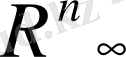 түрінде таңбалайтын боламыз.
түрінде таңбалайтын боламыз.
3
.
 символымен сол
символымен сол
 сызықтық кеңістігінде норманы
сызықтық кеңістігінде норманы
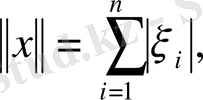 (1. 1. 7)
(1. 1. 7)
теңдігімен анықтау нәтижесінде пайда болған нормаланған сызықтық кеңістікті белгілейміз.
4.
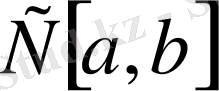 сызықтық кеңістігіндегі
сызықтық кеңістігіндегі
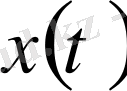 функциясының нормасы
функциясының нормасы
 (1. 1. 8)
(1. 1. 8)
теңдігімен анықталады.
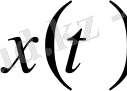 функциясы
функциясы
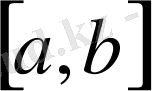 кесіндісінде үзіліссіз болғандықтан, оның модулі де үзіліссіз, демек, оның осы кесіндіде максимумы бар, сондықтан (1. 1. 8) теңдігі
кесіндісінде үзіліссіз болғандықтан, оның модулі де үзіліссіз, демек, оның осы кесіндіде максимумы бар, сондықтан (1. 1. 8) теңдігі
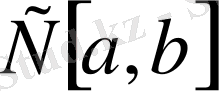 жиынының әрбір элементі
жиынының әрбір элементі
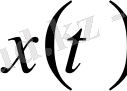 үшін оның нормасының мәнін бірмәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
үшін оның нормасының мәнін бірмәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
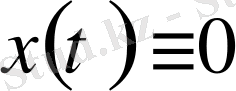 екендігі түсінікті. Сонымен бірінші аксиоманың орындалуы айқын. Енді
екендігі түсінікті. Сонымен бірінші аксиоманың орындалуы айқын. Енді
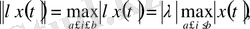 (1. 1. 9)
(1. 1. 9)
теңдігімен
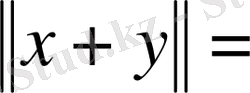
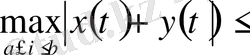
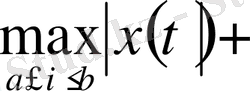
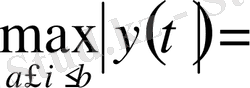
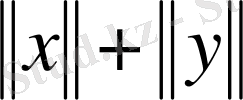 (1. 1. 10)
(1. 1. 10)
теңсіздігі норманың қалған екі аксиомасы да орындалатынын көрсетеді.
5.
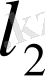 кеңістігі
кеңістігі
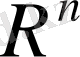 кеңістігінің
кеңістігінің
 жағдайына жалпыламасы. Бұл кеңістікті құрайтын
жағдайына жалпыламасы. Бұл кеңістікті құрайтын
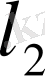 жиынының элементтері
жиынының элементтері
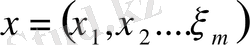 ,
,
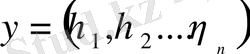 т. с. с, яғни, басқаша айтқанда бұл жиынның әр элементін координаттары саналымды вектор ретінде қарастыруға болады.
т. с. с, яғни, басқаша айтқанда бұл жиынның әр элементін координаттары саналымды вектор ретінде қарастыруға болады.
Енді осы жиында норма енгізілсе, нормаланған сызықтық кеңістік пайда болмақ.
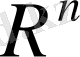 кеңістігінде норма
кеңістігінде норма
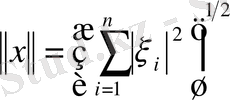
теңдігімен анықталып еді. Бірақ бұл формула қазіргі
 жағдайында кез келген
жағдайында кез келген
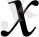 векторы үшін норманың сан мәнін анықтай алмайды. Сондықтан
векторы үшін норманың сан мәнін анықтай алмайды. Сондықтан
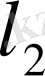 жиынына координаттары
жиынына координаттары
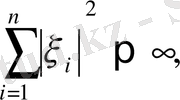 (1. 1. 11)
(1. 1. 11)
шартын қанағаттандыратын векторлар ғана енеді. Енді осы шартқа сай векторлар үшін норма
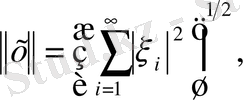 (1. 1. 12)
(1. 1. 12)
теңдігімен анықталады. Бұл анықтамаға еніп тұрған қатар шарты бойынша жинақты қатар, демек (12) өрнегі норманың сан мәнін анықтайды.
6.
 (шенелген тізбектер кеңістігі)
. Бұл кеңістікті құрайтын жиын элементтері сандар тізбегі арқылы анықталады. Мұнда осы векторларға қойылатын шарт - олардың координаттарының тізбегі шенелген тізбек болуы, яғни, егер
(шенелген тізбектер кеңістігі)
. Бұл кеңістікті құрайтын жиын элементтері сандар тізбегі арқылы анықталады. Мұнда осы векторларға қойылатын шарт - олардың координаттарының тізбегі шенелген тізбек болуы, яғни, егер
 болса, онда осы элементтке сәйкес С саны табылып кез келген
болса, онда осы элементтке сәйкес С саны табылып кез келген
 нөмірі үшін
нөмірі үшін
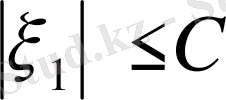 шарты орындалуы.
шарты орындалуы.
Енді осы жиынның кез келген
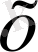 элементінің нормасын
элементінің нормасын
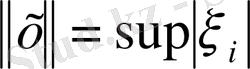 , (1. 1. 13)
, (1. 1. 13)
теңдігімен анықтаймыз. Шенелген
 тізбегінің супремумы ақырлы нақты сан, демек (1. 1. 13) теңдігі норманың сан мәнін бірмәнді анықтайды.
тізбегінің супремумы ақырлы нақты сан, демек (1. 1. 13) теңдігі норманың сан мәнін бірмәнді анықтайды.
7.
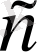 әріпі арқылы жинақты тізбектер жиынын белгілейік. Әрбір жинақты тізбек шенеулі болғандықтан,
әріпі арқылы жинақты тізбектер жиынын белгілейік. Әрбір жинақты тізбек шенеулі болғандықтан,
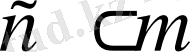 .
Екі жинақты тізбектің қосындысы және жинақты тізбектің тұрақты санға көбейтіндісі -- жинақты тізбек, демек,
.
Екі жинақты тізбектің қосындысы және жинақты тізбектің тұрақты санға көбейтіндісі -- жинақты тізбек, демек,
 жиынында анықталған норма оны нормаланған сызықты кеңістікке айналдырады.
жиынында анықталған норма оны нормаланған сызықты кеңістікке айналдырады.
8.
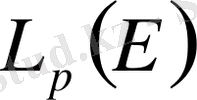 -
Лебег кеңістігі. Е жиынында қосындыланатын функциялардың жиыны сызықтық кеңістік құрайды. Бұл кеңістік
-
Лебег кеңістігі. Е жиынында қосындыланатын функциялардың жиыны сызықтық кеңістік құрайды. Бұл кеңістік
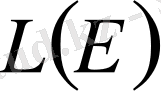 түрінде таңбаланады. Енді
түрінде таңбаланады. Енді
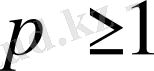 кез-келгеннақты сан болсын.
кез-келгеннақты сан болсын.
 жиынында
жиынында
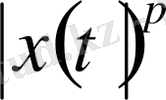 дәрежесі қосындыланатын
дәрежесі қосындыланатын
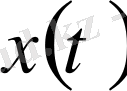 функцияларының жиыны да сызықтық кеңістік құрайтыны белгілі. Осы сызықты кеңістік
функцияларының жиыны да сызықтық кеңістік құрайтыны белгілі. Осы сызықты кеңістік
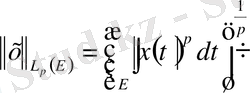 (1. 1. 14)
(1. 1. 14)
теңдігімен анықталатын норма енгізу арқылы
нормаланған сызықты кеңістікке
айналады. Бұл кеңістік әдетте
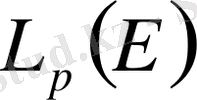 түрінде белгіленеді. Сонымен, әрбір
түрінде белгіленеді. Сонымен, әрбір
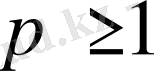 санына орай сызықтық кеңістік
санына орай сызықтық кеңістік
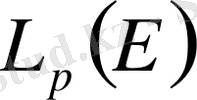 анықталды. Осы кеңістіктер Лебег кеңістіктері деп аталады.
анықталды. Осы кеңістіктер Лебег кеңістіктері деп аталады.
1. 1. 3 Шекті өлшемді кеңістіктегі норманың эквиваленттілігі
Анықтама 1. 1. 3
Айталық Е - сызықты кеңістік және Е кеңістігінде екі жағдаймен нормалар берілсін:
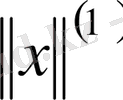 және
және
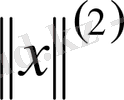 .
.
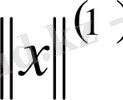 және
және
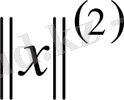 нормалары эквивалентті деп аталады, егер
нормалары эквивалентті деп аталады, егер
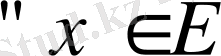 үшін
үшін
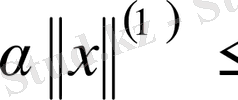
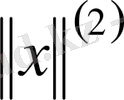

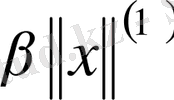 орындалатындай,
орындалатындай,
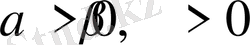 саны табылса.
саны табылса.
Норманың эквиваленттілік қатынасы келесі қасиеттерге ие:
- ~(рефлексифтілігі)
- егер~болса, онда~( симметриялылығы)
- егер~, ал~болса, онда~. (транзитивтілігі) .
Теорема 1. 1. 3 Барлық шекті өлшемді сызықты кеңістікте барлық нормалар эквивалентті.
Дәлелдеуі
.
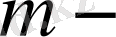 өлшемді Е сызықты кеңістікте
өлшемді Е сызықты кеңістікте
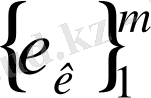 базисін белгілейміз, және
базисін белгілейміз, және
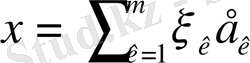 --
осы базис бойынша алынған
--
осы базис бойынша алынған
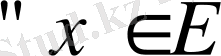 жіктелуі.
жіктелуі.
Айталық
 -
Е кеңістігіндегі тағы бір кез- келген норма болсын.
-
Е кеңістігіндегі тағы бір кез- келген норма болсын.
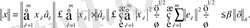
Ары қарай
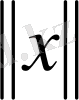 -
-
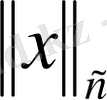 -
ға тәуелді,
-
ға тәуелді,
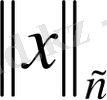 --
--
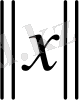 -
қа тәуелді болатынын көрсетейік. Бұл
-
қа тәуелді болатынын көрсетейік. Бұл
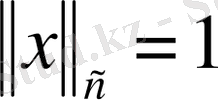 сферасында
сферасында
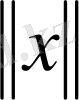 функциясын қарастырайық.
функциясын қарастырайық.
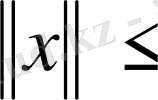
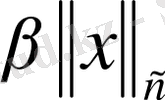 екенін ескеріп мынаны аламыз:
екенін ескеріп мынаны аламыз:
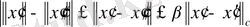 .
Бұдан
.
Бұдан
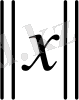 функциясының
функциясының
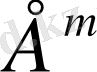 -дегі үзіліссіздігі шығады. Сонымен қатар
-дегі үзіліссіздігі шығады. Сонымен қатар
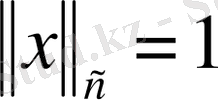 сферасында
сферасында
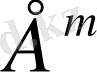 тұйық және шектелген жиын болады.
тұйық және шектелген жиын болады.
Лемма.
Егер
 болса, онда
болса, онда
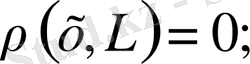 егер де
егер де
 болса, онда
болса, онда
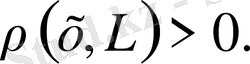
Дәлелдеуі.
Егер
 болса, онда
болса, онда
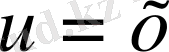 деп қабылдап,
деп қабылдап,
 аламыз. Яғни
аламыз. Яғни
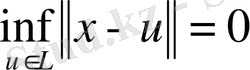 .
.
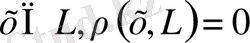 болсын. Онда
болсын. Онда
 анықтамасы бойынша кез келген натурал
анықтамасы бойынша кез келген натурал
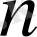 үшін
үшін
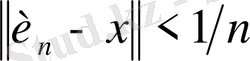 болғанда,
болғанда,
 табылады. Бұл жерде
табылады. Бұл жерде
 .
.
 тұйықталуының зерттелуінде
тұйықталуының зерттелуінде
 бірақ шарт бойынша
бірақ шарт бойынша
 . Алынған қарама- қайшылық
. Алынған қарама- қайшылық
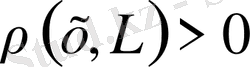 екенін дәлелдейді.
екенін дәлелдейді.
Егер
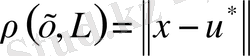 болғанда
болғанда
 элементі бар болса, онда
элементі бар болса, онда

 ішкі кеңістігінің
ішкі кеңістігінің
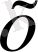 элементтері арқылы жақындаудың ең жақсы элементі деп аталады. Ең жақсы элемент жалғыз болмауы мүмкін, әрі мүлдем болмауы мүмкін.
элементтері арқылы жақындаудың ең жақсы элементі деп аталады. Ең жақсы элемент жалғыз болмауы мүмкін, әрі мүлдем болмауы мүмкін.
 шекті өлшемді болған жағдайда ол элемент бар болады. Шынында да,
шекті өлшемді болған жағдайда ол элемент бар болады. Шынында да,
 болса, онда
болса, онда
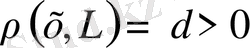 .
.
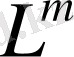 кеңістігінде
кеңістігінде
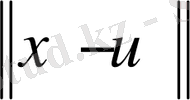 функциясын қарастырайық. Ол
функциясын қарастырайық. Ол
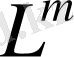 кеңістігінде үзіліссіз немесе кез келген
кеңістігінде үзіліссіз немесе кез келген
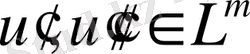 үшін төмендегі теңсіздік орындалады.
үшін төмендегі теңсіздік орындалады.
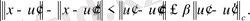
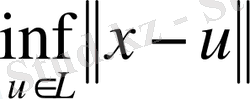 тек шарда орындалатынын көрсетейік.
тек шарда орындалатынын көрсетейік.
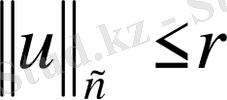 , мұндағы
, мұндағы
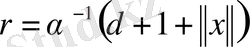 Демек, егер
Демек, егер
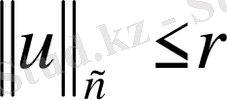 болса, онда
болса, онда

болады, яғни
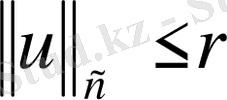 шарының сыртында
шарының сыртында
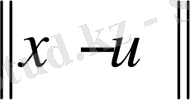 функциясының дәл төменгі шегін қабылдамайды.
функциясының дәл төменгі шегін қабылдамайды.
Теорема 1. 1. 3(а)
Айталық
 - нормаланған
- нормаланған
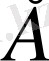 кеңістігінің шекті өлшемді ішкі кеңістігі болсын. Кез келген
кеңістігінің шекті өлшемді ішкі кеңістігі болсын. Кез келген
 үшін
үшін
 бар болады және
бар болады және
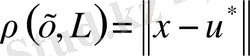 орындалады.
орындалады.
Мысал.
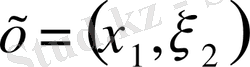 екі өлшемді қатарының
екі өлшемді қатарының
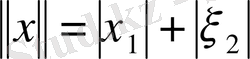 нормасымен берілген
нормасымен берілген
 -
кеңістігінен
-
кеңістігінен
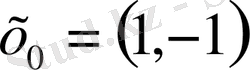 нүктесін және
нүктесін және
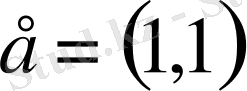 базистік векторымен, (
базистік векторымен, (
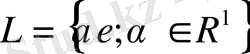 бір өлшемді
бір өлшемді
 ішкі кеңістігін аламыз. Ара қашықтығын анықтайық:
ішкі кеңістігін аламыз. Ара қашықтығын анықтайық:
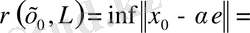
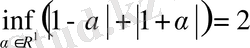 .
.
Зерттей келе,
 элементерінің көмегімен
элементерінің көмегімен
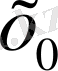 -ге жақындайтын
-ге жақындайтын
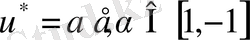 ең жақсы элементтерінің шексіз жиыны бар болатынына көзіміз жетеді. Келесі геометриялық тұжырымды келтірейік. Айталық үшөлшемді евклид кеңістігінде
ең жақсы элементтерінің шексіз жиыны бар болатынына көзіміз жетеді. Келесі геометриялық тұжырымды келтірейік. Айталық үшөлшемді евклид кеңістігінде
 жазықтығы берілсін. Ол
жазықтығы берілсін. Ол
 координата басынан өтеді, және
координата басынан өтеді, және
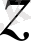 бірлік ұзындық векторы,
бірлік ұзындық векторы,
 перпендикуляр,
перпендикуляр,
 координата басымен берілген. Онда
координата басымен берілген. Онда
 -
ге тиісті кез келген
-
ге тиісті кез келген
 векторы үшін
векторы үшін
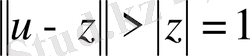 аламыз.
аламыз.
Рисс леммасы.
Айталық
 -нормаланған
-нормаланған
 кеңістігіндегі кеңістік,
кеңістігіндегі кеңістік,
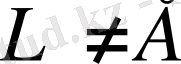 . Кез келген
. Кез келген
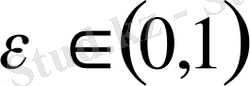 үшін
үшін
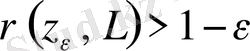 болатындай,
болатындай,
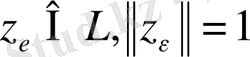 табылады.
табылады.
Дәлелдеуі.
Айталық
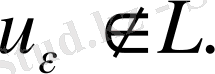
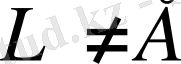 болғандықтан,
болғандықтан,
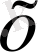 бар болады.
бар болады.
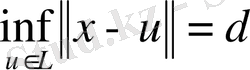 қоямыз,
қоямыз,
 анықтамасын қолданамыз. Кез келген
анықтамасын қолданамыз. Кез келген
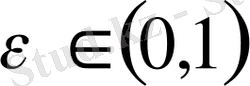 алып, және
алып, және
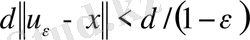 орындалатындай
орындалатындай
 табамыз. Енді
табамыз. Енді
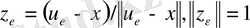 элементін қарастырайық.
элементін қарастырайық.
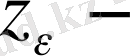 ізделінді элемент екенін ескерейік, шынында да,
ізделінді элемент екенін ескерейік, шынында да,
 .
.
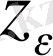 мен
мен
 арасындағы арақашықтық:
арасындағы арақашықтық:
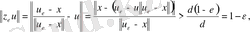 немесе
немесе
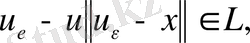 ал
ал
 үшін
үшін
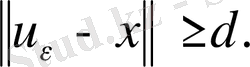
1. 2 МЕТРИКАЛЫҚ КЕҢІСТІКТЕР
1 . 2. 1 Метрикалық кеңістік ұғымы
 кез келген жиын болсын. Оның элементтерін
кез келген жиын болсын. Оның элементтерін
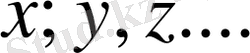 әріптерімен белгілейміз.
әріптерімен белгілейміз.
Екі айнымалылы, нақты сан мәнді
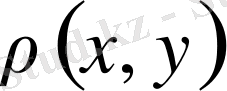 функциясы осы
функциясы осы
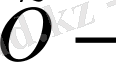 жиының элементтерінде анықталып және мына төмендегі шарттарды қанағаттандыратын болсын:
жиының элементтерінде анықталып және мына төмендегі шарттарды қанағаттандыратын болсын:
- ( симметриялық шарты)
- жәнетеңдігі тек қанаболғанда
орындалады. ( тепе-теңдік шарты) .
- Кез келгенэлементтері үшін:
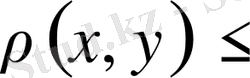
(1. 2. 1)
теңсіздігі орындалады. ( Бұл теңсіздік үшбұрыш теңсіздігі деп аталады. )
 жиынында анықталған, осы қасиеттерге ие
жиынында анықталған, осы қасиеттерге ие
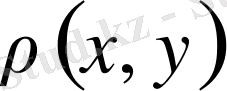 функциясы
арақашықтық
немесе
метрика
деп аталады.
функциясы
арақашықтық
немесе
метрика
деп аталады.
Анықтама 1. 2. 1
.
Метрика анықталған
 жиынын «метрикалық кеңістік» деп атайды.
жиынын «метрикалық кеңістік» деп атайды.
Метрикалық кеңістік
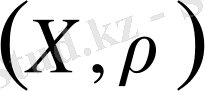 түрінде белгіленеді, бірақ көбінесе қысқаша, тек жиынның ған таңбасын көрсетіп,
түрінде белгіленеді, бірақ көбінесе қысқаша, тек жиынның ған таңбасын көрсетіп,
 арқылы белгілейміз.
арқылы белгілейміз.
Үшбұрыш теңсіздігінің салдары ретінде шығатын мына теңсіздіктерді атап көрсетейік. Метрикалық кеңістікте жатқан кез келген
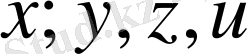 нүктелері үшін үшбұрыш теңсіздігін қайталай қолданып, мына теңсіздіктерді жазайық.
нүктелері үшін үшбұрыш теңсіздігін қайталай қолданып, мына теңсіздіктерді жазайық.
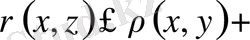
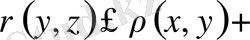
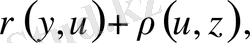
яғни,
Осыған ұқсас,
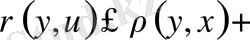
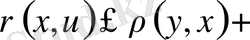
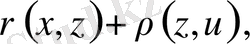
яғни,
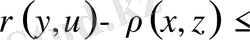
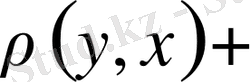
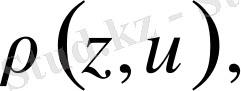
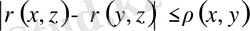
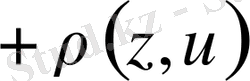 ,
,
Бұл әдетте
төртбұрыш теңсіздігі
деп аталады. Осы теңсіздіктен
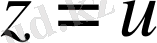 болған жағдайда
болған жағдайда
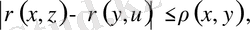
теңсіздігі шығады, ал бұл - екінші үшбұрыш теңсіздігі.
Тұжырым.
 кез келген нормаланған сызықтық кеңістік болсын.
кез келген нормаланған сызықтық кеңістік болсын.
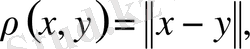 (1. 2. 2)
(1. 2. 2)
теңдігі осы кеңістікте метриканы анықтайды.
Дәлелдеуі
. Шарт бойынша
 нормаланған сызықтық кеңістік.
нормаланған сызықтық кеңістік.
Метриканың бірінші аксиомасы орындалатыны (1. 2. 2) теңдігінен айқын. Сондай-ақ,
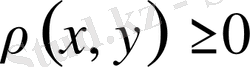 екендігі де норманың сәйкес қасиетінен шығады. Егер
екендігі де норманың сәйкес қасиетінен шығады. Егер
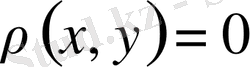 болса, онда
болса, онда
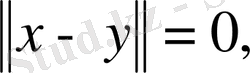 демек, норманың қасиеті бойынша,
демек, норманың қасиеті бойынша,
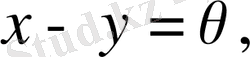 яғни
яғни
 .
.
Енді метриканың үшінші аксиомасын, яғни (1. 2. 1) теңсіздігін дәлелдейік. Кеңістіктің кез келген
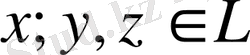 элементтерін алып, норманың үшінші аксиомасын пайдаланып, метрика үшін үшінші аксиоманың орындалатынын көреміз:
элементтерін алып, норманың үшінші аксиомасын пайдаланып, метрика үшін үшінші аксиоманың орындалатынын көреміз:
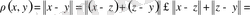
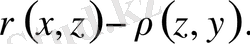 (1. 2. 3)
(1. 2. 3)
(1. 2. 1) теңдігінің норманы анықтайтыны, сонымен бірге
жиыны метрикалы жиын, яғни метрикалық кеңістік болғаны дәлелденді.
Теорема 1. 2. 1
Егер метикалық кеңістіктің нүктелерінен
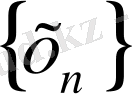 тізбегі
тізбегі
 нүктесіне жинақталса, онда
нүктесіне жинақталса, онда
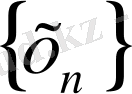 тізбектің кез келген
тізбектің кез келген
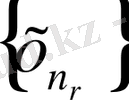 тізбекшесі де сол нүктеге жинақталады.
тізбекшесі де сол нүктеге жинақталады.
Дәлелдеуі.
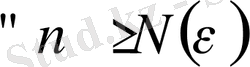 үшін
үшін
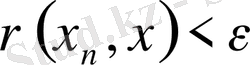 болса, онда
болса, онда
 үшін
үшін
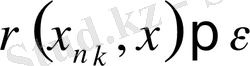 болады.
болады.
Теорема 1. 2. 1(а)
Метрикалық кеңістіктің нүктелерінің
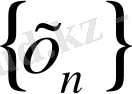 тізбегі жинақты болса, ол бір ғана шекке жинақталады.
тізбегі жинақты болса, ол бір ғана шекке жинақталады.
Дәлелдеуі.
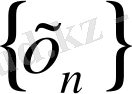 тізбек үшін
тізбек үшін
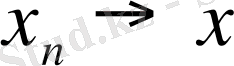 және
және
 деп жорылық. Онда
деп жорылық. Онда
 алғанда
алғанда
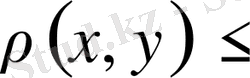
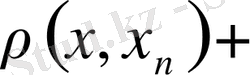
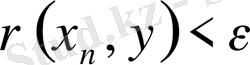
теңсіздігі жеткілікті үлкен
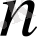 үшін орындалады.
үшін орындалады.
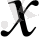 пен
пен
 белгілі нүктелер болғандықтан, ал
белгілі нүктелер болғандықтан, ал
 кез келген оң сан болғандықтан бұл теңсіздік
кез келген оң сан болғандықтан бұл теңсіздік
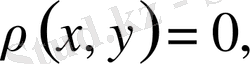 яғни
яғни
 болғанда ғана мүмкін.
болғанда ғана мүмкін.
Теорема 1. 2. 1(б)
Егер
 метрикалық кеңістіктің нүктелерінің
метрикалық кеңістіктің нүктелерінің
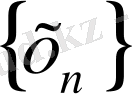 тізбегі
тізбегі
 нүктеге жинақталса, онда кез келген, белгіленіп алынған
нүктеге жинақталса, онда кез келген, белгіленіп алынған
 нүкте үшін
нүкте үшін
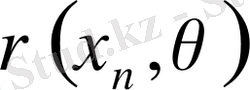 саны шектелген болады.
саны шектелген болады.
Дәлелдеуі. Үшбұрыш аксиомасы бойынша
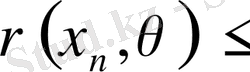
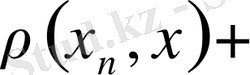
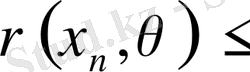
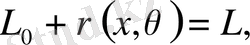
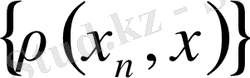 жинақталатын тізбек болғандықтан шектелген болады, демек
жинақталатын тізбек болғандықтан шектелген болады, демек
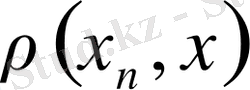 саны
саны
 тұрақты санынан аспайды.
тұрақты санынан аспайды.
1. 2. 2 Метрикалық кеңістіктің мысалдары
Метрика арқылы негізгі топологиялық ұғым - маңай анықталады. Соның негізінде басқа туынды ұғымдар беріледі. Кеңістік элементі ыңғайына қарай нүкте, немесе вектор деп атала беретінін еске сала кетейік.
 Элементтер үшін кез келген жиын
Элементтер үшін кез келген жиын
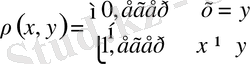
Белгіленген нүктелерді кеңістік деп алсақ, метрикалық кеңістік аламыз.
 Нақты сандар жиыны
Нақты сандар жиыны
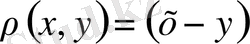 арақашықтықпен
арақашықтықпен
 метрикалық кеңістік пайда болады.
метрикалық кеңістік пайда болады.
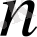 реттелген нақты сандар жиыны
реттелген нақты сандар жиыны
 қашықтығымен
қашықтығымен
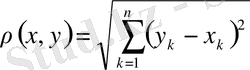
 өлшемді арифметикалық Евклид
өлшемді арифметикалық Евклид
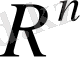 кеңістігі деп аталады.
кеңістігі деп аталады.
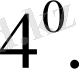
 ( n-өлшемді кеңістік) болсын.
( n-өлшемді кеңістік) болсын.
Егер
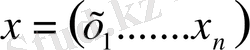 және
және
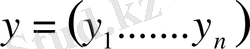 бұл кеңістіктің кез келген екі нүктесі болса, онда
бұл кеңістіктің кез келген екі нүктесі болса, онда
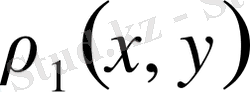 метрикасын мына өрнекпен
метрикасын мына өрнекпен

анықтауға болады, себебі
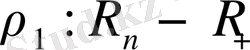 жоғарыдағы шарттарын қанағаттандырады. Олай болса,
жоғарыдағы шарттарын қанағаттандырады. Олай болса,
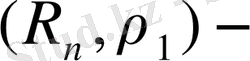 метрикалық кеңістік.
метрикалық кеңістік.
 Егер
Егер
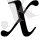 пен
пен
 нүктелері берілген болса, онда
нүктелері берілген болса, онда
 ара қашықтығын
ара қашықтығын
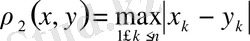
Өрнегі бойынша да анықтауға болады. Бұл өрнектің де 1) -3) шарттарын көз жеткізу қиын емес. Олай болса,
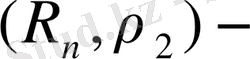 метрикалық кеңістік.
метрикалық кеңістік.

 жиыны
жиыны
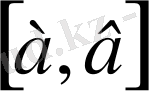 барлық үзіліссіз нақты функция үшін
барлық үзіліссіз нақты функция үшін
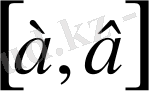 сегментінде
сегментінде
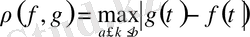
арақашықтығымен метрикалық кеңістік болады.
Анализде бұл кеңістік ерекше рөл ойнайды. Біз оны

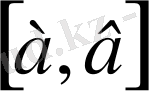 символымен белгілейміз.
символымен белгілейміз.

 орнына
орнына
 кеңістігін аламыз.
кеңістігін аламыз.
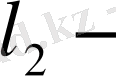 метрикалық кеңістік деп белгілеп,
метрикалық кеңістік деп белгілеп,
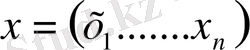 нүктелері нақты сан және шартты қанағаттандырса
нүктелері нақты сан және шартты қанағаттандырса
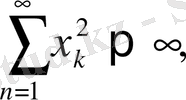
арақашықтығы келесі формуламен анықталады.
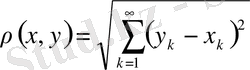
теңсіздік элементтерінен
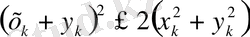 болса, онда
болса, онда
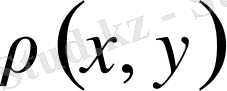 функциясы барлық
функциясы барлық
 үшін мағыналы,
үшін мағыналы,

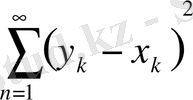 қатары тең, егер
қатары тең, егер
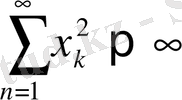 және
және
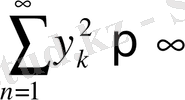 метрикалық кеңістік аксиомасын қанағаттандырады.
метрикалық кеңістік аксиомасын қанағаттандырады.
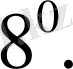 Функцияның барлық жиынтығы
Функцияның барлық жиынтығы
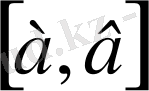 кесіндісінде үзіліссіз, бірақ арақашықтығы келесі түрде анықталады.
кесіндісінде үзіліссіз, бірақ арақашықтығы келесі түрде анықталады.
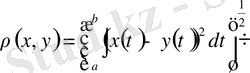
Мұндай метрикалық кеңістікті
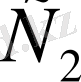
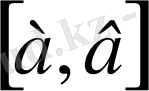 арқылы белгілеп және квадраттық метрикамен үзіліссіз функция кеңістігі деп аталады.
арқылы белгілеп және квадраттық метрикамен үзіліссіз функция кеңістігі деп аталады.
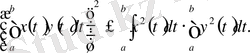
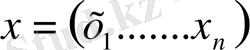 шектелген барлық нақты сандар жиынын қарастырамыз.
шектелген барлық нақты сандар жиынын қарастырамыз.
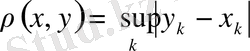
қойып метрикалық кеңістік аламыз.
1. 2. 3 Метрикалық кеңістікті толықтыру
Анықтама 1. 2. 3
Егер
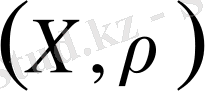 метрикалық кеңістігінде элементтердің
метрикалық кеңістігінде элементтердің
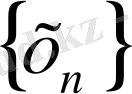 тізбегі үшін нөмірлер
тізбегі үшін нөмірлер
 кезде,
кезде,
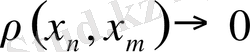 болса, онда бұл фундаменталь тізбек деп аталады.
болса, онда бұл фундаменталь тізбек деп аталады.
Анықтама 1. 2. 3(а)
Егер
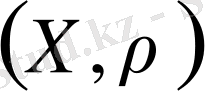 метрикалық кеңістігінде әрбір фундаменталь тізбек осы кеңістіктің элементіне жинақталатын болса, онда ол
толық кеңістік
деп аталады.
метрикалық кеңістігінде әрбір фундаменталь тізбек осы кеңістіктің элементіне жинақталатын болса, онда ол
толық кеңістік
деп аталады.
Анықтама 1. 2. 3(б)
Егер
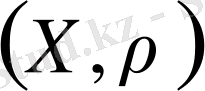 метрикалық кеңістігіндегі
метрикалық кеңістігіндегі
 жиынының әрбір
жиынының әрбір
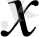 элементіне
элементіне
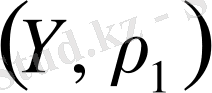 метрикалық кеңістігінің қайсібір
метрикалық кеңістігінің қайсібір
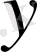 элементі сәйкес қойылған болса, онда
элементі сәйкес қойылған болса, онда
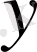 элементі
элементі
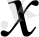 элементінің
бейнесі
деп аталады.
элементінің
бейнесі
деп аталады.
Анықтама 1. 2. 3(в) Егер
1)
 жиынында
жиынында
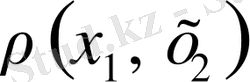 метрикасы анықталған,
метрикасы анықталған,
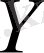 жиынында
жиынында
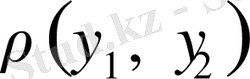 метрикасы анықталған болса;
метрикасы анықталған болса;
2)
 және
және
 жиындары изометриялы жиындар, яғни кез-келген
жиындары изометриялы жиындар, яғни кез-келген
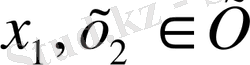 және олардың бейнелері
және олардың бейнелері
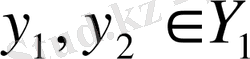 үшін
үшін
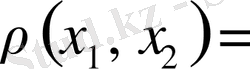
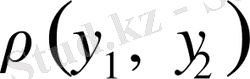 болса;
болса;
3)
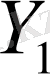 жиыны
жиыны
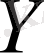 жиынында тығыз орналасқан болса, онда
жиынында тығыз орналасқан болса, онда
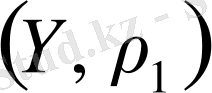 кеңістігі
кеңістігі
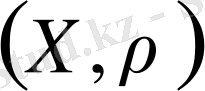 кеңістігінің толықтыруы деп аталады.
кеңістігінің толықтыруы деп аталады.
Теорема 1. 2. 3
Әрбір толық емес кеңістікті толықтыруға болады, яғни,
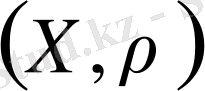 метрикалық кеңістігі толық емес болса, онда оның толықтыруы болатын
метрикалық кеңістігі толық емес болса, онда оның толықтыруы болатын
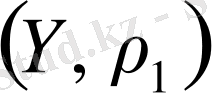 толық метрикалық кеңістігі әрқашанбар болады.
толық метрикалық кеңістігі әрқашанбар болады.
Теорема 1. 2. 3(Р. Бэр) Оңашан нүктесі жоқ толық метрикалық кеңістік еш жерде тығыз емес жиындардың саналымды бірігуі бола алмайды.
Дәлелдеуі.
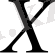 - толық метрикалық кеңістік болсын. Кері жору әдісін қолданып,
- толық метрикалық кеңістік болсын. Кері жору әдісін қолданып,
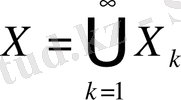 және мұндағы
және мұндағы
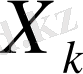 жиындарының әрқайсысы кеңістіктің еш жерінде тығыз емес деп жориық.
жиындарының әрқайсысы кеңістіктің еш жерінде тығыз емес деп жориық.
Енді радиусы 1-ге тең тұйық
 шарын алайық.
шарын алайық.
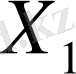 жиыны еш жерде тығыз емес, демек ол осы
жиыны еш жерде тығыз емес, демек ол осы
 шарында да тығыз емес. Сондықтан осы шардың ішінде
шарында да тығыз емес. Сондықтан осы шардың ішінде
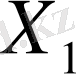 жиынының бір де нүктесі жоқ
жиынының бір де нүктесі жоқ
 тұйық шары табылады, яғни
тұйық шары табылады, яғни
 және
және
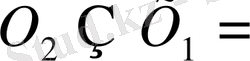 Ø.
Ø.
 шарының радиусын
шарының радиусын
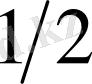 -ден аспайтын етіп алайық. Бұл
-ден аспайтын етіп алайық. Бұл
 шарында
шарында
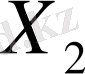 жиыны тығыз емес, сондықтан
жиыны тығыз емес, сондықтан
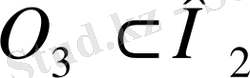 және
және
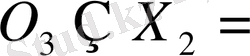 Ø болатындай
Ø болатындай
 тұйық шары табылады және оның радиусын
тұйық шары табылады және оның радиусын
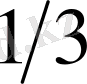 -ден аспайтындай етіп аламыз.
-ден аспайтындай етіп аламыз.
 шарында
шарында
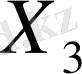 жиыны тығыз емес. Осы үрдісті шексіз жалғастыру нәтижесінде
жиыны тығыз емес. Осы үрдісті шексіз жалғастыру нәтижесінде
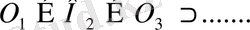 шарларының тізбегі пайда болады және олардың радиустары нөлге ұмтылады. Осы шарлардың бәріне де тиісті
шарларының тізбегі пайда болады және олардың радиустары нөлге ұмтылады. Осы шарлардың бәріне де тиісті
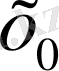 нүктесі бар, бірақ бұл нүкте
нүктесі бар, бірақ бұл нүкте
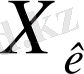 жиынының бір де нүктесі жоқ, демек
жиынының бір де нүктесі жоқ, демек
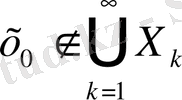 , яғни бұл бірігу кеңістіктің нүктелерін түгел қамти алмайды.
, яғни бұл бірігу кеңістіктің нүктелерін түгел қамти алмайды.
Кеңістік толық болғандықтан,
 , демек,
, демек,
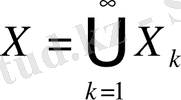 деген жоруымыз теріс болды. Теорема дәлелденді.
деген жоруымыз теріс болды. Теорема дәлелденді.
1. 3 СЫЗЫҚТЫ ОПЕРАТОРЛАР
1. 3. 1 Сызықты оператор ұғымы
Анықтама 1. 3. 1
Егер әрбір
 элементіне белгілі бір
элементіне белгілі бір
 элементі сәйкес қойылған болса, онда
элементі сәйкес қойылған болса, онда
 кеңістігінде оператор анықталған дейміз.
кеңістігінде оператор анықталған дейміз.
Операторлар теориясы -- операторлардың қасиеттерін, олардың әр түрлі есептерді шешуде қолданылуын зерттейтін функционалдық анализ бөлімі. Оператор ұғымы - математиканың жалпы ұғымдарының бірі. Мысалы, әрбір
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz