Көп айнымалы функциялардың интегралдық есептеулері: екі және үш еселі интегралдар мен қолданылуы


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
«Математика» кафедрасы
Курстық жұмыс
Тақырыбы: Көп аргументті функциялардың интегралдық есептеулері.
Орындаған: Абдулсаматқызы. А
Ғылыми жетекші:Назарова. К
Түркістан 2012
Мазмұны
Кіріспе . . . 3
I. тарау Екі еселі интегралдар . . . 5
1. 1. Екі еселі интегралдың анықтамасы . . . 5
1. 2. Екі еселі интегралдың қасиеттері . . . 7
1. 3. Екі еселі интегралдарда айнымалыларды ауыстыру . . . 10
1. 4. Екі еселі интегралды есептеу . . . 14
1. 5. Екі еселі интегралдың геометриядағы және физикадағы
кейбір қолданулары . . . 15
1. 6. Екі еселі интегралды полярлық координаталарда қарастыру . . . 17
1. 7. Екі еселі интегралдың механика есептерінде қолданулары . . . 21
II. тарау Үш еселі интегралдар . . . 23
2. 1. Үш еселі интегралдың анықтамасы . . . 23
2. 2. Үш еселі интегралдың қасиеттері . . . 24
2. 3. Үш еселі интегралды есептеу . . . 25
2. 4. Үш еселі интегралдың қолданулары . . . 26
2. 5. Кейбір механикалық және физикалық есептерге қолдану . . . 27
2. 6. Үш еселі интегралда айнымалыларды алмастыру . . . 29
Қорытынды . . . 31
Пайдаланылған әдебиеттер . . . 32
Кіріспе
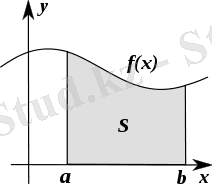
Интеграл(лат. іnteger - бүтін) -математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама. Осыған сай дифференциалдау формулалары мен ережелеріне сүйене отырып, интегралдаудың формулалары мен ережелерін алуға болады. Анықталған интеграл. y = f(x) теңдеуімен анықталған үздіксіз сызықтың доғасымен, Ox осінің AB кесіндісімен және AD, BC ординаталарымен қоршалған ABCD «қисық сызықты трапециясының» ауданын (S) табу керек болсын (суретті қ. ) . Ол үшін [a, b] кесіндісін a =x0<x1< . . . <xn-1<xn= b нүктелерімен n ұсақ аралықтарға бөліп (аралықтардың шамасы бір-біріне тең болуы шарт емес) және әрбір аралықтың ұзындығын Δx1, Δx2, . . . , Δxn арқылы белгілеп, сол аралықтардың әрқайсысына биіктігі f(ξ1), f(ξ2), . . . , f(ξn) -ке тең тік төртбұрыштар салайық, мұндағы ξk - [xk-1, xk] кесіндісіндегі кез келген нүкте (суретте k-аралыққа салынған тік төртбұрыш штрихталған және оның биіктігі f(ξk) -ке тең, мұндағы k =1, 2, . . . , n) . Сонда салынған тік төртбұрыштардың аудандарының қосындысын (Sn) қисық сызықты трапецияның (S) ауданымен шамалас деп қарастыруға болады:
S ≈ Sn= f(ξ1) Δx1+ f(ξ2) Δx2+ . . . + f(ξn) Δxn, немесе оны қосынды белгісін (Σ) пайдалана отырып, былайша жазуға болады:S ≈ Sn.
Бұл жерде [a, b] кесіндісі ұзындықтары неғұрлым кіші аралықтарға бөлінсе, Sn қосындысы ізделіп отырған ауданның шын мәніне (S-ке) солғұрлым жуық болып келеді. Демек S, бөлу нүктелерінің саны (n) шексіздікке, Δx-тың ең үлкен мәні нөлге ұмтылғанда, Sn қосындысының ұмтылатын белгілі шегі болады. Анықтама бойынша осы шек анықталған интеграл деп аталып: түрінде жазылады, мұндағы ∫ белгісі (латынның Summa сөзінің созылыңқы етіп жазылған бірінші әрпі) - интегралдың таңбасы; f(x) - интеграл астындағы функция; a және b сандары - интегралдың төменгі және жоғарғы шектері. Жалпы жағдайда, кез келген үздіксіз f(x) функциясының анықталған интегралы Sn қосындысының ұмтылатын шегі ретінде анықталады. Бірақ Sn-ді геометриялық фигураның ауданы деп түсіну шарт емес.
Егер a=b болса, онда анықтама бойынша: ; ал Жоғарғы шектің интегралдау функциясы ретінде қарастырылатын: анықталған интегралы (жоғарғы шегі айнымалы интеграл), интеграл астындағы f(x) функциясының бір алғашқы функциясы болады, яғни:бұдан интегралдық есептеудің негізгі теоремасы (Ньютон-Лейбниц формуласы) шығады: мұндағы F(x) - f(x) функциясының кез келген алғашқы функциясы. Бұл формула берілген анықталған интегралды есептеуге арналған негізгі амалдардың бірі. Анықталған интеграл арқылы жазық фигуралардың ауданы, қисық сызықтардың ұзындығы, дененің көлемі мен беті, ауырлық центрінің координаттары, инерция моменттері, берілген күштің атқаратын жұмысы, т. б. жаратылыстану мен техника есептері шешіледі.
Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. 9 - 15-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Тек 16 - 17-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. «Интегралдық есептеу» термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты. 19-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есептеуді дамытуға 19-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафнутий Чебышев үлкен үлес қосты. 19-ғасырдың аяғында және 20-ғасырдың басында жиын теориясының дамуы интегралдық есептеудің негізгі ұғымдарының тереңдеуіне және кеңеюіне себеп болды.
Анықталмаған интеграл
I. Тарау. Екі еселі интегралдар
1. 1. Екі еселі интегралдың анықтамасы.
Екі аргументті
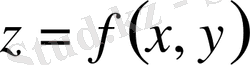 функциясының анықталу облысы
функциясының анықталу облысы
 де контур
де контур
 мен шектелсін делік. Контур
мен шектелсін делік. Контур
 графиктері
графиктері
 не
не
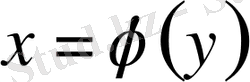 түріндегі бөліктерден тұрсын делік. Мұндай контурлар қарапайым контур делінеді. Облыс
түріндегі бөліктерден тұрсын делік. Мұндай контурлар қарапайым контур делінеді. Облыс
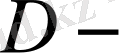 ны қалауымызша
ны қалауымызша
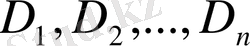 түріндегі сәйкес аудандары
түріндегі сәйкес аудандары
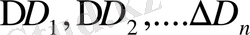 болатын
болатын
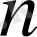 бөлікке жіктейміз. Әрбір
бөлікке жіктейміз. Әрбір
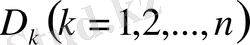 облысындағы нүктелердің арақашықтықтарының ең үлкенін
облысындағы нүктелердің арақашықтықтарының ең үлкенін
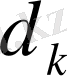 деп белгілеп, диаметр деп атаймыз. Жекелеген облыс
деп белгілеп, диаметр деп атаймыз. Жекелеген облыс
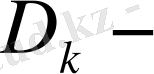 да қалауымызша бір
да қалауымызша бір
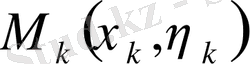 нүктесін алып, функцияның мәнін
нүктесін алып, функцияның мәнін
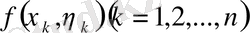 есептейміз. Мынадай қосындыны
есептейміз. Мынадай қосындыны
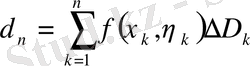 (1. 1. 1)
(1. 1. 1)
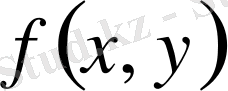 функциясы үшін
функциясы үшін
 облысы бойынша екі өлшемді интегралдық қосынды дейміз.
облысы бойынша екі өлшемді интегралдық қосынды дейміз.
Анықтама.
Егер
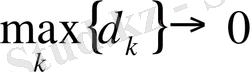 (1. 1. 1) интегралдық қосындының шегі бар болып, ал шек
(1. 1. 1) интегралдық қосындының шегі бар болып, ал шек
 облысын майда
облысын майда
 бөліктеріне жіктеу тәсілімен де, олардың әрқайсысында
бөліктеріне жіктеу тәсілімен де, олардың әрқайсысында
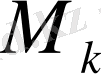 нүктесін таңдау тәсіліненде тәуелді болмаса, ол шектік мән
нүктесін таңдау тәсіліненде тәуелді болмаса, ол шектік мән
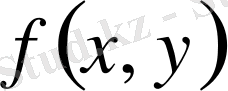 функциясының
функциясының
 облысы бойынша екі еселі интегралы деп аталады да, былай белгіленеді:
облысы бойынша екі еселі интегралы деп аталады да, былай белгіленеді:
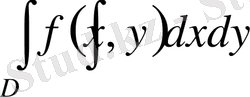 (1. 1. 2)
(1. 1. 2)
Егерде (1. 1. 2) интегралы бар болса, функция
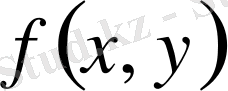 облыс
облыс
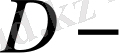 да интегалданатын функция дейміз. Қосынды (1. 1. 1) -ден байқалып тұрғандай функция
да интегалданатын функция дейміз. Қосынды (1. 1. 1) -ден байқалып тұрғандай функция
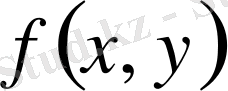 облыс
облыс
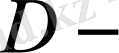 да шектелген болуы интеграл (1. 1. 2) бар болуы үшін шарт.
да шектелген болуы интеграл (1. 1. 2) бар болуы үшін шарт.
Енді интегралдық қосынды (1. 1. 1) мен интеграл (1. 1. 2) -нің тәжірибеде кездесетін кейбір мысалдарына тоқталайық:
Қисық сызықты цилиндр деп төменгі табаны
 жазықтығындағы
жазықтығындағы
 фигурасы болатын, ал жоғарыдан
фигурасы болатын, ал жоғарыдан
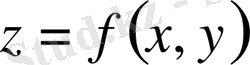 бетімен, ал бүйірден-цилиндрлік бетпен шектелген
бетімен, ал бүйірден-цилиндрлік бетпен шектелген
 денесін түсінеміз. Осы дененің көлемін табу талап етілсін.
денесін түсінеміз. Осы дененің көлемін табу талап етілсін.
Ол үшін қисық сызықты
 цилиндрдің табаны
цилиндрдің табаны
 -ны қисықтардың жәрдемімен
-ны қисықтардың жәрдемімен
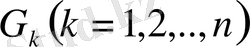 бөліктерге жіктесек,
бөліктерге жіктесек,
 денесі табандары
денесі табандары
 болатын
болатын
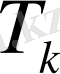 цилиндрлеріне жіктеледі. Сөйтіп
цилиндрлеріне жіктеледі. Сөйтіп
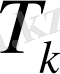 цилиндрлерінің көлемдерінің қосындысы цилиндр
цилиндрлерінің көлемдерінің қосындысы цилиндр
 нің көлемін береді.
нің көлемін береді.
Цилиндр
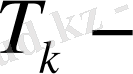 нің көлемін табу үшін әрбір бөлек
нің көлемін табу үшін әрбір бөлек
 деп қалауымызша нүкте
деп қалауымызша нүкте
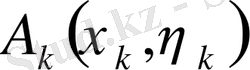 алып, л бөліктің ауданын
алып, л бөліктің ауданын
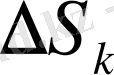 деп белгілеп, мынадай көбейтінді түземіз
деп белгілеп, мынадай көбейтінді түземіз
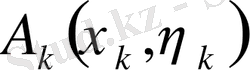
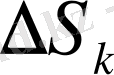 , демек
, демек
 денесінің көлемінің жуық мәні үшін
денесінің көлемінің жуық мәні үшін
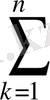
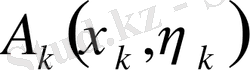
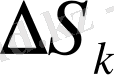 (1. 1. 3)
(1. 1. 3)
қосындысын алуға болады. Егер (1. 1. 3) қосындысында бөліктердің өлшемдері шексіз кішірейген жағдайда шекке көшсек, сол шек іздеп отырған қисық сызықты цилиндр
 нің көлемін береді. Екі еселі интеграл (1. 1. 2) -нің анықтамасына сай қисық сызықты цилиндрдің көлемі екі еселі интегралмен анықталатыны белгілі болды. Осында
нің көлемін береді. Екі еселі интеграл (1. 1. 2) -нің анықтамасына сай қисық сызықты цилиндрдің көлемі екі еселі интегралмен анықталатыны белгілі болды. Осында
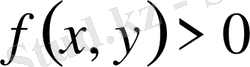 екенін ескеруіміз керек.
екенін ескеруіміз керек.
Тәжірибе (1. 1. 1), не (1. 1. 3) секілді қосындылардың шегін ескерту керектігі әртүрлі есептерде кездеседі.
Мысалы, жазық фигураның массасын есептеу, статикалық моменнттер мен жазық фигураның ауырлық центрін анықтау мәселесінде кездеседі.
1. 2. Екі еселі интегралдардың қасиеттері.
Екі еселі интегралдың жоғарыда берілген анықтамасынан туындайтын кейбір қарапайым қасиеттерін келтіреміз:
1-қасиет
. Егер
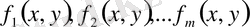 функцияларының әрқайсысы
функцияларының әрқайсысы
 облысында интегралданса, олардың алгебралық қосындысы да сол облыста интегралданып
облысында интегралданса, олардың алгебралық қосындысы да сол облыста интегралданып
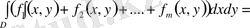 (1. 2. 1)
(1. 2. 1)
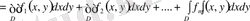
болады.
Дәлелдеу. Интегралдық қсынды құрастырып,
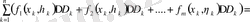
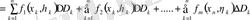
екенін ескеріп, екі еселі интеграл анықтамасына сай шекке көшсек, әрбір
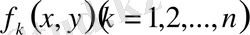 функциясы
функциясы
 облысында интегралданатын болғандықтан қасиеттің шындығына көзіміз жетеді.
облысында интегралданатын болғандықтан қасиеттің шындығына көзіміз жетеді.
2-қасиет
. Егерде
 облысында
облысында
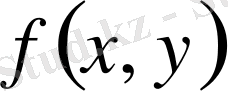 функциясы интегралданса, кез-келген тұрақты
функциясы интегралданса, кез-келген тұрақты
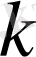 үшін
үшін
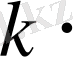
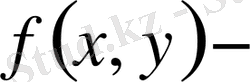 те интегралданады және
те интегралданады және
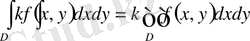
Бұл теңдіктің растығы екі еселі интеграл анықтамасынан туындайды.
Екі еселі интегралдың осы екі қасиеті интегралдың сызықтық қасиеті аталады.
3-қасиет
. Егер
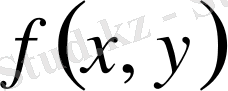 функциясы
функциясы
 де интегралданып және таңбасын өзгертпесе, оның екі еселі интегралы да сол
де интегралданып және таңбасын өзгертпесе, оның екі еселі интегралы да сол
 блысы бойынша тұрақты таңбасын сақтайды.
блысы бойынша тұрақты таңбасын сақтайды.
Дәлелдеу.
Егер
 облысында
облысында
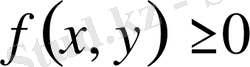 болса, интегралды қосындыда оң таңбасын сақтап, шекке көшкенде ол таңба өзгермейді. Сол секілді функция таңбасы теріс болса да екі еселі интегралды тұрақты таңба сақтайды.
болса, интегралды қосындыда оң таңбасын сақтап, шекке көшкенде ол таңба өзгермейді. Сол секілді функция таңбасы теріс болса да екі еселі интегралды тұрақты таңба сақтайды.
4-қасиет.
Егер
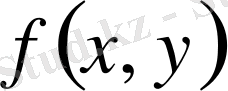 пен
пен
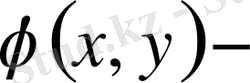 функциялары
функциялары
 облысында интегралданып,
облысында интегралданып,
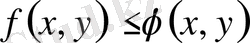 теңсіздігі орындалса,
теңсіздігі орындалса,
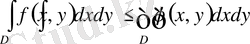
болады.
Дәлелдеу.
Егер
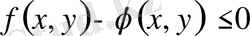 деп жазып, 3-қасиетті пайдаланып
деп жазып, 3-қасиетті пайдаланып
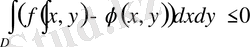
деп жазамыз. Енді екі еселі интегралдың 1-қасиетін пайдалансақ, керек қасиетіміз дәлелденеді.
5-қасиет.
Егер
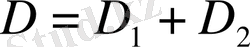 облысында
облысында
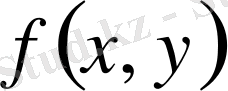 функциясы интегралданса,
функциясы интегралданса,
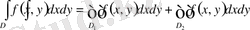
болады.
Дәлелдеу. Біз интегралдық қосынды үшін
 облысын
облысын
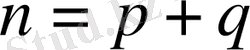 бөліктерге бөліп, әр бөліктің диаметрі нольге ұмтылатындай шекке көшкенімізде
бөліктерге бөліп, әр бөліктің диаметрі нольге ұмтылатындай шекке көшкенімізде
 және
және
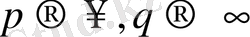 болар еді. Сөйтіп
болар еді. Сөйтіп
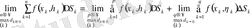
(
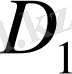 де
де
 бөлік,
бөлік,
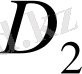 де
де
 бөлік) . Теңдігінен 5-қасиетті болар еді. Бұл қасиетті екі еселі интегралдың аддавтигі деп атайды.
бөлік) . Теңдігінен 5-қасиетті болар еді. Бұл қасиетті екі еселі интегралдың аддавтигі деп атайды.
6-қасиет. Ауданы 3-ке тең
 облысында интегралданатын
облысында интегралданатын
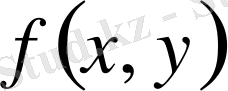 функциясы мына теңсіздікті
функциясы мына теңсіздікті
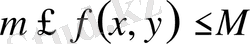 қанағаттандырса,
қанағаттандырса,
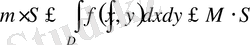 болады.
болады.
Дәлелдеу. Берілген
 облысын қарапайым
облысын қарапайым
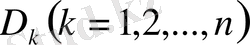 бөліктерге бөліп, нүкте
бөліктерге бөліп, нүкте
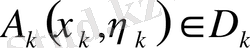 алып,
алып,
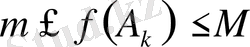 болатынын көреміз. Енді
болатынын көреміз. Енді
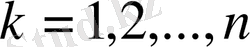 деп жинақтасақ,
деп жинақтасақ,
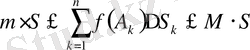 болар еді. Осыдан шекке көшсек 6-қасиет дәлелденеді. Біз 6-қасиеттен
болар еді. Осыдан шекке көшсек 6-қасиет дәлелденеді. Біз 6-қасиеттен
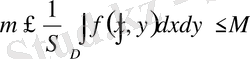
деп алып
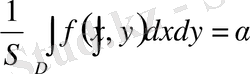
десек,
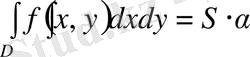
болар еді. Егер
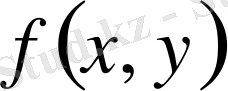 функциясы
функциясы
 облысында үзіліссіз болса, онда оның сол облыста ең кіші мәні
облысында үзіліссіз болса, онда оның сол облыста ең кіші мәні
 және ең үлкен мәні
және ең үлкен мәні
 болып, функция сол аралықтағы мәндердің бәрін қабылдауы тиіс, сондықтан
болып, функция сол аралықтағы мәндердің бәрін қабылдауы тиіс, сондықтан
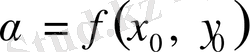 болатын
болатын
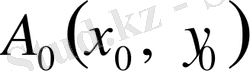 нүктесі
нүктесі
 облысында жатады. Сөйтіп,
облысында жатады. Сөйтіп,
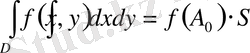
болады. Екі еселі интегралдың осы жазылу түрі өте жиі қолданылады.
1. 3. Екі еселі интегралда айнымалыларды алмастыру.
Бізге екі еселі интеграл
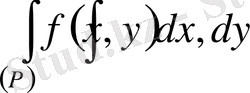 берілсін және
берілсін және
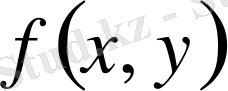 функциясы шенелген жабық P облысында үзіліссіз болсын. Мына формулалар
функциясы шенелген жабық P облысында үзіліссіз болсын. Мына формулалар
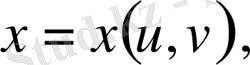
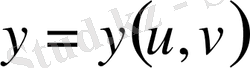
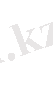 (1. 3. 1)
(1. 3. 1)
Арқылы біз жаңа
 және
және
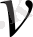 аргументтерге көшеміз. Керісінше
аргументтерге көшеміз. Керісінше
 және
және
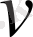 (7) формуладан
(7) формуладан
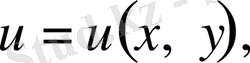
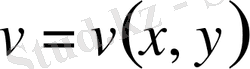 (1. 3. 2)
(1. 3. 2)
формулаларымен анықталады деп санайық. (7) формулалар арқылы Р облысындағы
 нүктесіне
нүктесіне
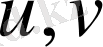 координаттар жазықтығында
координаттар жазықтығында
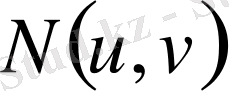 нүктесі сәйкес болады. Осындай
нүктесі сәйкес болады. Осындай
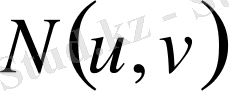 нүктелердің жиынын
нүктелердің жиынын
 деп белгілейік. Егер
деп белгілейік. Егер
 облысында (7) формуладағы функциялардың дербес туындылары бар болып мына анықтауыш
облысында (7) формуладағы функциялардың дербес туындылары бар болып мына анықтауыш
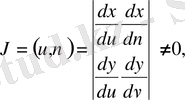
онда
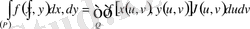
 (1. 3. 3)
(1. 3. 3)
Бұл жерде
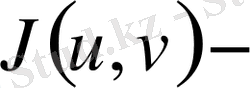 ны
ны
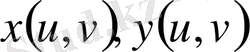 функциялардың якобианы деп атайды. (9) формуланың дәлелдеуі өте күрделі, сондықтан оны келтірмейміз.
функциялардың якобианы деп атайды. (9) формуланың дәлелдеуі өте күрделі, сондықтан оны келтірмейміз.
Егер (7) формулада полярлық координаталарға көшетін болсақ, яғни
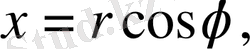
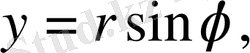
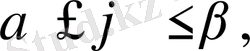
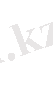
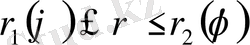 онда
онда
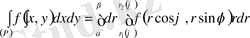
болады.
Мысалы.
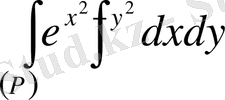 есептеу керек.
есептеу керек.
P - бірінші квадратта жататын
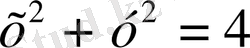 дөңгелектің төрттен бірі болсын.
дөңгелектің төрттен бірі болсын.
Шешуі.
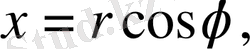
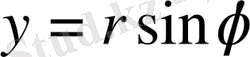 формулаларын пайдаланып
формулаларын пайдаланып
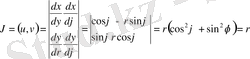
P облысында r айнымалысы 0 ден 2-ге дейін, ал
 ден
ден
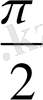 дейін өзгереді. Сондықтан
дейін өзгереді. Сондықтан
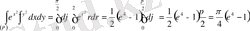
1. 4. Екі еселі интегралды есептеу.
Екі еселі интегралды есептеу оны қайталама интегралға келтіру арқылы орындалады, сондықтан сол қайталама интеграл ұғымына тоқталып өтелік. Егерде тіктөртбұрыш
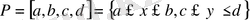
де анықталған функция
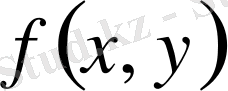 үшін интеграл
үшін интеграл
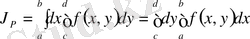 (1. 4. 1)
(1. 4. 1)
бар болса, онда мұны қайталама интеграл дейді. Осындағы ішкі интеграл есептелгенде интеграл есептелмейтін айнымалы тұрақты сан рөлінде болады.
Қисық сызықты облыстар үшін қайталама интеграл ұғымын кіргізер алдында мына анықтаманы берейік:
Анықтама.
Егерде жабық
 облысының ішкі нүктесінен өтетін кез келген түзу координаталар системасының бір осіне параллель болып және сол облыстың тек екі шекаралық нүктелері арқылы ғана қиылысса, онда сол
облысының ішкі нүктесінен өтетін кез келген түзу координаталар системасының бір осіне параллель болып және сол облыстың тек екі шекаралық нүктелері арқылы ғана қиылысса, онда сол
 облысын сол ось бағытында дұрыс облыс дейді. Ал облыс
облысын сол ось бағытында дұрыс облыс дейді. Ал облыс
 барлық координаталар осьтері бағытында дұрыс облыс болса, онда ол облысты дұрыс облыс дейді.
барлық координаталар осьтері бағытында дұрыс облыс болса, онда ол облысты дұрыс облыс дейді.
Егерде
 облысы бізге былайша берілсе
облысы бізге былайша берілсе
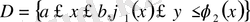
немесе
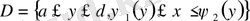
болса. Біз мына интегралды (
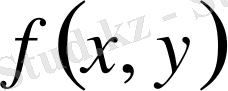
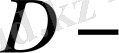 да анықталған)
да анықталған)
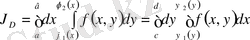 (1. 4. 2)
(1. 4. 2)
Қайталама интегралдар
 бойынша дейміз. (1. 4. 1) теңдігімен анықталған қайталама интегралдар (1. 4. 2) түріндегі қайталама интегралдың
бойынша дейміз. (1. 4. 1) теңдігімен анықталған қайталама интегралдар (1. 4. 2) түріндегі қайталама интегралдың
 облысы тіктөртбұрыш болатын жекелеген түріне жатады. Біз екі еселі интегралды есептеуді
облысы тіктөртбұрыш болатын жекелеген түріне жатады. Біз екі еселі интегралды есептеуді
 облысы қисық сызықты болып келген жағдайын қарастырамыз.
облысы қисық сызықты болып келген жағдайын қарастырамыз.
Бізге екі еселі интеграл
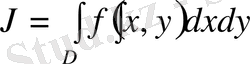 (1. 4. 3)
(1. 4. 3)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz