Ақырлы элементтер әдісі: негіздері, интерполяциялық полиномдар және вариациялық тұжырымдама


Кіріспе
Ақырлы элементтер әдісі, физикада және техникада кездесетін дифференциалдық теңдеулерді шешудің сандық әдісі болып табылады. Бұл
әдістің пайда болу космостық зерттеулерге байланысты (1950ж) . Алғашқы рет ол Тернердің, Клуждың, Мортин және Топптың [1] жұмыстарында жарық көрді. Бұл жұмыс басқа жұмыстардың пайда болуына түрткі болды: Мысалы: құрылыс механикасының және тұтас механикасының есептерін ақырлы элементтер әдісінің қолданылуымен бірнеше мақалалар жарыққа шықты. 1963 жылы Мелош [2] жасаған әдістің теориялық құрылымы маңызды болды. Құрылыс механикасында потенциалдың энергияны минимизациялау арқылы ақырлы элеметтер әдісі мен есепті сызықтың теңдеулер жүйесіне келтіруге болатынын көрсетеді.
Ақырлы элементтер әдісіні минимизациялау процедурасымен байланысы техниканың басқада облыстарындағы есептері шешкенде оны кең қолдануға болатынына көрсетеді. Әдіс, Лаплас немесе Пуассон теңдеулерімен сипатталатын есептерді шешуге қолданылады. Алғашқы публикацияларда [3. 4] ақырлы элементтер әдісінің көмегімен жылудың таралу есебі шешілген болатын. Сосын әдісті гидромеханика есептерін шешкенде, атап айтқанда ортадағы сұйықтың ағысы есебін шешкенде қолданылған.
Ақырлы элементтер әдісін қолдану облысы біршама кеңейді. Мысалы: құрылыс механикасының, жылу таралудың, гидромеханиканың есептеріндегі элементтерді анықтайтын теңдеулер, Галеркин әдісі немесе ең кіші квадраттар тәсілі сияқты әдістердің көмегімен оңай алынатыны көрсетілген [5. 6] . Осы фактіның қойылыуы ақырлы элементтер әдісінің теореиялық негіздеуде маңызды роль атқарды, себебі оны кез келген дифференциалдық теңдеулерді шешкенде қолдануға болады.
Құрылыс механиканың есептерін шешуде ақырлы элементтер әдісі дифференциалдық теңдеулерді шешуде немесе дифференциалдық теңдеулер жүйесін шешудің жалпы сандық әдісіне айналды. Есептеу машинасы көптеген қиын сандық есептердің орындалуын тездеткен болатын. Космыстық кеңістікті зерттеу кезінде фундаментальды зерттеулерді жүргізу көп қаражатты керек етті және универсалды есептеу программаларын жүзеге асыру көзделді. Ақырлы элементтер әдісі ұшақты, ракетаны т. б. проектілегенде қолданылады.
Қарапайым бір өлшемді есеп мазмұндауға тиімді, себебі тек солғана тиянақты санды мысал үшін барлық есептеулерді түсіндіріп береді. Екі өлшемді жағдайда, тіпті үшөлшемді жағдайда есептеу көлемі бұл үшін өте үлкен. Төменде келтірілетін талқылаулар бөлектенген элементтерге қатысты болғандықтан барлық шамалар белгілеулеріндегі жоғарғы индекстері
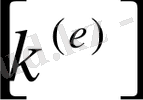 және
және

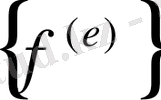 -лерді қоспағанда, түсіп қалып отырады.
-лерді қоспағанда, түсіп қалып отырады.
Ақырлы элементтер әдісі элемент деп аталатын ішкі облыстың ақырлы санында анықталған бөлікті -үзіліссіз функциялардың жиынында құрылатын дискретті модельдің үзіліссіз функциясының аппроксимациясының идеясына негізделген. Элемент функциясы ретінде көбінесе полином қолданылады. Полиномның реті үзіліссіз функция, әрбір элемент түйінде қолданылатын сандарға байланысты.
I Тарау. Ақырлы элементтер әдісі
§ 1. 1 Ақырлы элементтер әдісінің негізгі
концепциясы.
Ақырлы элементтер әдісінің негізгі идеясы, кез келген үзіліссіз шаманы, температура, қысым және орын ауыстыру сияқты шамаларды, дискретті модельге аппроксимациялаудан тұрады; яғни олар ішкі областың ақырлы санында анықталған бөлікті үзіліссіз функциялар жиынында құрылған болуы керек. Бөлікті-үзіліссіз функциялар қарастырып отырған облыстың нүктелерінің ақырлы санындағы үзіліссіз шамалардың көмегімен анықталады.
Жалпы жағдайда үзіліссіз шама алдын-ала белгісіз және осы шаманың мәнін облыстың қандай да бір ішкі нүктесінде анықтау керек . Бірақ, дискретті модельді, алдымен егер облыстың әрбір ішкі нүктесінде осы шаманың сандық мәні белгілі деп ұйғарсақ, онда оны оңай құрастыруға болады. Бұдан үзіліссіз шаманың дискретті моделін жасау келесі түрде жүзеге асады:
1. Қарастырылып отырған облыста нүктелердің ақырлы саны белгіленіп алынады. Бұл нүктелер түйін нүктелері немесе жай түйін деп аталады.
2. Анықталу керек әрбір түйін нүктелеріндегі үзіліссіз шаманың мәні айнымалы деп есептеледі.
3. Үзіліссіз шаманың анықталу облысы элемент деп аталатын ішкі облыстардың ақырлы санына бөлінеді, Бұл элементтердің жалпы түйін нүктелері болады және жиынытығында облыс формасын аппроксимациялайды.
4. Үзіліссіз шама әрбір элементте, осы шаманың түйіндік мәнінің көмегімен анықталатын полином ретінде аппроксимацияланады. Әрбір элемент үшін өз полиномы анықталады, бірақ полиномдар элементтің шекарасының бойында шаманың үзіліссіздігі сақталатындай етіліп таңдалады.
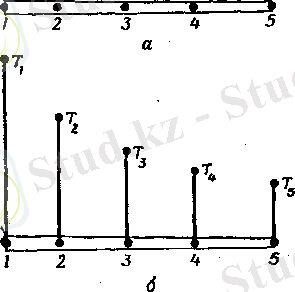
1. 1-сурет. 1. 2сурет.
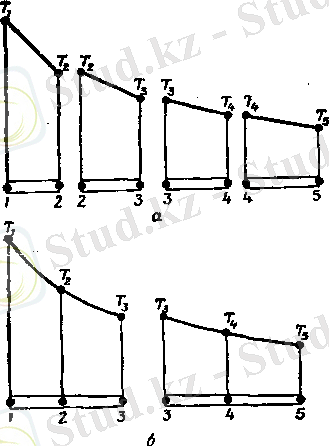
Ақырлы элементтер әдісінің негізгі концепциясы 1. 1-суретте көрсетілгендей, стерженьдегі температураның таралуы берілген бір өлшемді мысалда көрнекі түрде көрсетілген. Анықталу облысы х өсінің бойындағы OL кесіндісі болатын, Т(x) үзіліссіз шамасы қарастырылады. х өсінде бес нүкте белгіленіп және нөмірленеді (1. 2 a сур. ) . Бұл түйін нүктелері; оларды бір-бірінен бірдей ара қашықтықта орналастыру міндетті емес. Қарастыруға бес нүктеден де көп алуға болады, бірақ әдістің басты идеясын түсіндіру үшін осы бес нүкте толық жеткілікті. Берілген жағдайда Т(x) мәні әрбір түйін нүкте лерінде белгілі. бұл белгіленген мәндер графиктік түрде 1. 2б суретте көрсетілген және нөмірленген түйін нүктелері сәйкесінше
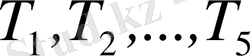
 болып белгіленген
болып белгіленген
 1. 3-сурет. 1. 4-сурет.
1. 3-сурет. 1. 4-сурет.
Облысты элементтерге бөлу екі түрлі тәсілмен жүргізілуі мүмкін. Мысалы, әрбір элементті екі көрші түйін нүктелерімен шектеген, төрт элемент бейнелеуге болады. (1. 3а) немесе облысты әрбіреуінде үш түйінен болатындай етіп екі элементке бөлуге болады (1. 3б) . Элементке сәйкес келетін полином элементтің түйін нүктелеріндегі Т(x) мәні бойынша анықталады. Әрбір элементке екі түйін болатындай етіп, облысты төрт элементке бөлген жағдайда, элемент функциясы х бойынша сызықты болады. (екі нүкте түзу сызықты бірмәнді анықтайды ) . Соңғы Т(x) аппроксимациясы төрт бөлікті сызықты функциялардан тұрады, олардың әрбіреуі бөлек элементте анықталған (1. 4а-сур. ) .
Үш түйін нүктелі екі элементке облысты бөлудің келесі тәсілі элементтің функциясы екінші дәрежелі полином түрінде көрсетуге келтіріледі. Бұл жағдайда соңғы Т(x) аппроксимациясы екі бөлік үзіліссіз квадрат функциясының жиынтығы болады. Бұл жуықтау бөлік үзіліссіз болатынын ескереміз, себебі бұл екі функцияның графигинің көлбеулік бұрышы үшінші түйінде әртүрлі мәнде болуы мүмкін.
Жалпы жағдайда температураның таралуы белгісіз және біз қандай да бір нүктедегі осы шаманың мәнін анықтағымыз келеді. Дискретті модельді құрастырудың методикасы жоғарыда сипатталғандай болады. бірақ бір қосымша қадам қосылғаннан болады. Түйіндер жиыны және осы түйіндердегі
 температуралардың мәндері яғни олар алдын ала белгісіз болғандықтан екі айнымалы болып тұр.
температуралардың мәндері яғни олар алдын ала белгісіз болғандықтан екі айнымалы болып тұр.
Облыс элементтерге бөлінеді, яғни олардың әрқайсысында сәйкес элемент функциясы анықталады. Т(х) түйін мәндері енді, шын температура үлестірілуіне «ең жақсы» жуықтау жүзеге асуы үшін, осындай етіп «реттелген» болуы керек . Бұл реттеу есепті физикалық байланысқан қандайда бір шаманы минимизациялау жолымен жүзеге асады. Егер жылу таралу есебі қарастырылып жатса, онда сәйкесінше дифференциал теңдеулермен байланысқан функционал минимизацияланады. Минимизация процесі Т(х) түйін мәніне қатысты сызықты алгебралық теңдеулер жүйесін шешуге келтіріледі.
1. 5-сурет

1. 6-сурет.
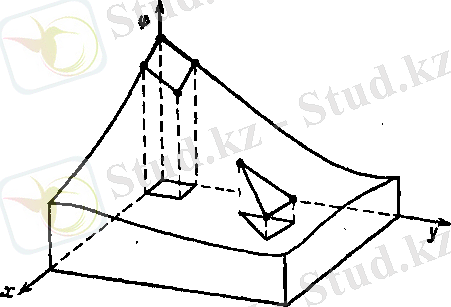
Екі үш өлшемді облыста анықталған үзіліссіз шаманың дискретті моделін құрастырған кездегі ақырлы элементтер әдісінің негізгі концепциясы осы сияқты қолданылады. Екі өлшемді жағдайында элементтер х, у-тің функциялары болып сипатталады. Сонымен қатар көбінесе элементтер үшбұрыш немесе төртбұрыш формасында қарастырылады. Енді элементтер функциясы жазық (1. 5-сурет) немесе қисықсызықты (1. 6-сурет) беттермен бейнеленеді. Элемент функциясы жазықтық болып көрінеді, егер берілген элемент үшін түйін нүктелердің минимал саны алынады яғни үшбұрышты элемент үшін үш нүкте, ал төртбұрыш элемент үшін төртк нүкте.
Егер қолданылатын түйін саны минималдан көп болса, онда элемент функциясына қисықсызықты бетке сәйкес келеді. Сонымен қатар, түйін санының артықтығы шекаралары қисықсызықты элементті қарастыруға алып келеді. Екі өлшемді үзіліссіз шаманың
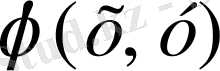 соңғы аппроксимациясы бөлік-үзіліссіз беттердің жиынтығы ретіде болады, яғни олардың әрбіреуі түйін нүктеге сәйкес келетін
соңғы аппроксимациясы бөлік-үзіліссіз беттердің жиынтығы ретіде болады, яғни олардың әрбіреуі түйін нүктеге сәйкес келетін
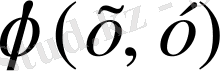 мәнінің көмегімен бөлек элементте анықталған .
мәнінің көмегімен бөлек элементте анықталған .
Ақырлы элементтер әдісінің маңызды аспектісі элемент функциясын анықтау кезінде элементтер ішінен типті элементті бөліп алу мүмкіндігі болады. Бұл элемент функциясын жалпы байланысқан моделдегі элементтің орнына қатысты немесе басқа элемент функциясына тәуелсіз анықтауға болатынын көрсетеді. Элемент функциясының түйін мәндерінің кез келген жиыны және координаталары арқылы берілуі элемент функциясын облыс геометриясының аппроксимациясы үшін қолдануға болатынын білдіреді.
Қазіргі уақытта ақырлы элемменттер әдісін қолдану облысы өте кең және дифференциал теңдеулермен сипаттала алатын барлық физикалық есептерді қамтиды. Ақырлы элементтер әдісінің ең маңызды артықшылықтары, яғни осы артықшылықтары мен ол кең қолданысқа ие:
- Сыбайлас әлемнің материалдарының қасиеті міндетті түрде бірдей болмаса да болады. Бұл әдісті әртүрлі материалдардан жасалған денелерге де қолдануға болатынын көрсетеді.
- Қисықсызықты облыс қисықсызықты элементтің көмегімен аппроксимацияланады немесе қысықсызықты элементтің көмегімен дәл сипатталады. Осылайша, әдісті шекарасы « жақсы» облыстар үшін ғана емес басқа да облыстар үшін қолдануға болатынын көрсетеді.
- Элементтер өлшемі айнымалыда бола алады. Бұл облысты элементтерге бөлу желісі үлкейіп немесе кішірейіп кетуіне әсер етуі мүмкін, егер оның қажеттілігі болса.
- Ақырлы элементтер әдісінің көмегімен үзілісті беттердегі шекаралық шарттарды сонымен бірге аралас шекаралық шарттарды қарастыруға еш қиындық туғызбайды.
- Жоғарыда көрсетілген ақырлы элементтер әдісінің артықшылықтары анықталған кластың кейбір есептері үшін жеткілікті жалпы программасын құруда қолданылады. Мысалы, жылу таралу туралы өстік ассимметриялық есептер үшін программаның көмегімен осы типті есептердің кез келгенін шешуге болады. Ақырлы элементтер әдісімен шығарылатын есептердің кеңейтудегі кедергі болатын фактор, ол машина жадының шектеулілігі және есептеу жұмыстарының құнының жоғары болуында.
Ақырлы элементтер әдісінің ең басты кемшілігі есептеу программасын құрудың немесе есептеу техникасын қолданудың қажеттілігінде.
Ақырлы элементтер әдісін қолданудағы есептеулер қолмен есептеу жүргізуге өте күрделі, ең қарапайым есептері үшін де. Күрделі есепті шешу үшін өте үлкен жад тез қозғалатын ЭЕМ-рын қолдану керек.
§1. 2 Сызық интерполяциялық полиномдар
Ақырлы элементтер класификациясы осы элементтің полиномды функция ретімен сәйкес жүргізілді. Сонымен бірге келесі үш элементтер топтары қарастырылады: симплекс, комплекс және мультиплекс- элементтер. Симплекс элементке құрамында тұрақты және сызықты мүшелері бар полиномдар сәйкес келеді. Мұндай полиномдардағы коэфициенттер саны координатты кеңістік өлшемінен бір бірлікке үлкен (көп) болады.
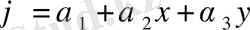
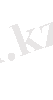 (1. 2. 1)
(1. 2. 1)
Полиномы екі өлшемді үшбұрышты элнмент үшін симплексті функцияны береді. Бұл полином х және у бойынша сызықты және үш коэфициенті бар, себебі үшбұрыштың үш түйіні бар.
Комплекс элементтерге құрамында тұрақты, сызықты мүшесі, сонымен қатар екінші, үшінші және қажет болған жағдайда одан да жоғары ретті полиномды функция сәйкес келеді.
Комплекс- элементтер формасы симплекс-элементтер формасы сияқты, бірақ комплекс-элементтер қосымша шекаралық түйіндер болады, сонымен қатар оларды ішкі түйіндер де болуы мүмкін. Симплекс және комплекс-элементтердің басты айырмашылығы, комплекс-элементтердегі түйіндер саны координаталық кекеңістік өлшеміне бір бірлік қосқанға тең шамадан үлкен болады. Екі өлшемді үшбұрышты комплекс -элемент үшін интерполяциялық полином мына түрде болады:
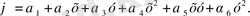 (1. 2. 2)
(1. 2. 2)
Бұл қатынаста алты коэфицент кіреді, сондықтан қарастырылатын элементтің түйіні болуы керек.
Мультиплекс элементтер үшін де құрамында жоғарғы ретті мүшелері бар полиномдар қолданылады, бірақ элементтер шекарасы, осы кезде бір элементпен екінші элементке орын ауыстырғанда үзіліссіздікке қол жеткізу қажет кордината осьтеріне, паралель болуы керек. Симплекс және комплекс-элементтер шекараларында мұндай шектеу болмайды.
У
Х
1. 1-сурет. Тіктөртбұрыш, екіөлшемді мултиплекс элемент.
1. 1-суретте көрсетілген төртбұрышты элемент осы мультиплекс-элементтердің тамаша мысалы.
Мұнда симплекс-элементтер қарастырылады. Комплекс және мультеплекс элементтерді кітаптың қолданбалы бөлімінен кейін изопараметрлік элементтермен қатар қарастырамыз.
§ 1. 2. Бірөлшемді симплекс-элемент.
Бірөлшемді симплекс-элементке әрбір ұшында бір-бірден екі түйіні бар. ұзындығы L болатын түзу сызықты кесіндіні береді. (3. 2-сурет) .
У

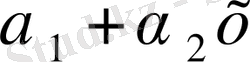
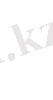
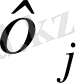
j
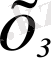 i L х
i L х

3. 2-сурет. Бірөлшемді симплекс-элемент.
Түйіндер і және ј индекстерімен, ал түйіндік мәндер сәйкес
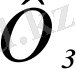 және
және
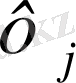 арқылы белгіленеді. Координаталар жүйесінің басы элементтен тыс орналасады. Скаляр шама үші полиномды функция мына түрде болады
арқылы белгіленеді. Координаталар жүйесінің басы элементтен тыс орналасады. Скаляр шама үші полиномды функция мына түрде болады
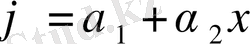 (1. 2. 3)
(1. 2. 3)
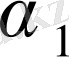 және
және
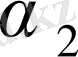 кофиценттері түйін нүктелеріндегі шарттардың көмегімен анықталуы мүмкін:
кофиценттері түйін нүктелеріндегі шарттардың көмегімен анықталуы мүмкін:
 болғанда
болғанда

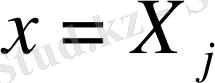 болғанда
болғанда
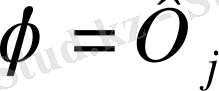 .
.
Бұл түйіндік шарттар екі теңдеулер жүесіне алып келеді
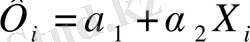
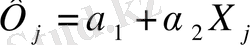
Ал оның шешімі былай болады
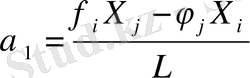 (1. 2. 4а)
(1. 2. 4а)
және
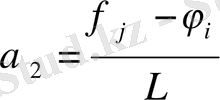 (1. 2. 4б)
(1. 2. 4б)
Табылған
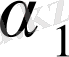 және
және
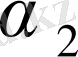 мәндерін (1. 2. 3) -формулаға қойып,
мәндерін (1. 2. 3) -формулаға қойып,
 үшін мынадай өрнек аламыз :
үшін мынадай өрнек аламыз :
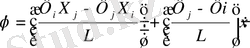 ,
,
яғни оны мына түрде қайта жазуға болады:
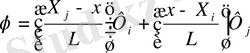 (1. 2. 5) .
(1. 2. 5) .
(1. 2. 5) формуладағы х-тің сызықты функцияларын функция формалары немесе интерполяциялық функциялар деп атайды. Бұл функциялар барлық жерде N арқылы белгіленеді . Әрбір форма функциясы өзіне қатысты түйінді белгілеу үшін, төменгі индекспен жазылу керек. Кез келген функция формасын
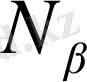 арқылы белгілейміз. (1. 2. 5) қатынасына келесі функция формалары енеді :
арқылы белгілейміз. (1. 2. 5) қатынасына келесі функция формалары енеді :
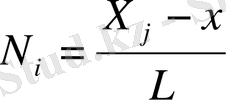 және
және
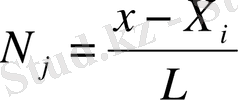
- қатынасын матрицалық матрицалық түрде жазуға да болады:
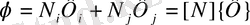 (1. 2. 6)
(1. 2. 6)
Мұндағы
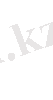
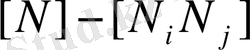
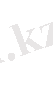 -матрицалық қатар және
-матрицалық қатар және
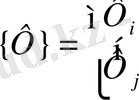 -баған- вектор. Ендеше (1. 2. 5) формуладан,
-баған- вектор. Ендеше (1. 2. 5) формуладан,
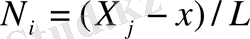 функциясы і-ші номерлі түйінде бірге тең, және j-ші түйінде нольге тең. Осылайша
функциясы і-ші номерлі түйінде бірге тең, және j-ші түйінде нольге тең. Осылайша
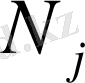 функциясы і-ші түйінде нольге және j-ші номерлі түйінде бірге тең. Олар бір анықталған түйінде ғана бірге тең де, және басқа барлық түйіндерде нольге айналады .
функциясы і-ші түйінде нольге және j-ші номерлі түйінде бірге тең. Олар бір анықталған түйінде ғана бірге тең де, және басқа барлық түйіндерде нольге айналады .
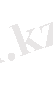
II Тарау . Қатты дененің деформацияланған
механикасы. Серпімділік теориясы.
§ 2. 1. Ақырлы элементтер әдісінің теңдеуі:өрістер
теориясының есептері.
Алдыңғы бөлімдерде қарастырғандай, жылу таралудың бірөлшемді есебі дербес туындылы дифференциал теңдеулермен сипатталатын кейбір маңызды физикалық есептердің бірі болады. Осы физикалық процестердің әрбіреуі үшін дифференциал теңдеуі жалпы алғанда квазигормониялық теңдеулерге жатады:
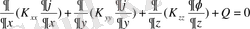 (2. 1. 1) .
(2. 1. 1) .
шекаралық шарттары бар:
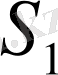 -де
-де
 (2. 1. 2) .
(2. 1. 2) .
және (немесе)
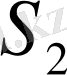 -де
-де
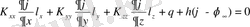 (2. 1. 3) .
(2. 1. 3) .
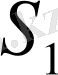 және
және
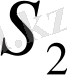 нің бірігуі толық шекараны береді.
нің бірігуі толық шекараны береді.
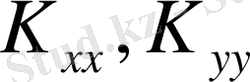
 және
және
 коффиценттері, сонымен бірге q шамасы x, y және z -тің функциялары болуы мүмкін,
коффиценттері, сонымен бірге q шамасы x, y және z -тің функциялары болуы мүмкін,
 дан тәуелсіз ек
дан тәуелсіз ек
 ендігі ескеріледі. (2. 1. 3) формуладағы
ендігі ескеріледі. (2. 1. 3) формуладағы
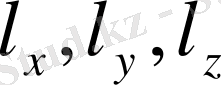 шамалары-бетке тұрғызылған нормал вектордың бағытта
шамалары-бетке тұрғызылған нормал вектордың бағытта
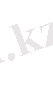 ұшы косинустары. (2. 1. 1) теңдеуі изотропты денелерге де анизатропты денелерге де қолданылады. Бірақ, координаталық осьтер, анизатропты облыстағы инерция басты өсіне паралел болуы керек .
ұшы косинустары. (2. 1. 1) теңдеуі изотропты денелерге де анизатропты денелерге де қолданылады. Бірақ, координаталық осьтер, анизатропты облыстағы инерция басты өсіне паралел болуы керек .
(2. 1. 1) теңдеу шекаралық шарттарымен қоса үшөлшемді облыстағы жылудың таралуын сипаттайды. Бұл жағдайда
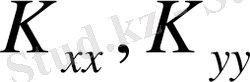 және
және
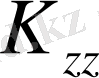 коэффиценттері жылу өткізгіштіктің коэффицеттері сәйкестенеді, Q -ішкі жылу көзі немесе ағу, q- беттің бөлігіндегі жылу ағыны және h-жылу ауысу коэффицеттері .
коэффиценттері жылу өткізгіштіктің коэффицеттері сәйкестенеді, Q -ішкі жылу көзі немесе ағу, q- беттің бөлігіндегі жылу ағыны және h-жылу ауысу коэффицеттері .
 өріс функциясы дене температурасын анықтайды . жылу таралудың бірөлшемді және екі өлшемді жағдайлары үшін теңдеуді (1. 1. 1) формуладан
өріс функциясы дене температурасын анықтайды . жылу таралудың бірөлшемді және екі өлшемді жағдайлары үшін теңдеуді (1. 1. 1) формуладан
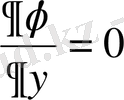 және
және
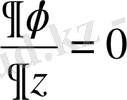 деп есептеп алуға болады. Егер
деп есептеп алуға болады. Егер
 анықталмаған шекараның бөлігінде (
анықталмаған шекараның бөлігінде (
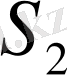 -де) q және h екі шамалар нольге тең болса, (2. 1. 3) теңдік келесі шартқа келтіріледі:
-де) q және h екі шамалар нольге тең болса, (2. 1. 3) теңдік келесі шартқа келтіріледі:
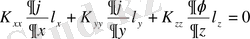 (2. 1. 4)
(2. 1. 4)
Яғни жылудың алмасудың жоқ болмайтынына әсерін тигізеді. Ары қарай шекараның барлығында
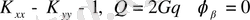 болғандағы екі өлшемді жағдайын қарастырамыз. Бұл жағдайда (2. 1. 1) теңдеуі келесі теңдеуге келтіріледі:
болғандағы екі өлшемді жағдайын қарастырамыз. Бұл жағдайда (2. 1. 1) теңдеуі келесі теңдеуге келтіріледі:
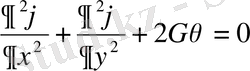 (2. 1. 5)
(2. 1. 5)
Яғни серпімді стерженнің дөңгелек емес қимасын бурау туралы есебінде кездеседі .
 өріс функциясы енді кернеу функциясы болады, G-материалдық серпімді сипаттамасы,
өріс функциясы енді кернеу функциясы болады, G-материалдық серпімді сипаттамасы,
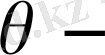 стержень қимасын бурау бұрышы. Ішкі бурау күшінен пайда болған қозғалыс кернеуі
стержень қимасын бурау бұрышы. Ішкі бурау күшінен пайда болған қозғалыс кернеуі
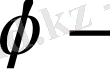 ді х және у бойынша дифференциалдағаннан алынады.
ді х және у бойынша дифференциалдағаннан алынады.
Басқа маңызды екі өлшемді есепке сұйықтың құйынсыз ағыны туралы есеп жатады. Бұл мысалда
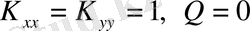 және (2. 1. 1) теңдеуі
және (2. 1. 1) теңдеуі
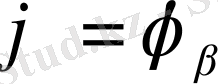 шекаралық шарттары бар мынау теңдеуге келтіріледі:
шекаралық шарттары бар мынау теңдеуге келтіріледі:
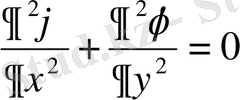 (2. 1. 6)
(2. 1. 6)
және
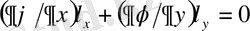 . Егер
. Егер
 өріс функциясы облыстың өтпейтін шекарараларында берілсе (сұйықтың ағыны болмайтын нормалі бойынша шекараларында ), онда (2. 1. 6) теңдеу сұйық ағынның құйынсыз болғандағы токтың сызығын анықтайды. Басқаша айтқанда, егер өріс функциясы сұйықтың ағынынң нормалі бойынша алынған шекаралардың бөлігінде анықталған болса, онда (2. 1. 6) теңдеу ток сызығына ортагональ болатын эквипотенциал сызықтарды сипаттайды.
өріс функциясы облыстың өтпейтін шекарараларында берілсе (сұйықтың ағыны болмайтын нормалі бойынша шекараларында ), онда (2. 1. 6) теңдеу сұйық ағынның құйынсыз болғандағы токтың сызығын анықтайды. Басқаша айтқанда, егер өріс функциясы сұйықтың ағынынң нормалі бойынша алынған шекаралардың бөлігінде анықталған болса, онда (2. 1. 6) теңдеу ток сызығына ортагональ болатын эквипотенциал сызықтарды сипаттайды.
Жер астындағы суларының шектелген ағыны үшін дифференциал теңдеу (2. 1. 1) те де бар. Бұл жағдайда
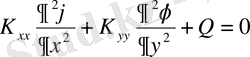 (2. 1. 7)
(2. 1. 7)
Ал шекаралық шарттар мына түрде болады
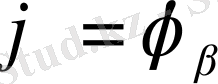 және (немесе)
және (немесе)
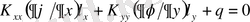 .
.
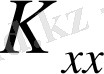 және
және
 коэффиценттері топыраққа өтімділігін (өткізгіштігін ) анықтайды, Q -су көзі, ал
коэффиценттері топыраққа өтімділігін (өткізгіштігін ) анықтайды, Q -су көзі, ал
 -өріс функциясы-пьезометричиский қысым . qшамасы су өткізетін қабат арқылы оның шекараларының бөліктері бойымен судың ағып жиналуына сәйкес келеді.
-өріс функциясы-пьезометричиский қысым . qшамасы су өткізетін қабат арқылы оның шекараларының бөліктері бойымен судың ағып жиналуына сәйкес келеді.
(2. 1. 1) теңдеуімен сипатталатын басқа маңызды физикалық есептер электростатикалық және могнитетолникалық өрістерді сонымен қатар сұйық майлайтын плёнкаларды да қарастырғанмен байланысты.
(2. 2) және (2. 3) шекаралық шарттары бар (2. 1) теңдеуді варицалық көзқарасымен шешу, мына функционалдық минимумын іздеуге эквивалентті
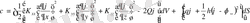 (2. 1. 8)
(2. 1. 8)
(2. 1. 8) функционалдық минимизациясы
 түйін мәндерінің жиынында қабылданған болуы керек . осы мақсатпен алдыңғы бөлімді қарастырғандай, атап айтқанда (2. 1. 8) функционалын интегралдау алдында минимизациялайтын процедурасын қолданамыз. Бұл амал түрлендіруден амал әрбір тиянақты есептер үшін қолайлырақ элементтер характеристикасын таңдауға мүмкіндік береді.
түйін мәндерінің жиынында қабылданған болуы керек . осы мақсатпен алдыңғы бөлімді қарастырғандай, атап айтқанда (2. 1. 8) функционалын интегралдау алдында минимизациялайтын процедурасын қолданамыз. Бұл амал түрлендіруден амал әрбір тиянақты есептер үшін қолайлырақ элементтер характеристикасын таңдауға мүмкіндік береді.
Минимизация процесін (2. 1. 8) фнукционалын түрлендіруден бастаймыз. бұл қадам келесі операцияларды қысқартарады. Екі матрица енгіземіз:
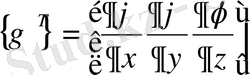 (2. 1. 9)
(2. 1. 9)
және
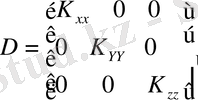 (2. 1. 10)
(2. 1. 10)
(2. 1. 8) қатнасы енді мына түрде жазылады:
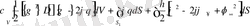 (2. 1. 11)
(2. 1. 11)
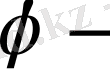 функциясы облыстың барлық жерінде үзіліссіз болмайтынын ескерсек, оның орнына бөлек элементтерде анықталған
функциясы облыстың барлық жерінде үзіліссіз болмайтынын ескерсек, оның орнына бөлек элементтерде анықталған
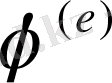 функциясын қарастыруын негіземіз. (2. 1. 11) дегі интегралдары бөлек элементтер бойынша алынған интегралдарға бөлінуі керек, яғни
функциясын қарастыруын негіземіз. (2. 1. 11) дегі интегралдары бөлек элементтер бойынша алынған интегралдарға бөлінуі керек, яғни
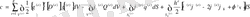 (2. 1. 12)
(2. 1. 12)
мұндағы
 -элементтердің жалпы саны. Соңғы қатынасты былайша жазуға да болады:
-элементтердің жалпы саны. Соңғы қатынасты былайша жазуға да болады:
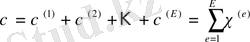 (2. 1. 13)
(2. 1. 13)
Мұндағы
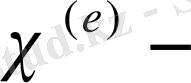
 дағы бөлек элементтің үлесі
дағы бөлек элементтің үлесі
 минимизациясы мына қатынастың орындалуын талап етеді:
минимизациясы мына қатынастың орындалуын талап етеді:
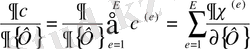 (2. 1. 14)
(2. 1. 14)
(2. 1. 14) -дегі
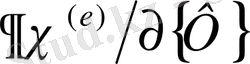 дербес туындылары, (2. 1. 12) -дегі интегралдар
дербес туындылары, (2. 1. 12) -дегі интегралдар
 түйіндік мәндер арқылы өрнектелмейінше анықталған бола алмайды. мына қатынасты ескеріп:
түйіндік мәндер арқылы өрнектелмейінше анықталған бола алмайды. мына қатынасты ескеріп:
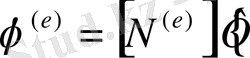 (* ) (2. 1. 8) шамасын есептеуге болады, яғни (*) орнына (2. 12) қойылуы мүмкін .
(* ) (2. 1. 8) шамасын есептеуге болады, яғни (*) орнына (2. 12) қойылуы мүмкін .
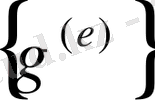 үшін өрнек жазамыз.
үшін өрнек жазамыз.
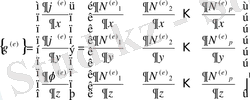 (2. 1. 15)
(2. 1. 15)
немесе
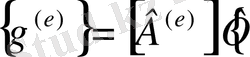 (2. 1. 16)
(2. 1. 16)
мұндағы
 - форма функциясының туындысымен байланысты информациясы бар. Бұл шамалар әзірше белгісіз, сондықтан себебі форма функциясы әлі анықталмаған. (*) және (2. 1. 16) формулаларын қолдану мына түрдегі (2. 1. 12) -ң элементтері бойынша алынған интегралдарды жазуға болатынын білдіреді:
- форма функциясының туындысымен байланысты информациясы бар. Бұл шамалар әзірше белгісіз, сондықтан себебі форма функциясы әлі анықталмаған. (*) және (2. 1. 16) формулаларын қолдану мына түрдегі (2. 1. 12) -ң элементтері бойынша алынған интегралдарды жазуға болатынын білдіреді:
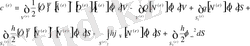 (2. 1. 17)
(2. 1. 17)
 және
және
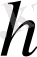 шамалары белгісіз коэффиценттер. Олар интегр
шамалары белгісіз коэффиценттер. Олар интегр
 ал таңбасының астына енген. себебі олар элемент ішінде өзгеруі мүмкін.
ал таңбасының астына енген. себебі олар элемент ішінде өзгеруі мүмкін.
 бойынша (2. 1. 17) шамасын дифференциалдау, егер Б қосымшасында келтірілгендей дифференциалдау ережелерін қолданса, онда типті қарапайым операциялардаы білдіреді. (2. 1. 17) формуланы қарастырамыз:
бойынша (2. 1. 17) шамасын дифференциалдау, егер Б қосымшасында келтірілгендей дифференциалдау ережелерін қолданса, онда типті қарапайым операциялардаы білдіреді. (2. 1. 17) формуланы қарастырамыз:
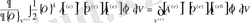
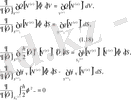
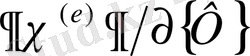
 , бөлек элементтің
, бөлек элементтің
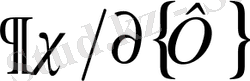 -кежалпы қосындыға үлесі мынаған тең :
-кежалпы қосындыға үлесі мынаған тең :
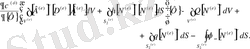
(2. 1. 19)
Бұл интегралдар жиынтығын қысқаша мына түрде жазуға болады :
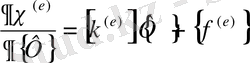 (2. 1. 20)
(2. 1. 20)
мұндағы
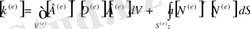 (2. 1. 21)
(2. 1. 21)
және
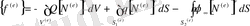 (2. 1. 22)
(2. 1. 22)
Соңғы теңдеулер жүйесі (2. 1. 13) -ге (2. 1. 20) өрнегін апарып қойғаннан кейін алынады:
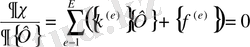 (2. 1. 23)
(2. 1. 23)
немесе
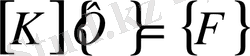 (2. 1. 24)
(2. 1. 24)
мұндағы
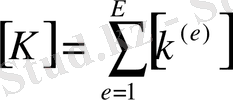 (2. 1. 25)
(2. 1. 25)
және
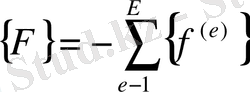 (2. 1. 26)
(2. 1. 26)
(2. 1. 21) -дегі интегралдар
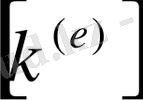 элементінің матрицасын, ал (2. 1. 22) -дегі интегралдар
элементінің матрицасын, ал (2. 1. 22) -дегі интегралдар
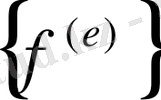 элементінің күшінің векторын анықтайды. Бұл интегралдар осы бөлімдің негізгі нәтіжелерін береді.
элементінің күшінің векторын анықтайды. Бұл интегралдар осы бөлімдің негізгі нәтіжелерін береді.
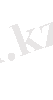 §
2. 2. Ақырлы элементтер әдісінің теңдеуі:серпімділік
§
2. 2. Ақырлы элементтер әдісінің теңдеуі:серпімділік
теориясы.
Серпімділік теориясының есептерін шешу келесі екі әдістің бірімен жүргізілуі мүмкін. Бірінші әдістің көмегімен берілген шекаралық шарттары бар дифференциал теңдеу шешіледі. Екінші әдіс түсірілген күштің және кернеудің жұмысымен байланысқан интегралды шаманың минимизациясына негізделген . серпімділік теориясының есептерін ақырлы элементтер әдісімен шешу үшін соңғы әдіс қолданылады. Егер есеп шығарылса орын ауыстырумен немесе шекараларында олардың мәндері берілген болса, онда жүйенің потенциал энергиясын минимизациялау керек. Егер есеп шекараларында берілген күш салудың кернеуімен шешілсе онда жүйенің қосымша жұмысын минимизациялау керек. Ақырлы элементтер әдісінің жалпыға бірдей қабылданған формулировкасы орын ауыстыру өрісін іздеу және сонымен бірге орынауыстыру векторларының түйін мәндерін іздеген кездегі потенциал энергияның жүесінің минимизасиясымен байланысқан. Содан кейін орын ауыстыру анықталған бойда кернеумен деформацияның тензорларының компанеттерін есептеуге боладвы.
Бұдан ары қарай біз потенциалдар энергиясының минимищасиясына байланысты, ақырлы элементтер әдісін қолданатын болғандықтан, осында потенциалдар энергиясы туралы теореманы келтіреміз.
Кинематикалық шекаралық шарттарды қанағаттандыратын барлық орын ауыстырулардан, потенциал энергияның стационар мәндері теңдестік теңдеуін қанағаттандыратын
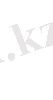 орын ауыстырулар ғана қатынасады.
орын ауыстырулар ғана қатынасады.
Бұл теореманың басты талабы іздеп отырған орын ауыстуруымыз шекараларда берілген мәндерді қанағаттандыру керек екен. Серпімді жүенің толық потенциал энергияларымен анықталады. Осыларға сәйкес толық энергияны мына түрде жазамыз:
 (2. 2. 27)
(2. 2. 27)
мұндағы
 -деформация энергиясы, ал
-деформация энергиясы, ал
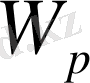 - түсірілген күштің потенцил энергиясы. Сыртқы күштің жұмысы таңбасы бойынша олардың потенциалдар энергиясына қарама-қарсы :
- түсірілген күштің потенцил энергиясы. Сыртқы күштің жұмысы таңбасы бойынша олардың потенциалдар энергиясына қарама-қарсы :
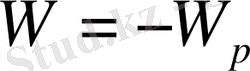 (2. 2. 28)
(2. 2. 28)
(2. 2. 27) және (2. 2. 28) формулалардан алатынымыз:
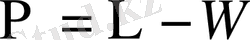 (2. 2. 29)
(2. 2. 29)
Облысты элементтерге бөлгенне кейін, (2. 2. 29) теңдік қосынды түрінде жазылады:
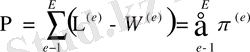 (2. 2. 30)
(2. 2. 30)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz