Нақты сан

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Нақты сан

Нақты сан - кез келген оң, теріс және нөл сандары. Ол рационал сандар және иррационал сандар болып бөлінеді. Нақты сан түсінігі рационал сан ұғымын кеңейтуден шыққан. Кеңейтудің қажеттілігі кез келген шаманың мәнін толық анықталған сан көмегімен өрнектеуден және математиканың ішкі дамуынан пайда болды. Мысалы: сандарға орындалатын бірсыпыра амалдарды пайдалану облысын кеңейту (түбір астынан шығару, логарифмдерді есептеу, теңдеулерді шешу және т. б. ) . Нақты сандардың жалпы ұғымын ертедегі грек математиктері салыстырып өлшеуге болмайтын кесінділер теориясында берді. Жүйелі теорияны тек 19 ғасырдың соңында Г. Кантор, Р. Дедекинд және К. Вейерштрасс жасады. Барлық нақты сандар жиыны сан түзуі деп аталады және деп белгіленеді. сызықты реттелген жиын және негізгі арифмет. амалдарға (қосу мен көбейту) қатысты өріс құрады. Сан түзуі геометриялық түзуге ұқсас, былайша айтқандадегі сандар мен түзудегі нүктелер арасында реттілігі сақталатын өзара бірмәнді сәйкестік орнатуға болады. Осы сәйкестіктен сан түзуінің үздіксіздігі шығады. Түзудің үздіксіздігі жөніндегі қағида қазіргі матем. талдаудың негізі болып табылады.

1 . Натурал сандар

Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4, …

Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈ N, 5 ∈ N, 3 ∈ N.

2. Бүтін сандар

Бүтін сандар деп оң және теріс таңбасымен алынған барлық натурал сандар жиынынан құралған сандар жиының атаймыз.

Яғни бүтін сандар 0, 1, 2, 3, 4, … және -1, -2, -3, -4, … сандар жиындарының бірігуінен құралған. Бүтін сандар жиының P символымен белгілейміз.

Тұжырым.

N жиынына еңетің кез келген сан P жиынына да еңеді. Бұндай жағдайда N жиыны P жиынына еңеді дейді, және N ⊆ P деп жазады.

Сұрақ.

P жиыны N жиынына еңеді ме?

3. Рационал сандар

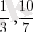Рационал сандар деп (a ∈ P, b ∈ P, b ≠ 0) сандарын атаймыз. Мысалы нақты сандар . Рационал сандар жиының R деп белгілейміз.

Кез келген бүтін c саны рационал жиынына еңеді да, яғни рационал саны да болып табылады. Өйткені 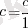, соңдықтан P ⊆ R.

Сұрақ.

N ⊆ R тұжырымы орынды ма?

4 . Иррационал сандар

Иррационал сан деп π = 3, 141592… немесе 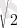иррационал сандар = 1, 4… сандары тәрізді бөлшек бөлігі шексіз, периодты емес цифрлардан құралған сандарды атаймыз.

Иррационал сандар жиының Q деп белгілейміз.

5. Нақты сандар

Нақты сандар жиыны деп барлық- натурал, бүтін, рационал және иррационал сандардан құралған сандар жиының атаймыз. Және бұл жиынды Z әрпімен белгілейміз.

Иррационал сандар

Бұдан ертерек айтылғандай, сан түзуінде көптеген рационал сандар бар. Енді сан түзуіндегі кез келген нүкте рационал сан ретінде көрсетіле алады ма екенін тексерейік.

Мысалы, екі бүйірінің ұзындықтары 1-ге тең болатын тең бүйірлі тікбұрышты үшбұрыштың гипотенузанысының ұзындығы x болсын.

Пифагор теоремасын қолдансақ;

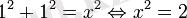
$1^2+1^2=x^2\Leftrightarrow x^2=2$

説明文

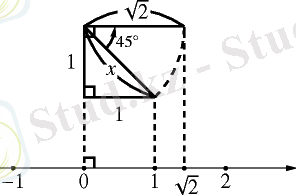
Сондықтан, ұзындығы 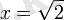$x=\sqrt{2}$ және бұл графиктегідей көрсетіле алады.

Жиын. Логикалық символдар. Нақты сандар және олардың қасиеттері. Сандардың абсолют шамасы.

Математикалық анализ дерлік кез-келген математикалық пәннің негізі болатын классикалық математиканың бөлігі.

«Математикалық анализ» курсы белгілі белгілі білім қорын жеткізіп және оларды қолдануға үйретіп қана қоймай, ол сонымен қатар математиканы оқып-үйрену үшін қажетті студенттердің логикалық ойлауын және математикалық мәдениетін дамытады.

«Математикалық анализ» пәні жалпы ғылыми пән болып табылады - ол студенттерді басқа математикалық пәндерді оқып үйренуге дайындайды.

Математикалық анализді табысты меңгеру үшін орта мектеп көлеміндегі элементарлық математиканы, сондай-ақ қатар оқылатын жоғарғы және сызықтық алгебраны, аналитикалық геометрияны білу қажет.

Бұл пәннің оқып - зерттеу объектісі алдымен функциялар болып келеді.

Функциялардың көмегі арқылы табиғатты және техникадағы болатын әр түрлі процестердің заңдары тұжырымдалады.

«Математикалық анализ» пәнінің мақсаты шексіз аздарды таңдаудың негізін құрайтын дифференциалдық методтарымен студенттерді таныстыру.

1. Нақты сандар. Рационал және иррационал сандардың жиынын нақты сандар дейді. Нақты сандарды Ох-сандар өсінде нүкте арқылы кескіндейді. Әрбір нақты санға сандар өсінде анықталынған белгілі бір нүкте, керісінше, сандар өсіндегі әрбір нүктеге анықталынған белгілі бір нақты сан сәйкес келеді. Нақты сандарды R немесе (-¥, +¥) символдарымен белгілейді.

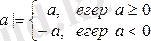
қатынаспен анықталатын теріс емес санын нақты сан -ның абсолют шамасы дейді.

Санның абсолют шамасының қасиеттері:

1. ; 2. ;

3. ; 4. ;

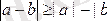5. ; 6. ;

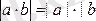7. .

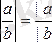Х0 нүктесінің e (e>0) төңірегі деп(х0-e; х0+e) аралығын немесе x-x0<e теңсіздігін қанағаттандыратын нақты сандар жиынын айтады.

2. Функция және оның берілу тәсілдері. Егер әрбір xÎD эле-ментіне анықталынған белгілі бір уÎЕэлементі сәйкестендіріл-се, онда у-ты х-тыңфункциясы деп атайды да, былай белгілейді: 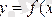( 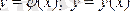, т. с. с. ) . Мұнда х-тәуелсіз, ал у -тәуелді айнымалы деп аталады. 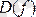функцияның анықталу облысы, ал 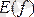функция мәндерінің жиыны делінеді. Функция аналитикалық(формуламен), таблицалық, графикалықтәсілдермен беріледі.