Сызықты, нормаланған және Гильберт кеңістіктері: операторлар теориясы және Штурм-Лиувилль операторы үшін компакт әдіс


Жоспар
Кіріспе.
- Кеңістіктер мен операторлар ұғымы. 1. 1. Сызықты кеңістіктің жалпы анықтамасы. 1. 2. Нормаланған кеңістік. 1. 3. Метрикалық кеңістік. 1. 4. Гильберт кеңістігі. 1. 5. Сызықты оператор және оның қасиеттрі. 1. 6. Тұйық оператор және оның қасиеттрі.
- Штурм-Лиувилль операторы үшін компакт әдісінің қолданылуы2. 1. Штурм-Лиувилль операторы және оның қасиеттері. 2. 2 Штурм-Лиувилль операторы үшін компакт әдісінің қолданылуы
- Қорытынды.
- Пайдаланылған әдебиеттер.
I. Кеңістіктер мен операторлар ұғымы.
1. 1.
Сызықты кеңістіктің жалпы анықтамасы
 сызықты кеңістік деп
сызықты кеңістік деп
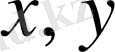 элементтерінің төмендегі жиынтығын айтады: I.
элементтерінің төмендегі жиынтығын айтады: I.
 -де 1. Егер
-де 1. Егер
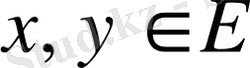 болса, онда
болса, онда
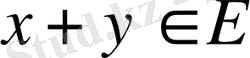 ; 2.
; 2.
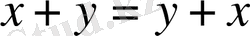 ; 3.
; 3.
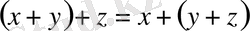 ; 4.
; 4.
 -де барлық
-де барлық
 үшін
үшін
 болатын “нөлдік” 0 бар болады. Жоғарыдығы қасиеттерді қанағаттандыратын кез-келген
болатын “нөлдік” 0 бар болады. Жоғарыдығы қасиеттерді қанағаттандыратын кез-келген
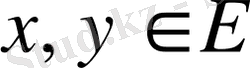 элеметттері үшін
элеметттері үшін
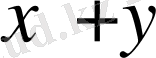 қосындысы
қосындысы
 -де анықталған. II.
-де анықталған. II.
 -де
-де
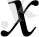 элементінің
элементінің
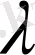 санына көбейтіндісі
санына көбейтіндісі
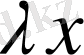 анықталған және ол мына қасиеттерге ие болады: 5. Егер
анықталған және ол мына қасиеттерге ие болады: 5. Егер
 болса, онда
болса, онда
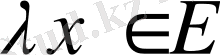 ; 6.
; 6.
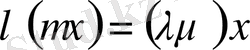 ; 7.
; 7.
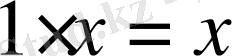 ; 8.
; 8.
 (сол жағында 0 саны, ал оң жағында нөлдік элемент) ; 9.
(сол жағында 0 саны, ал оң жағында нөлдік элемент) ; 9.
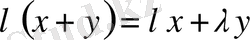 ; 10.
; 10.
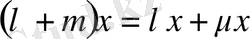 ; Мұнда
; Мұнда
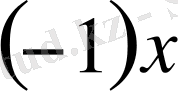 элементі
элементі
 арқылы белгіленеді. 7, 10, 8 қасиеттерінен
арқылы белгіленеді. 7, 10, 8 қасиеттерінен
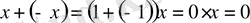 шығатынын көреміз.
шығатынын көреміз.
 кеңістігінің
кеңістігінің
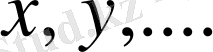 элементтері оның векторлары деп аталады. Сызықты кеңістікте
элементтері оның векторлары деп аталады. Сызықты кеңістікте
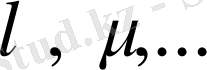 (скалярды) сандық көбейткіштер ретінде нақты немесе комплексті сандар алынады. Бірінші жағдайда
(скалярды) сандық көбейткіштер ретінде нақты немесе комплексті сандар алынады. Бірінші жағдайда
 нақты сызықты кеңістік, ал екінші жағдайда комплекстік сызықты кеңістік деп аталады. Сызықты кеңістіктерге сызықты тәуелді мен тәуелсіз векторлар ұғымы енгізіледі.
нақты сызықты кеңістік, ал екінші жағдайда комплекстік сызықты кеңістік деп аталады. Сызықты кеңістіктерге сызықты тәуелді мен тәуелсіз векторлар ұғымы енгізіледі.
 кеңістігінің
кеңістігінің
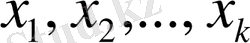 векторлары сызықты тәуелсіз деп аталады, егер
векторлары сызықты тәуелсіз деп аталады, егер
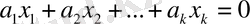
 Equation. 3 теңдігінен
Equation. 3 теңдігінен
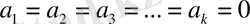 болса. Кері жағдайда (яғни,
болса. Кері жағдайда (яғни,
 Equation. 3 теңдігінде ең болмағанда
Equation. 3 теңдігінде ең болмағанда
 коэффициентінің біреуі нөлден өзгеше болады)
коэффициентінің біреуі нөлден өзгеше болады)
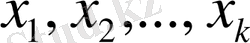 векторлары сызықты тәуелді деп аталады. Егер де
векторлары сызықты тәуелді деп аталады. Егер де
 кеңістігінде
кеңістігінде
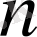 сызықты тәуелсіз векторлар бар болып, ал кез-келген
сызықты тәуелсіз векторлар бар болып, ал кез-келген
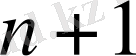 векторлар сызықты тәуелді болса, онда
векторлар сызықты тәуелді болса, онда
 кеңістігінің өлшемі
кеңістігінің өлшемі
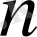 тең. Егер
тең. Егер
 кеңістігіндегі кез-келген
кеңістігіндегі кез-келген
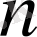 үшін
үшін
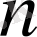 сызықты тәуелсіз векторлар бар болады, онда
сызықты тәуелсіз векторлар бар болады, онда
 кеңістігінің өлшемі шексіздіке тең болады.
кеңістігінің өлшемі шексіздіке тең болады.
 -
-
 кеңістігінен алынған векторлар болсын. Онда
кеңістігінен алынған векторлар болсын. Онда
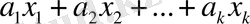 түріндегі кез-келген мүмкін болатын сызықты комбинациялар
түріндегі кез-келген мүмкін болатын сызықты комбинациялар
 кеңістігінің ішкі кеңістігін құрайды. Оның өлшемі
кеңістігінің ішкі кеңістігін құрайды. Оның өлшемі
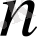 -нен үлкен емес.
-нен үлкен емес.
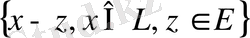 түріндегі жиынды (мұндағы
түріндегі жиынды (мұндағы
 кеңістігінің ішкі кеңістігі, ал
кеңістігінің ішкі кеңістігі, ал
 алынған, белгіленген элемент) сызықты көп бейне деп аталады.
Мысал 1.
алынған, белгіленген элемент) сызықты көп бейне деп аталады.
Мысал 1.
 түзу сызығы, яғни, қарапайым арифметикалық қосу және көбейту амалдары орындалатын нақты сандар жиыны сызықты кеңістік болады.
Мысал 2.
Қарапайым функцияларды қосу және оларды санға көбейту амалдары орындалатын үздіксіз (нақты емес комплексті) функциялар кез-келген
түзу сызығы, яғни, қарапайым арифметикалық қосу және көбейту амалдары орындалатын нақты сандар жиыны сызықты кеңістік болады.
Мысал 2.
Қарапайым функцияларды қосу және оларды санға көбейту амалдары орындалатын үздіксіз (нақты емес комплексті) функциялар кез-келген
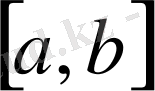 кесіндісінде
кесіндісінде
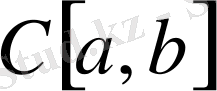 сызықты кеңістігін құрайды. Бұл кеңістіктің функционалдық анализде алатын орны ерекше.
Мысал 3.
сызықты кеңістігін құрайды. Бұл кеңістіктің функционалдық анализде алатын орны ерекше.
Мысал 3.
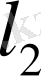 кеңістігі сызықты кеңістік. Себебі, оның элементтері ретінде
кеңістігі сызықты кеңістік. Себебі, оның элементтері ретінде
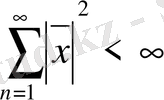
 Equation. 3 шартын қанағаттандыратын сандар (нақты емес комплексті) тізбегі
Equation. 3 шартын қанағаттандыратын сандар (нақты емес комплексті) тізбегі
 алынады, ол сандар үшін
алынады, ол сандар үшін
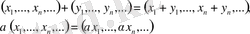 амалдары орындалады.
амалдары орындалады.
 Equation. 3 шартын қанағаттандыратын екі сандар тізбегі үшін осы шарттың орын алатындығы мына
Equation. 3 шартын қанағаттандыратын екі сандар тізбегі үшін осы шарттың орын алатындығы мына
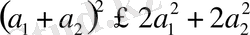 элементар теңсіздіктен шығады.
элементар теңсіздіктен шығады.
1. 2. Нормаланған кеңістік
Нормаланған кеңістіктің анықтамасы
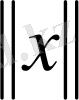
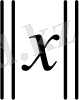
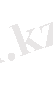 Е -сызықты кеңістік нормаланған кеістік деп аталады, егер әрбір х
Е -сызықты кеңістік нормаланған кеістік деп аталады, егер әрбір х
 Е үшін теріс емес
Е үшін теріс емес
 саны сәйкестендірілсе, және 3 аксиома орындалса.
саны сәйкестендірілсе, және 3 аксиома орындалса.
1) -аксиома норманың азғындалмау шарты, 2) -аксиома норманың біртектілік шарты, 3) - аксиома үшбұрыш теңсіздігі деп аталады. Векторлар жағдайында үш аксиома үшбұрыштың бірқабырғасының ұзындығы қалған екі қабырғасының ұзындықтарының қосындысынан аспайды. Бұдан алатынымыз, үшбұрыштың кез келген қабырғасының ұзындығы қалған екі қабырғасының ұзындықтарының айырмасынан үлкен немесе тең. Норма үшін сәйкес теңсіздік мына түрге келеді:

Бұл теңсіздікті дәлелдейміз. Үшбұрыш теңсіздігі бойынша:
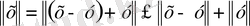
аламыз. Бұдан
; х пен у- тің орнын ауыстырып, алатынымыз:
Соңғы екі теңсіздік (1) - теңсіздікті береді.
Нормаланған кеңістікте кез-келген екі элементтің арақашықтығы төмендегі формуламен анықтауымызға болады.
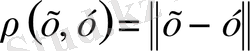
1-жаттығу.
арақашықтығы төмендегі үш шартты қанағаттандыратынын көрсетейік:
 )
)
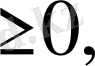
 болғанда ғана
болғанда ғана
 = 0 (тепе -теңдік аксиомасы)
= 0 (тепе -теңдік аксиомасы)
 )
)
 =
=
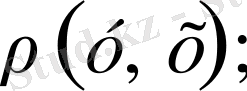 (симметрия аксиомасы)
(симметрия аксиомасы)
)
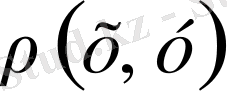

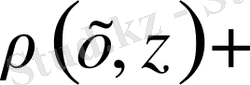
(үшбұрыш аксиомасы)
Анықтама 2.
Х жиыны метрикалық кеңістікдеп аталады, егер әрбір х пен у пар элементеріне
 ,
,
 ,
,
 шарттарын қанағаттандыратын теріс
шарттарын қанағаттандыратын теріс
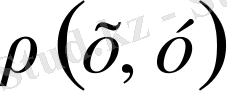 нақты саны сәйкестендірілсе. Бұл жағдайда метрикалық кеңістікті нормаланған кеңістіктің жалпылануы деп санауымызға болады.
нақты саны сәйкестендірілсе. Бұл жағдайда метрикалық кеңістікті нормаланған кеңістіктің жалпылануы деп санауымызға болады.
Е нормаланған кеңістігінде
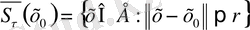 , мұндағы
, мұндағы
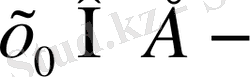 белгіленген нүктесі, ал r
белгіленген нүктесі, ал r
 .
.
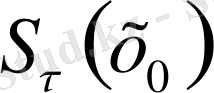 жиыны - центрі
жиыны - центрі
 нүктесі, радиусы r - ге тең ашық шар деп аталады. Бұдан
нүктесі, радиусы r - ге тең ашық шар деп аталады. Бұдан
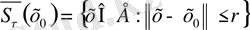 - тұйық шар деп аталады.
- тұйық шар деп аталады.
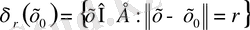 жиыны - сфера деп аталады. Бұдан
жиыны - сфера деп аталады. Бұдан
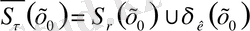 .
.
1-мысал.
Сызықты кеңістікте m- өлшемді R
 бағандары үшін норманы береміз:
бағандары үшін норманы береміз:
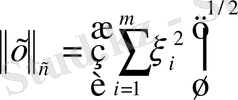
- және 2) норма аксиомалары тривиальді орындалады. Алынған нормаланған кеңістік сызықты алгебрада Е- евклид кеңістігін береді.
2-жаттығу.
m=1, 2, 3 болғанда
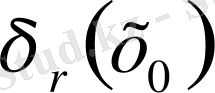 - дің Е
- дің Е
 кеңістігіндегі бейнесі қандай?
кеңістігіндегі бейнесі қандай?
2-мысал. с
 кеңістігі. R
кеңістігі. R
 кеңістігінде норманы мына түрде береміз:
кеңістігінде норманы мына түрде береміз:
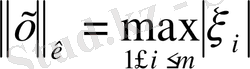
Норма аксиомасын тексереміз.
1)
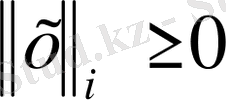 орындалады.
орындалады.
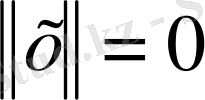 болсын, яғни
болсын, яғни
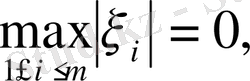 онда барлық
онда барлық
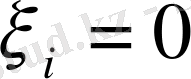 және х=
және х=
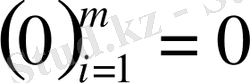
2)
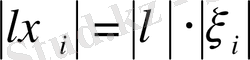 , бұдан норманың біртектілігі шығады.
, бұдан норманың біртектілігі шығады.
3)
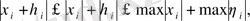 яғни
яғни
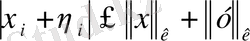 . Теңдіктің сол жағынан үшбұрыш теңсіздігін аламыз.
. Теңдіктің сол жағынан үшбұрыш теңсіздігін аламыз.
3- жаттығу. m=1, 2, 3 болғанда
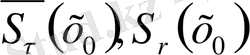
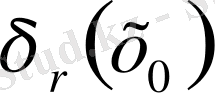 - дің с
- дің с
 кеңістігіндегі бейнесі қандай?
кеңістігіндегі бейнесі қандай?
Ескерту.
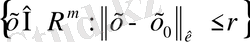 жиыны - қарапайым m-өлшемді куб деп аталады. Бұл түсінік
жиыны - қарапайым m-өлшемді куб деп аталады. Бұл түсінік
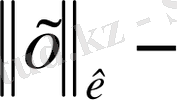 кубтық норма екенін білдіреді.
кубтық норма екенін білдіреді.
 жиыны m-өлшемді шар деп аталады. (
жиыны m-өлшемді шар деп аталады. (
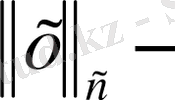 сфералық норма. )
сфералық норма. )
Тізбектің шегі.
Е нормаланған кеңістігінде
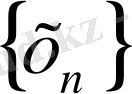 элементтер тізбегін қарастырайық.
элементтер тізбегін қарастырайық.
Анықтама1
. х

 элементін
элементін
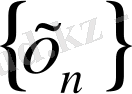 тізбегінің шегі болса, онда оны мына түрде жазамыз.
тізбегінің шегі болса, онда оны мына түрде жазамыз.

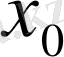 =
=
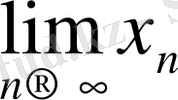 немесе
немесе
 , және
, және
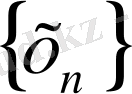 тізбегі
тізбегі
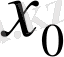 -ге жинақталады деп атаймыз.
-ге жинақталады деп атаймыз.
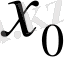 нүктесінің аймағы деп кез келген
нүктесінің аймағы деп кез келген
 ашық шарын айтамыз.
ашық шарын айтамыз.
1-жаттығу.
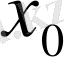 =
=
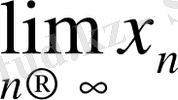 болса, онда
болса, онда
- тізбегінің барлық мүшелерінүктесінің кез келген аймағында кездесетінін
- шегінің жалғыздығын
- тізбегінің кез келген тізбекшесі-ге жинақталатынын
- Егерболса, ондаболатынын
- Егер(болса, ондаболатынын көрсетініз.
- - теңсіздікті қолданып, егер, болса, онда
болатынын дәлелдеу.
Анықтама 2 . Барлық жинақталатын тізбек шенелген екенін дәлелдеңіз.
1-мысал.
с
 - кеңістігін қарастырайық. Осы кеңістікте жинақтылық қандай болады?
- кеңістігін қарастырайық. Осы кеңістікте жинақтылық қандай болады?
Айталық
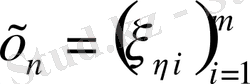 және
және
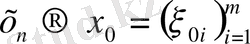 болсын. Онда
болсын. Онда
 ; яғни
; яғни
 . Бұдан
. Бұдан
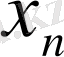 векторының әрбір координатасы сәйкес
векторының әрбір координатасы сәйкес
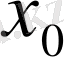 векторының координатасына жинақталады.
векторының координатасына жинақталады.
2-мысал. Е
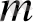 - кеңістігін қарастырайық.
- кеңістігін қарастырайық.
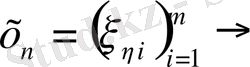
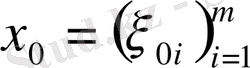
 болсын. Бұл n
болсын. Бұл n

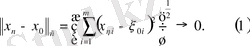 болатынын көрсетеді.
болатынын көрсетеді.
Кез келген
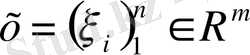 үшін
үшін
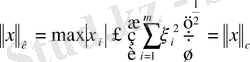 екені белгілі
екені белгілі
болса, онда (1) -ден
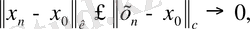
 болатынын көреміз.
болатынын көреміз.
Алдыңғы мысалға келісе отырып, Е
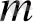 кеңістігінде жинақтылық -- координаталық екенін байқаймыз.
кеңістігінде жинақтылық -- координаталық екенін байқаймыз.
Қосынды үшін берілген Гельдер және Минковский теңсіздігі.
Бұл пункте біз екі басты көмекші теңсіздікті дәлелдейміз.
Айталық p
 және q
және q
 саны
саны
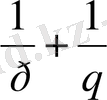 =1 қатынасымен байланысты.
=1 қатынасымен байланысты.
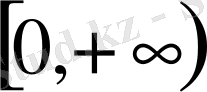 жарты осінде
жарты осінде
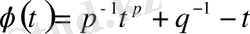 функциясын қарастырайық.
функциясын қарастырайық.
Жаттығу. Дифференциялды есептеу көмегімен
 жарты осінде
жарты осінде
 функциясының жалғыз t=1 минимум нүктесі болатынын дәлелдеңіз.
функциясының жалғыз t=1 минимум нүктесі болатынын дәлелдеңіз.
Бұдан
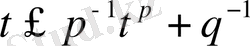 (1) теңсіздігі орынды екені шығады.
(1) теңсіздігі орынды екені шығады.
- - теңсіздікке t=uмәнін қойып, келесі теңсіздікті аламыз:
. (2)
- теңсіздіктен біз қосынды үшін Гельдер теңсіздігін дәлелдейміз.
Кез келген
 және
және
 комплекс саны үшін төмендегі Гельдер теңсіздігі орынды:
комплекс саны үшін төмендегі Гельдер теңсіздігі орынды:
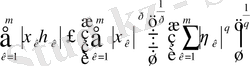 (3)
(3)
Дәлелдеу үшін
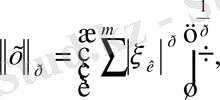
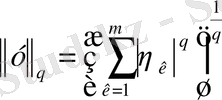 түсінігін енгіземіз. Осы екі теңсіздік нөлден өзгеше болсын делік.
түсінігін енгіземіз. Осы екі теңсіздік нөлден өзгеше болсын делік.
(2) - теңсіздікті қолдана отырып,
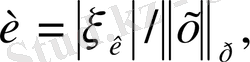
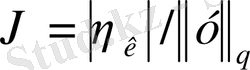 төмендегі теңсіздікті аламыз:
төмендегі теңсіздікті аламыз:
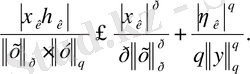
к =1 ден m- ге дейін қосынды құрып, мынаны аламыз:
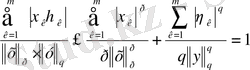
Ары қарай Гельдер теңсіздігі шығады.
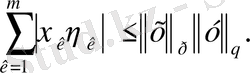
Енді Минковский теңсіздігін дәлелдейміз
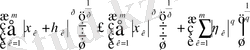 (4)
(4)
Алдымен
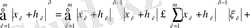
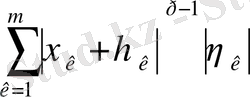 теңсіздігінің оң жағындағы әрбір қосындыға Гельдер теңсіздігін қолданамыз:
теңсіздігінің оң жағындағы әрбір қосындыға Гельдер теңсіздігін қолданамыз:
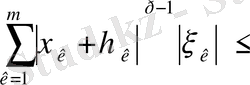
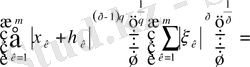
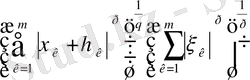
 Тура осылай
Тура осылай
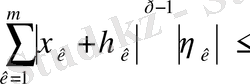
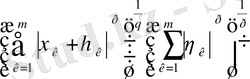 .
.
Соңғы екі теңсіздіктерді біріктіріп, мына теңсіздікті аламыз:
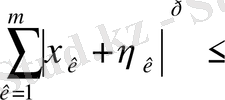
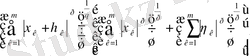 (5)
(5)
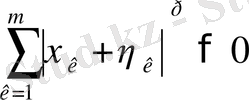 (егер осы қосынды нөлге тең болса, онда Минковский теңсіздігі орынды) деп есептейміз.
(егер осы қосынды нөлге тең болса, онда Минковский теңсіздігі орынды) деп есептейміз.
(5) -ші теңсіздікті
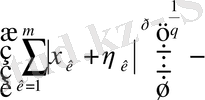 ға бөліп,
ға бөліп,
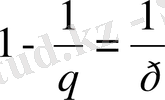 екенін ескере отырып, ізделінді (4) -ті аламыз.
екенін ескере отырып, ізделінді (4) -ті аламыз.
 - кеңістігі
. Айталық
- кеңістігі
. Айталық
 болсын.
болсын.
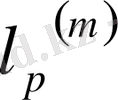 -ді анықтау үшін
-ді анықтау үшін
 - ді нормаланған кеңістікке айналдырамыз:
- ді нормаланған кеңістікке айналдырамыз:

1) және 2) аксиомалары үшін норма белгілі. Үшбұрыш аксиомасы дәлелденген
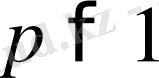 болғандағы Минковский теңсіздігін көрсетеді.
1-жаттығу
.
болғандағы Минковский теңсіздігін көрсетеді.
1-жаттығу
.
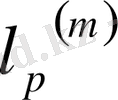 кеңістігіндегі үшбұрыш теңсіздігін дәлелдеңіз.
кеңістігіндегі үшбұрыш теңсіздігін дәлелдеңіз.
 болғанда,
болғанда,
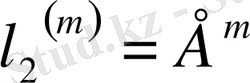 болатынын байқаймыз, яғни
болатынын байқаймыз, яғни
 - евклид кеңістігі.
- евклид кеңістігі.
 - де жинақтылық қандай? Айталық
- де жинақтылық қандай? Айталық
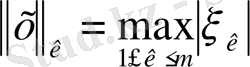 - кубтық норма болсын.
2-жаттығу
. Келесі теңсіздікті дәлелдеңіз:
- кубтық норма болсын.
2-жаттығу
. Келесі теңсіздікті дәлелдеңіз:
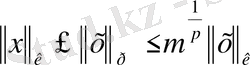
Теңсіздіктің оң жағынан, егер
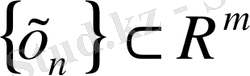 және егер
және егер
 кеңістігінде
кеңістігінде
 болса, онда
болса, онда

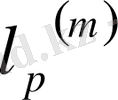 - кеңістігінде
- кеңістігінде
 немесе
немесе
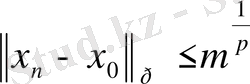
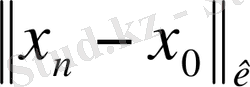 Осы жолмен
Осы жолмен
 және
және
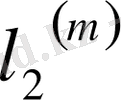 кеңістіктіктеріндегі тізбек жинақтылығы
кеңістіктіктеріндегі тізбек жинақтылығы
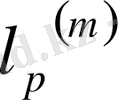 және
және
 -дегі жинақтылыққа сәйкес келеді.
Шектелген m сандық тізбектер кеңістігі
.
-дегі жинақтылыққа сәйкес келеді.
Шектелген m сандық тізбектер кеңістігі
.
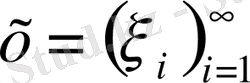 - тізбектер жиынын
- тізбектер жиынын
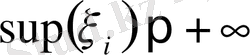 болған жағдайда қарастырайық. Бұл жиын m-әріпімен белгіленеді. Егер
болған жағдайда қарастырайық. Бұл жиын m-әріпімен белгіленеді. Егер
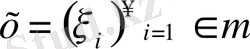 және
және
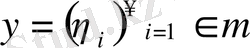 болса, онда анықтама бойынша
болса, онда анықтама бойынша
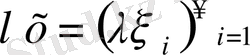 ,
,
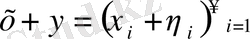 .
.
Жаттығу
. Егер
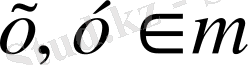 болса, онда
болса, онда
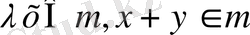 екенін дәлелдеңіз
екенін дәлелдеңіз
(мұндағы m-сызықты кеңістік)
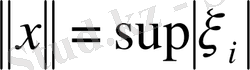 екенін ескеріп, m- ді нормаланған кеңістікке айналдырамыз.
екенін ескеріп, m- ді нормаланған кеңістікке айналдырамыз.
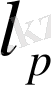 ,
,
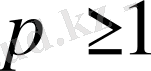 кеңістігі.
Барлық сандық тізбек
кеңістігі.
Барлық сандық тізбек
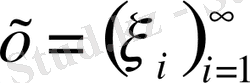 үшін
үшін
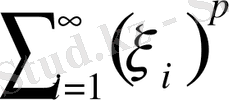 қатары жинақталатын
қатары жинақталатын
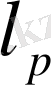 жиынын қарастырамыз.
жиынын қарастырамыз.
1-жаттығу
. Егер
 болса, онда
болса, онда
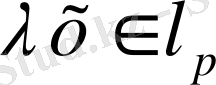 болатынын көрсетіңіз.
болатынын көрсетіңіз.
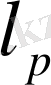 -
да норманы мына формула арқылы бойынша көрсетеміз:
-
да норманы мына формула арқылы бойынша көрсетеміз:
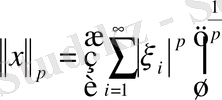 .
.
2-жаттығу. Норманың 1) және 2) аксиомасын тексеріңіз.
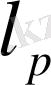 -
кеңістігінде үшбұрыш теңсіздігін дәлелдейміз. (4) -ші соңғы қосынды үшін Минковский теңсіздігінің оң жағын көбейтіп, m- ді
-
кеңістігінде үшбұрыш теңсіздігін дәлелдейміз. (4) -ші соңғы қосынды үшін Минковский теңсіздігінің оң жағын көбейтіп, m- ді
 -
ге ауыстырып, алынған теңсіздіктен
-
ге ауыстырып, алынған теңсіздіктен
 ,
,
 ұмтылдырамыз. Содан
ұмтылдырамыз. Содан
 үшін төмендегі теңсіздікті аламыз:
үшін төмендегі теңсіздікті аламыз:
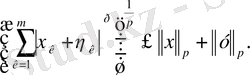
Бұл жерде
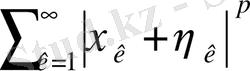 қатары жинақталады және мына теңсіздік орынды:
қатары жинақталады және мына теңсіздік орынды:
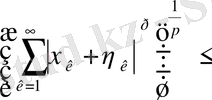
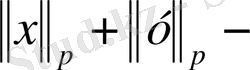 бұл үщбұрыш теңсіздігі, яғни
бұл үщбұрыш теңсіздігі, яғни
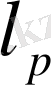 -
нормаланған кеңістік.
-
нормаланған кеңістік.
С[a, b] үзіліссіз функциялар кеңістігі.
[а, b] кесіндісіндегі барлық үзіліссіз функциялардың сызықты кеңістігін қарастырамыз. Норманы мына түрде береміз:
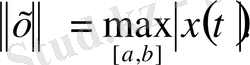
1) және 2) аксиома орындалады. 3) аксиоманы тексерейік. Модульдің қасиеті бойынша
 үшін
үшін
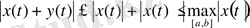
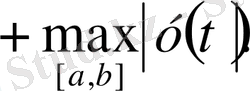 аламыз. Бұдан
аламыз. Бұдан
 болады. Егер
болады. Егер
 - ны сол жағынан алатын болсақ, теңсіздік сақталады. Нәтижесінде С[a, b] нормасы үшін үшбұрыш теңсіздігін аламыз.
- ны сол жағынан алатын болсақ, теңсіздік сақталады. Нәтижесінде С[a, b] нормасы үшін үшбұрыш теңсіздігін аламыз.
Енді С[a, b] -да нормасы бойынша бірқалыпты жинақтылықтың бар екенін көрсетейік.
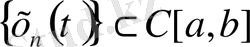 тізбегі берілсін делік және ол
тізбегі берілсін делік және ол
 ға жинақталады, яғни
ға жинақталады, яғни
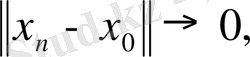
 . Бұл
. Бұл
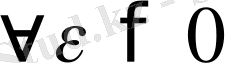 саны үшін
саны үшін
 номері табылатынын және
номері табылатынын және
 саны үшін
саны үшін
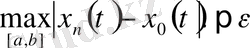 теңсіздігі орынды екенін білдіреді. Сонымен қатар
теңсіздігі орынды екенін білдіреді. Сонымен қатар
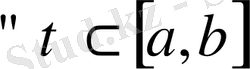 үшін
үшін
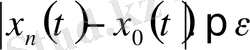 орындалады, яғни норма бойынша С[a, b] -да жинақтылық - бірқалыпты.
орындалады, яғни норма бойынша С[a, b] -да жинақтылық - бірқалыпты.
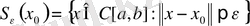 аймағы С[a, b] кеңістігінде қалай берілетінін көреміз. Бұл үшін
аймағы С[a, b] кеңістігінде қалай берілетінін көреміз. Бұл үшін
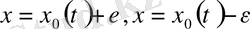 функцияларының графигін тұрғызамыз. Осы екі график және t=a, t=b түзулерінің аралығы
функцияларының графигін тұрғызамыз. Осы екі график және t=a, t=b түзулерінің аралығы
 жолағын шектейді және
жолағын шектейді және
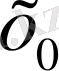 нүктесінің
нүктесінің
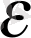 аймағы болып табылады.
аймағы болып табылады.
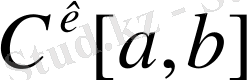 -кеңістігі.
Сызықты кеңістікте [a, b] - да
-кеңістігі.
Сызықты кеңістікте [a, b] - да
 ретті үзіліссіз дифференциалданатын функциялардың нормасын төмендегідей аламыз:
ретті үзіліссіз дифференциалданатын функциялардың нормасын төмендегідей аламыз:
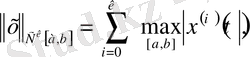 мұндағы
мұндағы

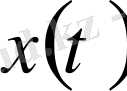 функциясының туындысы.
функциясының туындысы.
Жаттығу.
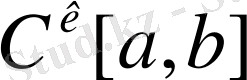 кеңістігінде норма аксиомасын тексеріңіз.
кеңістігінде норма аксиомасын тексеріңіз.
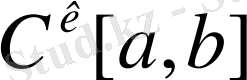 -
дегі жинақтылық --
-
дегі жинақтылық --
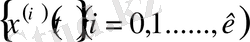 тізбегінің
тізбегінің
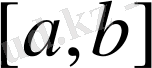 -
ға бірқалыпты жинақталатынын көрсетіңіз.
-
ға бірқалыпты жинақталатынын көрсетіңіз.
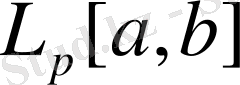 -кеңістігі.
-кеңістігі.
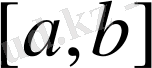 -
де үзіліссіз функциялардың сызықты кеңістігінеқайта оралайық. Норма бұл жағдайда мына түрде болады:
-
де үзіліссіз функциялардың сызықты кеңістігінеқайта оралайық. Норма бұл жағдайда мына түрде болады:
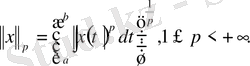
1-жаттығу . 1) және 2) норма аксиомасын тексеріңіз. Үшбұрыш аксиомасы интегралға арналған Минковский теңсіздігін береді:

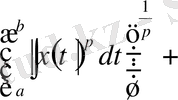
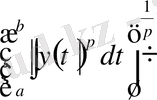 (1)
(1)
Минковский теңсіздігінің дәлелдеуі (
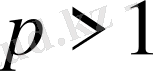 болғанда) Гельдер теңсіздігінен шығады.
болғанда) Гельдер теңсіздігінен шығады.
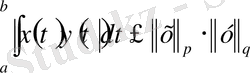 (2)
(2)
мұндағы
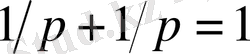 . Егер
. Егер
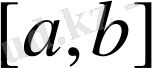 -
да
-
да
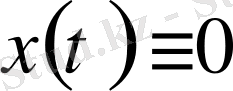 немесе
немесе
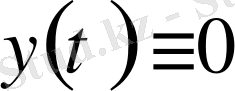 болса (2) -теңсіздік орындалады. Айталық
болса (2) -теңсіздік орындалады. Айталық
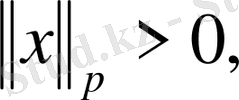
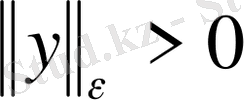 болсын.
болсын.
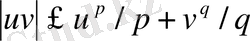 теңсіздігіне
теңсіздігіне
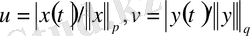 қоямыз. Алынған теңсіздікті интегралдау арқылы мынаны аламыз:
қоямыз. Алынған теңсіздікті интегралдау арқылы мынаны аламыз:
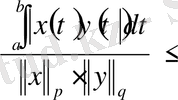

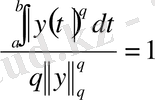
Бұл ізделінді (2) -ші теңсіздікті береді.
Ары қарай қосынды жағдайында мынаны аламыз:
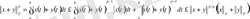
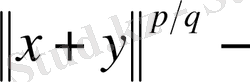 ге қысқартып, (1) -ші Минковский теңсіздігін аламыз.
ге қысқартып, (1) -ші Минковский теңсіздігін аламыз.
Анықтама 1
. Айталық Е - сызықты кеңістігінде екі
 және
және
 нормасы берілсін делік. Егер
нормасы берілсін делік. Егер
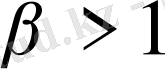 тұрақтысы бар болса, яғни
тұрақтысы бар болса, яғни
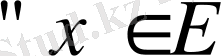 үшін
үшін
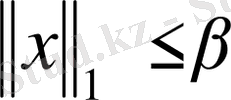
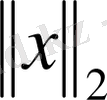 теңсіздігі орындалса,
теңсіздігі орындалса,
 нормасы
нормасы
 нормасына тәуелді дейміз.
нормасына тәуелді дейміз.
2-жаттығу
. Егер сызықты кеңістікте
 және
және
 нормасы берілсе, онда
нормасы берілсе, онда
 тізбегінің жинақтылығынан
тізбегінің жинақтылығынан
 мағынасында оның
мағынасында оның
 мағынасындағы жинақтылығы шығады.
мағынасындағы жинақтылығы шығады.
Ашық және тұйық жиын. Айталық Е- нормаланған кеңістік болсын.
Анықтама1.
 жиыны ашық деп аталады, егер ол өзінің әрбір нүктесінің аймағынан тұратын болса. Онда
жиыны ашық деп аталады, егер ол өзінің әрбір нүктесінің аймағынан тұратын болса. Онда
 ашық жиын, егер
ашық жиын, егер
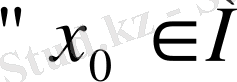 үшін
үшін
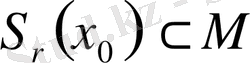 болғанда
болғанда
 саны табылса.
саны табылса.
Айталық Ø жиыны -- анықтама бойынша алынған Е кеңістігіндегі ашық жиын болсын.
Теорема.
 нүктесі
нүктесі
 жиынының шектік нүктесі болуы үшін,
жиынының шектік нүктесі болуы үшін,
 - ға жинақталатын
- ға жинақталатын
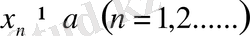 кейбір
кейбір
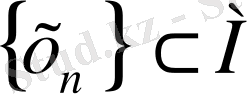 тізбегінің бар болуы қажетті және жеткілікті.
тізбегінің бар болуы қажетті және жеткілікті.
Дәлелдеуі.
Қажеттілігі. Айталық
 -
-
 жиынының шектік нүктесі болсын;
жиынының шектік нүктесі болсын;
 деп таңдап алып, және
деп таңдап алып, және
 табамыз. Содан соң
табамыз. Содан соң
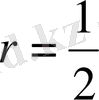 деп алып
деп алып
 табамыз. Осы процесті жалғастыра отырып,
табамыз. Осы процесті жалғастыра отырып,
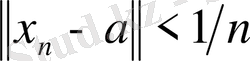 шарты орындалатындай
шарты орындалатындай
 тізбегін табамыз.
тізбегін табамыз.
Жеткіліктілігі.
 нүктесіне жинақталатын
нүктесіне жинақталатын
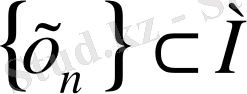 бар болсын. Бұл
бар болсын. Бұл
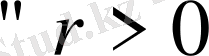 үшін
үшін
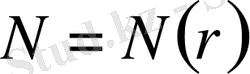 нөмірі табылып,
нөмірі табылып,
 барлық
барлық
 үшін орындалатындығын көрсетеді.
үшін орындалатындығын көрсетеді.
Анықтама 2.
 жиыны тұйық деп аталады, егер ол өзінің шектік нүктелерінен тұрса, Ø бос жиыны әрқашан тұйық жиын болады.
жиыны тұйық деп аталады, егер ол өзінің шектік нүктелерінен тұрса, Ø бос жиыны әрқашан тұйық жиын болады.
Мысал.
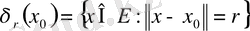 сферасы тұйық жиын. Шынында да,
сферасы тұйық жиын. Шынында да,
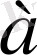 - шектік нүктесі
- шектік нүктесі
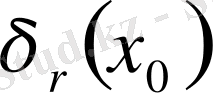 болсын. Демек
болсын. Демек
 табылады. Үшбұрыш теңсіздігі бойынша
табылады. Үшбұрыш теңсіздігі бойынша
 ұмтылғанда
ұмтылғанда
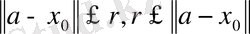 болады.
болады.
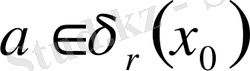 болғандықтан
болғандықтан
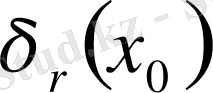 - тұйық болады.
- тұйық болады.
Анықтама 3.
Айталық
 ,
ал
,
ал
 -
-
 шектік нүктелерінің жиыны.
шектік нүктелерінің жиыны.
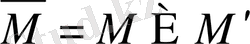 жиыны -
жиыны -
 жиынының тұйықталуы деп аталады.
жиынының тұйықталуы деп аталады.
2-мысал.
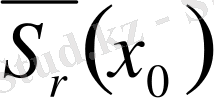 -
-
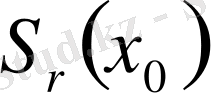 - дің тұйықталуы.
- дің тұйықталуы.
3-жаттығу.
1)
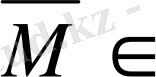
 -
тұйық жиын, 2)
-
тұйық жиын, 2)
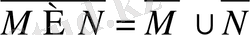 ,
3)
,
3)
 тұйық
тұйық
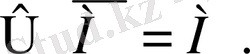
Шекті өлшемді кеңістіктегі норманың эквиваленттілігі.
Анықтама1.
Айталық Е - сызықты кеңістік және Е кеңістігінде екі жағдаймен нормалар берілсін:
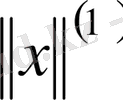 және
және
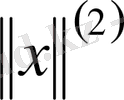 .
.
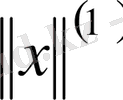 және
және
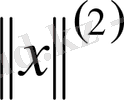 нормалары эквивалентті деп аталады, егер
нормалары эквивалентті деп аталады, егер
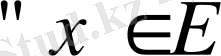 үшін
үшін
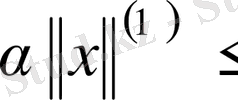
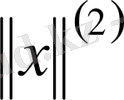

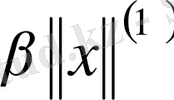 орындалатындай,
орындалатындай,
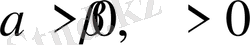 саны табылса.
саны табылса.
Жаттығу. Норманың эквиваленттілік қатынасы келесі қасиеттерге ие:
- ~(рефлексифтілігі)
- егер~болса, онда~( симметриялылығы)
- егер~, ал~болса, онда~. (транзитивтілігі) .
Теорема. Барлық шекті өлшемді сызықты кеңістікте барлық нормалар эквивалентті.
Дәлелдеуі.
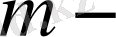 өлшемді Е сызықты кеңістікте
өлшемді Е сызықты кеңістікте
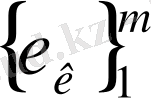 базисін белгілейміз, және
базисін белгілейміз, және
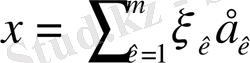 --
осы базис бойынша алынған
--
осы базис бойынша алынған
 жіктелуі.
жіктелуі.
Айталық
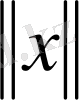 -
Е кеңістігіндегі тағы бір кез- келген норма болсын.
-
Е кеңістігіндегі тағы бір кез- келген норма болсын.
Ары қарай
 -
-
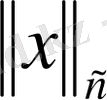 -
ға тәуелді,
-
ға тәуелді,
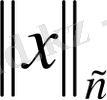 --
--
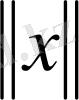 -
қа тәуелді болатынын көрсетейік. Бұл
-
қа тәуелді болатынын көрсетейік. Бұл
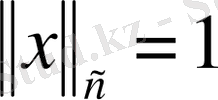 сферасында
сферасында
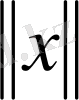 функциясын қарастырайық.
функциясын қарастырайық.
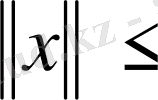
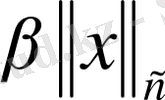 екенін ескеріп мынаны аламыз:
екенін ескеріп мынаны аламыз:
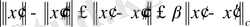 .
Бұдан
.
Бұдан
 функциясының
функциясының
 -дегі үзіліссіздігі шығады. Сонымен қатар
-дегі үзіліссіздігі шығады. Сонымен қатар
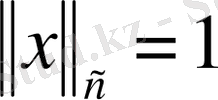 сферасында
сферасында
 тұйық және шектелген жиын болады.
тұйық және шектелген жиын болады.
Келесі теореманы берейік:
Теорема.
 тұйық шектелген жиынындағы үзіліссіз функцияда шектелген болады және
тұйық шектелген жиынындағы үзіліссіз функцияда шектелген болады және
 -де өзінің жоғарғы және төменгі шекараларын қабылдайды.
-де өзінің жоғарғы және төменгі шекараларын қабылдайды.
Осы теоремаға сүйеніп,
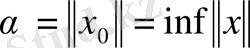 болғанда
болғанда
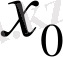 нүктесі табылатынын байқаймыз.
нүктесі табылатынын байқаймыз.
 болғанда немесе
болғанда немесе
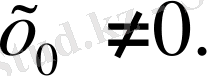 Бұдан
Бұдан
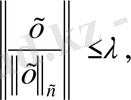
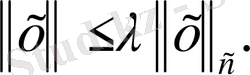 Демек,
Демек,
 ~
~
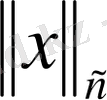 .
.
Нормаланған кеңістіктер кеңістігі. Нүктеден кеңістікке дейінгі арақашықтық.
Анықтама . L - тұйық сызықты көпбейнесі Е - нормаланған кеңістігіндегі ішкі кеңістік деп аталады.
Лемма.
Егер
 болса, онда
болса, онда
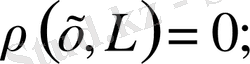 егер де
егер де
 болса, онда
болса, онда
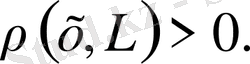
Дәлелдеуі.
Егер
 болса, онда
болса, онда
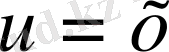 деп қабылдап,
деп қабылдап,
 аламыз. Яғни
аламыз. Яғни
 .
.
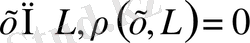 болсын. Онда
болсын. Онда
 анықтамасы бойынша кез келген натурал
анықтамасы бойынша кез келген натурал
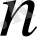 үшін
үшін
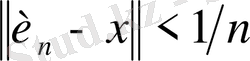 болғанда,
болғанда,
 табылады. Бұл жерде
табылады. Бұл жерде
 .
.
 тұйықталуының зерттелуінде
тұйықталуының зерттелуінде
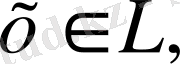 бірақ шарт бойынша
бірақ шарт бойынша
 . Алынған қарама- қайшылық
. Алынған қарама- қайшылық
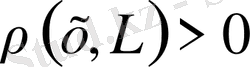 екенін дәлелдейді.
екенін дәлелдейді.
Ішкі кеңістік элементтері арқылы жақындау.
Егер
 болғанда
болғанда
 элементі бар болса, онда
элементі бар болса, онда

 ішкі кеңістігінің
ішкі кеңістігінің
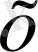 элементтері арқылы жақындаудың ең жақсы элементі деп аталады. Ең жақсы элемент жалғыз болмауы мүмкін, әрі мүлдем болмауы мүмкін.
элементтері арқылы жақындаудың ең жақсы элементі деп аталады. Ең жақсы элемент жалғыз болмауы мүмкін, әрі мүлдем болмауы мүмкін.
 шекті өлшемді болған жағдайда ол элемент бар болады. Шынында да,
шекті өлшемді болған жағдайда ол элемент бар болады. Шынында да,
 болса, онда
болса, онда
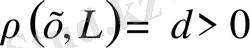 .
.
 кеңістігінде
кеңістігінде
 функциясын қарастырайық. Ол
функциясын қарастырайық. Ол
 кеңістігінде үзіліссіз немесе кез келген
кеңістігінде үзіліссіз немесе кез келген
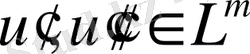 үшін төмендегі теңсіздік орындалады.
үшін төмендегі теңсіздік орындалады.
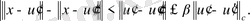
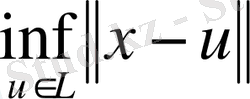 тек шарда орындалатынын көрсетейік.
тек шарда орындалатынын көрсетейік.
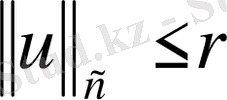 , мұндағы
, мұндағы
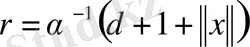 Демек, егер
Демек, егер
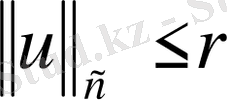 болса, онда
болса, онда
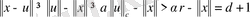
болады, яғни
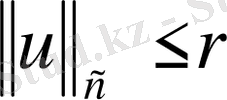 шарының сыртында
шарының сыртында
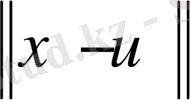 функциясының дәл төменгі шегін қабылдамайды.
функциясының дәл төменгі шегін қабылдамайды.
Теорема.
Айталық
 -
нормаланған
-
нормаланған
 кеңістігінің шекті өлшемді ішкі кеңістігі болсын. Кез келген
кеңістігінің шекті өлшемді ішкі кеңістігі болсын. Кез келген
 үшін
үшін
 бар болады және
бар болады және
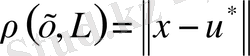 орындалады.
орындалады.
Мысал.
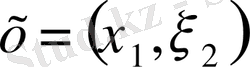 екі өлшемді қатарының
екі өлшемді қатарының
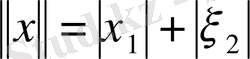 нормасымен берілген
нормасымен берілген
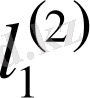 -
кеңістігінен
-
кеңістігінен
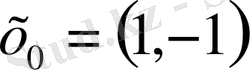 нүктесін және
нүктесін және
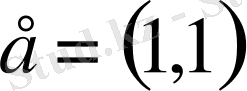 базистік векторымен, (
базистік векторымен, (
 бір өлшемді
бір өлшемді
 ішкі кеңістігін аламыз. Ара қашықтығын анықтайық:
ішкі кеңістігін аламыз. Ара қашықтығын анықтайық:
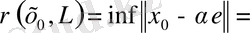
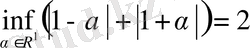 .
.
Зерттей келе,
 элементерінің көмегімен
элементерінің көмегімен
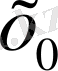 -ге жақындайтын
-ге жақындайтын
 ең жақсы элементтерінің шексіз жиыны бар болатынына көзіміз жетеді.
ең жақсы элементтерінің шексіз жиыны бар болатынына көзіміз жетеді.
Рисс леммасы.
Келесі геометриялық тұжырымды келтірейік. Айталық үшөлшемді евклид кеңістігінде
 жазықтығы берілсін. Ол
жазықтығы берілсін. Ол
 координата басынан өтеді, және
координата басынан өтеді, және
 бірлік ұзындық векторы,
бірлік ұзындық векторы,
 перпендикуляр,
перпендикуляр,
 координата басымен берілген. Онда
координата басымен берілген. Онда
 -
ге тиісті кез келген
-
ге тиісті кез келген
 векторы үшін
векторы үшін
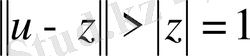 аламыз.
аламыз.
Рисс леммасы
.
Айталық
 -
нормаланған
-
нормаланған
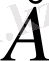 кеңістігіндегі кеңістік,
кеңістігіндегі кеңістік,
 .
Кез келген
.
Кез келген
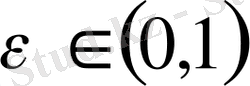 үшін
үшін
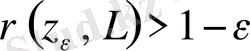 болатындай,
болатындай,
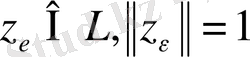 табылады.
табылады.
Дәлелдеуі.
Айталық
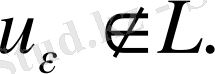
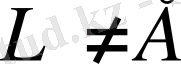 болғандықтан,
болғандықтан,
 бар болады.
бар болады.
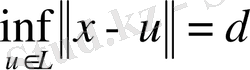 қоямыз,
қоямыз,
 анықтамасын қолданамыз. Кез келген
анықтамасын қолданамыз. Кез келген
 алып, және
алып, және
 орындалатындай
орындалатындай
 табамыз. Енді
табамыз. Енді
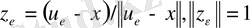 элементін қарастырайық.
элементін қарастырайық.
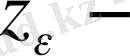 ізделінді элемент екенін ескерейік, шынында да,
ізделінді элемент екенін ескерейік, шынында да,
 .
.
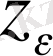 мен
мен
 арасындағы арақашықтық:
арасындағы арақашықтық:
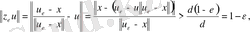 немесе
немесе
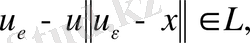 ал
ал
 үшін
үшін
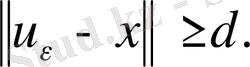
Нормаланған кеңістіктегі тығыз сызықты көпбейне.
Анықтама .
Е нормаланған кеңістігінде жатқан
 - сызықты көпбейнесі Е -де тығыз деп аталады, егер кез келген
- сызықты көпбейнесі Е -де тығыз деп аталады, егер кез келген
 және кез келген
және кез келген
 үшін
үшін
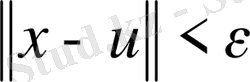
болатындай,
 элементі табылса.
элементі табылса.
Айталық
 -
сызықты кеңістігі Е кеңістігінде тығыз және
-
сызықты кеңістігі Е кеңістігінде тығыз және
 .
.
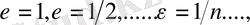 етіп таңдап алып,
етіп таңдап алып,
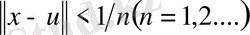 болатындай
болатындай
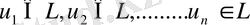 табамыз. Олай болса, егер
табамыз. Олай болса, егер
 сызықты кеңістігі Е кеңістігінде тығыз болса, онда
сызықты кеңістігі Е кеңістігінде тығыз болса, онда
 үшін
үшін
 бар болады, (
бар болады, (
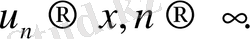 ) .
) .
Орташа және кесілетін функциялар мен олардың кейбір қолданулары.
Анықтама .
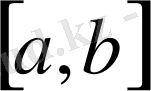 -
да анықталған
-
да анықталған
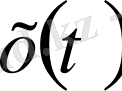 функциясы финитті деп аталады, егер
функциясы финитті деп аталады, егер
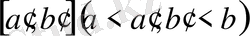 табылса (
табылса (
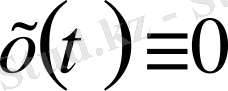 болмағанда) .
болмағанда) .
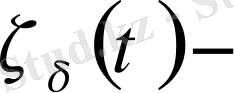 кесілетін функциялары (мұндағы
кесілетін функциялары (мұндағы

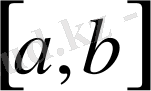 -
да берілген кез келген
-
да берілген кез келген
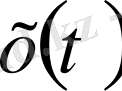 функциясын кесіп алуға мүмкіндік береді:
функциясын кесіп алуға мүмкіндік береді:
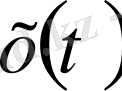
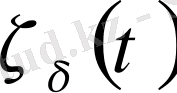 функциясы финитті.
функциясы финитті.
Теорема
1.
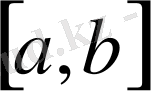 -да үзіліссіз және финитті функциялардың сызықты көпбейнесі
-да үзіліссіз және финитті функциялардың сызықты көпбейнесі
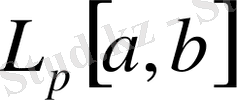 тығыз болады.
тығыз болады.
Дәлелдеуі.
Айталық
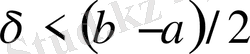 болсын.
болсын.
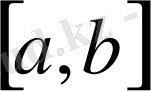 -
да үзіліссіз кез келген
-
да үзіліссіз кез келген
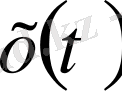 функциялары үшін:
функциялары үшін:
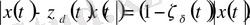
аламыз. Бірақ
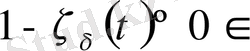
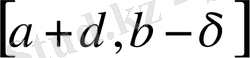 және
және
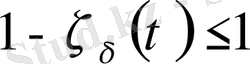 кесіндінің сыртында жатыр, сондықтан
кесіндінің сыртында жатыр, сондықтан
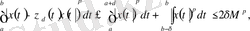 мұндағы
мұндағы
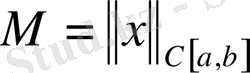 орындалады. Сонымен қатар
орындалады. Сонымен қатар
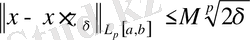 болады.
болады.
Егер
 санын алатын болсақ, онда
санын алатын болсақ, онда
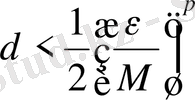 болғанда
болғанда
 финитті функциялары
финитті функциялары
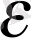 -
нан кіші норма бойынша
-
нан кіші норма бойынша
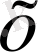 -
тан өзгешеленеді. Теорема дәлелденді.
-
тан өзгешеленеді. Теорема дәлелденді.
Теорема
2.
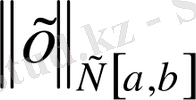 нормасымен берілген
нормасымен берілген
 -да үзіліссіз және финитті функциялардың нормаланған кеңістігінде,
-да үзіліссіз және финитті функциялардың нормаланған кеңістігінде,
 -да финитті, шексіз дифференциалданатын функциялардың сызықты көпбейнесі тығыз болады.
-да финитті, шексіз дифференциалданатын функциялардың сызықты көпбейнесі тығыз болады.
Дәлелдеуі.
Айталық
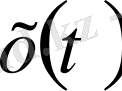
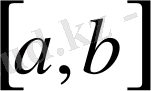 -да үзіліссіз және финитті болсын.
-да үзіліссіз және финитті болсын.
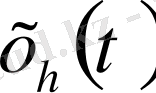 -
орташа функциясын
-
орташа функциясын
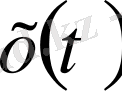 үшін қарастырамыз.
үшін қарастырамыз.
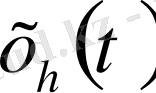 -
-
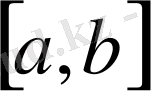 сыртында да шексіз дифференциалданады және
сыртында да шексіз дифференциалданады және
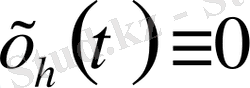 орындалады. Ары қарай,
орындалады. Ары қарай,
 болғанда
болғанда
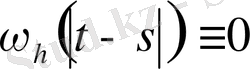 орындалады, ал
орындалады, ал
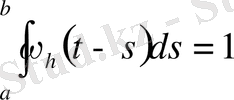 болса, онда төмендегі теңсіздік орындалады:
болса, онда төмендегі теңсіздік орындалады:
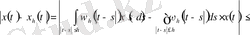
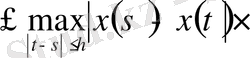
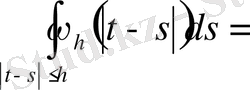
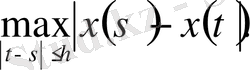
1. 3. Метрикалық кеңістік
Анықтама.
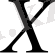 қайыбір бос емес жиын болсын. Егер
қайыбір бос емес жиын болсын. Егер
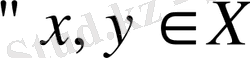 үшін нақты мәнді функция
үшін нақты мәнді функция
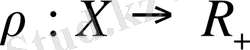 анықталып, келесі шарттарды қанағаттандырса: 1.
анықталып, келесі шарттарды қанағаттандырса: 1.
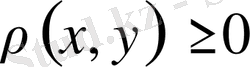 ,
,
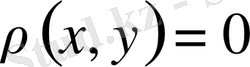

 ; 2.
; 2.
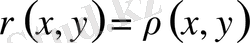 (симметриялық) ; 3.
(симметриялық) ; 3.

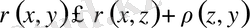 Equation. 3 (үшбұрыш теңсіздігі) ; Онда ол функцияны (функционал)
Equation. 3 (үшбұрыш теңсіздігі) ; Онда ол функцияны (функционал)
 жиынындағы метрика деп аталады.
жиынындағы метрика деп аталады.

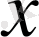 және
және
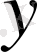 нүктелерінің арасындағы ара қашықтық.
Анықтама.
Бос емес
нүктелерінің арасындағы ара қашықтық.
Анықтама.
Бос емес
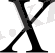 жиыны мен анықталған метрика, яғни
жиыны мен анықталған метрика, яғни
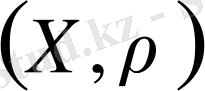 пары метрикалық кеңістік деп аталады. Осы пар,
пары метрикалық кеңістік деп аталады. Осы пар,
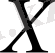 жиыны мен
жиыны мен
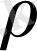 функциясы метрикалық кеңістік жасайды. Оны
функциясы метрикалық кеңістік жасайды. Оны
 немесе
немесе
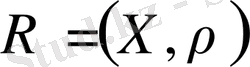 арқылы белгіленеді. Жоғарыда көрсетілген қасиеттер метрикалық кеңістіктің аксиомалары деп аталады. Бір жиында бірнеше метрика анықталса, онда бірнеше метрикалық кеңістік алуға болады.
Мысалы.
1.
арқылы белгіленеді. Жоғарыда көрсетілген қасиеттер метрикалық кеңістіктің аксиомалары деп аталады. Бір жиында бірнеше метрика анықталса, онда бірнеше метрикалық кеңістік алуға болады.
Мысалы.
1.
 (
(
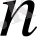 Equation. 3 өлшемді кеңістік) болсын. Егер
Equation. 3 өлшемді кеңістік) болсын. Егер
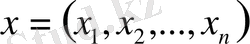 және
және
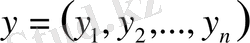 бұл кеңістіктің
бұл кеңістіктің
 екі нүктесі болсын, онда
екі нүктесі болсын, онда
 метрикалық кеңістік келесі өрнекпен
метрикалық кеңістік келесі өрнекпен
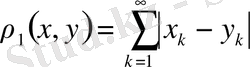 анықтауға болады, себебі
анықтауға болады, себебі
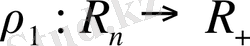 жоғарыдағы қасиеттерді қанағаттандырады. Онда
жоғарыдағы қасиеттерді қанағаттандырады. Онда
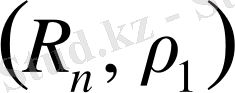 - метрикалық кеңістік болады. 2. Егер
- метрикалық кеңістік болады. 2. Егер
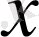 және
және
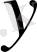 нүктелері берілсе, онда
нүктелері берілсе, онда
 ара қашықтығын
ара қашықтығын
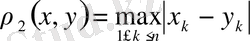 өрнегі бойынша да анықтауға болады. Онда
өрнегі бойынша да анықтауға болады. Онда
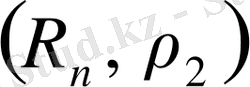 - метрикалық кеңістік болады. 3.
- метрикалық кеңістік болады. 3.
 нақты сандар жиыны болсын, онда
нақты сандар жиыны болсын, онда
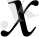 және
және
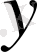 нүктелерінің ара қашықтығын
нүктелерінің ара қашықтығын
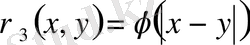 өрнегі арқылы табуға болады. Мұндағы
өрнегі арқылы табуға болады. Мұндағы
 барлық
барлық
 үшін анықталған, екі рет үзіліссіз дифференциалданатын, монмтонды өспелі
үшін анықталған, екі рет үзіліссіз дифференциалданатын, монмтонды өспелі
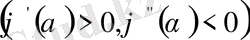 және
және
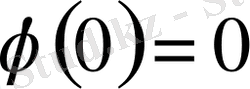 болатын функция. Бастапқы 1, 2 қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
болатын функция. Бастапқы 1, 2 қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
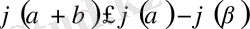 қатынасынан шығады. Сондықтан
қатынасынан шығады. Сондықтан
 метрикалық кеңістік болады. Егер
метрикалық кеңістік болады. Егер
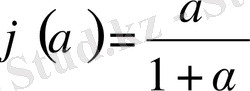
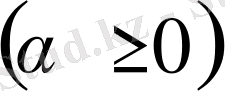 деп алсақ, онда
деп алсақ, онда
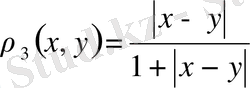 өрнегі де 1, 3 шарттарды қанағаттандырады. Онда
өрнегі де 1, 3 шарттарды қанағаттандырады. Онда
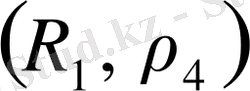 - метрикалық кеңістік болады. Бұл жағдайда
- метрикалық кеңістік болады. Бұл жағдайда
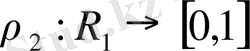 . 4. Комплекс сандар жиынында радиусы бірге тең ашық дөңгелектің
. 4. Комплекс сандар жиынында радиусы бірге тең ашық дөңгелектің
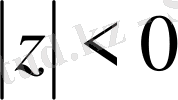
 және
және
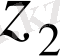 нүктелерінің ара қашықтығын
нүктелерінің ара қашықтығын
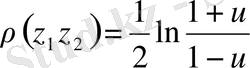
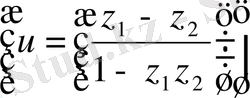 өрненімен анықтауға болады. Метрикалық кеңістіктің аксиомаларының орындалуының себебі, бұл метрикалық кеңістік болғаны. Бұл үш мысалдағы кеңістіктер векторлық кеңістіктер болса, онда соңғы мысалдағы кеңістік сызықты емес кеңістік. 5.
өрненімен анықтауға болады. Метрикалық кеңістіктің аксиомаларының орындалуының себебі, бұл метрикалық кеңістік болғаны. Бұл үш мысалдағы кеңістіктер векторлық кеңістіктер болса, онда соңғы мысалдағы кеңістік сызықты емес кеңістік. 5.
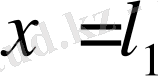 бұл жиынның нүктелері
бұл жиынның нүктелері

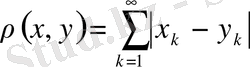 өрнегімен анықтауға болады. Бұл жағдай алғашқы екі қасиет оңай тексерілді, ал үшіншісін келесі түрде тексеруге болады. Егер
өрнегімен анықтауға болады. Бұл жағдай алғашқы екі қасиет оңай тексерілді, ал үшіншісін келесі түрде тексеруге болады. Егер
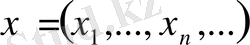 және
және
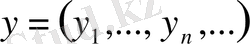
 болса, онда
болса, онда
 үшін
үшін
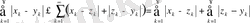 теңсіздігінен шекке көшу арқылы
теңсіздігінен шекке көшу арқылы
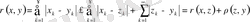 теңсіздігін алуға болады. Онда
теңсіздігін алуға болады. Онда
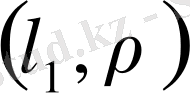 - метрикалық кеңістік. Бұл кеңістікті кейде
- метрикалық кеңістік. Бұл кеңістікті кейде
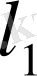 арқылы ғана белгілейміз. 6.
арқылы ғана белгілейміз. 6.
 болсын. Бұл жиынның нүктелері
болсын. Бұл жиынның нүктелері
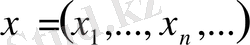
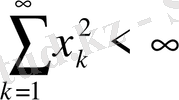 шартты қанағаттандыратын сан тізбегі. Метриканы
шартты қанағаттандыратын сан тізбегі. Метриканы
 өрнегімен анықтауға болады. 7.
өрнегімен анықтауға болады. 7.
 болсын. Бұл жиынның нүтелері
болсын. Бұл жиынның нүтелері
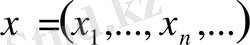 ,
,
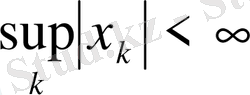 шарттарын қанағаттандыратын сандар тізбегі. Егер
шарттарын қанағаттандыратын сандар тізбегі. Егер
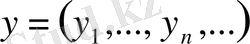 ,
,
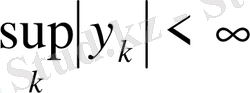 шарттарын қанағаттандыратын кез-келген сандар тізбегі болса, онда метриканы
шарттарын қанағаттандыратын кез-келген сандар тізбегі болса, онда метриканы
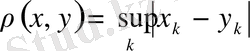 өрнегі бойынша алуға болады, себебі
өрнегі бойынша алуға болады, себебі
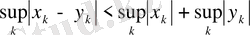 теңсіздігінен оның ұғымы шығады. Метриканың 1, 2 аксиомалары бұл жағдайда оңай тексерілді, ал үшінші аксиомасынан
теңсіздігінен оның ұғымы шығады. Метриканың 1, 2 аксиомалары бұл жағдайда оңай тексерілді, ал үшінші аксиомасынан

теңсіздігінен алуға болады. Сонымен
 - метрикалық кеңістік, ал оны шектеген сан тізбектер кеңістігі деп аталады.
Анықтама.
Егер оның толықтауышы ашық болса, онда метрикалық кеңістік тұйық деп аталады.
Анықтама.
- метрикалық кеңістік, ал оны шектеген сан тізбектер кеңістігі деп аталады.
Анықтама.
Егер оның толықтауышы ашық болса, онда метрикалық кеңістік тұйық деп аталады.
Анықтама.
 және
және
 метрикалық кеңістіктегі жиындар болсын. Егер
метрикалық кеңістіктегі жиындар болсын. Егер
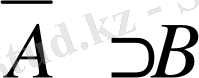 болса, онда
болса, онда
 -да
-да
 жиыны тығыз деп аталады. Егер
жиыны тығыз деп аталады. Егер
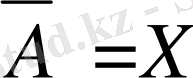 болса, онда
болса, онда
 -та
-та
 жиыны барлық жерде дерлік тығыз деп аталды.
жиыны барлық жерде дерлік тығыз деп аталды.
1. 4. Гильберт кеңістігі
Гильберт кеңістігінің анықтамасы.
Сколяр көбейтінді анықталған кеңістік Гильберт кеңістігі деп аталады.
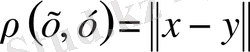 метрикасы мағынасында толық ақырсыз өлшемді унитар кеңістік Гильберт кеңістігі деп аталады да
метрикасы мағынасында толық ақырсыз өлшемді унитар кеңістік Гильберт кеңістігі деп аталады да
 арқылы белгіленеді. Гильберт кеңістігінің ең қарапайым мысалы
арқылы белгіленеді. Гильберт кеңістігінің ең қарапайым мысалы
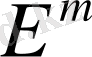 Евклид кеңістігі болып табылады.
Евклид кеңістігі болып табылады.
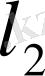 кеңістігінің толық, яғни гильбертті кеңістігі екенін көрсетейік. Фундаментальді
кеңістігінің толық, яғни гильбертті кеңістігі екенін көрсетейік. Фундаментальді
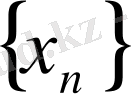 тізбегін
тізбегін
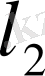 -ден аламыз, мұндағы
-ден аламыз, мұндағы
 .
.
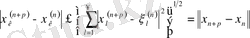 болса, онда әрбір кез келген
болса, онда әрбір кез келген
 сандық
сандық
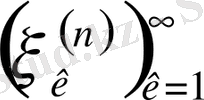 тізбегі
тізбегі
 - кеңістігінде фундаментальді, әрі жинақты болады.
- кеңістігінде фундаментальді, әрі жинақты болады.
Айталық
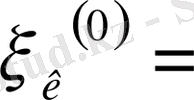
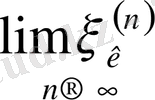 болсын.
болсын.
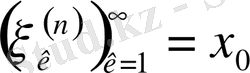 сандық тізбегін қарастырайық және
сандық тізбегін қарастырайық және
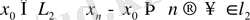 екенін көрсетейік.
екенін көрсетейік.
 фундаментальдығынан барлық
фундаментальдығынан барлық
 үшін
үшін
 нөмірі табылып,
нөмірі табылып,
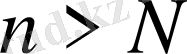 болғанда кез келген натурал
болғанда кез келген натурал
 саны үшін мына теңсіздік орындалады:
саны үшін мына теңсіздік орындалады:
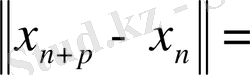
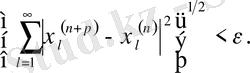
Бірақ онда барлық
 нөмірі үшін:
нөмірі үшін:
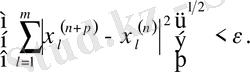
Соңғы теңсіздікте шекке көшсек,
 болғанда барлық
болғанда барлық
 үшін:
үшін:
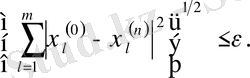 Енді
Енді
 көшемізжәне
көшемізжәне
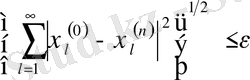 табамыз. Алынған теңсіздік
табамыз. Алынған теңсіздік
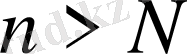 болғанда,
болғанда,
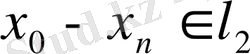 және
және
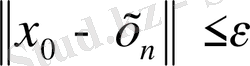 екенін білдіреді. Онда
екенін білдіреді. Онда
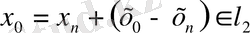 бірақ та
бірақ та
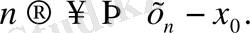
Нүктеден тұйық дөңес кеңістікке дейінгі арақашықтық.
Айталық
 Гильберт кеңістігінде
Гильберт кеңістігінде
 жиыны және
жиыны және
 нүктесі берілсін.
нүктесі берілсін.
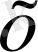 нүктесінен
нүктесінен
 жиынына дейінгі ара қашықтықты
жиынына дейінгі ара қашықтықты
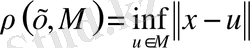 формуласы бойынша анықтаймыз.
формуласы бойынша анықтаймыз.
Лемма.
Егер
 болса, онда
болса, онда
 болады. Егер
болады. Егер
 және
және
 тұйық болса, онда
тұйық болса, онда
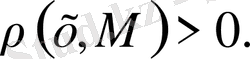
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz