Кеңістіктегі түзу: беру тәсілдері, параметрлік және канондық теңдеулер, жазықтықпен өзара орналасу шарттары

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Түзу берілуінің әр түрлі тәсілдері

d- кеңістіктегі қандай болса да берілген бір тузу болсын, Mо нүктесі осы түзуге тиісті нүкте. L =0 - векторdтүзуіне параллкль вектор (dтүзуінің бағыттаушы векторы),

Сонда М ≡ d ⬄ Mо М және L вғекторлары коллинеар:

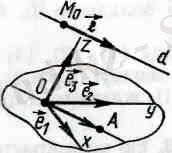
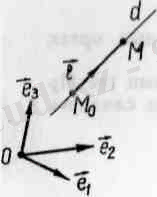
Сөйтіп, d түзуін беру үшін онын, бір М ₀ нүктесін және бағыттаушы L векторын беру жеткілікті. Осылайша М ₀ нүктесімен

және L векторымен берілген түзуін [М ₀ , L ] деп белгілейтін боламыз.

(1) формула d түзудің нүктелерімен және параметр t ≡ R мәндері арасындағы өз ара бір мәнділік сәйкестікті тағайындайды, t параметрі

d түзуінің бойындағы М ≡ d нүктесінің {М ₀ , L } координаталар системасындағы координатасы болып табылады. Кеңістікте қандай да болсын бір аффиндік координаталар системасы R = {0, е ₁ е ₂ , е ₃ } берілсін, осы системаға қатысты М ₀ және М нүктелерінің координаталары: М ₀ (х ₀ , у ₀ , z ₀ ), М (х, у, z) болсын. L векторын {е ₁ , е ₂ , е ₃ } базистің векторлары бойынша жіктейміз:

L=L ₁ е ₁ + L ₂ е ₂ + L ₃ е ₃ .

(1) формуладағы вектордың аттас координаталарымен салыстырып, мынаны аламыз:

Х = Х ₀ +L ₁ t,

у=у ₀ + L ₂ t, (2)

z= z ₀ + L ₃ t.

Керісінше, (2) ⬄ (1) . Сөйтіп, (2) тендеулері кеңістікте d түзуін анықтайды. Бүл тендеулерді түзудің параметрлік тендеулері деп атайды.

2. Егер t-t ₂ -t ₃ ≠ О болса, онда (2) теңдеулерден t-ні шығарып тастап, мынаны аламыз:

x-x ₀ = y - y ₀ = z-z ₀

t t ₂ t ₃

Егер d түзуінің бағыттаушы L векторьшың координаталарының біреуі нольге тең болса, мысалы, L ₃ =0 болса, онда

(2) ⬄ x-x ₀ = y - y ₀ = z-z =0

t t ₂

Бұл жағдайда d түзуі ( х О у) жазықтығына параллель болады

(дербес жағдайда, d=(хОу) . Шынында, ОА=L болсын, онда A= (хОу) .

A = (x ОА) болғандықтан, d//(хОу) .

Ал егер d түзуінің бағыттаушы L векторының екі координатасы нольге тең болса, мысалы t ₂ =t ₃ =0 болса, оңда t ₁ ≠ О және

(2) ⬄ у-у ₀ =0, z-z ₀ =0. (3)

Бұл жағдайда түзу d//(хОу), дербес жағдайда, d=(Ох) болады.

(3), (3'), (3") теңдеулер түзудің канондық теңдеулері деп аталады.

3. Егер d түзуінің әр түрлі екі М ₀ және М ₁ нүктесі берілсе,

онда ол анықталады. М ₀ М ₁ векторы осы түзудің бағыттаушы векторы болады. Егер М ₀ және М ₁ нүктелерінің координаталары М ₀ (х ₀ , у ₀ , z ₀ ), М ₁ (х _х , у _и z _{ ) болса, онда

t=М ₀ М ₁ = (х ₁ -х ₀ ) е ₁ +(у ₁ -у ₀ ) e ₂ +(z ₁ -z ₀ ) е ₃

болады, және d=(М ₀ М ₁ ) түзуінің теңдеуін (2) түрінде жазуға болады:

Х = Х ₀ +(х ₁ -х ₀ ) t,

у=у ₀ + (у ₁ -у ₀ ) t, (2)

z= z ₀ + (z ₁ -z ₀ ) t.

A ₁ B ₁ C ₁ A ₁ B ₁ C ₁

4. d түзуін П ₁ және П ₂ екі жазықтықтың қиылысу сызығы ретінде беруге болады: d=П ₁ П П ₂ . Аффиндік координаталар системасында П ₁ және П ₂ жазықтықтары мына теңдеулермен
анықталатын болсын делік:

П ₁ : А _х х+В ₁ у+С ₁ z+D ₁ =0,

П ₂ : А ₂ х+В ₂ у+С ₂ z+D ₂ =0

және

Ранг A ₁ B ₁ C ₁

A ₂ B ₂ C ₂ =2

П ₁ және П ₂ жазықтықтарының қиылысу шарты) .

(4) теңдеулер системасы d=П ₁ П П ₂ түзуін анықтайды. М ≡ d нүктесінің координаталары х, у _, z (4) тендеулер системасының шешімі болып былады.

Егер х ₀ , у ₀ , z ₀ -(4) системаның қандай да бір шешімі болса, онда бұл система мына теңдеулер темасымен мәндес болады.

А ₁ (х-х ₀ ) +В ₁ (у- _Уо ) +С ₁ ( z-z ₀ ) =0,

А ₂ (х-х ₀ ) +В ₂ (у- _Уо ) +С ₂ ( z-z ₀ ) =0,

Бұл (4') системасының жалпы шешімі мына түрде болады:

B ₁ C ₁

х - х _{0 =} t, B ₁ C ₁

B ₂ C ₂ у-у _{0 =} t,

B ₂ C ₂

B ₁ C ₁

z - z _{0 =} t,

B ₂ C ₂

Бұдан

B ₁ C ₁

х - х _{0 +} t,

B ₂ C ₂

B ₁ C ₁

у-у _{0 +} t,

B ₂ C ₂

B ₁ C ₁

z - z _{0 +} t,

B ₂ C ₂

(5) теңдеулер d- П ₁ П П ₂ түзуінің параметрлік теңдеулері болып табылады, d түзуінің бағыттаушы р векторының (жалпы көбейткіші λ≠О дәлдікпен анықталған) координаталары:

Р= В ₁ С ₁ В ₁ С ₁ А ₁ С ₁

В ₂ С ₂ В ₂ С ₂ А ₂ С ₂

болады. Тік бүрышты координаталар системасында р=[п ₁ , п ₂ ], мұнда

п ₁ = {А ₁ , В ₁ , С ₁ }, п ₂ ={А ₂ , В ₂ , С ₂ }- П ₁ және П ₂ жазыктықтарының сәйкес нормаль векторлары