Арифметикалық және логикалық өрнектер, амалдардың орындалу тәртібі және жиындар мен теңдеулер теориясы


Өрнектер
Өрнектер кейбір мәндерді есептеу ережесін белгілейді. Өрнектер тұрақтылардан, айнымалылардан, функциялардан, амалдарды орындау белгілерінен және жақшалардан тұрады.
Арифметикалық өрнектер
Сандық тұрақтылармен айнымалылармен және стандартты функциялармен кәдімгі арифметикалық амалдарды орындауға болады.
Стандартты мәндердің есептелу ережесін білдіретін символдық жазуды арифметикалық өрнек дейміз. BASIC тілінде арифметикалық өрнектер жалпы қабыланған табиғи пішімге жазылады. Ол сандардан, айнымалылардың және функциялардың аттарынан арифметикалық амалдардың таңбаларынан және жақшалардан тұрады.
Арихметикалық амалдардың таңбаларына мыналар жатады:
- ^ - дәрежеге шығару;
- * - көбейту;
- / - бөлу;
- + -қосу;
- - алу.
Өрнектерді жазуда мына мөмендегі ұсыныстар мен шектеулерді ескеру қажет:
1. Формулалар ешқандай төменгі немесе жоғары таңбаларсыз бір қатарға жазылуы тиіс:
Арихметикалық өрнекті жазудың мысалдары:
Математикалық жазылуы BASIC тілінде жазылуы
5 5
а А
в+5 В+5
3с 3* С
а+в
4+с (А+В) /(4+С)
2 Әсіресе өзіңе-өзің сенімсіздеу жағдайларда орындалтын амалдардың реттілігін көрсету үшін дөңгелек жақшаны пайдалану қажет. Жақша ішіндегілер бірнеще кезекте есептеледі. Егер жақшаға алынған өрнектің өзі жақшаға алынған болса, онда есептеу ішкі жақшадан басталады. Жақшаның ішінде амалдар солдан оңға қарай амалдардың дәрежесіне сәйкес орындалады:
- алдымен функцияның мәні есептеледі;
- одан соң барлық дәрежеге шығару амалдары;
- бұдан кейін көбейту мен бөлу;
- ең соңында қосу және бөлу;
Мысады, BASIC тіліндегі -2+А/В*С+3^2 өрнегі мына -2+А/В*С+3^ 2 математикалық өрнекке баламалы. Оны есептеу алгаритімі мынандай реттілікпен орындалады:
- Х= 32;
- Ү=(А/В) С;
- Z=-2+Ү+Х.
3. Арихметикалық амалдың екі таңбасын екі бірінің жаңына бірін қоюға және көбейгіштердің арасындағы көбейту таңбасын қалдырып кетуге болмайды. Мысалы, мына 8ху/-z математикалық өрнекті BASIC тілінде былай жазылады:8*Х*Ү/(-Z) . типтері бірдей арихметикалық өрнектермен арифметикалық амалдар орындалғана сол типтегі нәтиже алынады. A%+ B% +10% = бүтін сан, С1* D= нақты сан.
4. Бүтін және нақты шамалармен орындалатын амалдар нақты нәтиже береді. Мысалы, А*В%= нақты сан, 5. 4*3% =16. 2
5. mju Бүтін дәрежеге шығару көптеген рет көбейту арқылы орындалады. Мысалы, A^ 3% =A*A* A C^ N%= C*C*… C. N рет
6. Егер дәреженің көрсеткіші нақты сан болса, онда нәтижені есептеу ЕХР және LOG функцияның көмегімен жүзеге асырылады: Х^ Y= EXP (Y*LOG(X) ) . Арихметикалық өрнектерді жазуда кететін қателіктер: 3А+В, 2*-В, SIN +В.
Логикалық өрнектер және операциялар
Кейбір жағдайдарда программада қандай әрекет жасау керектігін таңдау қандайда әрекет жасау керктігін таңдау бір айнымалының мәніне тәуелді болады. Мысалы, квадрат теңдеудің түбірлерін есептеу дискриминантының таңбасына байланысты әр түрлі орындалады.
Екі өрнектің мәнін салыстыру нәтижесіне ақиқат және жалған болатын логикалық өрнек алынады. BASIC праграммалау тілінде логикалық мәндер сан түрінде беріледі; нөлдік мән жалған ретінде ал нөл емес мән ақиқат ретінде қарастырылады. Егер праграмма екі өрнекті салыстыра отырып логикалық мәнді өзі есептеп шығаратын болса, онда- 1 мәні алынады.
BASIC праграммалау тілі алты салыстыру операциясын пайдалынылады. Осы операциялардың кейбіреуіне сәйкес келетін стандартты математикалық символдардың таңбалары стандартты пернетақтада болмағандықтан құрама таңбалар ретінде теріліп жазылады:
Таңба Операция
> үлкен
<> тең емес
>= үлкен немесе тең
<= кіші немесе тең
Мұнда «= » таңбасына ерекше назар аудару керек. Жоғарыда біздер бұл таңба таңба меншіктеу операциясын сипаттайды делік. Ал берілген жағдайда «= » таңбасы - бұл логикалық салыстыру операторы. Траслятор берілген таңбаны қалай пайдалану керек екендігін маңынасына қарай өзі анықтайды.
Логикалық өрнектерде пайдалынылатын операциялар логикалық операциялр деп аталынады. Санды пайдаланғанда нәтижесі де сан болатын арихметикалық операцияға ұқсас логикалық операцияларда логикалық өрнектер пайдалынылады және нәтижеде логикалық өрнектер алынады.
Логикалық операциялар праграммалауда кеңінен тараған және жиі пайдалынылады. Ол бір шарттың өзіне бірнеше талаптарды біріктіуге мүмкіндік береді.
BASIC тілінде праграммалауда қызметші сөздердің көмегімен мына төмендегідей алты логикалық операция жиі беріледі:
- AND-коньюнкция (логикалық көбейту) ;
- OR- дизъюнкция (логикалық қосу) ;
- NOT-логикалық теріске шығару;
- XOR- немесе емес;
- EQV-баламалық (бір мезгілдеақиқатнемесе бір мезгілдежалған) ;
- IMP- импликация (бірнеше ақиқат болғанда мәні жалған, қалған басқа жағдайлардың бәрінде екінші жалған және ақиқат) .
Біз осы келтірілген логикалық операциялардың ішінен ( AND) логикалық көбейтуді; ( OR ) логикалық қосуды және ( NOT) логикалық теріске шығаруды қарастырамыз. Бұл операциялардығ қолданылуы нәтижесін мына төмендегідей кестеден көреміз:
А В А AND В А OR В NOTА
Ақиқат Ақиқат Ақиқат Ақиқат Жалған
Ақиқат жалған Жалған Ақиқат
Жалған Ақиқат Жалған Ақиқат Ақиқат
Жалған Жалған Жалған Жалған
AND операциясы. Кестеде көрініп тұрғандай А AND В өрегі А және В операциялары ақиқат болғанда ақиқат болады. Сіз өзініз суретіңізді бөлмеңіздің қабырғасына іліп қойғыңыз келді дейік. Қағылатын шегені А аргументімен, ал болғаны В мен белгілейік. Оң нәтиже алу үшін ( суретті қабырғаға ілу) сіздің қолыңызда шеге де және балға да болу керек. Егер сіз қолыңызда осы аталған екі нәрсенің біреуі ғана болса, онда сіздің бөлмеңізді әсемдей алмайсыз.
OR операциясы. Жоғарыда келтірілген кестеде егер А және В операндыларының кез келгенін мәні (немесе екеунің мәні де) ақиқат болса, А OR В өрнегінің мәні де ақиқат болатындығы көрінеді. Сіз аштығығыңызды аласыз. Ал егер сізді ешқайсы болмаса, онда сіз аш қаласыз. Мұның теріс нәтиже екендігіне келіспеу қиын.
NOT операциясы. Бұл операция қарастырылған операцияларды ішіндегі ең қарапайымы. Оның әрекеті логикалық өрнектің бастапқы мәнін теріске шығару. Басында ақиқат болса, онда NOT А-ның әрекеті жалған болады. Сіздің қолыңызда жоғары мысалда айтылғандай алмаңыз болсын дейік. Осы алманы жеп қойып сіз жағдайды өзгертесіз, нәтижеде сізде ешнәрсе болмайды, яғни жағдай теріске айналады.
Қатынас амалдары
Қатынас амалдарына мынадай амал түрлерін жатқызуға болады:
- >- үлкен
- <- кіші
- =- тең
- <>- тең емес
- >=- үлкен немесе тең
- <=- кіші немесе тең
Қатынас амалдарымен тек сандарды ғана емес, символдарды, жолдарды, жиымдарды және белгілерді салыстыруға болады.
Амалдарды орындау тәртібі
Алгоритмдік тілдерде (Паскаль, Бейсик, Си т. б. ) арифметикалық амалдардың орындалу тәртібі олардың математикалық орындалу тәртібіне сәйкес келеді, яғни алдымен жақша ішіндегі амалдар, сонан соң көбейту, бөлу, қосу, азайту т. б. амалдар орындалады. Төмендегі кестеде әр түрлі амалдардың орындалу реті көрсетілген.
Амалдардың орындалу тәртібін өзгерту үшін жақшаларды пайдалануға болады. Мысалы 2*5+10 өрнегінде әуелі көбейту емес, қосуды орындау қажет болса, 5 пен 10 санының қосындысын жақшаға алып жазамыз. Сонда өрнектің нәтижесі 20 емес, 30-ға тең болады. 2*(5+10) =30.
§4 Көпмүшеліктер теориясы
- Неміс математигі Г. Кантор ұсынған (1874-97) Көпмүшеліктер теориясы шекті және шексіз заттар жүйесін оқып үйренетін негізгі пән болып табылды. Бұл теорияның объектісі-жиын. Жиындар құрамына енетін заттарсол жиынның элементтерідеп аталады. Жиындар теориясы жиынның элементіне қатысты емес қасиеттерін оқып үйренеді.
а∈А жазуы а элементінің А жиынына тиісті екенін білдіреді немес а элементінің А жиынында жататындығын білдіреді. Жиын идеясында Канторға дейінде еңбектер болды. Жиындарды өзара салыстыру әдісін Кантор ойлап тапты. Оның әдісі бойынша жиындар өзара бір мәнді сәйкестендіру (элементтерін) арқылы жүзеге асырылады.
Егер А және В жиындарының арасында өзара бір мәнді сәйкестік орнатуға болатын болса, онда анықтама бойынша мұндай жиындар тең қуатты жиындар деп аталады. Шекті жиындар үшін олардың тең қуаттылығы екі жиынның элемент санын бірдей екенідігін білдіреді. Тең қуаттылықты теңдікпен шатастыруға болмайды. Жиындар тең деп аталды, егер біріндегі әрбір элемент екіншісінен табылатын болса.
1638 жылы Галилей натурал сандар мен олардың квадраттарының арасында бір мәнді сәйкестік орнатуға болатынын анықтады. Егер бір қатарға натурал сандарды, екінші қатарға олардың квадраттарын жазатын болсақ, онда:
1 2 3 4 5 6 7 8 9
1 4 9 16 алуға болады. Галилей мұны Парадокс түрінде бағалады. Онда натурал сандар қанша болса, олардың квадраттарының саны да сонша. Екінші жағынан квадраттар саны натурал сандар санынан әлдеқайда аз. Бұдан шығатын факті барлық квадраттар натурал сан болып табылады, ал натурал сандардың барлығы квадрат болмайды. Мұны математикада К⊂N деп белгілейді. К- N-ге ішкі жиын болып табылады деген сөз. Мұнда К N жиынының дұрыс бөлігі деп аталады. Галилей мысалынан Кантор төмендегідей шешім қабылдады:
«Кейбір жиындар өзінің дұрыс бөлігімен тең қуатты болуы мүмкін. Бірақ бірде бір шекті жиын мұндай қасиетке ие емес».
Жиындар теориясы сан ұғымына өте қызық толықтырулар жасауға мүмкіндік берді. Шекті жиынның қуаты деп - оның элементтерін нөмірлеуге қолданылатын ең үлкен натурал санды айтамыз. Тең қуатты, шекті жиындардың қуаты да тең болады.
Теорема: Егер M қуаты n болатын шекті жиын болатын болса, онда оның (осы жаңа жиындарының элементі болып саналатын) барлық ішкі жиындарының қуаты 2 n болады.
Мысалы: M жиыны а 1 , а 2 , а 3 , элементтерінен тұрсын. Демек жиынның қуаты 8=2 3 тең.
Бір элементті { а 1 }, { а 2 }, { а 3 }
Екі элементті { а 1 , а 2 , }, { а 1 , а 3 }, {а 2 , а 3 }
Үш элементті { а 1 , а 2 , а 3 }
Бос жиын {}
- Теңдеу
Құрамында әріппен белгіленген белгісізі (айнымалысы) бар теңдік теңдеу деп аталады.
Мысалы,
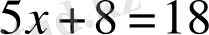 ;
;
 ;
;
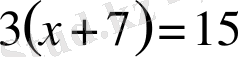 - теңдеулер.
х
- белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе
бір айнымалысы бар теңдеулер
деп атайды.
- теңдеулер.
х
- белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе
бір айнымалысы бар теңдеулер
деп атайды.
Теңдеудің оң жағы және сол жағы болады. Мысалы,
 теңдеуіндегі
теңдеуіндегі
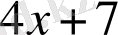 - теңдеудің сол жағы, ал 19-теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады. 4
х
; 7; 19 - мүшелер. Мұндағы 4
х
- белгісізі бар мүше, 7, 19 - бос мүшелер.
- теңдеудің сол жағы, ал 19-теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады. 4
х
; 7; 19 - мүшелер. Мұндағы 4
х
- белгісізі бар мүше, 7, 19 - бос мүшелер.
Теңдеумен берілген мысалдар мен есептерді шығарғанда, ондағы әріппен берілген белгісіздің немесе айнымалының сан мәнін табамыз. Демек, теңдеудің түбірін табамыз.
Белгісіз санның немесе айнымалының теңдеуді тура санды теңдікке айналдыратын мәні теңдеудің түбірі деп аталады.
Теңдеуді шешу дегеніміз - оның түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеу.
Теңдеулерді шешкенде, кейде түбірлері бірдей болатын теңдеулерде кездеседі. Түбірлері бірдей болатын теңдеулерді
мәндес теңдеулер
деп атайды. Мысалы,
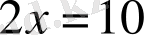 теңдеуі мен
теңдеуі мен
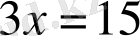 және
және
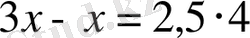 теңдеулері - мәндес теңдеулер. түбірлері бірдей:
теңдеулері - мәндес теңдеулер. түбірлері бірдей:
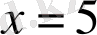 . Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады.
. Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады.
Теңдеу - әрпі бар теңдік болғандықтан, теңдеудің қасиеттерін теңдіктің қасиеттеріне сүйеніп дәлелдейміз.
Теңдеулердің 1-қасиеті.
Теңдеудің екі жағына да бірдей санды немесе әріпті өрнекті қосқанда (азайтқанда) теңдеу мәндес теңдеуге түрленеді.
1-мысал.
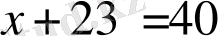
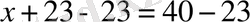
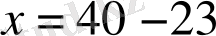
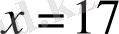 - теңдеудің түбірі.
- теңдеудің түбірі.
Мысалда теңдеулердің бұл қасиетін қолдану нәтижесінде 23 саны теңдеудің сол жағынан қарама-қарсы таңбамен оң жағына көшірілді. Онда теңдеулердің 1-қасиеті бойынша:
теңдеудегі қосылғыштың таңбасын қарама-қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді.
Теңдеуді мұндай түрлендіруді енгізген ІХ ғасырдағы Орта Азия ғалымы Мұхаммед бен Мұса аль-Хорезми. «Алгебра» атауы оның «Китаб аль-джебр валь-мукабала» атты шығармасынан алынған. Теңдеулердің 2-қасиеті:
теңдеудің екі жағында нөлден өзге бірдей санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді.
2-мысал.
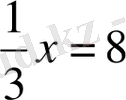 Қысқаша:
Қысқаша:
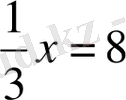
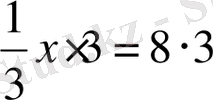
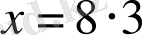
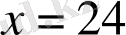
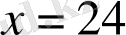
2. Бір айнымалысы бар сызықтық теңдеу және
оның қасиеттері
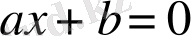 (мұндағы
(мұндағы
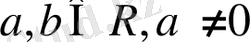 ) түріндегі теңдеу
бір айнымалысы бар сызықтық теңдеу
деп аталады.
) түріндегі теңдеу
бір айнымалысы бар сызықтық теңдеу
деп аталады.
1. Теңдеудің түбірлерін табу: S теңдеудің шешімдер жиыны болсын.
1) Егер
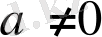 болса,
болса,
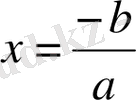 ,
,
2) Егер
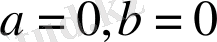 болса, теңдеудің шексіз шешімі
болса, теңдеудің шексіз шешімі
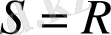 болады.
болады.
3) Егер
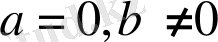 болса, теңдеудің шешімі болмайды
болса, теңдеудің шешімі болмайды
 .
.
2. Теңдеудің қасиеттері:
1)
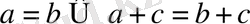
Теңдеудің екі бөлігіне де бірдей санды қосуға болады.
2)
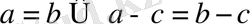
Теңдеудің екі бөлігінен бірдей санды азайтуға болады.
3)
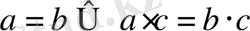
Теңдеудің екі бөлігінен бірдей санға көбейтуге болады.
4)
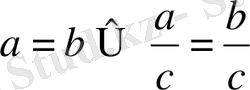
Теңдеудің екі бөлігін нольден өзгеше санға бөлуге болады.
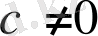
5)
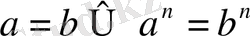
Теңдеудің екі бөлігін бірдей дәреже шығаруға болады.
6)
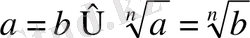
7)
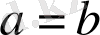 және
және
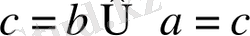
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz