Фурье қатары мен түрлендіруі: анықтамалар, жинақтылығы, қасиеттері және жылу теңдеуін шешу


ФУРЬЕ ТҮРЛЕНДІРУІ
3. 1. Функцияның нүктедегі
біржақты шектері және негізгі ұғымдар
Осы тақырыпта математикалық анализ курсында ([14, 16] ) қарастырылған үзілісті нүктелерге және алдағы тақырыптарда қажетті негізгі ұғымдарға қысқаша тоқталып өтейік.
Мына шектер бар болсын:
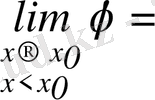
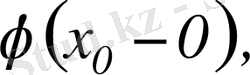
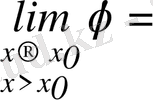
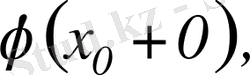
әрі олар сәйкес
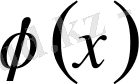 функцияның
функцияның
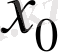 нүктедегі
сол жақты
және
оң жақты шектері
деп аталады. Егер
нүктедегі
сол жақты
және
оң жақты шектері
деп аталады. Егер
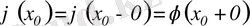 теңдігі орындалса, онда
теңдігі орындалса, онда
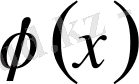 функция
функция
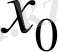 нүктеде үзіліссіз
деп аталады.
нүктеде үзіліссіз
деп аталады.
Егер
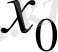 нүктеде
нүктеде
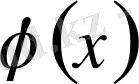 функцияның оң жақты, сол жақты шектерінің бірі немесе екеуіде жоқ болса, онда
функцияның оң жақты, сол жақты шектерінің бірі немесе екеуіде жоқ болса, онда
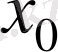 нүкте
екінші түрдегі
үзілісті нүкте
деп аталады. Егер
нүкте
екінші түрдегі
үзілісті нүкте
деп аталады. Егер
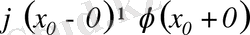 болса, онда
болса, онда
 нүкте
бірінші түрдегі үзілісті нүкте
деп аталады. Егер
нүкте
бірінші түрдегі үзілісті нүкте
деп аталады. Егер
 нүктеде функцияның оң жақты және сол жақты шектер бар болса, онда
нүктеде функцияның оң жақты және сол жақты шектер бар болса, онда
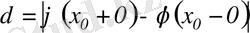 саны
саны
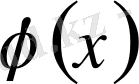 функцияның
функцияның
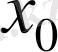 нүктедегі
күрт үзілісті ара қашықтығы
деп аталады.
нүктедегі
күрт үзілісті ара қашықтығы
деп аталады.
Енді
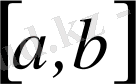 сегментте анықталған
сегментте анықталған
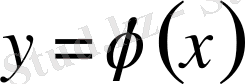 функцияны қарастырайық. Егер
функцияны қарастырайық. Егер
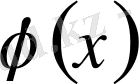 функцияның
функцияның
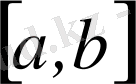 сегментте үзіліссіз туындысы бар болса, онда ол осы сегментте
тегіс
деп аталады. Егер
сегментте үзіліссіз туындысы бар болса, онда ол осы сегментте
тегіс
деп аталады. Егер
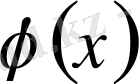 функцияның өзі және оның туындысы
функцияның өзі және оның туындысы
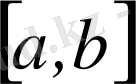 сегментте не үзіліссіз, не саны санаулы нүктеде бірінші түрдегі үзілісті болса, онда
сегментте не үзіліссіз, не саны санаулы нүктеде бірінші түрдегі үзілісті болса, онда
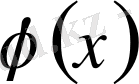 функция
функция
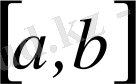 сегментте
бөлікті - тегіс функция
деп аталады.
сегментте
бөлікті - тегіс функция
деп аталады.
Функция сегментте Дирихле шартын қанағаттандырады деп аталады, егер сегментті саны санаулы дербес сегменттерге бөлгенде осы дербес сегменттердің әрқайсысының ішінде функция монотонды әрі шектеулі болса.
Математикалық анализ курсында ([14, 16] )
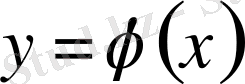 функцияның
функцияның
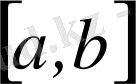 сегментте интегралдану анықтамасы мына түрде берілген:
сегментте интегралдану анықтамасы мына түрде берілген:
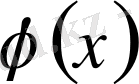 функция
функция
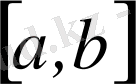 сегментте
интегралданады
деп аталады, егер
сегментте
интегралданады
деп аталады, егер
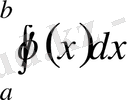 интегралы (меншікті не меншіксіз) бар болса. Онда
интегралы (меншікті не меншіксіз) бар болса. Онда
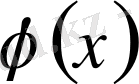 функция сегментте не үзіліссіз, не осы сегментте саны санаулы үзілісті нүктелердің маңайында функция шектелген немесе шектелмеген болуы мүмкін. Осы курста, саны санаулы нүктеде үзілісті функция үшін
функция сегментте не үзіліссіз, не осы сегментте саны санаулы үзілісті нүктелердің маңайында функция шектелген немесе шектелмеген болуы мүмкін. Осы курста, саны санаулы нүктеде үзілісті функция үшін
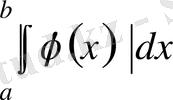 интегралы бар болса, онда
интегралы бар болса, онда
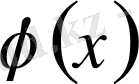 функцияның осы сегментте интегралданатыны дәлелденген. Сонымен, егер
функцияның осы сегментте интегралданатыны дәлелденген. Сонымен, егер
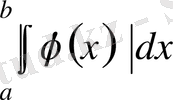 интегралы бар болса, онда
интегралы бар болса, онда
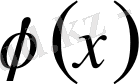 функция
функция
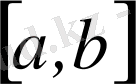 сегментте
абсолютті интегралданады
деп аталады.
сегментте
абсолютті интегралданады
деп аталады.
Бізге берілген
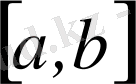 сегментті
сегментті
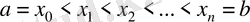 нүктелермен бөліктерге бөлейік. Егер әр бөліктегі функцияның мәні тұрақты болса, онда ол функция
сатылы функция
деп аталады.
нүктелермен бөліктерге бөлейік. Егер әр бөліктегі функцияның мәні тұрақты болса, онда ол функция
сатылы функция
деп аталады.
Функция
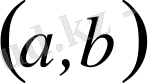 интервалда
сипаттамалы функция
деп аталады, егер
интервалда
сипаттамалы функция
деп аталады, егер
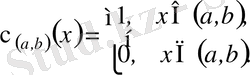
Егер
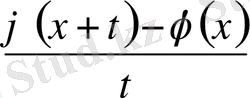 функция
функция
 сегментте қосындылы функция болса, яғни
сегментте қосындылы функция болса, яғни
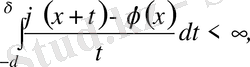
онда бұл шарт
Дини шарты
деп аталады. Мысалы,
 дәрежелі
Лившиц шарты
деп аталатын мына шарт орындалса(
дәрежелі
Лившиц шарты
деп аталатын мына шарт орындалса(
 ) :
) :
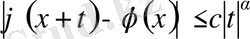 ,
,
мұндағы
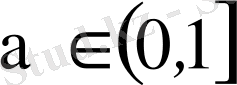 , онда
, онда
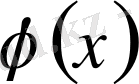 функция үшін Дини шарты орындалады. Осы сияқты, егер
функция үшін Дини шарты орындалады. Осы сияқты, егер
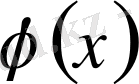 функцияның
функцияның
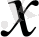 нүктеде шектеулі туындысы бар болса, онда
нүктеде шектеулі туындысы бар болса, онда
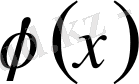 функцияға бірінші дәрежелі Лившиц шарты орындалады.
функцияға бірінші дәрежелі Лившиц шарты орындалады.
Анақтама.
Кез келген
 жиын
метрикалық кеңістік
деп аталады, егер:
жиын
метрикалық кеңістік
деп аталады, егер:
1)
 жиынның кез келген
жиынның кез келген
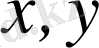 элементтеріне осы элементтердің
ара қашықтығы
деп аталатын
элементтеріне осы элементтердің
ара қашықтығы
деп аталатын
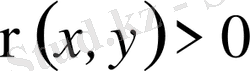 саны табылса;
саны табылса;
2)
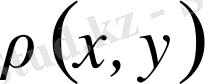 ара қашықтыққа мына аксиомалар орындалса;
ара қашықтыққа мына аксиомалар орындалса;
2 а)
, егер
( тепе-теңдік аксиомасы ),
2 б)
( симметриялы аксиомасы ),
2 в)
( үшбұрыш аксиомасы ) .
Анықтамада келтірілген аксиомалар
 кеңістіктегі
метриканың аксиомалары
деп аталады.
кеңістіктегі
метриканың аксиомалары
деп аталады.
Мысалы, барлық
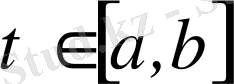 үшін үзіліссіз функциялар жиынындағы
үшін үзіліссіз функциялар жиынындағы
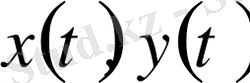 функциялардың ара қашықтығын немесе үзіліссіз функциялар жиынындағы метриканы мына формула арқылы анықтасақ:
функциялардың ара қашықтығын немесе үзіліссіз функциялар жиынындағы метриканы мына формула арқылы анықтасақ:
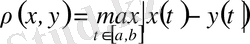 , онда бұл метрика метриканың аксиомаларын қанағаттандырады, яғни бұл жиын метрикалық кеңістік болады. Сонымен,
, онда бұл метрика метриканың аксиомаларын қанағаттандырады, яғни бұл жиын метрикалық кеңістік болады. Сонымен,
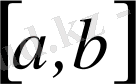 сегментте анықталған үзіліссіз функциялар жиынында
сегментте анықталған үзіліссіз функциялар жиынында
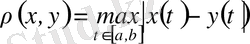 метрикамен анықталған жиын метрикалық кеңістік болады және ол
метрикамен анықталған жиын метрикалық кеңістік болады және ол
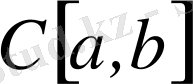 таңбамен белгіленеді.
таңбамен белгіленеді.
Осы сияқты,
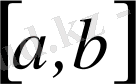 сегментте анықталған үзіліссіз функциялар жиынында метрика
сегментте анықталған үзіліссіз функциялар жиынында метрика
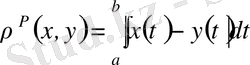
түрінде анықталса, онда
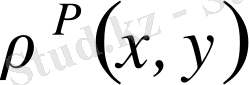 метрика метриканың барлық аксиомаларын қанағаттандырады және ол жиын немесе кеңістік
метрика метриканың барлық аксиомаларын қанағаттандырады және ол жиын немесе кеңістік
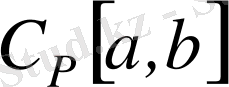 таңбамен белгіленеді.
таңбамен белгіленеді.
Анықтама.
Кез келген
 жиын
сызықты
нормаланған кеңістік
деп аталады, егер:
жиын
сызықты
нормаланған кеңістік
деп аталады, егер:
- сызықты кеңістік;
- метрикалық кеңістік;
- элементтердінүктеге ара қашақтығы өзгермесе, яғни, мұндағы;
- .
Осы анықтамадағы 3) шарттан мына теңдік орындалады:
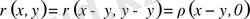
Мына ара қашықтық
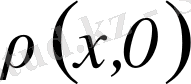 (
(
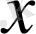 элементтен нөл элементке дейінгі ара қашықтық)
элементтен нөл элементке дейінгі ара қашықтық)
 кеңістіктегі
кеңістіктегі
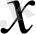 элементтің нормасы
деп аталады және ол норма
элементтің нормасы
деп аталады және ол норма
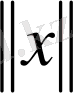 немесе
немесе
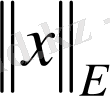 таңбамен белгіленеді әрі нормаға мына шарттар орындалады:
таңбамен белгіленеді әрі нормаға мына шарттар орындалады:
а)
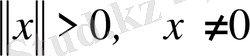 ; егер
; егер
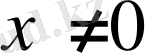 болса, онда
болса, онда
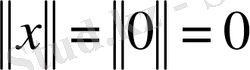 ;
;
б)
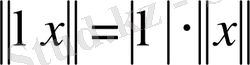 ;
;
в)
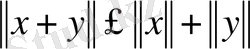 .
.
Жоғарыда қарастырылған
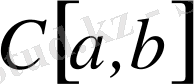 метрикалық кеңістіктің
метрикалық кеңістіктің
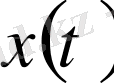 элементінің нормасы:
элементінің нормасы:
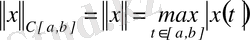 , ал
, ал
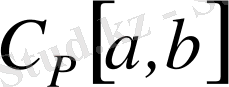 кеңістіктегі
кеңістіктегі
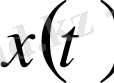 элементтің нормасы:
элементтің нормасы:
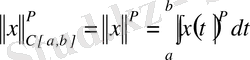 болады.
болады.
 сегментте анықталған әрі
сегментте анықталған әрі
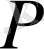 дәрежелі өлшемді функциялар
жиыны
дәрежелі өлшемді функциялар
жиыны
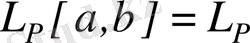 таңбамен белгіленеді және оның элементтерінің нормасы
таңбамен белгіленеді және оның элементтерінің нормасы
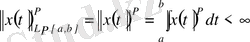
формуладан анықталады, мұндығы интеграл Лебег интегралы,
 - оң сан. Егер
- оң сан. Егер
 ,
,
 болса, онда
болса, онда
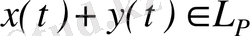 ,
,
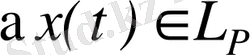 - кез келген сан. Егер
- кез келген сан. Егер
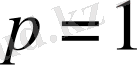 болғандағы кеңістік
болғандағы кеңістік
 таңбамен белгіленеді және
таңбамен белгіленеді және
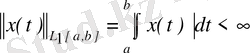
Егер
 болса, онда
болса, онда
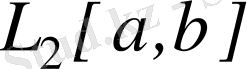 -
квадратымен қосындылы кеңістік
деп аталады және
-
квадратымен қосындылы кеңістік
деп аталады және
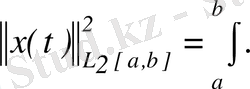
Фубини теоремасы.
Егер
 функция
функция
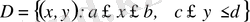 тікбұрышты облыста қосындылы функция болса, онда:
тікбұрышты облыста қосындылы функция болса, онда:
- кез келген - функция қосындылы функция;
- жоғарыдағы 1) шарт орындалғанда мына интеграл-ке тәуелді функция барлықүшін қосындылы функция;
- мына теңдік орындалады:
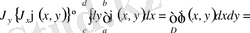
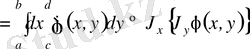 .
.
Ескерту.
Мына интегралдың бар болуынан
 , өлшемді
, өлшемді
 жиынында олардың теңдігі мен
жиынында олардың теңдігі мен
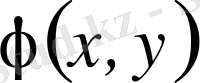 функцияның қосындылы функция болуы шықпайды. Бірақта, егер өлшемді
функцияның қосындылы функция болуы шықпайды. Бірақта, егер өлшемді
 жиында
жиында
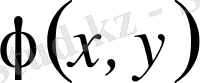 өлшемді әрі оң функция болса және екі еселі интегралдардың біреуі бар болса, онда екіншісі де бар болады және мына теңдік орындалады:
өлшемді әрі оң функция болса және екі еселі интегралдардың біреуі бар болса, онда екіншісі де бар болады және мына теңдік орындалады:
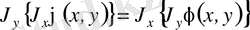 .
.
Анықтама.
 метрикалық кеңістік
компакты
деп аталады, егер
метрикалық кеңістік
компакты
деп аталады, егер
 кеңістікке тиісті кез келген шексіз
кеңістікке тиісті кез келген шексіз
 жиыншада фундаменталды тізбек бар болса.
жиыншада фундаменталды тізбек бар болса.
Мысалы, математикалық анализ курсындағы Больцано-Вейерштрасс теоремасы бойынша ([14, 16]
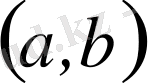 интервалдағы кез келген
интервалдағы кез келген
 шексіз жиыншада шектік нүкте бар, олай болса
шексіз жиыншада шектік нүкте бар, олай болса
 жиында фундаментальді тізбек бар, яғни
жиында фундаментальді тізбек бар, яғни
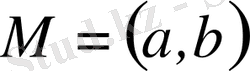 интервалы компакты метрикалық кеңістік болады.
интервалы компакты метрикалық кеңістік болады.
Алдағы тақырыпта бізге қажет болатын мына меншіксіз интегралды есептейік:
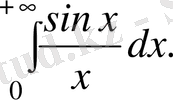
Ол үшін,
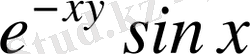 функцияны
функцияны
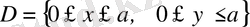 облыста
облыста
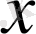 және
және
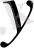 айнымалар бойынша интегралдайық:
айнымалар бойынша интегралдайық:
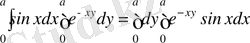 (3. 1)
(3. 1)
Теңдіктің оң жағындағы ішкі интегралды екі рет бөліктеп интегралдайық, ал сол жағындағы ішкі интегралды есептейік, сонда
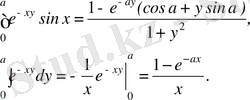
Осыдан (3. 1) теңдіктің оң жағындағы интеграл мына түрге:
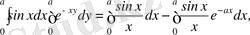
ал оң жағындағы интеграл мына түрге түрленеді:
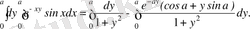
Соңғы екі теңдіктің оң жақтарын теңестірейік:
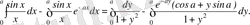 (3. 2)
(3. 2)
Енді (3. 2) теңдіктің сол жағындағы екінші интегралды бағалайық:
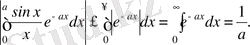
Осы сияқты, (3. 2) теңдіктің оң жағындағы екінші интегралды бағаласақ, онда ол
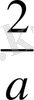 санынан кіші болады. Сондықтан
санынан кіші болады. Сондықтан
 -да шекке көшсек, онда
-да шекке көшсек, онда
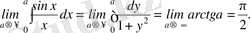
Осыдан
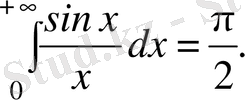 (3. 3)
(3. 3)
3. 2. Тригонометриялық қатардың бірқалыпты
жинақтылығы
Математикалық анализ курсының практикалық есептерінде
 сегментте
сегментте
 функцияны тригонометриялық Фурье қатарына жіктеуге тура келеді:
функцияны тригонометриялық Фурье қатарына жіктеуге тура келеді:
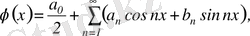 (3. 4)
(3. 4)
мұндағы (3. 4) теңдіктің оң жағындағы қатар
тригонометриялық қатар
деп аталады, ал
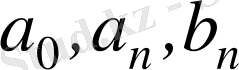 -
Фурье коэффициенттері
деп аталатын коэффициенттер мына формулалардан анықталады:
-
Фурье коэффициенттері
деп аталатын коэффициенттер мына формулалардан анықталады:
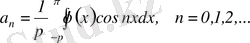 (3. 5)
(3. 5)
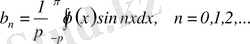 (3. 6)
(3. 6)
3. 1-теорема.
Егер периоды
 -ге тең
-ге тең
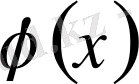 функция (3. 4) теңдіктің оң жағындағы қатарға жіктелсе және ол қатар барлық сандар өсінде
функция (3. 4) теңдіктің оң жағындағы қатарға жіктелсе және ол қатар барлық сандар өсінде
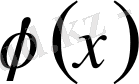 функцияға бірқалыпты жинақты болса, онда бұл тригонометриялық қатар
функцияға бірқалыпты жинақты болса, онда бұл тригонометриялық қатар
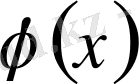 функцияның Фурье қатары болады.
функцияның Фурье қатары болады.
Дәлелдеуі.
Берілген
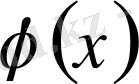 функция үшін (3. 4) теңдік орындалсын және (3. 4) теңдіктің оң жағындағы тригонометриялық қатар бірқалыпты жинақты болсын. Онда
функция үшін (3. 4) теңдік орындалсын және (3. 4) теңдіктің оң жағындағы тригонометриялық қатар бірқалыпты жинақты болсын. Онда
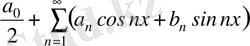 . (3. 7)
. (3. 7)
функциялық қатардың қосындысы үзіліссіз функция болады және бұл қатарды мүшелеп интегралдауға болады. Енді (3. 4) теңдіктің екі жағын
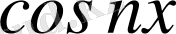 ке көбейтейік:
ке көбейтейік:
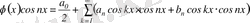 . (3. 8)
. (3. 8)
Соңғы теңдіктің оң жағындағы қатардың бірқалыпты жинақты болатынын дәлелдейік. Ол үшін осы қатардың дербес қосындысын қарастырайық:
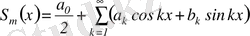 .
.
Кез келген
 санын алайық. Тригонометриялық (3. 7) қатар бірқалыпты жинақты болғандықтан,
санын алайық. Тригонометриялық (3. 7) қатар бірқалыпты жинақты болғандықтан,
 саны табылады және
саны табылады және
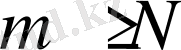 теңсіздікті қанағаттандыратын барлық
теңсіздікті қанағаттандыратын барлық
 сандар үшін
сандар үшін
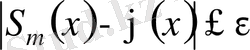
теңсіздігі орындалады. Мұнда
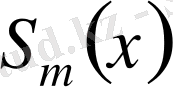 қосынды (3. 7) тригонометриялық қатардың дербес қосындысы болғандықтан,
қосынды (3. 7) тригонометриялық қатардың дербес қосындысы болғандықтан,
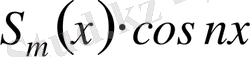 көбейтінді де (3. 8) тригонометриялық қатардың дербес қосындысы болады. Онда
көбейтінді де (3. 8) тригонометриялық қатардың дербес қосындысы болады. Онда
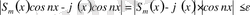
теңсіздігі
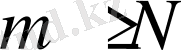 теңсіздікті қанағаттандырытың барлық
теңсіздікті қанағаттандырытың барлық
 сандар үшін орындалады. Демек, (3. 8) қатар бірқалыпты жинақты болады, онда (3. 8) қатарды мүшелеп интегралдауға болады. Енді (3. 8) қатарды мүшелеп интегралдап, (3. 5) теңдікті аламыз. Осы сияқты, (3. 8) теңдікті
сандар үшін орындалады. Демек, (3. 8) қатар бірқалыпты жинақты болады, онда (3. 8) қатарды мүшелеп интегралдауға болады. Енді (3. 8) қатарды мүшелеп интегралдап, (3. 5) теңдікті аламыз. Осы сияқты, (3. 8) теңдікті
 -ке көбейтіп, (3. 6) теңдікті аламыз. Олай болса, (3. 4) қатар Фурье қатары болады. Дәлелденді.
-ке көбейтіп, (3. 6) теңдікті аламыз. Олай болса, (3. 4) қатар Фурье қатары болады. Дәлелденді.
3. 2-теорема.
Егер периоды
 -ге тең абсолютті интегралданатын
-ге тең абсолютті интегралданатын
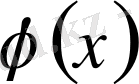 функция (3. 4) теңдіктің оң жағындағы қатарға жіктелсе және ол қатар периоды бірдей саны санаулы үзілісті нүктелерден өзге нүктелердің бәрінде
функция (3. 4) теңдіктің оң жағындағы қатарға жіктелсе және ол қатар периоды бірдей саны санаулы үзілісті нүктелерден өзге нүктелердің бәрінде
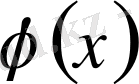 функцияға жинақты болса, онда бұл қатар Фурье қатары болады.
функцияға жинақты болса, онда бұл қатар Фурье қатары болады.
3. 3. Фурье қатарының комплекс түрі
Бізге периоды
 -ге тең,
-ге тең,
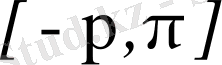 сегментте саны санаулы үзілісті нүктесі бар әрі осы сегментте абсолютті интегралданатын
сегментте саны санаулы үзілісті нүктесі бар әрі осы сегментте абсолютті интегралданатын
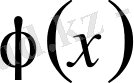 функция берілсін және тригонометриялық қатар Фурье қатары болсын, яғни (3. 4) теңдік орындалсын. Қатардың жалпы мүшесін (2. 9-тақырып) Эйлер формуласы бойынша түрлендірейік:
функция берілсін және тригонометриялық қатар Фурье қатары болсын, яғни (3. 4) теңдік орындалсын. Қатардың жалпы мүшесін (2. 9-тақырып) Эйлер формуласы бойынша түрлендірейік:
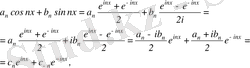
мұндағы
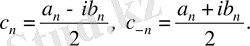
Енді
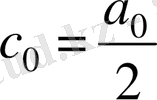 болсын, онда (3. 7) қатардың дербес қосындысы мына түрге түрленеді:
болсын, онда (3. 7) қатардың дербес қосындысы мына түрге түрленеді:
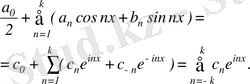 (3. 9)
(3. 9)
Осы (3. 7) қатардың (3. 5) бен (3. 6) коэффициенттерін жаңа
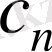 коэффициент арқылы түрлендірейік:
коэффициент арқылы түрлендірейік:
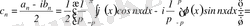
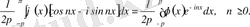
Енді (3. 4) теңдікті ескеріп, (3. 9) теңдіктен
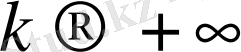 -да шекке көшейік:
-да шекке көшейік:
Сонымен, егер
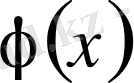 функция (3. 7) тригонометриялық қатардың қосындысы болса, онда
функция (3. 7) тригонометриялық қатардың қосындысы болса, онда
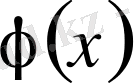 функцияның Фурье қатарының комплекс түрі мына түрде жазылады:
функцияның Фурье қатарының комплекс түрі мына түрде жазылады:
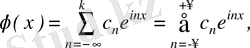 (3. 10)
(3. 10)
мұндағы
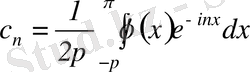 ,
,
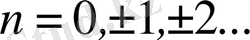 (3. 11)
(3. 11)
Егер
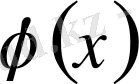 функцияның периоды
функцияның периоды
 болса, онда Фурье қатарының комплекс түрі мына түрде жазылады:
болса, онда Фурье қатарының комплекс түрі мына түрде жазылады:
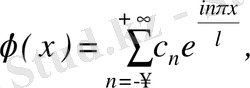 (3. 12)
(3. 12)
мұндағы
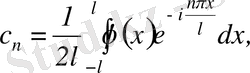 ,
,
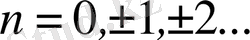 (3. 13)
(3. 13)
Жоғарыдағы (3. 10) мен (3. 11) формулалар Фурье қатарының комплекс түрі деп аталады.
3. 4. Фурье қатарының жинақтылығы
Біз
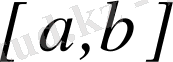 сегментте қосындылы
сегментте қосындылы
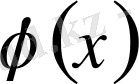 функцияны қарастырайық.
функцияны қарастырайық.
3. 3-теорема.
Егер
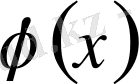 функция
функция
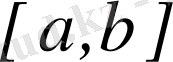 сегментте қосындылы функция болса, онда мына интегралдар:
сегментте қосындылы функция болса, онда мына интегралдар:
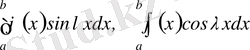
 да нөлге ұмтылады.
да нөлге ұмтылады.
Дәлелдеуі.
Берілген
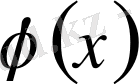 функция
функция
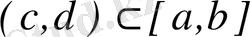 интервалда сипаттамалық функция болсын. Онда
интервалда сипаттамалық функция болсын. Онда
 да
да
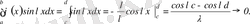
Кез келген сатылы
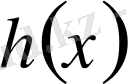 функция
функция
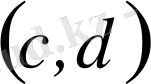 интервалдағы сипаттамалы функциялардың сызықты комбинациясы болады. Сондықтан, сатылы функция үшін теорема дәлелденді.
интервалдағы сипаттамалы функциялардың сызықты комбинациясы болады. Сондықтан, сатылы функция үшін теорема дәлелденді.
Егер
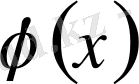 кез келген қосындылы функция болса, онда берілген
кез келген қосындылы функция болса, онда берілген
 саны үшін
саны үшін
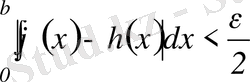
теңсіздігі орындалатын
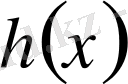 сатылы функцияны таба аламыз және
сатылы функцияны таба аламыз және
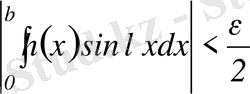
теңсіздік орындалатындай
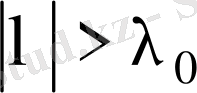 теңсіздікті қанағаттандыратын
теңсіздікті қанағаттандыратын
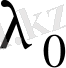 оң санды табамыз. Онда жоғарыда анықталған
оң санды табамыз. Онда жоғарыда анықталған
 мәндер үшін мына теңсіздік орындалады:
мәндер үшін мына теңсіздік орындалады:
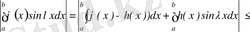

Теореманың екінші тұжырымы осы сияқты дәлелденеді. Дәлелденді.
Осы теоремадан мына салдарды аламыз.
Салдар.
Кез келген интегралданатын
 функцияның Фурье қатарының коэффициенттері
функцияның Фурье қатарының коэффициенттері
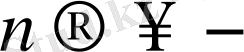 да нөлге ұмтылады, яғни
да нөлге ұмтылады, яғни
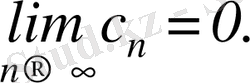
3. 4-теорема.
Егер қосындылы
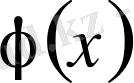 үшін мына интеграл
үшін мына интеграл
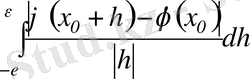
жинақты болса, онда
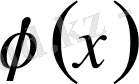 функцияның Фурье қатарының дербес қосындысы
функцияның Фурье қатарының дербес қосындысы
 нүктеде
нүктеде
 мәнге жинақты болады.
мәнге жинақты болады.
Дәлелдеуі.
Теореманы дәлелдеу үшін (3. 10) Фурье қатарының
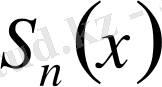 дербес қосындысын түрлендірейік:
дербес қосындысын түрлендірейік:
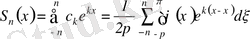 .
.
Соңғы теңдікке
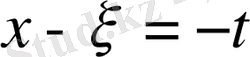 алмастыруын қолданайық және
алмастыруын қолданайық және
 функцияны
функцияны
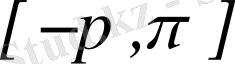 сегменттен бастап периоды
сегменттен бастап периоды
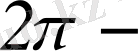 ге тең болатындай етіп, бүкіл сандар өсінде жалғастырайық. Онда
ге тең болатындай етіп, бүкіл сандар өсінде жалғастырайық. Онда
 айнымалы бойынша алынған интегралдың жаңа
айнымалы бойынша алынған интегралдың жаңа
 , интегралдау шектерін сәйкес
, интегралдау шектерін сәйкес
 мен
мен
 ге алмастыруға болады, сонда
ге алмастыруға болады, сонда
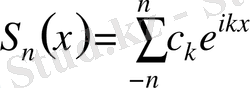
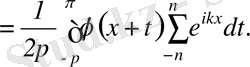 (3. 14)
(3. 14)
Интеграл астындағы қосындыны табайық (геометриялық прогрессия)
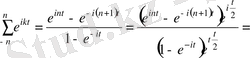
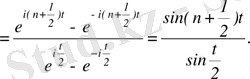
Сонда (3. 14) дербес қосынды мына түрге түрленеді:
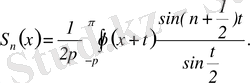 (3. 15)
(3. 15)
Интеграл астындағы
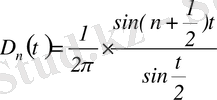
функция
Дирихле ядросы
деп аталады. Егер
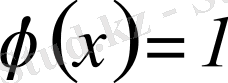 болса, онда кез келген
болса, онда кез келген
 үшін
үшін
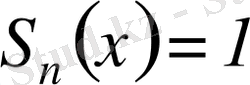 болады. Енді
болады. Енді
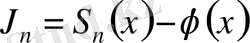 айырымды бағалайық:
айырымды бағалайық:
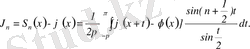 (3. 16)
(3. 16)
Егер
 -да
-да
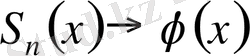 болса, онда (3. 16) айырым нөлге ұмтылады. Демек, теореманы дәлелдеу үшін соңғы тұжырымды дәлелдесек жеткілікті. Ол үшін
Дини шарты
орындалсын және тағайындалған
болса, онда (3. 16) айырым нөлге ұмтылады. Демек, теореманы дәлелдеу үшін соңғы тұжырымды дәлелдесек жеткілікті. Ол үшін
Дини шарты
орындалсын және тағайындалған
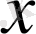 үшін қосындылы
үшін қосындылы
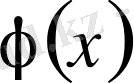 функция анықталсын әрі шектеулі болсын және Дини шарты орындалсын, яғни
функция анықталсын әрі шектеулі болсын және Дини шарты орындалсын, яғни
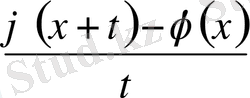
функция
 теңсіздікті қанағаттандыратын барлық
теңсіздікті қанағаттандыратын барлық
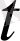 бойынша интегралдансын, яғни барлық
бойынша интегралдансын, яғни барлық
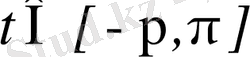 үшін интегралдансын. Онда
үшін интегралдансын. Онда
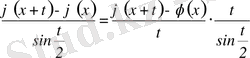
функция да
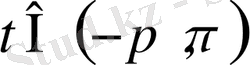 интервалда интегралданады және (3. 16) интегралға 3. 3- теореманы пайдалануға болады. Онда, 3. 3- теорема бойынша,
интервалда интегралданады және (3. 16) интегралға 3. 3- теореманы пайдалануға болады. Онда, 3. 3- теорема бойынша,
 да
да
 интеграл нөлге ұмтылады. Дәлелденді.
интеграл нөлге ұмтылады. Дәлелденді.
3. 5. Фурье қатарының бірқалыпты жинақтылығы
3. 5-теорема.
Егер қосындылы
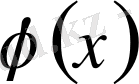 функция
функция
 жиында шектелсе және Дини шарты бірқалыпты орындалса, яғни кез келген
жиында шектелсе және Дини шарты бірқалыпты орындалса, яғни кез келген
 сан үшін
сан үшін
 саны табылып,
саны табылып,
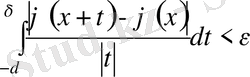
теңсіздік барлық
 үшін орындалса, онда
үшін орындалса, онда
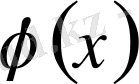 функцияның Фурье қатары
функцияның Фурье қатары
 жиынында
жиынында
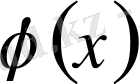 функцияға бірқалыпты жинақты болады.
функцияға бірқалыпты жинақты болады.
Дәлелдеуі.
Теореманы дәлелдеу үшін дәлелдеусіз мына тұжырымды қабыл алайық:
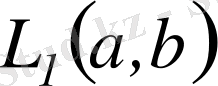 кеңістігіндегі метрика бойынша компактылы болатын кез келген
кеңістігіндегі метрика бойынша компактылы болатын кез келген
 қосындылы функциялар
қосындылы функциялар
 жиынында мына шек
жиынында мына шек
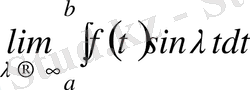
нөлге бірқалыпты жинақты болады.
Енді теореманы дәлелдейік. Алдын ала тағайындалған
 санына барлық
санына барлық
 үшін
үшін
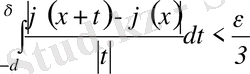 (3. 16)
(3. 16)
теңсіздігі орындалатындай
 санын тауып алуға болады. Онда Фурье қатарының
санын тауып алуға болады. Онда Фурье қатарының
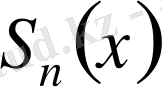 дербес қосындысы мен
дербес қосындысы мен
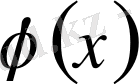 функцияның айырымын түрлендірейік, мұндағы
функцияның айырымын түрлендірейік, мұндағы
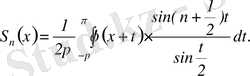 (3. 17)
(3. 17)
Сонда
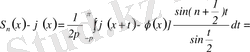

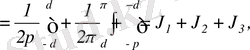
,
мұндағы
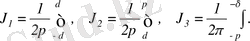
Енді осы айырымды бағалайық. Интеграл астындағы
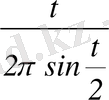 функцияға
функцияға
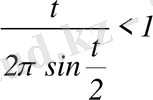 теңсіздік орындалады. Онда, (3. 16) теңсіздіктен
теңсіздік орындалады. Онда, (3. 16) теңсіздіктен
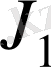 қосылғыш үшін мына теңсіздік орындалады, барлық
қосылғыш үшін мына теңсіздік орындалады, барлық
 үшін:
үшін:
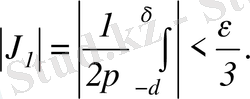
Енді
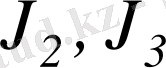 қосындыларды бағалау үшін,
қосындыларды бағалау үшін,
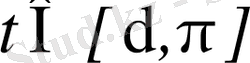 айнымалыға тәуелді және
айнымалыға тәуелді және
 параметрлі мына функциялар
параметрлі мына функциялар
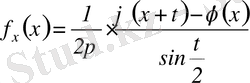
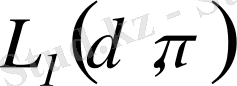 кеңістігінде компактылы
кеңістігінде компактылы
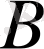 жиынды құрайтынын дәлелдейік. Ол үшін
жиынды құрайтынын дәлелдейік. Ол үшін
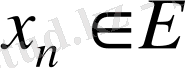 кез келген тізбек болсын, мұнда
кез келген тізбек болсын, мұнда
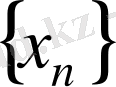 тізбекті
тізбекті
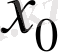 нүктеге жинақты болсын деп алуға да болады, онда
нүктеге жинақты болсын деп алуға да болады, онда
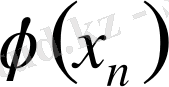 функция мәндері
функция мәндері
 санға жинақталады. Онда
санға жинақталады. Онда
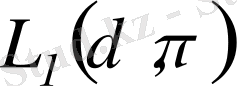 кеңістіктің метрикасынан
кеңістіктің метрикасынан
 -да
-да

Олай болса,
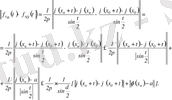
Онда,
 -да
-да
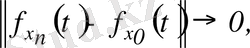
яғни
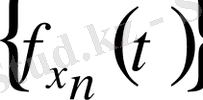 тізбек
тізбек
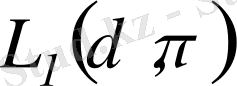 кеңістігінде фундаменталды (іргелі) тізбек болады. Олай болса,
кеңістігінде фундаменталды (іргелі) тізбек болады. Олай болса,
 жиын компактылы жиын болады. Енді дәлелдеусіз қабыл алған
тұжырым
бойынша, барлық
жиын компактылы жиын болады. Енді дәлелдеусіз қабыл алған
тұжырым
бойынша, барлық
 және
және
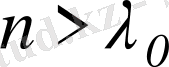 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 үшін мына теңсіздік
үшін мына теңсіздік
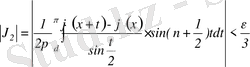
орындалатындай
 санын тауып алуға болады. Осы сияқты, (3. 17) формуладағы
санын тауып алуға болады. Осы сияқты, (3. 17) формуладағы
 қосынды үшін соңғы теңсіздікті дәлелдеуге болады. Сонымен, жеткілігінше үлкен
қосынды үшін соңғы теңсіздікті дәлелдеуге болады. Сонымен, жеткілігінше үлкен
 үшін
үшін
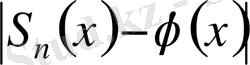 шама
шама
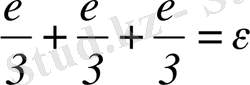 -нан кіші болады, барлық
-нан кіші болады, барлық
 үшін. Дәлелденді.
үшін. Дәлелденді.
3. 6. Фурье түрлендіруі
Периоды
 -ге тең
-ге тең
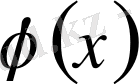 функцияны гармоникалық тербеліс арқылы өрнектеу керек болса, біз Фурье қатарын пайдаланамыз:
функцияны гармоникалық тербеліс арқылы өрнектеу керек болса, біз Фурье қатарын пайдаланамыз:
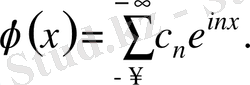 (3. 18)
(3. 18)
Периоды
 -ге тең функция үшін Фурье қатары мына түрде жазылады:
-ге тең функция үшін Фурье қатары мына түрде жазылады:
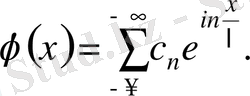 (3. 19)
(3. 19)
Соңғы (3. 19) теңдікті
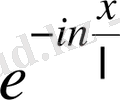 функцияға көбейтіп,
функцияға көбейтіп,
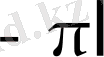 -ден
-ден
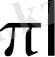 -ге дейін
-ге дейін
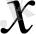 бойынша интегралдайық. Сонда
бойынша интегралдайық. Сонда
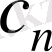 Фурье коэффициенттері мына формуладан анықталады:
Фурье коэффициенттері мына формуладан анықталады:
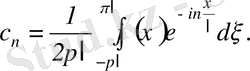 (3. 20)
(3. 20)
Енді (3. 19) бен (3. 20) теңдіктерден мына теңдікті аламыз:
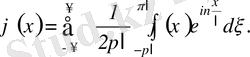 (3. 21)
(3. 21)
Егер (3. 21) интегралдан
 -да
шекке көшуге болатын
болса
, онда
-да
шекке көшуге болатын
болса
, онда
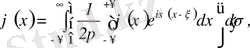 (3. 22)
(3. 22)
мұндағы
 аргумент
аргумент
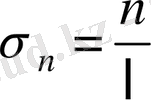 дискретті аргументтен алынған үзіліссіз аргумент. Сонымен, егер (3. 21) формуладан
дискретті аргументтен алынған үзіліссіз аргумент. Сонымен, егер (3. 21) формуладан
 -да шек бар болған жағдайда
-да шек бар болған жағдайда
 функция гармоникалық тербеліс арқылы мына формуладан анықталады:
функция гармоникалық тербеліс арқылы мына формуладан анықталады:
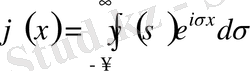 , (3. 23)
, (3. 23)
мұндағы
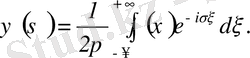 (3. 24)
(3. 24)
(3. 24) формуладан анықталған
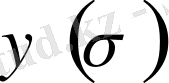 функция
функция
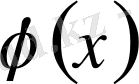 функцияның
Фурье түрлендіруі
немесе
Фурье интегралы
, ал (3. 23) формула
кері Фурье түрлендіруі
деп аталады. Кері Фурье түрлендіруінің Фурье түрлендіруінен айырмашылығы көрсеткіштік функцияның дәрежесіндегі таңбада және
функцияның
Фурье түрлендіруі
немесе
Фурье интегралы
, ал (3. 23) формула
кері Фурье түрлендіруі
деп аталады. Кері Фурье түрлендіруінің Фурье түрлендіруінен айырмашылығы көрсеткіштік функцияның дәрежесіндегі таңбада және
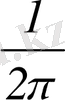 коэффициентте. Кейбір жағдайларда
Фурье түрлендіруін
мына түрде жазады:
коэффициентте. Кейбір жағдайларда
Фурье түрлендіруін
мына түрде жазады:
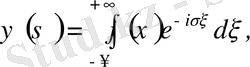 (3. 25)
(3. 25)
онда кері Фурье түрлендіруі мына түрде анықталады:
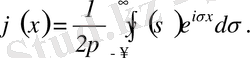 (3. 26)
(3. 26)
Фурье түрлендіруі мен оның кері түрлендіруі симметриялы болуы үшін көп жағдайда Фурье түрлендіруі мен оның кері Фурье түрлендіруін мына түрде анықтайды:
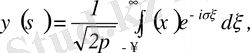 (3. 27)
(3. 27)
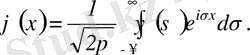 (3. 28)
Фурье түрлендіруі қай түрде жазылса да олар сызықты түрлендіру,
яғни Фурье түрлендіруі
(3. 28)
Фурье түрлендіруі қай түрде жазылса да олар сызықты түрлендіру,
яғни Фурье түрлендіруі
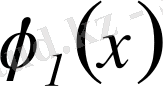 пен
пен
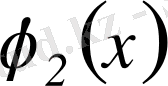 функциялардың қосындысын
функциялардың қосындысын
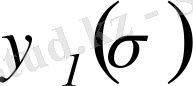 мен
мен
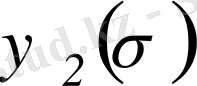 функциялар қосындысына ауыстырады және
функциялар қосындысына ауыстырады және
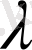 сан мен
сан мен
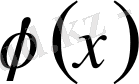 функцияның көбейтіндісін
функцияның көбейтіндісін
 мен
мен
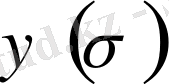 көбейтінділеріне ауыстырады.
көбейтінділеріне ауыстырады.
Біз төменде (3. 25) пен (3. 26) түрлендіруді қарастыратын боламыз.
3. 7. Фурье түрлендіруінің үзіліссіздігі
Жоғарыдағы 3. 6-тақырыпта,
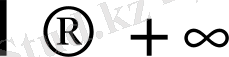 -да (3. 21) формуланың
шегі бар
болсын
деп үйғардық. Осы шектің
бар болуын
дәлелдеу
үшін,
-да (3. 21) формуланың
шегі бар
болсын
деп үйғардық. Осы шектің
бар болуын
дәлелдеу
үшін,
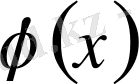 функция белгілі бір шарттарды қанағаттандырғанда (3. 25) теңдіктен (3. 26) теңдіктің орындалатынын дәлелдеуіміз керек.
функция белгілі бір шарттарды қанағаттандырғанда (3. 25) теңдіктен (3. 26) теңдіктің орындалатынын дәлелдеуіміз керек.
Егер
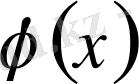 функция барлық
функция барлық
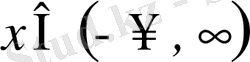 үшін интегралданса, онда
үшін интегралданса, онда
 ның барлық мәндері үшін
ның барлық мәндері үшін
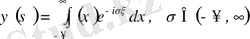
интегралы бар.
Онда
 функция
шектелген
әрі барлық
функция
шектелген
әрі барлық
 үшін
үзіліссіз
және
үшін
үзіліссіз
және
 -да
-да
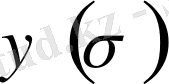 нөлге ұмтылады, яғни
нөлге ұмтылады, яғни
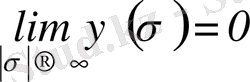 .
.
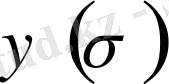 функцияның шектелгендігін мына теңсіздіктен аламыз:
функцияның шектелгендігін мына теңсіздіктен аламыз:
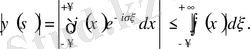
Осы теңсіздіктен мынадай қорытындыға келеміз:
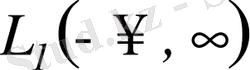 кеңістіктің метрикасы бойынша жинақты
кеңістіктің метрикасы бойынша жинақты
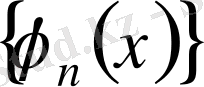 функциялық тізбекті Фурье түрлендіруі бірқалыпты жинақты
функциялық тізбекті Фурье түрлендіруі бірқалыпты жинақты
 функциялық тізбекке ауыстырады.
функциялық тізбекке ауыстырады.
Енді
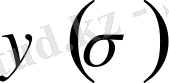 функцияның
үзіліссіздігі
мен оның
нөлге ұмтылуын
функцияның
үзіліссіздігі
мен оның
нөлге ұмтылуын
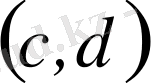 интервалдағы сипаттамалық функция үшін тексерейік. Онда
интервалдағы сипаттамалық функция үшін тексерейік. Онда
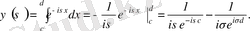
Соңғы теңдіктен
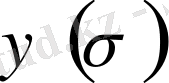 функцияның үзіліссіз функция болатынын және
функцияның үзіліссіз функция болатынын және
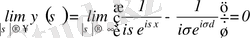
теңдік орындалатынын көреміз. Кез келген сатылы
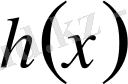 функция интервалдардағы сипаттамалық функциялардың сызықты комбинациясы болады, олай болса,
функция интервалдардағы сипаттамалық функциялардың сызықты комбинациясы болады, олай болса,
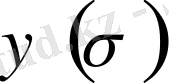 функцияның үзіліссіздігі мен нөлге ұмтылуы барлық сатылы функцияларға да орындалады. Сонымен, кез келген қосындылы
функцияның үзіліссіздігі мен нөлге ұмтылуы барлық сатылы функцияларға да орындалады. Сонымен, кез келген қосындылы
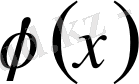 функция,
функция,
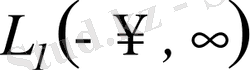 кеңістіктің метрикасы бойынша сатылы функциялардың шегі болады. Дәлелденген
кеңістіктің метрикасы бойынша сатылы функциялардың шегі болады. Дәлелденген
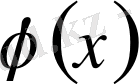 функцияның Фурье түрлендіруі
функцияның Фурье түрлендіруі
 өсіндегі бірқалыпты жинақты үзіліссіз функциялардың шегі болады. Онда
өсіндегі бірқалыпты жинақты үзіліссіз функциялардың шегі болады. Онда
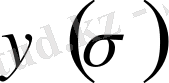 функцияның өзі де
функцияның өзі де
 өсінде үзіліссіз және
өсінде үзіліссіз және
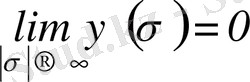 болады.
болады.
3. 8. Фурье түрлендіруінің формуласы
Осы тақырыпта, Фурье түрлендіруінің (3. 25) формуласынан (3. 26) формуланы қорытып шығарайық. Ол үшін (3. 26) формуланы шектеулі аралықта қарастырайық:
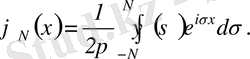
Осыдан және (3. 25) формуладан
 (3. 29)
(3. 29)
Соңғы теңдіктегі ішкі интеграл, яғни
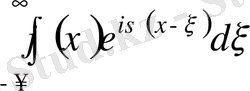
 параметр бойынша бірқалыпты жинақты, сондықтан (3. 29) формуладағы
параметр бойынша бірқалыпты жинақты, сондықтан (3. 29) формуладағы
 мен
мен
 бойынша интегралдау реттерін өзгертуге болады ([15] ) :
бойынша интегралдау реттерін өзгертуге болады ([15] ) :
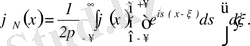
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz