Нақты сандар жиыны

Жоспар
Кіріспе

Нақты сандар жиыны
Шектелген жиындар
Жиын ұғымы
Рационал сандар
Вектор ұғымы және оған амалдар
Комплекс сандар
Оқиға және ықтималдық
Функцияның нүктедегі үздіксіздігі
Бірнеше айнымалы функция ұғымы және оның шегі, үздіксіздігі
Жұп, тақ және периодты функциялар
Күрделі функцияның туындысы мен дифференциалы

Барлық рационал және иррационал сандар бірігіп, нақты сангдар жиынын құрады. Барлық нақты сандар жиынын континуум деп атайды.
Нақты сандар жиынының қасиеттеріне тоқтап өтейік.
1 Нақты сандар жиыны – реттелген жиын, яғни егер α<β және β<γ болса, онда α<γ болады.
2 Нақты сандар жиынын, рационал сандар жиынындай, жаңа сандар қосып толықтыруға болмайды. Бұл қасиетті нақты сандар жиынының үздіксіздігі дейді.
Соңғы қасиетті дәлелдеу үшін барлық нақты сандар жиынына қима жүргіземіз.
Барлық нақты сандар жиынын екі класқа бөлейік: Оның біреуін Х арқылы, екіншісін У арқылы белгілейік. Сонда әрбір нақты сан не Х класына, не У класына жататын болсын және Х класына жататын әрбір нақты сан У класына жататын әрбір нақты саннан кіші болсын.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:

Нақты сандар жиыны

Барлық рационал және иррационал сандар бірігіп, нақты сангдар жиынын
құрады. Барлық нақты сандар жиынын континуум деп атайды.
Нақты сандар жиынының қасиеттеріне тоқтап өтейік.
1 Нақты сандар жиыны – реттелген жиын, яғни егер αβ және βγ болса,
онда αγ болады.
2 Нақты сандар жиынын, рационал сандар жиынындай, жаңа сандар қосып
толықтыруға болмайды. Бұл қасиетті нақты сандар жиынының үздіксіздігі
дейді.
Соңғы қасиетті дәлелдеу үшін барлық нақты сандар жиынына қима
жүргіземіз.
Барлық нақты сандар жиынын екі класқа бөлейік: Оның біреуін Х арқылы,
екіншісін У арқылы белгілейік. Сонда әрбір нақты сан не Х класына, не У
класына жататын болсын және Х класына жататын әрбір нақты сан У класына
жататын әрбір нақты саннан кіші болсын.
2-қасиеттің орнына келесі теореманы дәлелдесек болады.
Теорема. Нақты сандар жиынындағы қима (Х,У) ұандай болса да, төменгі
Х класын құрушы нақты сандардың ішінде ең үлкен сан бар (онда У класындағы
сандардың ішінде ең кішісі жоқ) немесе жоғарғы У класын құрушы нақты
сандардың ішінде ең кішісі бар (онда Х класындағы нақты сандардың ішінде ең
үлкені жоқ).
Бұл теореманы нақты сандар жиынының үздіксіздігі турасындағы теорема
деп атайды.
Тұжырымдалған теореманы былай дәлелдеуге болады. Х класын құрушы
нақты сандардың ішіндегі барлық рационал сандар жиынын А арқылы, ал У
класындағы барлық рационал сандар жиынын В арқылы белгілейік.
Сонда әрбір рационал сан не А класына, не В класына жатады және А
класына жататын әрбір рационал сан В класына жататын әрбір рационал саннан
кіші болады. Олай болса, (А,В) барлық рационал сандар жиынындағы қима болып
табылады. Сондықтан бұл қима бір тиянақты z санын анықтайды. z- не
рационал, не иррационал сан, қалай болған күннің өзінде ол бір нақты сан.
Айтылып отырған z саны не Х класына, не У класына жатуы керек. Егер бұл сан
Х класына жатса, онда ол осы класты құрушы сандардың ішіндегі ең үлкені
болып табылады. Міне осыны дәлелдеу керек. Айталық, z саны Х класындағы
барлық сандардың ішіндегі ең үлкенң болмасын. Онда Х класындағы сандардың
ішінен z санынан үлкен сан табылатын болады. Бұл сан t болсын. Сонымен,
tz. Осы z және t екі санның арасында жатқан ең болмағанда бір рационал r
саны табылады:
zrt.
r саны z санынан артық болғандықтан, ол r саны В жиынына
жатады.Ендеше r саны У класына жатады.Екінші жағынан r саны Х класына
жататын t санынан кіші, олай болса r саны Х класына жатады.Сөйтіп, r саны
бірдей екі класқа жататын болады. Ол мүмкін емес! Сонымен, Х класын құрушы
сандардың ішіндегі ең үлкені z емес деп ұйғару дұрыс болмайтын болды.
Міне, осы қайшылық Х класындағы сандардың ішінде ең үлкені z бар екенін
дәлелдейді. Онда, әрине, У класын құрушы сандардың ішінде ең кішісі жоқ.
Егер z саны У класына жатса, онда ол осы кластағы сандардың ең
кішісі болып табылады.Мұны да жанағыдай дәлелдейміз.
2.Жоғарыдағы келтірілген теорема геометрия тілінде аксиома болып
тұжырымдалады.
Аксиома.Егер түзудің бойындағы барлық нғктелер екі класқа
бөлінсе (олардың біреуі Х, екіншісі У болсын), түзудің әрбір нүктесі не Х
класына, не У класына жатса және Х класына жататын әрбір нүкте У класын
құратын әрбір нүктенің сол жағында болса, онда не Х класын құрушы
нүктелердің ішінде ең оң жақтағы шеткі нүкте бар (бұл жағдайда У класында
шеткі нүкте жоқ), не У класын құратын нүктелердің ішінде ең сол жақтағы
шеткі нүкте бар (онда Х класында шеткі нүкте жоқ).
Бұл аксиоманы түзудің үздіксіздігі турасындағы Дедекинд
аксиомасы дейді.
Жоғарыда дәлелденген теоремадан және Дедекинд аксиомасынан біз
мынадай қорытындыға келеміз: рационал және иррационал сандардан басқа жаңа
сандарды енгізіп, нақты сандар өрісін одан әрі кеңейтуге болмайды. Қазіргі
практикалық және теориялық мәселелердің санға келіп тірелетін барлық
мұқтаждарын нақты сандар толық шешеді.
Әрбір рационал санға түзудің бір, тек бір ғана рационал нүктесі
сәйкес келетінін және, керісінше, түзудің әрбір рационал нүктесіне тек
бір-ақ қана рационал сан сәйкес келеді. Былайша айтұанда, бүкіл рационал
сандар жиынымен, түзудің барлық рационал нүктелері жиынының арасында
өзара бірмәнді сәйкестік тағайындалды және мұнда былай: егер рационал сан
а, рационал b санынан кіші болса (ab), онда a-ға сәйкес келетін нүкте b-
ге сәйкес келетін нүктенің сол жағында жатады және керісінше.
Жоғарыдағы келтірілген теоремаға және аксиомаға сүйеніп, бүкіл нақты
сандар жиыны мен түзудің барлық нүктелері жиынының арасындағы өзара
бірмәнді сәйкестікті тағайындауға болады, және мұнда былай: егер z1, z2
түрлі екі нақты сан болса және z1z2 онда z1 санға сәйкес келетін нүкте
z2 санға сәйкес келетін нүктенің сол жағында жатады. Сонымен, бүкіл нақты
сандар жиыны мен түзудің барлық нүктелерінің жиыны бір-бірімен парапар.
Сондықтан нақты сандар жиынының орнына түзу нүктелерінің жиынын және,
керісінше, түзу нүктелері жиынының орнына нақты сандар жиынын қарастыруға
болады.
Барлық нақты сандар жиынының үздіксіздігі жөніндегі теорема немесе
түзудің үздіксіздігі жөніндегі аксиома математикалық анализдің фундаменті
болып табылады.

Шектелген жиындар

Нақты сандардан тұратын бір Е жиынын қарайық.
Егер осы Е жиынын құратын нақты сандардың қайсысын алсақ та, оның
шамасы бір L санынан аспаса, онда бұл жиынды жоғарғы жағынан немесе оң
жағынан шектелген жиын деп атайды. Егер Е жиынын құратын нақты сандардың
барлығы да бір l санынан артық болса, онда бұл жиынды төменгі жағынан
немесе сол жағынан шектелген жиын деп атайды.
L санын және одан артық сандарды, Е жиынының жоғарғы шекаралары дейді,
ал l санын және барлық одан кіші сандарды Е жиынының төменгі шекаралары
дейді.
Жоғарғы және төменгі жақтарынан шектелген жиынды шектелген немесе
шекараланған жиын деп атайды.
Осы ұғымға бірнеше мысалдар келтірейік.
1 Е жиыны келесі сандардан:
1, , , , ... , , ...
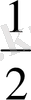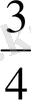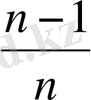тұратын болсын. Бұл жиын оң жағынан да, шектелген, өйткені жиынды құрып
тұрған сандардың қайсысын алсақ та, оның шамасы бірден аспайды және олардың
барлығы да 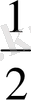– ден артық.
Келтірілген сандардан тұратын жиынның жоғарғы шекаралары 1 және
бірден артық сандардың барлығы; ал төменгі шекаралары 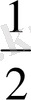және 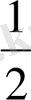-ден
кіші сандардың барлығы.
2 Е жиыны барлық натурал сандардан
1,2,3..., n, ...
тұрсын. Бұл жиын оң жағынан шектелмеген, тек сол жағынан ғана шектелген.
Сондықтан оны шектелген жиын деп айтуға болмайды. Бұл жиынның төменгі
шекаралары – бір және бірден кем сандардың барлығы.
3 Е жиыны мына сандардан:
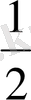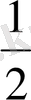2, 1, , 1, , 1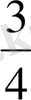, , 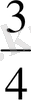..., 1 + , , ...
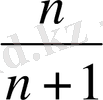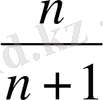тұратын болсын.
Бұл жиын жоғарғы жағынан да, төменгі жағынан да шектелген. Жоғарғы
шекаралары 2 және екіден артық сандардың барлығы; төменгі шекаралары
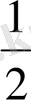және осы жартыдан кіші сандардың барлығы.
4 Е жиыны төменджегі теңсіздіктерді
a≤x≤b
қанағаттандыратын барлық нақты х сандардан тұрсын. Бұл жиын шектелген жиын,
жоғарғы шекаралары b және b-ден артық сандардың барлығы, ал төменгі
шекаралары а және а-дан кіші сандардың барлығы.
Айталық, Е – шектелген жиын болсын.
Е жиынының жоғарғы шекараларының ең кішісін оның дәл жоғарғы
шекаралығы немесе супремумы дейді және оны былай белгілейді: sup E.
Е жиынның төменгі шекараларының ең үлкенін оның дәл төменгі шекаралығы
немесе инфимумы дейді және оны былай белгілейді: inf E.
Бірінші мысалда дәл жоғарғы шекаралық немесе
sup E=1, ал дәл төменгі шекаралық немесе inf E=.
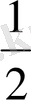Екінші мысалда inf E= + ∞, inf E= 1
Үшінші мысалда inf E= 2, inf E=
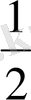
Төртінші мысалда inf E= b, inf E= a
Бұл келтірілген мысалдардан біз байқаймыз: дәл жоғарғы не дәл төменгі
шекаралықтар жиынның өзіне жатуы да және жатпауы да мүмкін.
Шектелген жиынның дәл шекаралықтары бола ма? Бұл сұраққа келесі
теорема жауап болып табылады.
Теорема. Егер Е х жиыны жоғары жағынан (төменгі жағынан) шектелсе,
онда ол жиынның әрқашан да дәл жоғарғы (дәл төменгі) шекаралығы болады.
Бұл теореманы дәлелдеу үшін екі жағдайды қарастыруға тура келеді:
Е жиынын құратын нақты х сандардың ішінде ең үлкен саны х арқылы
белгілейік. Онда Е жиынының барлығының құрамына х≤х теңсіздікті
қанағаттандырады, яғни х саны үшін жоғарғы шекаралық болып табылады.
Екінші жағынан х саны Е жиынының элементі, сондықтан бұл жиынның кез
келген L шекарасы үшін х саны мына х≤L теңсіздікті қанағаттандырады. Олай
болса, х саны – Е жиынының дәл жоғарғы шекаралығы.
б) Е жиынын құратын нақты х сандардың ішінде ең үлкені жоқ болсын.
Барлық нақты сандар жиынына (Х,У) қима жүргіземіз. Төменгі Х класына,
Е жиынын құратын сандардан кіші және оларға тең барлық нақты сандарды
жатқызайық, ал У класына Е жиынының барлық жоғарғы шекараларын жатқызамыз.
Сонымен, Х класына жататын нақты сандардың әрқайсысы, У класына
жататын нақты сандардың әрқайсысынан кіші болатын болады. Олай болса, (Х,У)
дедекиндтік қима, бұл қима бір нақты β санды анықтайды. Осы β саны Е
жиынының жоғарғы шекараларының ішіндегі ең кішісі болып табылатынына көз
жеткізу қиын емес.
Е жиынын құратын нақты х сандардың барлығы Х класына жататын
болғандықтан х≤β. Ендеше β саны – Е жиынының жоғарғы шекарасы. Ал, β санын
У класына жатқызуға болады, онда β сол кластағы ең кіші сан болып табылады;
У класы Е жиынының барлық жоғарғы шекараларынан тұрады, ендеше β- жоғарғы
шекаралардың ең кішісі. Сондықтан анықтама бойынша β=sup E
Енді дәл жоғарғы шекаралықтардың қасиеттерін санап өтейік:
1) Егер β саны Е {х} жиынының дәл жоғарғы шекаралығы болса,
онда х≤β.
2) Алдынала берілген оң ε саны қаншама аз болса да, Е жиынын
құратын сандардың ішінен мына хβ-ε теңсіздікті
қанағаттандыратын ең болмағанда бір нақты х санын табуға
болады.
3) Егер α саны Е {х} жиынының дәл төменгі шекаралығы болса,
онда х≥α.
4) Е жиынын құратын сандардың ішінен мына хα-ε теңсіздікті
қанағаттандыратын ең болмағанда бір х саны табылады, мұнда ε
– кез келген оң құнарсыз аз сан.

Жиын ұғымы

Қазіргі уақыттағы математикада үлкен роль атқаратын ұғымның бірі –
жиын ұғымы.
Жиын ұғымына анықтама беруге болмайды, былайша айтқанда; жиын ұғымы,
басқа жай ұғымдар арқылы анықтауға келмейтін, ең алғашқы ұғымдардың бірі
болып табылады. Сондықтан жиынның мағынансын түсіндіретін мысалдар
келтірейік. Жиын деген сөзден белгілібір қасиеттерге ие болып, белгілібір
заңмен бңрңккен әралуан заттарды (объектілерді) түсінуге болады. Мысалы,
кітаптың бетіндегі барлық әріптердің жиыны, берілген теңдеудің барлық
түбірлерінің жиыны, барлық оң сандар жиыны, барлық көпмұшелердің жиыны,
шеңбердің бойында жатқан барлық нүктелердің жиыны, сутегінің барлық
атомдарының жиыны т.т. туралы айтуға болады.
Жиынды құратын заттардың әрқайсысын оның элементі деп атайды. Мысалы,
нәрселерді санау процесі бізді натурал сандар 1,2,3,... жиынының ұғымына
келтіреді. Егер х М жиынының элементі болса, біз оны былай жазып
көрсетеміз: хεМ; егер элемент у М жиынына жатпайтын болса, оны біз былай
белгілейміз: уεМ. Тек А жиынының элементтеріне ғана тән Т қасиет белгілі
болса, А жиыны берілді дейміз.
Егер А жиынының барлық элементтері В жиынының да элементтері болатын
болса, онда А жиынын В жиынының бөлігі дейді, біз мұны мынадай символмен
А с В
жазып көрсетеміз. Мәселен, N барлық натурал сандар жиыны болса, ал М барлық
жұп сандар жиыны болса, онда М жиыны N жиынының бір бөлігі болады, яғни М с
N.
Сонымен, жиынның элементтері тіпті алуан заттар, әріптер, атомдар,
сандар, нүктелер, бұрыштар т.т. болатындығы келтірілген мысалдардан көрініп
тұр. Міне, бұл арада жиындар теориясының өте-мөте кеңдігі, оның ғылымның
(математика, механика, физика т.т.) көптеген салаларында қолданылатындығы
өзінен-өзі айқын.
Жиынның әрбір элементі болмауы да мүмкін, мұндай жиынды құр жиын деп
атайды. Мәселен, х2+1=0 теңдеудің барлық нақты түбірлерінің жиыны – құр
жиын.
Біздің келтірілген мысалдарымыздағы жиындар өздерінің элементтерінің
мөлшері жөнінде бәрі бірдей правода емес. Мәселен, кітаптың берілген
бетіндегі әріптердің саны шектеулі, өйткені оларды бірден санап, қанша
екенін білуге болады; сутегінің барлық атомдарының саны да шектеулі,
өйткені оларды бірден санап білмегенмен, атомдардың санынан асып кететін
санды әрқашан да жазып көрсетуге болады. Сонымен, әріптердің жиыны мен
атомдардың жиыны шектеулі жиын болды. Ал енді шеңбердің бойында жатұан
нүктелердің, барлық рационал сандардың, түзудің бойында жатқан нүктелердің
жиындары – шексіз жиындар.
Шексіз жиын деп қандай жиынды айту керек, бұған тоқталмай, берілген
шексіз жиындардың қайсысының элементтері көп, соны тексеру жолына көшейік.
Мысалы, жұп сандар мен бүтін сандардың қайсысы көп? Түзу кесіндісінің
бойында жатұан нүктелер мен квадрат ауданында жатқан нүктелердің қайсысының
саны артық? Осы мәселелерге жауап беру үшін мынадай бір мысалды қарайық:
Бір үлкен аудиторияның ішінде бірнеше орындықтар бар; лекция тыңдауға
келген студенттердің саны артық па, әлде аудиториядағы орындықтар саны
артық па? Әрине, біз мұны тексеру үшін аудиториядағы орындықтарды, содан
соң коридорда күтіп тұрған студенттерді санаған болар едік. Бұл мәселені
өйтпей-ақ та шешуге болады: егер аудиториядағы әрбір орындыққа тек бір ғана
студент отыратын болса, керісінше, бір студентке тек бір-ақ қана орындық
сәйкес келсе және мұндай операцияның нәтижесінде бос тұрған орындық
болмаса, ал сыртта орынсыз қалған студент болмаса, онда аудиториядағы
орындықтар мен студенттердің саны бірдей болғаны. Міне, осылай пар-парымен
үйлестіру принципін өзара бірмәнді сәйкестік деп атайды. Сонымен, егер
шекті екі жиынының элементтерінің саны бірдей болса, онда оларды
элементтерінің арасында өзара бірмәнді сәйкестікті тағайындауға болатын
болды.
Жұп сандар мен натурал сандардың мөлшерін салыстыру үшін оларды былай
жазайық:
1,2,3,4,5,6,7,8,9,...
2,4,6,8,10,12,14,16,18, ...
Бұл жазудан біз мынаны байқаймыз: жоғарғы қатардағы әрбір бүтін сан
өзінің астында тұрған төменгі қатардың бір ғана жұп санымен үйлеседі,
жоғарғы қатардағы және төменгі қатардағы сандардан ешбір парсыз қалып
қоятын сан жоқ. Сөйтіп, барлық натурал сандар қанша болса, жұп сандар да
сонша болады. Мұндағы таң қаларлық іс мынау: төменгі қатардағы жұп сандар
жоғарғы қатардағы натурал сандардың бір бөлігі, сөйтседағы екеуінің мөлшері
бірдей. Мұнда бір ескере кететін жағдай мынау: жоғарыда келтірілген шексіз
екі жиынның элементтерін пар-парымен үйлестіргенде қалай болса солай
үйлестірмейміз (мұны тек шекті жиындарға ғана жасауға болады, мәселен, қай
студент қай орындыққа отырады, оның бәрі бір), мәселен, төменгі қатардағы 2
жоғарғы қатардағы 2 мен, төменгі қатардағы 4 жоғарғы қатардағы 6 мен, сонан
әрі қарай үйлессін десек, онда жоғарғы қатардағы тақ сандар парсыз қалып
қояды. Міне, сондықтан қалай болса солай үйлестіруден бой тарту керек, яғни
бір белгілі ретпен үйлестіру керек.
Егер берілген А мен В екі жиынның элементтерінің арасында өзара
бірмәнді сәйкестік болса, онда мұндай жиындарды бір біріне баламалы
(эквивалент) жиындар деп атайды.
Егер екі жиын бір-бірімен баламалы болса, онда мұндай жиындардың
элементтерінің саны бірдей болғаны.
Барлық натурал сандар жиынына баламалы (эквивалент) жиынды саналатын
жиын деп аталады, былайша айтқанда, саналатын жиын деп элементтерін
номерлеп мынадай
а1, а2 ... ап,...
шексіз тізбек түрінде жазуға болатын жиынды айтады.
Егер жиынның элементтерінің саны барлық натурал сандардың санынан
артық болса, ондай жиын саналатын жиын болмайды, сондықтан мұндай жиынды
саналынбайтын жиын деп атайды. Мәселен, шеңбердің бойында, квадраттың
ауданында жатқан нүктелердің, ұзындығы қандай болса да түзудің
кескінділерінің барлық нүктелерінің жиындары саналынбайтын жиындарға
мысал болып табылады.

Рационал сандар

Адамзат мәдениетінің тууымен және оның дамуымен сан ұғымындай біте
қайнасқан басқа ұғымды көрсету немесе айту, сірә, қиын болар. Егер
адамзаттың қолдануынан осы ұғымды алып тастасақ, не болар еді? Сөз жоқ,
одан оның рухани өмірі тәжірибелік қайраты әлсіз болған болар еді. Ол
уақытта есеп –қисап жұмысын жүргізу, еңбек нәтижелерін қорыту, жалпы
алғанда, өлшеулер жүргізу мүмкіндіктері мүлде болмас еді.
Сонымен, адамзат тұрмысында сан ұғымы – ең керекті, ең маңызды, ең
қажетті ұғымдардың бірі.
Математика ғылымының негізгі ұүралы – натурал сандар –
1,2,3,4,5,6,7,8, ..., n, ...
Бұлардың негізгі құрал деп аталу себебі басқа сандар, мәселен,
рационал, иррационал сандар натурал сандардың туындысы болып табылады.
Басқаша айтқанда, натурал сандар математика ғылымының мықты фундаменті
болады.
Натурал сандар жеке нәрселерді санаудың нәтижесінен пайда болған. Олай
болса, нәрселерді санау, яғни олардың мөлшерлерін сипаттау, математикадағы
ең бірінші амал болатын болды.
Натурал сандар, саналатын объектілердің жеке өзіне тән түрлі
қасиеттерімен байланысты емес.
Тәжірибе мен теорияның мұқтаждығын, талабын толық қанағаттандыратындай
күшті құрал жасау үшін, натурал сандармен байланыстыра отырып, жалпы сан
ұғымын кеңіту керек. Натурал сандар шектеулі жиындар құратын объектілерді
санаудың нәтижесінде пайда болды деп айтуға болады. Күнделікті жұмыста бір-
бірінен жеке бөлініп тұрған объектілерді ғана санау емес, мәселен, ұзындық,
аудан, көлем, салмақ, уақыт, т.т. сияқты шамаларды өлшеуге тура келеді.
Екінші жағынан натурал сандарға қосу, азайту, көбейту және бөлу амалдарын
жүргізуге тура келеді. Осы айтылған амалдардың жүргізілу нәтижесінде
мынадай қорытындыға келеміз: біріншіден, натурал сандар шексіз, екіншіден,
нөль, теріс және бөлшек сандар сияқты жаңа сандарды енгізіп, сандар ұғымын
кеңітіп толықтыру керек. Қысқасын айтқанда, шамаларды өлшеу проблемасын
санау проблемасына келтіру керек. Ол үшін біз алдымен метр, дециметр,
сантиметр, килограмм, грамм, сағат, минут, секунд сияқты өлшеу бірлігін
еркімізше сайлап аламыз да , сонан соң өлшенетін шамада сайланып алынған
бірлік неше рет болатынын есептейміз. Өлшенетін шамада сайланып алынған
бірлік бүтін сан рет болуы да, болмауы да мүмкін. Жалпы алғанда, сайланып
алынған бірлікпен қандай болсын өлшенетін шама абсолют дәл өлшенбейді, яғни
шама бірлікпен еселі болмайды. Бұл жағдайда бастапқы бірлікті бірдей q
бірлікке бөліп, жаңа өлшеу бірлігін табамыз. Мәселен, бастапқы бірлік 1
метр болса, оны 10-ға бөліп, дециметр бірлігін, жүзге бөліп сантиметр
бөлігін табамыз.
Бастапқы бірлікті тең етіп q бөлікке бөлгеннен шығатын бірлік мынадай
символмен белгіленеді. Егер өлшенетін шама жаңағы бірліктей p есе
болса, онда бұл шаманың өлшемі болады. Мұндай символдарды
математикада бөлшек немесе қатынас деп атайды. Егер p мен q ортақ бөлгіші
жоқ натурал сандар болса, онда символды рационал сан деп атайды.
Барлық оң, теріс, бүтін сандардың, барлық оң, теріс бөлшек сандардың,
нольдің жиынын рационал сандар жиыны деп атайды. Барлық рационал сандар
жиынын былай белгілейді:
R {},
мұндағы p мен q - өзара жай сандар.
Рационал сандарға жүргізілетін амалдар және олардың қасиеттері
оқушыларға белгілі деп есептейміз, дегенмен рационал сандар жиынына тән
келесі қасиеттерді айтып кетуге тура келеді.
1. Егер a мен b берілген түрлі рационал сандар болса, онда бұлардың
арасында мына қатыстар: ab, немесе ab болуы керек, және егер ab, ал
bc болса, онда сөзсіз ac болады. Рационал сандардың мұндай қасиетін
реттілік қасиет дейді.
2. Егер a мен b сандары (ab) берілген түрлі рационал сандар болса,
онда ол екеуінің арасында толып жатұан шексіз көп рационал сандар бар.
Рационал сандардың мұндай қасиетін тығыздық қасиет дейді.
Бұл көрсетілген екі қасиеттен басқа рационал сандар жиыны төмендегі
Архимед аксиомасын қанағаттандырады.
Егер a мен b – кез келген оң рационал сандар болса, онда мына
теңсіздікті nba қанағаттандыратын бүтін n саны әрқашан да табылады.
Рационал сандарды түзудің нүктелерімен кескіндеуге болады. Түзу, оның
кесіндісі, бұл кесіндінің ұзындығы деген мәселелер бізге белгілі деп
ұйғарып, ұшы-қиыры жоқ екі шеті де шексіздікке созылған бір түзуді қарайық.
Осы түзудің жылжымай бір орында тұратын нүктесін алып, оны О әрпімен
белгілейік. Бұл нүктені бас нүкте деп атаймыз. О нүктесінің оң жағында
жатқан түзудің бөлігіне оң бағыт, ал О нүктеснің сол жағындағы бөлігіне
теріс бағыт беретін болып келісейік. Енді ұзындығы бірге тең кесінді
алайық, әдетте мұндай кесіндіні масштаб (өлшем) деп атайды.
В-4 В-3 В-2 В-1 А1 А2 А3 А4
О
Бұдан кейін осы масштабты түзудің бойына О нүктесінен бастап, оңға
және солға қарай өлшеп салайық; сонда мұның нәтижесінде түзу сызықтың
бойында мынадай нүктелер табылады:
А1 , А2 , А3 , А4 , ...
және
В-4 , В-3 , В-2 , В-1 , ...
Бұл шыққан нүктелер мына сандардың
±1, ±2, ±3, ±4, ..., ±n геометриялық кескіні болады.

Вектор ұғымы және оған амалдар
Вектор дегеніміз бағытталған кесінді немесе қайсысы біріншісі (басы А
нүктесі), ал қайсысы екіншісі (соғы В нүктесі) екендігі көрсетіліп берілген
нүктелер жұбы, АВ немесе а символымен белгіленеді. Вектордың модулі немесе
ұзындығы деп, оның басы мен соңының ара қашықтығын айтады. АВ немеса а
символымен белгіленеді. Векторлар бір түзуге параллель болса, онда олар
коллинеар векторлар деп аталады. Векторлар коллинеар болып, бірдей
бағытталған және модульдері тең болса, онда олар тең векторлар деп аталады.
Вектордың модулі бірге тең болса, ол бірлік вектор деп аталады.
Векторлардың біреуін екіншісімен беттескенше бұрғандағы ең кіші айналу
бұрышын сол екі вектордың арасындағы бұрыш деп атайды.
l осіндегі бағытталған А1В1 кесіндісінің шамасы АВ векторының l осіне
проекциясы деп аталып, пр АВ символымен белгіленеді.
а, в, с, векторлары бір жазықтыққа параллель болса, онда олар
компланар векторлар деп аталады.
а векторының λ≠0 санына көбейтіндісі деп, модулі а векторының модулі
мен λ саны модулінің көбейтіндісіне тең, ал бағыты λ0 болғанда, а
векторының бағытымен бағыттас, ал λ0 болса, оған қарама-қарсы бағытта
болатын λа векторын айтады.
Сонда екі вектордың коллинеар болуының қажетті және жеткілікті шарты:
в=λа.
Ал, кез келген а векторын а=а*а-0 түрінде жазуға болады, мұндағы а
вектордың модулі, а-0 бағыты а векторымен бағыттас бірлік вектор.
Үшбұрыш ережесі. а және b векторларының қосындысы деп, басы а =ОА
векторының басымен дәл келетін, ал ұшы а векторынығ ұшына b векторынығ
басы дәл келетіндей етіп салғанда b= АВ векторынығ ұшымен дәл келетіндей с
= ОВ векторын айтады да, с = а+ b деп белгілейді.
Кез келген а және b векторларынығ айырымы деп, b векторына қосқанда а
векторы шығатын с= а-b ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.