Экономикадағы математикалық әдістер мен үлгілер

АЛҒЫСӨЗ
1 ЭКОНОМИКАЛЫҚ.МАТЕМАТИКАЛЫҚ ӘДІСТЕРДІҢ ЭКОНОМИКА
2 МАМАНДЫҚТАРЫ СТУДЕНТТЕРІНІҢ КӘСІБИ БІЛІКТІЛІГІН
ҚАЛЫПТАСТЫРУДАҒЫ АЛАТЫН ОРНЫ
3 Л.В.КАНТОРОВИЧ ЖӘНЕ СЫЗЫҚТЫ ПРОГРАММАЛАУ.
4 ЖҰМЫС БАҒДАРЛАМАСЫ
5 ПӘННІҢ КҮНДЕЛІКТІ . ТАҚЫРЫПТЫҚ ЖОСПАРЫ ЖӘНЕ САҒАТТЫҢ
БӨЛІНУІ
6 ПӘННІҢ ОҚУ.ӘДІСТЕМЕЛІК КАРТАСЫ
7 ТӘЖІРИБЕЛІК САБАҚТАР
8 ОСӨЖ
ӘДЕБИЕТТЕР ТІЗІМІ

1. жолдарды қатарларға ауыстырғанда анықтауыш өзгермейді, яғни транспозициялған матрицаның анықтауышы берілген матрицаның анықтауышына тең.
2. Анықтауыштың екі жолын (қатарын) орнымен ауыстыру оны (-1)-ге көбейтуге теңбе-тең.
3. Егерде анықтауыш екі бірдей жолға (қатарға) ие болса, онда ол нольге тең.
4. Егерде жол (қатар) элементтерінің жалпы көбейткіші болса, онда көбейткішті анықтауыш белгісінің алдына қоюға болады.
5. Егерде бір жолдың (қатардың) сәйкес келетін элементтерін қоссақ, анықтауыш өзгермейді.
Кері матрица

А-ны кез келген матрица деп атайық, сонда В матрицасы кері матрица деп аталады, егерде А*В=В*А=Е, осында Е – бірлік матрица А-1 деп кері матрицаны белгілейміз.
Тек қана квадратты матрица кері матрицаға ие болады. Кері матрицаны табу үшін келесі алгоритмді қолдануға болады:
• Егерде матрица квадратты болса, онда 2 пункке көшеміз, керісінше болса, кері матрица шықпайды.
• А матрицаның анықтауышын шығарамыз, егерде ол нольге тең болса, онда кері матрица шықпайды, керісінше болса, онда 3 пункке көшеміз.
• Матрицаның әрбір элементінің орнына оның алгебралық қосымшасын қоямыз және оны транспозициялаймыз.
• Шыққан матрицаның әрбір элементі берілген матрицаның анықтауышына бөлінеді

1.Акулич И.Л. Математическое программирование в примерах и задачах. М. Высшая школа. 1989.
2. Банди Б.Основы линейного программирования. М. Радио и связь. 1989.
3.Горчаков А.А., Орлова И.В., Половников В.А. Методы экономико-
математического моделирования и прогнозирования в новых условиях
хозяйствовать. М.ВЗФИ. 1991.
4. Исследование операций в экономике (под ред. Н.Ш.Кремера_______) М. Юнити,
1997.
5. Карасев А.И., Кремер Н.Ш., Севельсва Т.И. Математические методы и
модели в планировании. М. Экономика, 1987.
6. Орлова И.В., Половников В.А., Федосеев В.В. Курс лекций по экономико-
математическому моделированию. М.: Экономическое образование, 1993.
7. Статистическое моделирование и прогнозирование./под ред А.Г.Гранберга.
М.Финансы и статис., 1990
8.Экономико-математические методы и прикладные модели Учебно-
методическое пособие / В.А. Половников, И.В. Орлова, А.Н.Гармаш, В.В.
Федосеев. –М.: Финстатинформ. 1997.
9. Оспанов С.С. Экономикадағы сызықтық оптималдылық модельдер. І б.
Алматы, Қазақ университеті, 1999.
10. Үсіпбаева М.Е. Экономикалық-математикалық моделдеу пәнінің есептер
жинағы. Алматы – 1998.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 305 бет
Таңдаулыға:

1-дәріс. Матрица және оның түрлері, қасиеттері, матрицаның
рангісі.Анықтауыштар және оның қасиеттері, алгебралық толықтауыш, минор,
кері матрица.

Анықтама. m – жолдарының және n – қатарларының қиылысындағы элементтерден
тұратын төртбұрышты сан кестесін матрица деп атайды.
Матрицаны А, В, С және т.б. белгілейді.

Мысалы: 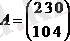- бұл екі жолдан және үш қатардан тұратын матрица. aij – i –
жолының және j – қатарының қиылысында тұратын матрицаның элементі. Мысалы:
3-санды бірінші жол және екінші қатардың қиылысында тұратын элемент.

Анықтама: Егер жолдардың және қатарлардың сандары тең болса, онда матрица
квадраты деп аталады.
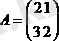- квадратты матрица.
2 1
2 – бас диагоналі. 3 - қосымша диагоналі.

Егер квадратты матрицада бас диагоналінде бір сандары тұрып, ал басқа
элементтері ноль сандары болса, онда ол бірлік матрицасы деп аталады және
она Е деп белгілейді.
Мысалы,

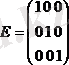
Матрицалармен жасалған амалдар.

1. Матрицалардың санға көбейтіндісі.
Әрбір матрицаны санға көбейтуге болады. Ол үшін матрицаның әр элементін
сол санға көбейту керек.
Мысалы
1.      Матрицалардың қосылуы (алуы).
Әрбір тең екі матрицаны қосуға әлде алуға болады.

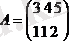
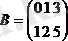
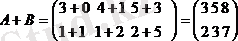
2.      Матрицалардың көбейтіндісі
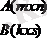
Екі матрица берілген: болғанда ғана болады.
Мысалы,
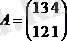
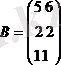
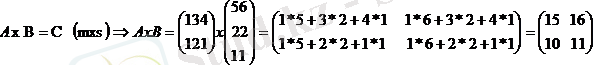4.

Аударылған матрица
жолдармен қатарлардың орындарымен ауыстырылған матрицаны аудару деп
аталады. Олар АТ не А деп белгіленеді.
Мысал

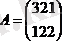
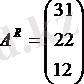
Матрицаның анықтауышы

Анықтама (а11 а22 – а12 а21) саны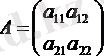квадратты матрицаның анықтауышы деп
аталады.
Анықтауыш 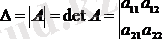белгіленеді.
Мысал

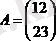
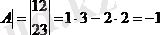
Анықтама кейбір анықтауыштың элементтерінің, жол мен қатарды өшіргеннен
кейін пайда болатын анықтауыш минор деп аталады.

Мәселен, үшінші тәртіптегі анықтауыш қарастырылады:

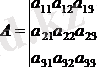
Ендеше, а11 элементінің миноры келесі анықтауыш болады
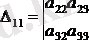
Мысал

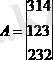
а22 элементінің минорын табу керек

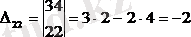
Анықтама Анықтауыштың кейбір элементтерінің алгебралық қосымшасы (-
1)i+j формулаға көбейтілген осы элементтің миноры деп аталады. Яғни i-жол,
j-қатар, осылардың қиылысында тұрған элемент.
Ол 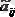арқылы белгіленеді.
Мысал а22 элементінің жоғарыдағы мысалдың алгебралық қосымшасын табамыз.

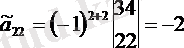
Кез келген өлшемді матрицаның анықтауышы кейбір жолдың қатардың
элементтерімен олардың алгебралық қосымшаларының көбейтіндісінің суммасына
тең.
Мысалы i-жолын белгілейміз. Соның элементтерің алгебралық қосымшаларына
көбейтіп, қосамыз, яғни

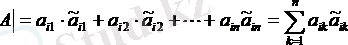
Мысал 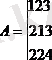бірінші жолмен ыдыратып, топтиаймыз= =

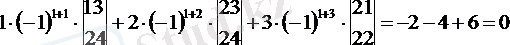
Анықтама үшінші тәртіптегі анықтауышы үшбұрыш ережесі бойынша табуға
болады.
Келесі схемасы бар:

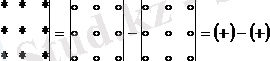
Мысал
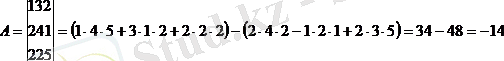
Анықтауыштың қасиеттері:

1.      жолдарды қатарларға ауыстырғанда анықтауыш өзгермейді, яғни
транспозициялған матрицаның анықтауышы берілген матрицаның анықтауышына
тең.
2.      Анықтауыштың екі жолын (қатарын) орнымен ауыстыру оны (-1)-ге
көбейтуге теңбе-тең.
3.      Егерде анықтауыш екі бірдей жолға (қатарға) ие болса, онда ол
нольге тең.
4.      Егерде жол (қатар) элементтерінің жалпы көбейткіші болса, онда
көбейткішті анықтауыш белгісінің алдына қоюға болады.
5.      Егерде бір жолдың (қатардың) сәйкес келетін элементтерін қоссақ,
анықтауыш өзгермейді.

Кері матрица

А-ны кез келген матрица деп атайық, сонда В матрицасы кері матрица деп
аталады, егерде А*В=В*А=Е, осында Е – бірлік матрица А-1 деп кері матрицаны
белгілейміз.
Тек қана квадратты матрица кері матрицаға ие болады. Кері матрицаны табу
үшін келесі алгоритмді қолдануға болады:
•         Егерде матрица квадратты болса, онда 2 пункке көшеміз, керісінше
болса, кері матрица шықпайды.
•         А матрицаның анықтауышын шығарамыз, егерде ол нольге тең болса,
онда кері матрица шықпайды, керісінше болса, онда 3 пункке көшеміз.
•         Матрицаның әрбір элементінің орнына оның алгебралық қосымшасын
қоямыз және оны транспозициялаймыз.
•         Шыққан матрицаның әрбір элементі берілген матрицаның анықтауышына
бөлінеді

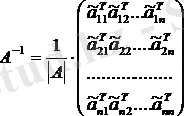
Мысал 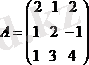А-1 - табу керек

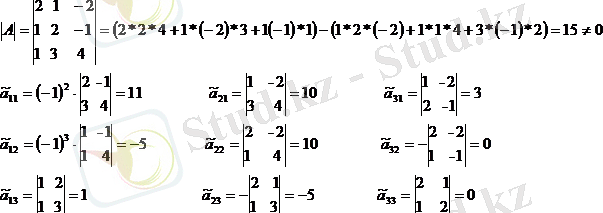
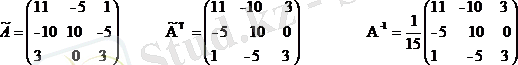
Тексеру

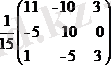
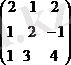
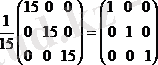
1-дәріс. Матрица және оның түрлері, қасиеттері, матрицаның
рангісі.Анықтауыштар және оның қасиеттері, алгебралық толықтауыш, минор,
кері матрица.

Анықтама. m – жолдарының және n – қатарларының қиылысындағы элементтерден
тұратын төртбұрышты сан кестесін матрица деп атайды.
Матрицаны А, В, С және т.б. белгілейді.

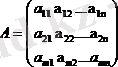
Мысалы: 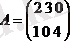- бұл екі жолдан және үш қатардан тұратын матрица. aij – i –
жолының және j – қатарының қиылысында тұратын матрицаның элементі. Мысалы:
3-санды бірінші жол және екінші қатардың қиылысында тұратын элемент.

Анықтама: Егер жолдардың және қатарлардың сандары тең болса, онда матрица
квадраты деп аталады.
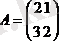- квадратты матрица.
2 1
2 – бас диагоналі. 3 - қосымша диагоналі.

Егер квадратты матрицада бас диагоналінде бір сандары тұрып, ал басқа
элементтері ноль сандары болса, онда ол бірлік матрицасы деп аталады және
она Е деп белгілейді.
Мысалы,

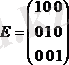
Матрицалармен жасалған амалдар.

1. Матрицалардың санға көбейтіндісі.
Әрбір матрицаны санға көбейтуге болады. Ол үшін матрицаның әр элементін
сол санға көбейту керек.
Мысалы
1.      Матрицалардың қосылуы (алуы).
Әрбір тең екі матрицаны қосуға әлде алуға болады.

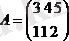
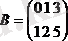
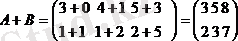
2.      Матрицалардың көбейтіндісі
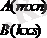
Екі матрица берілген: болғанда ғана болады.
Мысалы,
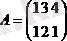
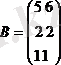
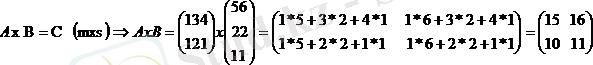4.

Аударылған матрица
жолдармен қатарлардың орындарымен ауыстырылған матрицаны аудару деп
аталады. Олар АТ не А деп белгіленеді.
Мысал

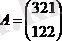
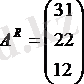
Матрицаның анықтауышы

Анықтама (а11 а22 – а12 а21) саны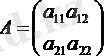квадратты матрицаның анықтауышы деп
аталады.
Анықтауыш 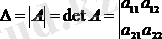белгіленеді.
Мысал

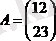
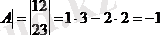
Анықтама кейбір анықтауыштың элементтерінің, жол мен қатарды өшіргеннен
кейін пайда болатын анықтауыш минор деп аталады.

Мәселен, үшінші тәртіптегі анықтауыш қарастырылады:

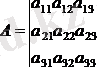
Ендеше, а11 элементінің миноры келесі анықтауыш болады
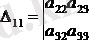
Мысал

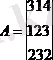
а22 элементінің минорын табу керек

Анықтама Анықтауыштың кейбір элементтерінің алгебралық қосымшасы (-
1)i+j формулаға көбейтілген осы элементтің миноры деп аталады. Яғни i-жол,
j-қатар, осылардың қиылысында тұрған элемент.
Ол 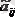арқылы белгіленеді.
Мысал а22 элементінің жоғарыдағы мысалдың алгебралық қосымшасын табамыз.

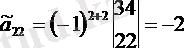
Кез келген өлшемді матрицаның анықтауышы кейбір жолдың қатардың
элементтерімен олардың алгебралық қосымшаларының көбейтіндісінің суммасына
тең.
Мысалы i-жолын белгілейміз. Соның элементтерің алгебралық қосымшаларына
көбейтіп, қосамыз, яғни

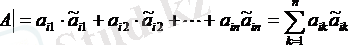
Мысал 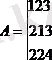бірінші жолмен ыдыратып, топтиаймыз= =

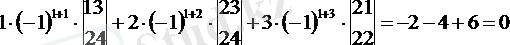
Анықтама үшінші тәртіптегі анықтауышы үшбұрыш ережесі бойынша табуға
болады.

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. ЖҰБАНОВ АТЫНДАҒЫ АҚТӨБЕ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
Ж. Н. Тасмамбетов
ЭКОНОМИКАДАҒЫ
МАТЕМАТИКАЛЫҚ ӘДІСТЕР
МЕН ҮЛГІЛЕР
Оқу құралы
Ақтөбе 2008
2
Қ. Жұбанов атындағы Ақтөбе мемлекеттік университетінің
оқу-әдістемелік кеңесінде мақұлданып, баспаға ұсынылды.
№12 хаттама 5желтоқсан 2008 жыл.
Тасмамбетов Ж.Н.
Экономикадағы математикалық әдістер мен үлгілер. Оқу құралы.
- Ақтөбе: ЖК Жанәділов баспаханасы, 2008 ж. - 262 бет.
Пікір жазғандар:
Тілеубергенов М.І., физика – математика ғылымдарының докторы, профессор.
Асанова А.Т., физика – математика ғылымдарының докторы.
Қабақбаев С.Ж., физика – математика ғылымдарының докторы, профессор.
Оқу құралы университеттің Экономика мамандығы студенттерімен
Экономикалық-математикалық әдістер пәні бойынша дәрістік және
тәжірибелік сабақтарды, өз бетінше жұмыстарды ұйымдастыруға арналған. Пән
бойынша өтуге қажетті Сызықты программалау есебі, оны геометриялық
әдіспен шығару,жасанды базис әдісі, екі жақтылық есебі, көлік қатынасы
есебі
мен салааралық баланс тақырыптарынан теориялық мағлұматтар келтірілген.
Аталған тақырыптар бойынша сызықты үлгілер қарастырылып, оларға қатысты
есептерді шығару жолдары берілген. Жеткілікті көлемде жаттығулар
ұсынылған. Ол студенттермен тәжірибелік сабақтар және өз бетінше
жұмыстарды ұйымдастыруға пайдалы деп есептейміз.
Оқу құралы университеттердің Экономика мамандығы студенттері мен
магистранттарына арналған.
© Тасмамбетов Ж.Н.
3
АЛҒЫСӨЗ
Жоғары экономикалық білімі бар мамандарға қойылатын талаптың бірі
математикалық үлгілеу (молельдеу) әдістерін қолдана білу. Онсыз
экономикалық жүйелер мен үрдістерді (процестерді) талдау мен болжауды
қарастырып, зерттеулер жүргізу мүмкін емес. Математикалық үлгілер
ақпараттарды компьютерлік үлгілеу мен өңдеудің де негізі болып табылады.
Математикалық үлгілердің экономикада қолданылатын ерекшеліктерін көрсету
мақсатында Экономикалық- математикалық үлгілеу термині пайда болды
және университеттің экономика мамандығы студенттеріне Экономикалық-
математикалық әдістер пәні оқытыла бастады.
Экономикада қарастырылатын үлгілер ішінен –сызықты үлгілер ерекше
орын алады. Сызықты үлгілерді зерттеулермен математиканың сызықты
программалау деп аталатын тармағы айналысады.
Сызықты программалау-көп айнымалалардың функцияларының
шартты экстремумдерін табу әдістерін зерттейді. Шартты экстремум ( max
немесе min) табу жолдары Экономикадағы математика пәнін өткен кезде
қарастырылғанмен, қазіргі уақытта ол есептерге басқаша талаптар қойылады.
Атап айтқанда адам өмірінде кездесетін әр түрлі есептердің тиімді
шешімдерін
табуға жете көңіл бөліне бастады. Мысалы, шешімді қандай бір болмасын
жолдармен нақты түрде таңдап алынған параметрлер жиыны деп қарастырсақ,
онда тиімді шешім деп, белгілі- бір байымдаулар бойынша басымдылық
берілген шешімді ұғамыз.
Назарларыңызға ұсынылып отырған оқу құралында сызықты
программалауға келтіретін есептердің сызықты үлгілерін құру жолдары
көрсетіліп, оның тиімді шешімдерін табу үшін қолданылатын әдістер
қарастырылған. Жиі пайдаланылатын графикалық әдіс, симплекс-әдістердің
нақты мысалдары қарастырылып, көптеген есептердің шығарылу жолдары
көрсетілген.Студенттерге есеп шығару жолдарын жеңіл түрде түсіндіру
мақсатында, қарапайым үлгілер қарастырылып, олардың экономикалық
мағыналары көрсетіліп отырылады. Оқулықта Жасанды базистер әдісі ( М-
әдіс), Екі жақтылық есебі, Баланстық әдістер, Серпінді (динамикалық)
үлгілеу
тақырыптарына да жете көңіл бөлінген. Әр тақырыптан соң жетклікті түрде
жаттығулар мен есептер ұсынылады. Өз бетінше қайталау сұрақтары
берілген.Көптеген есептердің шығару жолы, бақылау жұмыстарының орындалу
ерекшеліктері көрсетілген.Өз бетінше жұмыстарды жандандыру мақсатында 10
вариантқа бөлінген тапсырмалар, Рефераттар тақырыптары, емтихан
сұрақтары,тестілік тапсырмалар да берілген. Келтірілген есептер бұрын
тексеруден (апробиация) өткен орыс тілінде шыққан кітаптардан алынды:
1. Сборник задач по математике для экономистов. Под ред. проф. В.И.
Ермакова. Второе издание, исправленное. Москва, ИНФРА-М, 2008,-575 с.
2.Е.В. Шеврина, О.А. Кривцова, Н.В. Спешилова, Л.К. Самойлова. Экономико-
математические модели. Оренбург, 2005, 125 с.
3. В.Л. Никитенков. Задачи линейного программирования и методы их
решения.Сыктывкар, Изд-во СГУ, 2007,-112 с.
4
Соңғы кезде қазақ тіліндегі кітаптардың да қолданысқа ене бастағанын
атап өткен жөн:
1. М.Е. Үсіпбаева. Экономикалық- математикалық модельдеу пәнінің
есептер жинағы.Оқу құралы, Алматы, Республикалық баспа кабинеті,
1998,-86 бет.
2. Ә.Ж. Сапарбаев, Қ:А. Ахметов, А.Т. Мақұлова. Экономикалық-
математикалық әдістер мен модельдер. Алматы, Қазақстан Жоғары оқу
орындарының қауымдастығы, 2005,-400 бет.
3. Оспанов С.А., Асқарова Ж.А. Экономикадағы сызықтық модельдерді
талдаудың математикалық әдістері, жаттығулар мен тәжірибелер, оқу-
әдістемелік құрал, Алматы, НҰР-ПРЕСС,-102 бет.
4. Н.Ш. Альжанова, Х.К. Сәбит. Экономикалық- математикалық әдістер. Оқу
құралы, Алматы, 2007, -44 бет.
5. Беркінбаев К.М., Ажиханов Н.Т., Нұрұллаев А.Н., Ниязова Г.Ж.
Компьютерлік модельдеу негіздері. Алматы, 2007, -71 бет.
Қазақ тіліндегі оқу және оқу-әдістемелік құралдарын пайдаланудағы
кемшілік көптеген терминдер мен түсініктердің бір ізге түспеген әр
түрлілігі. Соған қарамастан келтірілген оқу құралдары студенттерді несиелік
жүйемен оқыту барысында қолданысқа ене бастады. Жоғарыда келтірілген
оқу және оқу-әдістемелік құралдарымен бірге, ұсынылып отырған оқу
құралы да студенттерді несиелік жүйемен оқытып сапалы білім беру
барысында өз орнын табады деген сенімдеміз. Өйткені, орыс тіліндегі
оқулықтардың көптігіне қарамастан университет студенттері мен
магистранттары өз ана тіліндегі оқулықтарға мұқтаж және де келтірілген оқу
құралдарының көбісі несиелік жүйемен оқыту әдістеріне бағытталмаған.
Оқу құралының басында экономикалық- математикалық әдістердің
Экономика мамандықтары студенттерінің кәсіби біліктілігін
қалыптастырудағы алатын орны туралы мақала келтірілген. Онда пәннің
негізі болып саналатын Сызықты программалау есебінің шығу тарихы,
пән бойынша оқылатын тақырыптар мен олардың қолданылу аясы туралы
қысқаша мағлұматтар берілген.
Қысқаша Силлабус пен Жұмыс бағдарламасы оқу құралын
пайдаланушыларға пәнді оқыту мақсаты мен атқаруға тиіс жұмыстары
туралы мәліметтер алуына мүмкіндік береді.Соңғы жағында келтірілген
Практикум, Рефераттар тақырыптары, тестілік тапсырмалар
студенттердің өз бетінше жұмыстары мен зертханалық жұмыстарды
ұйымдастыруға пайдалы деп есептейміз.
5
ЭКОНОМИКАЛЫҚ-МАТЕМАТИКАЛЫҚ ӘДІСТЕРДІҢ ЭКОНОМИКА
МАМАНДЫҚТАРЫ СТУДЕНТТЕРІНІҢ КӘСІБИ БІЛІКТІЛІГІН
ҚАЛЫПТАСТЫРУДАҒЫ АЛАТЫН ОРНЫ
Бүгінгі күні әлемдік деңгейде кең қолданыс тапқан экономикадағы
математика деп аталатын математиканың бөлігі ХХ – шы ғасырдың екінші
жартысында қарқынды дами бастады.
Экономикадағы математика - деген, атауынан көрініп тұрғандай,
математиканың бұл жаңа облысы математикалық әдістердің экономикалық
үрдістерді зерттеуге қолданылуына қатысты. Экономикадағы математиканың
теориясы туралы айтқанда алдымен Ресейдің атақты математигі академик
Леонид Витальевич Канторовичтің (1917-1986) есімі ауызға бірінші ілінеді.
Шынында, оның ашқан сызықты программалау деп аталатын
математиканың тарауы (1939) бүкіл экономика ғылымының бет-пердесін
өзгертті. Әрине, өзі ашқан жаңа бағытты мойындату үшін Л.В.Канторовичке
ұзақ уақыт күресуге тура келді. Оны түсінбеушілік Кеңес экономистері
арасында көбірек болды. Бірақ дүние жүзінде сызықты программалау әдістері
мен идеялары кең көлемде тарап, экономика ғылымы аясынын да шығып,
көптеген пән аралық терең зерттеулерге ұйтқы болды. Сызықты
программалау элементтері өткен ХХ ғасырдың 60 – шы жылдарынан бастап
Қазақстанның жоғарғы мектептерінде, жекелеген түсініктері орта және
арнайы орта оқу орындарында да өткізіле бастады. Ол кезеңді академик Л.В.
Канторовичтің өзі өмір сүріп, қызмет жасаған Кеңестер Одағы кезеңінен
бөліп қарастыра алмаймыз. Сондықтан да, мақаланың бастауын
Л.В.Канторовичтің экономикалық – математикалық теорияның басталуындағы
алатын орнынан бастаймыз.
6
Л. В. Канторович және сызықты программалау
Л. В. Канторович 1912 жылдың 19 қаңтарында Санкт-Петербург
қаласында дәрігерлер жанұясында дүниеге келді. 1926 жылы 14 жасында, ол
Ленинград университетіне оқуға түседі. Сол кездегі Ленинград
университетінде
қалыптасқан жақсы математикалық орта бар болатын. Көп ұзамай
Л.В.Канторович студенттерге арналған белгілі математик Г. М. Фихтенгольцтің
жетекшілігімен ұйымдастырылған үйірмеге қатыса бастайды. Профессор Г.
М. Фихтенгольцтің Математикалық талдау курсына арналған оқулықтары
осы күнге дейін жоғары оқу орындарында қолданыс табуда. 1930 жылы ЛМУ
–ді бітірген ол, Ленинградтың оқу орындарында сабақ бере жүріп ғылыми
зерттеулермен де айналысады. Ғылыми зерттеулерінде үлкен жетістіктерге
жетіп, 1932 жылы Ленинградтың азаматтық құрылыс инженерлерін дайындау
институтында профессор атағын, ал 1934 жылы ЛМУ профессорлығын
алады.Өзі қатысқан Г. М. Фихтенгольцтің математикалық үйірмесі
Л.В.Канторович- Фихтенгольцтардың ғылыми семинарына айналады. Ол
математиканың көптеген салаларынан жаңалық ашқан белгілі ғалым ретінде
танылады. Өз өмірінде 300 – ден астам ғылыми еңбектер жазған ғалым,
еңбектерін мынадай тоғыз тарауға жіктеп қарастыруды ұсынады [1]:
1) функцияның дескритивті теориясы және жиындар теориясы,
2) функцияның конструктивті теориясы,
3) талдаудың жуықтау әдістері,
4) функциональдық талдау,
5) функциональдық талдау және қолданбалы математика,
6) сызықты программалау,
7) есептеуіш техника және программалау,
8) тиімді жоспарлау және тиімді бағалар,
9) жоспарлы экономиканың экономикалық проблемалары.
Бастапқы тараулар 1) –4) көбірек теорияға жақын болса, соңғы 5) –9)
тараулары қолданбалы жағына жақынырақ. Бірақ, өзі атап көрсеткендей
ғылымның өзінде іштей бірлік бар, математика мен экономиканың жан – жақты
7
теориялық және қолданбалы проблемаларын шешуге қажетті идеялар мен
өзгерістердің бір–біріне бойлай енуі орын алады. Оның шығармашылығына
тән ерекшелік сол кездегі математика мен экономиканың ең ауыр
проблемалары мен болашаққа бағытталған алдыңғы қатарлы идеяларының
өзара байланыстылығы. Сондай проблемалардың бірі сызықты программалау
есебі. Кезінде - өміріңіздегі ең маңызды ғылыми жетістігіңіз не деп
есептейсіз
деген сұраққа - ол сызықты программалау деп, жауап берген. Сызықты
программалаудың пайда болу тарихы мен оның байланыстарына қысқаша
тоқталайық.
Сызықты программалау.Күнделікті өмірде әр түрлі шешімдер ішінен,
мүмкін болатын ең дұрыс шешімді таңдап алуға тура келеді. Оны тиімді
шешім – деп те атайды. Мұнда біз қолда бар құралдар мен қорлардың әр
уақытта жеткілікті бола бермейтінін ескеруіміз керек. Аз мүмкіндіктерді
пайдалана отырып, үлкен жетістіктерге жету үшін жоспар, немесе
әрекеттердің бағдарламасын құру қажет. Оны ғылыми тұрғыдан тиянақтау
үшін XX – шы ғасырдың орта шенінде арнайы математикалық аппарат
құрылды. Математиканың бұл тарауы математикалық программалау деп
аталды. Мұндағы прогаммалау сөзін ЭЕМ- да программа құрумен шатастырмау
керек. Ол кейін пайда болған сызықты программалау, серпінді
программалау т.с.с. түсініктер мен ұштасып жатыр. Сызықты программалау
пайда болған уақыты 1939 жылы Л.В. Канторовичтің “Өндірісті ұйымдастыру
мен жоспарлаудың математикалық әдістері” атты кітабының шыққан
уақытымен байланыстырылады. Канторовичтің келтірген математикалық
әдістері қолмен есептеуге жарамсыз болды, ал тез есептейтін қазіргі заманғы
есептеуіш машиналар жоқ болды. Сондықтан оның жұмыстары біршама уақыт
ескерусіз қалды. Екінші жағынан Канторовичтің экономикаға қатысты бұл
еңбегі көптеген ғалымдар жағынан түсінік таппай, оған жалған ғылым сияқты
көзқарас қалыптасты. Канторовичке экономикадағы математиканы қолдану
бағытындағы жұмыстарын уақытша тоқтата тұруға тура келді.
8
Сызықты программалаудың өмірге қайта келуін 1950 – ші жылдардың бас
кезінде ЭЕМ- ның пайда болып, жедел қолданысқа енгізілумен байланыстыруға
болады. Леонид Витальевичтің концепциясы соғыстан кейінгі жылдары қайта
ашылды. Америкалық экономист Т. Купманс біршама жылдар бойы математик
ғалымдардың назарын әскери тақырыптарға қатысты ұшақтардың ұшу кестесін
құру, қорларды таратып орналастыру т.б. проблемаларға аударды. Нәтижесінде
математикалық ұжым құрылып, көп-жақтардағы сызықты теңсіздіктермен
берілген сызықты функциялардың экстремумын табу есептерін қарастыра
бастады. Математиканың бұл тармағы Т. Купманстың ұсынысымен (1951ж)
сызықты программалау деп аталды. Кейін операцияны зерттеу,
математикалық экономика, экономикалық кибернетика сияқты аттармен
белгілі болып, тарала бастаған сызықты программалау-сызықты тиімділік
үлгілерін зерттеуге, яғни тиімді мәндері табылуы қажет есептерді шығаруға,
теориялық және сандық талдаулар жүргізуге арналған. Мұндағы үлгілер
зерттелетін объектілер мен үрдістердің, құбылыстардың ең маңызды жақтарын,
белгілерін көрсетуге мүмкіндік береді. Тиімділік немесе экстремум мәндер
табу – максимум немесе минимум мәндер табу. Зерттелетін үрдіс қандай бір
болмасын теңсіздіктер жүйесімен сипатталады.
АҚШ- та сызықты программалау 1947 жылдан бастап, Дж Данциг -–
еңбектерінде қалыптаса бастады. Ол, кейін симплекс әдіс деген атақ алған
сызықты программалау есептерін шығарудың қолдануға жеңіл, сандық әдісін
ойлап тапты. Қойылған кедергілерге қарамастан Л.В. Канторович та
экономикалық идеяларға құрылған математикалық жұмыстарына қайта
оралып, Д.Ж.Данцигтен тәуелсіз симплекс әдістің идеясына келді. Оның бұл
еңбектерін жоғары бағалаған Д.Ж.Данциг Канторович өндіріске қатысты
есептердің үлкен , маңызды класын математикалық тұрғыдан сипаттауға көз
жеткізген бірінші адам болды. Оның ойынша бұлай сипаттау есепке сандық
тұрғыдан қарауға және оны сандық әдістермен шығаруға мүмкіндік
береді...Канторович алғашқы табылған мүмкін шешімді пайдалануға
9
негізделген әдісті сипаттады... -деп, өзінің сызықты программалаудың
тарихына арналған еңбегінде атап өтті.
Л.В.Канторовичтің экономикалық жаңалығын қысқаша -тиімді шешім
мен тиімді бағаның өзара тәуелділігі деп тұжырымдауға болады.
Леонид Витальевич 1957 жылғы Ғылым Академиясының Сібір бөліміне
жұмысқа ауысады. Осы кезден бастап ол экономикалық немесе онымен
байланысты математикалық проблемалармен айналысып, бұрынғы жасалған
жұмыстарын ашық түрде жалғастыруға мүмкіндік алды. Бұрын
жарияланбаған еңбектері де жарық көре бастады. Оның ішінде Қорларды
пайдаланудың ең жақсы экономикалық есептеулері кітабы да бар.Осы
жасалған еңбектері Кеңестер Одағында В.В. Новожилов және В.С.
Немчиновтармен бірге 1965 жылы Лениндікпен сыйлықпен , ал 1975 жылы
М Купманспен бірге Нобель сыйлықтарымен марапатталады.
Сызықты программалау идеяларының қарышты дамып, қолданысқа ене
басталғаны соншалық, қазір экономика мамандығын алған кез келген
студентке таныс. Ол Қазақстанның университеттерінде оқытылып жүрген
Экономикалық- математикалық әдістер пәнімен тікелей байланысты.
Өтілетін негізгі:
1.Сызықты программалауға келтіретін өндіріске қатысты есептер.
Сызықты модельдер.
2. Сызықты программалау есебінің жалпы қойылуы. Дөңес көпжақтар
және сызықты теңсіздіктер.
3.Симплекс әдістің теориясы.
4.Екі жақтылық симплекс әдіс.
5.Сызықты программалаудың арнайы есептері. Көлік қатынасы есебі.
Көлік қатынасы есебінің потенциалдар әдісі.
6. Салааралық баланс.
сияқты тақырыптар экономист мамандарға математиканың экономикада
қолданылу мүмкіндіктерінің кең екендігін көрсетіп, нарықты экономикада
тиімді жоспарлар құрып, оның шешімдерін нақты табуға мүмкіндік
10
жасайтынын көреміз. Пәннің атынан байқалғандай экономикалық -
математикалық ағартуға, нәтижесінде экономика – математикалық
мәдениет түсінігін қалыптастыруға келеміз. Мұндағы математика
фундаменталь және қолданбалы зерттеулердің негізі болып табылады.
Сондықтанда математикалық пәндер Математика мен Информатика
мамандықтары студенттерінің ғана кәсіби біліктілігін қалыптастыруға ғана
емес, сонымен қатар Экономика мамандығы студенттерінің де кәсіби
біліктілігін қалыптастыру үшін өте маңызды.
Экономика мамандығында оқитыны студенттердің экономикалық
мәдениеті I-II курстарда өтетін Экономикалық теория, Экономикалық
ғылымдар тарихы, Экономикалық білімдер негіздері,
Макроэкономика, Микроэкономика сияқты пәндер өтуі кезінде
қалыптасады. Онда көптеген экономикалық үрдістердің үлгілері түсініктерімен
танысады. әр түрлі деңгейдегі тапсырмалар алып, есептер шығарады. Тәжірибе
көрсеткендей осы пәндерден көптеген түсініктер жете түсінбей қабылданады.
өйткені, ЭМӘ (экономикалық- математикалық әдістер) пәнінің басқа пәндердің
арасындағы алатын орны туралы әлі зерттеулер жүргізіліп, оған деген жаңа
көзқарас Қазақстан Республикасының оқу орнындарында қалыптасқан жоқ.
Мұнда бірнеше мәселелерге түбегейлі көңіл бөлу керек деп есептейміз.
1. Пән аралық байланыстар. Әсіресе “Экономика” мамандығы
студенттеріне оқылатын: Экономикадағы математика, Информатика,
Эконометрика, Ықтималдық теориясы мен статистика- пәндері.
Болашақ мамандардың математикалық мәдениетін қалыптастыру
“Экономикадағы математика” пәнінен басталады. Математикалық аппарат
– экономикалық талдау ұйымдастыру және басқарудың маңызды құралы.
Сондықтан да, оны оқылатын математиканың түсініктерінде экономика, қаржы,
басқаруға қатысты қолданбалары жағына көңіл аударылып отыру керек. Осы
жерде математиканы оқытудағы қолданбалы бағыт түсінігіне келеміз.
Көптеген зерттеушілер қолданбалы бағытты жүзеге асырудың негізгі құралы
есептер екенін атап өтеді [2]. Ал, экономикалық мазмұнды есептер
11
математикалық аппарат қолданылатын қолданбалы есептердің маңызды түріне
жатады.
Нақты объектілер өте күрделі, сондықтан да оларды зерттеу үшін,
зерттелетін нақты оъектінің көшірмесі, яғни үлгісі құрылады. Үлгі неғұрлым
сәтті таңдап алынып, құрылған болса, соғұрлым нақты объекті туралы дәл
ақпарат алуға, мүмкіндік береді.
Ғылыми зерттеулерде натурал, физикалық, абстрактілі және
математикалық сияқты үлгілер жиі пайдалынады. Математикалық үлгілер құру
– математикалық үлгілеу деп аталады. Математикалық үлгілерді пайдалану
арқылы математика ғылыми зерттеулерде, ғылымның барлық салаларында,
оның ішінде экономика ғылымы да бар қолданыла бастады. Ақпарат, объект,
жүйе, алгоритм, формальдау және үлгілеу, программа түсініктері
Информатика пәнінің негізгі маңызды түсініктері болып табылады [3].
Бұдан үлгілеудің негізгі қалыптасуы Информатика пәнінде екендігін көруге
болады. Жоғарыда келтірілгендей ЭЕМ дамуы экономикадағы тиімділік
есептерінің шешімдерін табуда маңызды роль атқарды. Сол сияқты
“Экономика” және “Ықтималдық теориясы мен статистика ” пәндерінің
байланыстарына да тоқталуға болады. Олардың бәрі де сызықты программалау
есептерін терең талдауға мүмкіндік береді.
2. ЭМӘ пәнінің өзінде өтетін тақырыптардың нақтылануы, яғни болашақ
мамандардың экономика – математикалық мәдениетін қалыптастыруға қатысты
тақырыптардың бір жүйеге келтірілуі және әр тақырыптар бойынша мақсаттар
қоя білу:
- Сызықты программалаудың тиімділік есептерінің математикалық
үлгілерінің жіктемелерін білу;
- Сызықты программалаудың тиімділік есептерінің математикалық үлгілерін
құруды игеру;
- Сызықты программалау есебін (СПЕ) канондық түрге келтіруді игеру;
- СПЕ – ні векторлық түрде жазуды игеру;
12
- СПЕ – ні n=3, n=2, k≤ 2 мәндері үшін прафикалық әдіспен шығаруды
меңгеру;
- СПЕ шығару үшін симплекс - әдісті қолдануды меңгеру;
- Жасанды базистер әдісін қолдануды біліп, оны бастапқы бұрыштық
нүктені табуға қолдануды меңгеру;
- Сызықты программалаудың бастапқы есебіне екіжақтылық есебін құруды
игеру;
- Минимум мән туралы 1- ші және 2 – ші теоремаларды айта біліп, оны
СПЕ шығаруға қолдана білу;
- Екі жақтылық симплекс - әдістің қолданылу ерекшеліктерін меңгеру;
- СПЕ шығарудың кері матрица әдісін меңгеру;
- Көлік қатынасы үлгісі негізінде сызықты программалаудың арнайы
есептері туралы мағлұматы болу;
- Балансқа келтірілген және келтірілмеген көлік қатынасы үлгілерінің
шығарылу ерекшеліктерін білу;
- Солтүстік - батыс бұрышы әдісін көлік қатынасы есебіне қолдана білу;
- Фогель әдісін көлік қатынасы есебіне қолдануды игеру;
- көлік қатынасы есебінің тиімді жоспарын табуға потенциялдар әдісін
колдануды игеру;
- көлік қатынасы үлгілеріне келтірілетін экономикалық есептер туралы
мағлұматы болу ( тағайындау есебінің мысалы негізінде);
Бұл тақырыптарды Баланстық үлгілер тақырыбына қатысты түсініктер
толықтырады:
- салааралық баланстың жалпы сұлбасын және оның негізгі төрт
ширектерінің мазмұндарын білу;
- тура және толық материальдық шығындар коэффициентерін есептей білу;
- тура және толық еңбек сыйымдылығы коэффициентерін, қор
сыйымдылығы коэффициентерін есептей білу;
3. Қарастырылатын тақырыптарды олардың шығу тарихымен байланыстырып
өту. Шынында, тиімділік есептері немесе экстремаль есептердің мыңдаған
13
жылдық тарихы бар [4]. Ал экономикадағы тиімділік есептерімен өткен
ғасырдың орта шенінде жаппай айналыса бастады. Соның бір мысалы,
Канторовичтің оқушыларымен бірге құрған жеңіл машиналармен жолаушылар
тасудың математикалық үлгісі. Оны пайдалану нәтижесінде тасымалдаумен
айналысудың тиімділігі артты. әсіресе қысқа қашықтыққа тасымал жасаудың
тиімділігі артатыны дәлелденді.
Сондай – ақ көлік қатынасы есебі де, бұрынғы Кеңестер Одағында
алғашқы қолданыс тапқан есептердің бірі. Мысалы, 1959 жылы Москваның 8
өзен порттарына жүк тасымалданатын 209 тұтынушыларын бекітіп, тиімді
жоспар құру нәтижесі мықты экономикалық жетістіктерге қол жеткізген.
Көптеген есептердің шығарылып дамуына олардың әскер істерінде
пайдаланылуы себепші болған т.с.с.
4. Экономикалық мазмұнды есептерді шығаруға компьютерлік техниканы
пайдалануға жете көңіл бөлу. Мұнда екі жақты пайдалылық бар. Біріншіден,
студенттердің компьютерлік технологияны пайдалану дағдысы артады да,
өздерінің болашақ мамандықтарына пайдалану ерекшеліктерін қалыптастыра
береді. Екіншіден, айнымалылар саны көп, көп параметрлі экономикалық
есептердің үлгілерін қарастыру арқылы студенттерге сызықты программалауда
қолданылатын экономика – математика әдістерін жете түсіндіруге мүмкіндік
туындайды. Қоданбалы бағыттағы есептерді көптеп шығарып салыстыруға
мүмкіндік алады.
5. Мектеп математика курсында тиімділік есептерінің алатын орнын анықтау.
Бұл бағытта Ресейде бұрынғы Кеңес дәуірінен бастап жүргізіліп келе жатырған
академик В.М. Монахов пен оның ғылыми педагогикалық мектебінің
еңбектерін атауға болады. Мұнда сызықты программалаудың кәзіргі нарықты
экономикадағы орнын аша түсетін Ойындар теориясы ,
Операцияларды зерттеу сияқты курстармен байланыстары да ұзақ
жылдардан бері жете зерттеліп келеді. Педагогикалық институттардың
математика және информатика мамандығы студентеріне аталған курстардың
оқытылу әдістемелерін зерттеп, экономика – математикалық әдістерді
14
пайдалану мадениетін қалыптастыру мектеп математика курсында алған
білімдерін де пайдалану ерекшеліктері қарастырылуда [2].
Қысқаша мақалада сызықты программалаудың математиканың функциональ
және дөңес талдаулар, дискретті математикамен, вариациялық есептеулер және
Лагранжа көбейткіштерімен, ықтималдық теориясы, Марков процестері,
жуықтап есепетеулермен т.б. байланыстары қарастырылмай қалды. Жоғарыда
айтылғандардан, бастауын 1938 жылы Л.В. Канторовичке фанер тресінің
қойған ресурстарды тиімді пайдалану есебінен алған сызықты
программалаудың немесе экономикадағы математиканың XX ғасырдағы
ғылым тарихының жарқын беттерінің бірі және математиканың ажырамас
бөлігі екенін көреміз. Ол Қазақстанның математика және экономика
ғылымдарында өз орнын табуда.
Әдебиеттер.
1. Масштабы творчества Наука в Сибири, № 1 (2337), 11 января 2002г.
2. В. М. Монахов, С.М. Населький, Д.А. Власов. Экономическая культура –
обязательный компонент профессиональной компетентности учителя
математики Школьные технологии. № 6, 2002, с. 32 – 57.
3. Тасмамбетов Ж.Н., Тасмамбетова А.Ж. Информатиканың негізгі
түсініктерін қалыптастыру. Гуманитарлық зерттеу мәселелері, № 1,
Ақтөбе, 2006, 66 – 68 б.
4. Тихомиров В. М. Рассказы о максимумах и минимумах. М., Наука, 1986,
190 с.
15
Экономикалық –математикалық модельдеу курсы бойынша SYLLABUS
050506- Экономика мамандығына арналған
2 кредит, 5-семестр 2008-2009 оқу жылы
Оқытушылар: профессор Жақсылық Нұрадинұлы Тасмамбетов
Байланыс телефоны 21-27-24
Ғимараты: №5 оқу корпусы, Ы. Алтынсарин көшесі, №4 үй
Аудиториялар мен сабақ уақыты: сабақ кестесі бойынша
Оқытылу мерзімі: 2 ауысым
Сабақ саны: дәріс – 1 сағат
практикалық сабақ – 1 сағат
ОСӨЖ – 1 сағат
Алдын-ала қойылатын талаптар:
Математика пәнінен білімдар болуы керек:
0 Сызықты алгебра;
1. Аналитикалық геометрия элементтері;
2. Математикалық анализ;
3. Ықтималдық теориясының элементтері;
Экономикалық пәндер циклынан білімдар болуы керек:
0 микроэкономика;
2. макроэкономика;
3. менеджмент және маркетинг.
Курстың мақсаты: Нарықтық экономика кезіндегі өндірісті басқаруға қатысты
есептерін шешуге және талдауға экономика-математикалық әдістерді қолдану,
оның теориялық және методологиялық проблемаларын, принциптері мен
қойылу әдістемелерін баяндау.
Курстың ____________сипаттамасы: Пәнді оқу, өндіріс қызметін нарықты
экономика
кезінде басқаруға байланысты өтетін экономикалық құбылыстар мен
процестерді математикалық моделдеудің әдістерінен мағылұмат береді.
Студент экономикалық моделдерді шешудің математикалық әдістерін,
тәжірибелік дағдыларын меңгеруі тиіс. Әртүрлі математикалық түсініктер мен
алгоритмдердің экономикалық интерпретациясын білуі, тиімді шешімдер
әдістерін меңгеруі қажет.
Курсты өтіп болғаннан кейінгі білім және дағды қалыптасу.
Курсты өткен студент мыналарды білуі қажет.
• Өндірісті жоспарлау есібінің қойылуын және ЭММ-ін, құрылғылардың
қуаттарын тиімді пайдалана білулері қажет.
• Экономикалық есептерді графикалық әдістермен шығара білуі;
• Бағаларды біртіндеп дәлдеу әдісінің алгоритмін білу және есептерді
симплекс-кестені пайдаланып шығара білу;
• Аралас шектеулермен берілген сызықты программалау есебіне М әдісті
пайдалана білу.
• Екі жақтылық есебінің қойылуын және математикалық жолмен шығару
алгоритмін білу.
16
• Көлік қатынасы есебінің қойылуы мен ЭММ-ін білу. Бірінші тіректі
жоспарды солтүстік-батыс бұрышы ең кіші элемент және Фогель
әдістерімен таба білу. Потенциалдар әдісін пайдаланып, көлік қатынасы
есебінің тиімді жоспарын табу.
• Салааралық баланс моделдерінде тура, жанама және толық материалдық
шығындар коэффициенттерін анықтай білу.
• Жаппай қызмет көрсету моделінің негізгі компоненттерін білу, шешім
қабылдай білу.
• Ойындар теориясының ЭММ-ін құра білу. Ноль қосындылы екі адамның
ойынын құра білу.
Негізгі әдебиеттер тізімі.
1.Акулич И.Л. Математическое программирование в примерах и задачах. М.
Высшая школа. 1986.
2. Банди Б.Основы линейного программирования. М. Радио и связь. 1989.
3.Горчаков А.А., Орлова И.В., Половников В.А. Методы экономико-
математического моделирования и прогнозирования в новых условиях
хозяйствовать. М.ВЗФИ. 1991.
4. Исследование операций в экономике (под ред. Н.Ш.Кремера_______) М.
Юнити,
1997.
5. Карасев А.И., Кремер Н.Ш., Севельсва Т.И. Математические методы и
модели в планировании. М. Экономика, 1987.
6. Орлова И.В., Половников В.А., Федосеев В.В. Курс лекций по экономико-
математическому моделированию. М.: Экономическое образование, 1993.
7. Статистическое моделирование и прогнозирование.под ред А.Г.Гранберга.
М.Финансы и статис., 1990
8.Экономико-математические методы и прикладные модели Учебно-
методическое пособие В.А. Половников, И.В. Орлова, А.Н.Гармаш, В.В.
Федосеев. –М.: Финстатинформ. 1997.
9. Оспанов С.С. Экономикадағы сызықтық оптималдылық модельдер. І б.
Алматы, Қазақ университеті, 1999.
10. Үсіпбаева М.Е. Экономикалық-математикалық моделдеу пәнінің есептер
жинағы. Алматы – 1998.
Курстың жоспары
№ Тақырыбы дәріс
1 ЭММ-нің негізгі түсініктері. ЭМ-лық өндірістік есептердің
қойылуы.
1
2 Сызықты бағдарлау есебінің (СБЕ-нің) жалпы қойылу қысқаша
жазылуы. Канондық форма.
1
3 СБЕ-нің геометриялық интерпретациясы. Екі айнымалы
жағдай үшін сызықты форманың қасиеті.
1
4 СБЕ есептерін графиктік шешу. Мысалдар. 1
5 Тіректі жоспарды біртіндеп жетілдіру алгебрасы (Сиплекс -
әдіс). Базистік айнымалылар.
1
17
6 Бастапқы жоспарды іздеуді стандартты жазу. 1
7 Симплекс кестелердегі бағалауды біртіндеп дәлелдеу әдісінің
алгоритмі.
1
8 Тиімді жоспар жаңа кестесіне көшу. Мысал. 1
9 Жасанды айнымалылар. Бастапқы тіректі жоспарды құрудың
жасанды базистер әдісі.
1
10 СБЕ-ін шығарудың аралас шектеулермен берілген М әдісі. 1
11 М әдісінің тиімді жоспары. Мысал. 1
12 Бағалауды біртіндеп дәлдеу әдісі. Бағалауды біртіндеп
дәлелдеу әдісінің алгоритмі.
1
13 Мүмкін –екі жақты кестелер. Мысал. 1
14 Сызықты бағдарлаудың екіжақтылық есебі. Екі жақтылықтың
негізгі теоремасы.
1
15 Екі жақтылық моделінің экономикалық мағынасы. Мысал. 1
16 Көлік қатынасы моделін құру. Теңестірілген және
теңестірілмеген көлік қатынасы моделдері.
1
17 Көлік қатынасы кестесі. Тасымалдаудың алғашқы жоспарын
анықтау (Солтүстік – батыс бұрышы әдісі, ең кіші тариф әдісі).
1
18 Алғашқы жоспарды іздеудің Фогель әдісі. Көлік қатынасы
есебінің туындыланған және туындыланбаған жоспары.
1
19 Жанама және нақты шығын. Қайтадан есептеудің айырымды
циклдары.
1
20 Потенциалдар әдісінің алгоритмі. Мысал. 1
21 Көлік қатынасыесебінің тиімді жоспары. 1
22 Баланстық әдіс. Салааралық баланстың принципті схемасы. 1
23 Салааралық баланстың экономика-математикалық әдістері. 1
24 Тура және жанама материалдық шығындардың
коэффициенттері.
1
25 Өндірістің сала аралық балансы кестесін құру және өнімді
таратудың экономикалық мысалын үш салалы бойынша
көрсету.
1
26 Жалпы қызмет көрсету жүйесінің қолданылу аясы. Жалпы
қызмет көрсету жүйесінің жүктемесі.
1
27 Талап қоюдың Пуассон ағыны және оның қасиеттері. Тұйық
және тұйық емес жүйелер. Жүйе көрсеткіштерінің есептелу
алгоритмдері.
1
28 Эрланг формуласы. Сипаттарды есептеу мысалдары. 1
29 Жанжалды жағдайлар. Ойынның әртүрлі түрлері. Ойындар
теориясының қолданылу аясы. Төлемдік матрица.
1
30 Ерше нүкте стратегиясы. Ойындар теориясының мысалдары. 1
БАРЛЫҒЫ 30
18
Курсқа қойылатын талаптар:
Қажет әдебиеттер мен құралдар.
• ЭММ пәні бойынша оқулықтар.
• Дәрістер жинағы
• Калькулятор, сызғыш, қалапсаптар.
Курстың саясаты мен процедурасы.
ОСӨЖ – зертханалық жұмыс тақылеттес өз бетінше орындалатын жеке жұмыс.
Жалпы бағалау жүйесі.
Қорытынды баға мына көрсеткіштерден жинақталады:
Сабаққа қатысу. Студенттің сабаққа қатысуы міндетті. Әлдеқандай
себептермен сабақ жіберген жағдайда, ол жіберілген сабақты міндетті түрде
өтеуі (отработка) тиіс. Егер студент сабақтардың 50% себепсіз жіберсе, онда
емтихан тапсыруға жіберілмейді.
Үй тапсырмасы. Әрбір ОСӨЖ сабағында үй тапсырмасы қабылданады. Үй
тапсырмасы белгіленген уақыттан кейін аз балмен бағаланып қабылданады.
Барлық алдын-ала орындалған үй тапсырмаларына семестр соңында 8 балл
қосылады.
Семестрлік тапсырмалар. Семестрлік тапсырмалар студенттің семестр
бойынша өз бетінше шығаруына арналған. Оны тапсыру және қорғау
белгіленген график бойынша жүргізіледі. Семестрлік тапсырмалар кешігіп
орындалған жағдайда қабылданбайды.
Коллоквиум. Өтілген материалдар бойынша семестр бойына жазбаша немесе
ауызша түрде бір еет өткізіледі. Мерзімі және қабылдау түрі оқу процесінің
графигінде көрсетіледі.
Бақылау тестілері. Бақылау тестілері семестр бойына еет ке сәйкес үш
еет өткізіледі. Бақылау тестісі ашық немесе жабық формада өткізілетін
аралық бақылау түрі.
Емтихан: Семестрдің соңында емтихан өткізіледі, емтиханның мерзімі
деканаттың кестесімен белгіленеді. Емтихан компьютерлік тест түрінде
өткізіледі. Тестке курстағы программа бөліктерінің тапсырмалары енгізіледі,
емтиханда дәріс конспектісін, оқулықты, кез-келген жазбаны қолдануға
болмайды. Емтихан ережесін сақтамаған студент, емтиханнан босатылады және
емтихан тапсырмаған болып есептелінеді.
19
Бағалар шкаласы:
Баға Балл Проценттер Дәстүрлі жүйе бойынша
баға
A 4,0 100%
А- 3,67 90 – 94%
өте жақсы
B+ 3,33 85 – 89%
B 3,0 80 – 84%
B- 2,67 75 – 79%
Жақсы
C+ 2,33 70 – 74%
C 2,0 65 – 69%
C- 1,67 60 – 64%
D+ 1,33 55 – 59%
D 1,0 50 – 54%
Қанағаттанарлық,
орташа
F 0 0 – 49% Қанағаттанарлықсыз
РЕЙТИНГІК БАҒАЛАУ
АПТАЛАР
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Балл
Сабаққа
қатысу
0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,2 0,2 0,2 0,2 0,2 4
Дәріс
конспектісі
2 2 4
Практикалық
сабақ
1 1 1 1 1 1 1 1 1 1 1 1 1
13
Үйге
тапсырма
1 1 1 1 1 5
ОСӨЖ 2 2 2 2 8
Бақылау
жұмысы
2 3 2 3 10
Тест 1 2 1 2 6
Коллоквиум 5 5
Семестрлік
тапсырма
5 5
Семестр
бойынша
60
Қорытынды
емтихан
40
Барлық
баллдар
100
Негізгі талаптар:
1. Студент сабақ кестесіне қойылған барлық сабаққа қатысуға міндетті.
Алдын-ала келісім бойынша жіберген сабақтарын өтеуі қажет. Егер
жіберген сабақтарын өтемесе емтиханға жіберілмейді.
20
2. Кез келген себеппен сабаққа 2 рет кешіксе, ол 1 рет сабаққа қатыспаған
болып есептеледі және сабаққа қатысымы үшін қойылатын ұпай саны
төмендетіледі.
3. Барлық тапсырмаларды орнатылған мерзімінде тапсыру.
Курсты жүргізу.
1. Аудиториялық сабаққа дәріс, практикалық сабақ, ОСӨЖ, материалды
талдау, әртүрлі тапсырмалар мен жаттығуларды орындау уақыттары енеді.
Әрбір сабаққа студент дайындықпен келуі керек.
2. Әрбір дәрістік сабақта негізгі түсініктер мен анықтамалар беріледі.
Студент сабаққа қатысуға және дәрісті жазуға міндетті. Қатыспаған
жағдайда басқа студенттен көшіріп алу керек. Оқытушы әр студент үшін жеке
дәрістік материал бермейді.
3. Практикалық сабақта студентке практикалық жұмыстардың сипатттамасы
беріледі және тақырып бойынша өз бетінше орындайтын тапсырма беріледі.
Егер студент тапсырманы орындап үлгермесе, оны студенттің үйде
орындауына рұқсат етіледі. Ол үшін студент тапсырманы дискетке көшіріп
алып, келесі сабақта оқытушыға тапсыруы керек. Бұндай жағдай 3 реттен
артық рұқсат етілмейді.
4. Егер студентке бір нәрсе түсініксіз болса, міндетті түрде оқытушыдан
сұрауы керек.
5. Үй тапсырмасын орындағанда студентке компьютер пайдалану тиімді.
6. Компьютер кабинетіне кіру оқытушы немесе оператордың рұқсатымен ғана
жүзеге асады және сабақ кестесінен тыс компьютер кабинетінде жұмыс жасау
оператордың қатысуымен ғана орындалады.
7. Сабақтан немесе сабақ кезінде орынсыз сұрануға рұқсат етілмейді.
8. Сабақ барысында ұялы телефонмен сөйлесуге, бөгде жұмыстармен
айналысуға қатаң түрде тыйым салынады.
Емтихан сұрақтары
№ Тақырыбы
1 ЭММ-нің негізгі түсініктері. ЭМ-лық өндірістік есептердің қойылуы.
2 Сызықты бағдарлау есебінің (СБЕ-нің) жалпы қойылу қысқаша жазылуы.
Канондық форма.
3 СБЕ-нің геометриялық интерпретациясы. Екі айнымалы жағдай үшін
сызықты форманың қасиеті.
4 СБЕ есептерін графиктік шешу. Мысалдар.
5 Тіректі жоспарды біртіндеп жетілдіру алгебрасы (Сиплекс - әдіс). Базистік
айнымалылар.
6 Бастапқы жоспарды іздеуді стандартты жазу.
7 Симплекс кестелердегі бағалауды біртіндеп дәлелдеу әдісінің алгоритмі.
8 Тиімді жоспар жаңа кестесіне көшу. Мысал.
9 Жасанды айнымалылар. Бастапқы тіректі жоспарды құрудың жасанды
базистер әдісі.
10 СБЕ-ін шығарудың аралас шектеулермен берілген М әдісі.
21
11 М әдісінің тиімді жоспары. Мысал.
12 Бағалауды біртіндеп дәлдеу әдісі. Бағалауды біртіндеп дәлелдеу әдісінің
алгоритмі.
13 Мүмкін –екі жақты кестелер. Мысал.
14 Сызықты бағдарлаудың екіжақтылық есебі. Екі жақтылықтың негізгі
теоремасы.
15 Екі жақтылық моделінің экономикалық мағынасы. Мысал.
16 Көлік қатынасы моделін құру. Теңестірілген және теңестірілмеген көлік
қатынасы моделдері.
17 Көлік қатынасы кестесі. Тасымалдаудың алғашқы жоспарын анықтау
(Солтүстік – батыс бұрышы әдісі, ең кіші тариф әдісі).
18 Алғашқы жоспарды іздеудің Фогель әдісі. Көлік қатынасы есебінің
туындыланған және туындыланбаған жоспары.
20 Потенциалдар әдісінің алгоритмі. Мысал. Көлік қатынасыесебінің тиімді
жоспары.
22 Баланстық әдіс. Салааралық баланстың принципті схемасы.
23 Салааралық баланстың экономика-математикалық әдістері.
24 Тура және жанама материалдық шығындардың коэффициенттері.
25 Өндірістің сала аралық балансы кестесін құру және өнімді таратудың
экономикалық мысалын үш салалы бойынша көрсету.
26 Жалпы қызмет көрсету жүйесінің қолданылу аясы. Жалпы қызмет көрсету
жүйесінің жүктемесі.
27 Талап қоюдың Пуассон ағыны және оның қасиеттері. Тұйық және тұйық
емес жүйелер. Жүйе көрсеткіштерінің есептелу алгоритмдері.
Жоғарыда келтірілген қысқаша Силлабус несиелік оқу жүйесінде
студенттердің өзіндік жұмысын ұтымды ұйымдастыруға бағытталған және
пәнді оқитын барлық студенттерге таратылады. Онда студенттерге қойылатын
негізгі талаптар көрсетілген. Ол талаптармен студенттер топтарға бекітілген
эдвайзерлер арқылы толығымен әрбір семестр басында таныстырылады.Кейбір
мамандықтарға арнайы курс ретінде басқаша атаумен ЭКОНОМИКАЛЫҚ
ПРОЦЕСТЕРДІ МОДЕЛЬДЕУ ЖӘНЕ БОЛЖАУ пәні де ұсынылып
жүр.Төменде кафедрада пайдаланып жүрген ЖҰМЫС БАҒДАРЛАМАСЫ-да
келтірілген.
22
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
Қ.Жұбанов атындағы Ақтөбе мемлекеттік университеті
БЕКІТЕМІН
Экономика факультетінің деканы
__________ Жүнісов Б.А.
қолы
______________________ 2008 ж.
ЖҰМЫС БАҒДАРЛАМАСЫ
1. Мамандық атауы және шифры: 050506- Экономика_______________
2. Білім беру деңгейі жоғары базалық білім (бакалавр)_______________
3. Оқыту нысаны: Орта білім негізіндегі күндізгі оқу
4. Пән атауы және коды (Оқу жоспарына сәйкес): _________________________
____ЭКОНОМИКАЛЫҚ-МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ _
Пәнді оқытатын кафедра (атауы, индексі): 07.10-05 Жоғары математика және
қолданбалы информатикa________________________ __________________
Оқу жылы: 2008-2009, Семестр: 5
5. 7. Оқу процесінің жоспарына сәйкес, пәнді оқытуға бөлінген сағат саны:
аудиториялық сабақ 40 сағат, оның ішінде:
дәріс - ___15 сағат__
практика - ___15 сағат__
ОСӨЖ - ___10 сағат__
Өзіндік жұмыс - __50 сағат
Барлық сағат саны: __90 сағат
8. Оқу жоспарында қарастырылған бақылау жұмыстарының саны –
9. Қорытынды бақылау нысаны – емтихан
10. Іздеу үлгісі(негізгі ұғымдар): мақсат функциясы, шектеу жүйелері,
алғашқы
жоспар, тиімді жоспар, симплекс-әдісі, таяныш жоспарын біртіндеп жақсарту
әдісі. Потенциалдар әдісі,
қосалқылық_________________________ ___________________
23
I ЖҰМЫС БАҒДАРЛАМАСЫ ДАЙЫНДАЛЫП ЕНГІЗІЛГЕН
Орындаушылар
ЖМ және ҚИ кафедрасының профессоры ________________ Тасмамбетов
Ж.Н.
_________________2008ж
Орындаушылар
Жауапты орындаушы – кафедра меңгерушісі
п.ғ.к., _____________ Әбдібекова С.Қ.
қолы
_________________2008ж
II КАФЕДРА ОТЫРЫСЫНДА ТАЛҚЫЛАНДЫ
хаттама № ___1____ ___ _______ 2008 ж.
III СЫН - ПІКІР БЕРУШІ
Алгебра және дифференциалдық теңдеулер
кафедрасының меңгерушісі, ф.-м.ғ.к. ________________ Шерияздан. Т.Т.
қолы аты-жөні
_______________2008 ж.
IV ФАКУЛЬТЕТТІҢ ӘДІСТЕМЕЛІК КОМИССИЯСЫНА БЕКІТУГЕ
ҰСЫНЫЛДЫ
хаттама № __1__ ___ _________ 2008 ж.
V АЛҒАШҚЫ ТЕКСЕРУ МЕРЗІМІ 2009__ жыл
ТЕКСЕРУ МЕРЗІМДІЛІГІ 1 жыл
VI АУЫСТЫРУҒА ЕНГІЗІЛДІ __________ _____________________
Алдыңғы Жұмыс бағдарламасының
бекітілген күні
24
11. Пәнді оқытудың негізгі мақсаты: Пәнді оқу, өндіріс қызметін нарықты
экономика кезінде басқаруға байланысты өтетін экономикалық
құбылыстар мен процестерді математикалық моделдеу арқылы
мағылұмат ету; әртүрлі математикалық түсініктер мен алгоритмдердің
экономикалық интерпретациясын білу, тиімді шешімдер әдістерін
меңгеру; студенттердің экономикалық моделдерді шешуде математикалық
әдістерін, тәжірибелік дағдыларын қалыптастыру.
12. Студент пәнді оқу нәтижесінде игеруге тиісті негізгі
сипаттамалар,білім, дағды және білік:
Курсты өткен студент мыналарды білуі қажет.
• Өндірісті жоспарлау есібінің қойылуын және ЭММ-ін, құрылғылардың
қуаттарын тиімді пайдалана білулері қажет;
• Экономикалық есептерді графикалық әдістермен шығара білуі;
• Бағаларды біртіндеп дәлдеу әдісінің алгоритмін білу және есептерді
симплекс-кестені пайдаланып шығара білу;
• Аралас шектеулермен берілген сызықты программалау есебіне М әдісті
пайдалана білу;
• Екі жақтылық есебінің қойылуын және математикалық жолмен шығару
алгоритмін білу;
• Көлік қатынасы есебінің қойылуы мен ЭММ-ін білу. Бірінші тіректі
жоспарды солтүстік-батыс бұрышы ең кіші элемент және Фогель
әдістерімен таба білу. Потенциалдар әдісін пайдаланып, көлік қатынасы
есебінің тиімді жоспарын табу;
• Салааралық баланс моделдерінде тура, жанама және толық материалдық
шығындар коэффициенттерін анықтай білу;
• Жаппай қызмет көрсету моделінің негізгі компоненттерін білу, шешім
қабылдай білу;
• Ойындар теориясының ЭММ-ін құра білу. Ноль қосындылы екі адамның
ойынын құра білу.
Курсты өткен студент келесі даңдыларды игеруі қажет:
• Әртүрлі экономикалық моделдерді құруға іс жүзінде машықтану;
• Модельдерді шешуге қажетті математикалық түсініктер мен құралдарды
жете меңгеру;
• Оптималды шешімдерді талдаудың негізгі әдістерін қолдана білу;
• Алынған тиімді жоспарға экономикалық талдау жасауды іс жүзінде
меңгеру және сәйкес шешім қабылдау;
• Әдістердің алгоритмдерін және қолданбалы программалар пакеттерін
қолдана білу.
25
13. Пәннің күнделікті – тақырыптық жоспары және сағаттың бөлінуі
№ Дәрістердің
тақырыптары
Дәріс Практика
лық сабақ
ОСӨЖ СӨЖ Бағалау
формасы
1. Өндірісті жоспарлау
есебінің қойлымы және
ЭММ. Сызықты
программалау есебінің
жалпы түрі. Сызықты
программалау есебінің
стандартты, канондық
түрлері.
1 1 - 2 Диалог
2. Сызықты программалау
есебінің геометриялық
интерпретациясы.
Сызықты программалау
есебін шығарудағы
графиктік тәсіл.
1 1 1 3 Блиц-сұрау
3. Таяныш жоспарын
біртіндеп жақсарту
әдісінің (ТЖБЖ)
алгебрасы. Симплекстік
кестелердегі әдістің
алгоритмі.
1 2 1 5 Диалог
4. М-әдісі. М-есебінің
тиімді шешімдеріне
байланысты
теоремалар.
2 1 1 5 Диалог
5. Айныған шешім ұғымы.
Бағаларды біртіндеп
жақсарту әдісі.
(қосалқы симплекс
әдісі).
1 1 1 5 Бақылаужұм
ысы
6. Қосалқылық есебінің
қойлымы және
экономикалық
мағынасы. Қосалқы
есеп моделін құру
алгоритмі.
1 2 1 5 Блиц- сұрау
7. Біртекті жүктерді
тасымалдау есебінің
қойлымы және
экономикалық
мағынасы. Алғашқы
2 1 1 5 Диалог
26
таяныш жоспарын құру
әдістері.
8. Потенциялдар әдісі. 1 2 1 5 Блиц- сұрау
9. Баланстық моделдер. 2 2 1 5 сұрау
10. Көпшілікке қызмет
көрсету жүйелері
моделдерінің негізгі
құрауыштары.
2 1 1 5 Бақылаужұм
ысы
11. Ойындар теориясы. 1 1 1 5 сұрау
Барлығы: 15 15 10 50
14. Пәннің оқу-әдістемелік картасы:
Дәріс
№ Сабақ
тың №
Сабақтың жоспары, негізгі дидактикалық
бірліктер
Ағымдық
бақылау түрі
1 1 ЭММ-нің негізгі түсініктері. ЭМ-лық өндірістік
есептердің қойылуы. Сызықты бағдарлау
есебінің (СБЕ-нің) жалпы қойылу қысқаша
жазылуы. Канондық форма.
1 2 СБЕ-нің геометриялық интерпретациясы. Екі
айнымалы жағдай үшін сызықты форманың
қасиеті. СБЕ есептерін графиктік шешу.
Мысалдар.
Диалог
2 3 Тіректі жоспарды біртіндеп жетілдіру
алгебрасы (Сиплекс - әдіс). Базистік
айнымалылар. Бастапқы жоспарды іздеуді
стандартты ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.