Үш еселі интегралдың қолданылуы

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті

«Математика» кафедрасы

Курстық жұмыс

Тақырыбы: Үш еселі интегралдың қолданылуы

Орындаған: Балташ У

Ғылыми жетекші:Назарова. К

Түркістан 2012

Мазмұны

Кіріспе . . . 3

Тарау Үш еселі интеграл

1. 1. Үш еселі интегралдың анықтамасы . . . 4

1. 2. Үш еселі интегралдың қасиеттері . . . 5

1. 3. Үш еселі интегралды есептеу . . . 7

1. 4. Үш еселі интегралдың қолданулары . . . 9

1. 5. Кейбір механикалық және физикалық есептерге қолдану . . . 11

1. 6. Кеңістіктегі полярлық координаттар(сфералық координаттар) . . . 13

Қорытынды . . . 16

Пайдаланылған әдебиеттер . . . 17

Кіріспе

Интеграл(лат. іnteger - бүтін) -математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.

Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. 9 - 15-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Тек 16 - 17-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. «Интегралдық есептеу» термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты. 19-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есептеуді дамытуға 19-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафнутий Чебышев үлкен үлес қосты. Жалпы үш еселі интеграл дененің көлемін есептеу

және пайдалану жолдары, физикалық және механикалық қолданулары қарастырылады.

Тарау Үш еселі интеграл

1. 1 Үш еселі интегралдың анықтамасы.

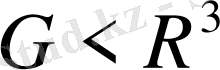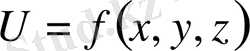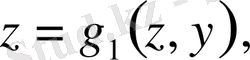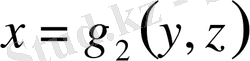Үш өлшемді жабық облысында үздіксіз функциясы берілсе, сол облысын шектеп тұрған бетті деп, ол туралы теңдеуі не , не 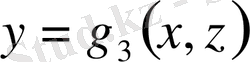болатындай бөліктерден тұрады деп болжаймыз. Енді облысын қалауымызша 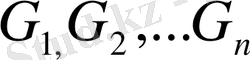деген бөліктерге бөліп, олардың көлемдерін сәйкес 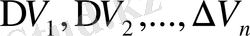десек. Әрбір жекелеген бөліктен қалауымызша бір нүкте алып, 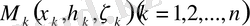деп белгілейік. Содан соң берілген функциясының мәндерін алынған нүктелерде есептеп, мынадай қосынды түзелік:

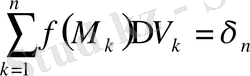(1. 1. 1)

Осы 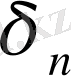қосындысын функция 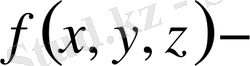тің үш өлшемді интегралдық қсындысы деп атаймыз.

Анықтама. Егер бөліктердің 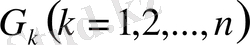ең үлкен диаметрі 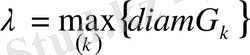нольге ұмтылғанда интегралдық қосынды 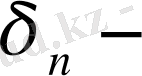нің шегі бар болып және ол облысын майда бөліктерге бөлу тәсілінен де, әр бөліктегі 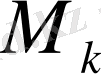нүктесін таңдауға да тәуелсіз болса, ол шек облысындағы берілген 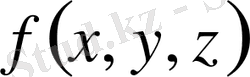функциясының үш еселі интегралы деп аталынады да былай жазылады:

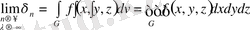(1. 1. 2)

Бұл жағдайда функциясы облысында интегралданатын делінеді.

1. 2 Үш еселі интегралдың қасиеттері.

Екі еселі интеграл қасиеттеріне ұқсас үш еселі интеграл қасиеттерін атап өтейік:

1-қасиет. Егер кез-келген тұрақты, ал 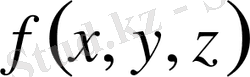фунциясы облысында интегралданса 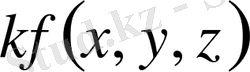көбейтіндісі де интегралданады және

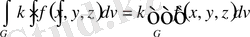
теңдігі орындалады.

2-қасиет. Егер облысында 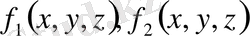функциялары жеке-жеке интегралданса, олардың алгебралық қосындысы де интегралданады және мына теңдік орындалады:

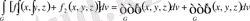
3-қасиет. Егерде 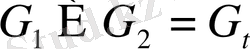болып, функция 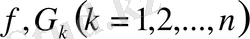облысында интегралданса және 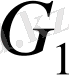мен облысының ортақ ішкі нүктелері болмаса мына теңдік

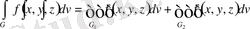
орындалады.

4-қасиет. G облысында f(x, y, z) пен функцияларының әрқайсысы интегралданатын болып, сонымен қатар облыста арақатыс

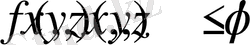
орындалса, олардың үш еселі интегралдары үшін арақатыс

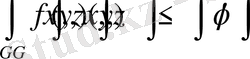
орындалады.

5-қасиет . Егер G облысында интегралданатын функция f(x, y, z) таңбасын өзгертпесе, сол таңба үш еселі

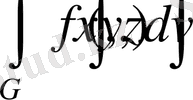
интегралында сақталады.

6-қасиет. Егер f (x, y, z) функциясы G облысында интегралданса, оның абсолют шамасы 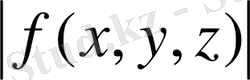сол облыста интегралданады және

болады.

7-қасиет. G обыснда интегралданатын функция f (x, y, z) сол облыста 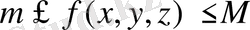орындалса, онда

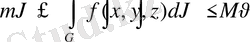
8-қасиет. Егер f (x, y, z) функциясы жабық және шектелген G облысында үзіліссіз болса бұл облыста 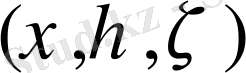нүктесі табылып, үш еселі интеграл шамасы 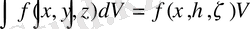теңдігімен анықталады.

1. 3 Үш еселі интегралды есептеу.

Біз үш еселі интеграл

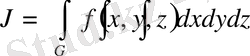(1. 3. 1)

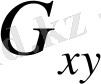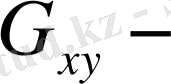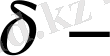-ді есептеу керек делік. Мұндағы облысы бетінен шектеліп, оның жазықтығындағы проекциясы қарапайым қисықпен шектелген дұрыс облысть болса, ал тің ішкі нүктесінен осіне парапллель түзу бетін тек екі нүктеден ғана кесіп өтетін болса (1-сызба) облысын үстіңгі жағынан шектеп тұрған беттің теңдеуі , ал ның блысын төменгі жағынан шектеп тұрған бөлігінің теңдеуін 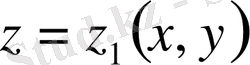десек, сонда екі еселі интегралдағыдай қайталама интегралдар қарастырсақ

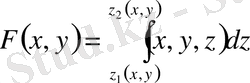
Бұдан мына теңдікті аламыз:

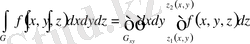(2. 3. 2)

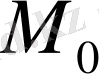
Мұндағы G облысындағы бойынша үш еселі интегралды қайталама интегралддардың біреуімен жазсақ, онда

аламыз.

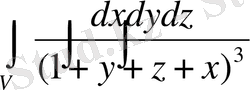
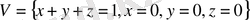Мысал.

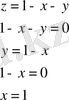
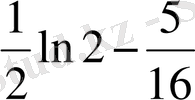
Жауабы:

1. 4 Үш еселі интегралдың қолданулары.

1. Дененің көлемі. Бізге 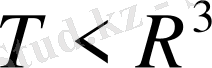облысы берілді делік, үш еселі интегралдың анықтамасына сай, сол облыстың көлемі 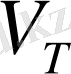былайша есептеледі:

(1. 4. 1)

Егер 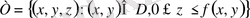болса, ал облысы 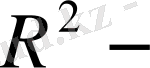де 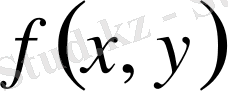фукциясы сол облыста үздіксіз болса, онда үш еселі интеграл (1) -ті қайталама интегралға келтіріп,

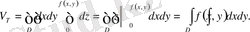
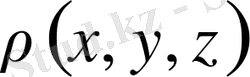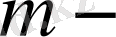2. Егер көлемнің тығыздығы үш аргументтің үзіліссіз функциясы болатын денесінің массасы ді табу керек десек, ол үшін үш еселі интегралмен былайша есептеледі

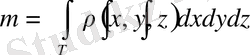(1. 4. 2)

1. 5 Кейбір механикалық және физикалық есептерге қолдану .

Тығыздығы функциясы арқылы берілген материалдық дене үшін мына формула орын алады:

1) Дененің координаталық жазықтықтар арқылы статикалық моменттері

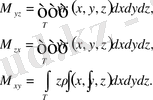
2) дененің ауырлық центрінің координаталары

3) Координаталық жазықтықтар арқылы дененің инерциялық моменттері

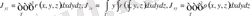
4) Координаталық осьтер арқылы дененің инерциялық моменттері

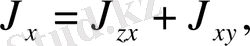
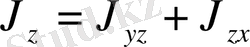
5) Координаталар төбесі арқылы дененің инерциялық моменті

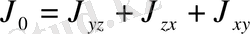
6) Дененің тартылу өрісінің Ньютондық потенциалы ( 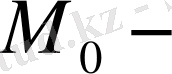нүктесінде)

Мұндағы

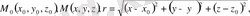
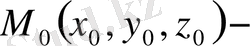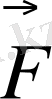
7) Массасы болатын материалдық нүкте дің денесіне тартылу күші 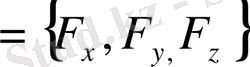десек,

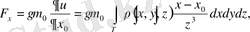
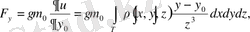
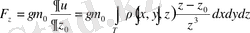
болады.

1. 6. Кеңістіктегі полярлық координаттар

(сфералық координаттар) .

Үш еселі интегралды есептеу үшін кейбір жағдайларда

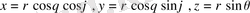(1. 7. 1)

түріндегі айнымалдар ауыстыруы арқылы 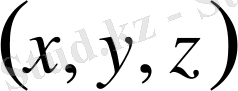декарат координаттарынан 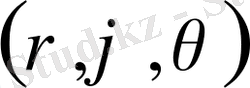сфералық кординаттарына өту тиімді (3-сызба) .

Мұнда:

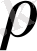арқылы 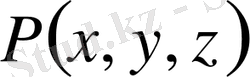нүктесінен координат басына дейінгі қашықтық;

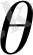арқылы 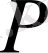радиус- векторы мен оның 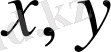жазықтығындағы проекциясының арасындағы бұрыш;

арқылы осы проекция мен 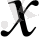өсінің оң бағыты арасындағы бұрыш белгіленген.

Соңғы екі бұрыштың өзгеру аралықтары:

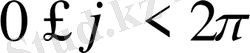және

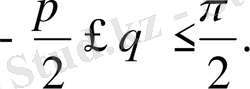
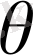
(1. 7. 1) түрлендірудегі якобиан

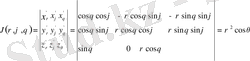
Сонымен 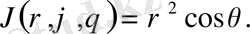Олай болса сфералық координаттар үшін (9) формула келесі түрден жазылады:

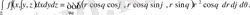
(1. 7. 2)

Сфералық координаттар мысалына жер бетінің георафиялық координаттары (бойлық (долгота) пен ендік (широта), - жер центріне дейінгі қашықтық) жатады.

Цилиндірлік координаттар. Үш өлшемді кеңістіке 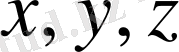тік бұрышты координаттар жүйесі берілсін. Кеңістіктің кез келген 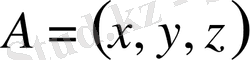нүктесін 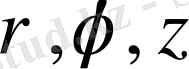сандар үштігімен де анықтауға болады (5-сызба) . Мұндағы нүктенің бұрынғы апликатасы, ал 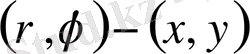жазықтығындағы нүктенің полярлық координаттары (поляр өсі оң