Механика логикасы

Жоспар
Кіріспе

І ӘР ТҮРЛІ САНАҚ ЖҮЙЕЛЕРІНДЕ КИНЕМАТИКАНЫҢ ЕСЕПТЕРІН ШЕШУ
1.1 Бірқалыпты.айнымалы қозғалыс
1.2 Айнымалы қозғалыс
1.3 Қозғалыстың тәуелсіздік принциптері
1.4 Есептерді шығарудың координаттық әдісі
1.5 Импульстің сақталу заңы
1.6 Энергияның сақталу заңы
1.7 Тербелістер

Негізгі есеп: кез келген уақыт мезетінде дененің орнын табу.
Ол үшін: координата жүйесі мен санақ жүйесін таңдау, орын ауыстыруды анықтау қажет болады, ол үшін жылдамдықты, үдеуді және уақытты білу керек.
Қозғалыстардың сипаты Ньютон заңдарымен анықталады. Күшті анықтау үшін оның координатаға (ауырлық, серпімділік) немесе жылдамдыққа тәуелділігін білу керек.
Импульстің сақталу заңы әсерлесетін денелердің жылдамдықтары арасындағы қатынасты анықтауға мүмкіндік береді.
Энергияның сақталу заңы координата мен дененің жылдамдығы арасындағы байланысты бекітеді.
Негізгі түсініктер: материалдық нүкте, санақ жүйесі, жол, орын ауыстыру, орташа және лездік жылдамдық, үдеу, масса, күш, импульс, жұмыс, потенциальдық және кинетикалық энергия; амплитуда, период, жиілік, фаза.
Заңдар:: Галилейдің салыстырмалылық принципі, Ньютон заңдары, бүкіләлемдік тартылыс заңы, Гук заңы, импультің және энергияның сақталу заңдары.
Негізгі түсініктер мен заңдарға шолу жасау үшін материалдық нүктенің негізгі сипаттамаларының кестесін қолданайық. Осы кестеден есептерді шығару тәсілдерін де алуға болады – қандай параметрлер өзгерді және осы өзгерістерді көрсететін теңдіктерді жазу:

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:

Механика логикасы
Негізгі есеп: кез келген уақыт мезетінде дененің орнын табу.
Ол үшін: координата жүйесі мен санақ жүйесін таңдау, орын ауыстыруды
анықтау қажет болады, ол үшін жылдамдықты, үдеуді және уақытты білу керек.
Қозғалыстардың сипаты Ньютон заңдарымен анықталады. Күшті анықтау үшін
оның координатаға (ауырлық, серпімділік) немесе жылдамдыққа тәуелділігін
білу керек.
Импульстің сақталу заңы әсерлесетін денелердің жылдамдықтары арасындағы
қатынасты анықтауға мүмкіндік береді.
Энергияның сақталу заңы координата мен дененің жылдамдығы арасындағы
байланысты бекітеді.
Негізгі түсініктер: материалдық нүкте, санақ жүйесі, жол, орын
ауыстыру, орташа және лездік жылдамдық, үдеу, масса, күш, импульс, жұмыс,
потенциальдық және кинетикалық энергия; амплитуда, период, жиілік, фаза.
Заңдар:: Галилейдің салыстырмалылық принципі, Ньютон заңдары,
бүкіләлемдік тартылыс заңы, Гук заңы, импультің және энергияның сақталу
заңдары.
Негізгі түсініктер мен заңдарға шолу жасау үшін материалдық нүктенің
негізгі сипаттамаларының кестесін қолданайық. Осы кестеден есептерді
шығару тәсілдерін де алуға болады – қандай параметрлер өзгерді және осы
өзгерістерді көрсететін теңдіктерді жазу:

Идеал күй параметрлері
күй
объект
теңдеуі
Координаталар орын ауыстыру r =
r0 + v0t+
жол
S = v0t +
материальдық жылдамдық орташа v
= или v =
нүкте
лездік V = dV dt

үдеу толық
а =
нормаль
a = или a = w2R
әсерлесу күш гравитациялық
F=

үйкеліс F = kN

серпімділік F = -kx
масса инерциялық
m = m0
гравитациялық
m =
импульс
P = m × V

энергия кинетикалық
K =
потенциальдық
П = П = mgh

Салыстырмалылық принципі – физикадағы іргелі принциптердің бірі

Дене (немесе денелер), басқа дене қозғалысымен салыстырғанда,
қозғалмайтын болып саналатын дене санақ денесі деп аталдады.
Координаталар жүйесі және сағат санақ жүйесін құрайды. Мектептегі
физика курсында тек қана координаталардың тікбұрышты декарттық жүйесі
қоланылады. Бірақ ол жалғыз ғана жүйе емес, теориялық зерттеулерде үнемі
цилиндрлік, сфералық, полярлық және басқа да координата жүйелерін
қолданады.
Механикалық қозғалыс дегеніміз уақыт өтуімен бір дене басқа
қозғалмайтын денелермен салыстырғанда орын ауыстыруының өзгерісі.
Кез келген тең уақыт аралығында бірдей жол жүретін дене қозғалысын –
бірқалыпты қозғалыс деп атаймыз.
Бір қалыпты қозғалып келе жатқан әр түрлі денелер бірдей уақыт
аралығында әр түрлі жол жүруі мүмкін.
Бірлік уақыт мөлшерінде қозғалып келе жатқан дене қанша жол жүретінін
көрсететін физикалық шама – жылдамдық деп аталады.
Жылдамдық санақ жүйесіне тәуелді. Мысалы:
Екі автомобиль 45 кмсағ және 50 кмсағ жылдамдықпен түзу сызықты тас
жолда жүріп келеді. Бірінші автомобильдің екіншімен салыстырғанда
жылдамдығы қандай, егер:
а) олар қарама-қарсы жүріп келе жатса;
б) бір бағытта қозғалса.
Бірінші жағдайда жылдамдық 95 кмсағ, ал екіншіде – 5 кмсағ тең
болады.
Галилейдің салыстырмалылық принципі: бір қалыпты түзу сызықты
қозғалысты ешқандай механикалық тәжірибелерден көру мүмкін емес.
Әр түрлі санақ жүйелеріндегі құбылыстарды сипаттай білу білімін дамыту
үшін бірнеше мысалдар қарастырайық..
1. Кеменің үстінде тұрған жолаушыға салыстырмалы және жағадағы
балықшыға салыстырмалы жүзіп келе жатқан кеме желкенінің ағашынан
құлаған доптың траекториясы қандай? (түзу, парабола).
2. Жылқыға мінген цирк жонглері допты лақтырып, қағып алады.
Көрермендерге және жылқыға қатысты доптың ұшу траекториясы қандай
болады? Ойын алаңы және жылқы санақ жүйелерінде доптың орын
ауыстыруы мен жүрген жолы бірдей бола ма? (парабола, түзу; ойын
алаңына қатысты орын ауыстыру мен жүрген жол көп болады).
3. Жаяу жүруші 60 кмсағ жылдамдықпен қозғала ала ма? (ия, мысалы,
жүріп келе жатқан автомобильге қатысты).
ӘР ТҮРЛІ САНАҚ ЖҮЙЕЛЕРІНДЕ КИНЕМАТИКАНЫҢ ЕСЕПТЕРІН ШЕШУ

1 мысал. Көпір астында жүзіп келе жатқан балықшы қармағын түсіріп алды.
Ол оны 10 мин кейін байқады да, кері бұрылып, қармағын көпірден шақырымға
төмен жерден қуып жетті. Балықшы өзен бойында төмен және жоғары бірдей
ескенін ескере, өзен ағысының жылдамдығын анықтау қажет.
“Жер” санақ жүйесінде бұл есеп былай
В А шешілуі мүмкін:
С

Ағынға қарсы балықшы Vқ – Vө жылдамдықпен АВ жол жүреді, демек

Ағынмен ВС аралықты Vқ+Vө жылдамдықпен жүзіп өтеді, барлық уақытта ол
АС ара қашықтықты жүзіп өтті

Сонымен қатар, суреттен көретініміз . ВС, АВ және АС мәндерін қоя,
жақшаларды аша, табамыз
,
және теңдіктен Vө анықтаймыз.
Қармақ санақ жүйесінде су қозғалмайды және қайық тұрған суда 10 минут
жүзеді, содан кейін тұрған судағы бақылаушы қайтадан қайтып келеді. Демек,
қозғалыс уақыты екі жаққа да бірдей болу керек. Яғни қайықты біз 20 минут
немесе 1,5 сағат бақыладық. Осы уақытта көпір 1 шақырымға (км) жылжиды,
сондықтан, қозғалыс жылдамдығы 3 кмсағ тең.
2 мысал. 1200 метрге созылған, моторландырылған әскерлер легі 18 кмсағ
жылдамдықпен қозғалады. Лектің алғы қатарындағы командир лектің соңына
жерге қатысты екі жаққа да 72 кмсағ жылдамдықпен қозғалған мотоциклшіні
тапсырмамен жібереді. Тапсырманы орындағаннан кейін мотоциклші қанша
уақытта қайтады?

Y

B1 B2 B3 A1
A2 A3 X

СЖ жер - мотоциклші А1 нүктесінен шықты. Оның қозғалысы кезінде лектің
соңы В1 нүктесінен В2 нүктесіне орын ауыстырса, яғни мотоциклші
(1)
жүріп өтеді.
Лектің жүрген уақытында мотоциклшіге кері қайтқанда лектің В2А2
ұзындығын және А2А3 ара қашықтығын өту керек болды, яғни
(2)
(1)-ден

және (2)-ден
,
табамыз

t = 1200м(20мс +5мс)+1200м(20мс–5мс)=128 с
СЖ лек - мотоциклші екі жаққа да бірдей L ара қашықтықты жүріп өтеді,
бірақ оның қозғалысының жылдамдығы бір жаққа және екінші жаққа .
Бірден t1 және t2 мәндерін аламыз.

Өз бетімен шығаруға арналған есептер
1. Ұзындығы L кеме көлде бірқалыпты және түзісызықты қозғалады. Қайық
кеменің артқы жағынан кеменің тұмсығына дейін және кері t уақытта
өтеді. Егер қайықтың жылдамдығы суға қатысты Vқ болса, кеменің
қозғалыс жылдамдығын табу керек. ().
2. Теңізде бірқалыпты қозғалып келе жатқан теплоходтың жылдамдығын және
жел жоқ деп есептегенде ауадағы дыбыстың жылдамдығын анықтау керек.
Егер кеменің ортасынан шыққан дыбыс дабылы кеменің тұмсығына 0,103 с
кейін, ал кеменің артына 0,097 с кейін жетсе. Теплоходтың ұзындығы 68
м. (340 мс).
3. Ағысқа қарсы жүзіп келе жатқан қайық өзен бойында аққан салды
кездестіреді. Бір сағаттан кейін қайықтың моторы өшіп қалады. Моторды
жөндеу 30 минутқа созылды. Осы уақыт бойында қайық ағыс бойымен еркін
ақты. Мотор жөнделгеннен кейін қайық қайта бұрылып, салды алғашқы
кездескен жерден 7,5 км ара қашықтықта қуып жетті. Өзен ағысының
жылдамдығын тұрақты деп санап, ағыс жылдамдығын табу керек. ( 3
кмсағ).

Бірқалыпты-айнымалы қозғалыс
Бірқалыпты айнымалы қозғалыс дегеніміз кез келген тең уақыт аралығында
жылдамдық тең шамаларға өзгеретін қозғалыс. Бірқалыпты айнымалы қозғалыс
дегеніміз кез келген тең уақыт аралығында жылдамдық бірдей тең шамаларға
өзгереді.
Бірқалыпты айнымалы қозғалыс жылдамдығы артатын бірқалыпты үдемелі және
жылдамдығы кемитін бірқалыпты кемімелі қозғалыстарға бөлінеді.
Айнымалы қозғалыстың үдеуі, 1 секундта жылдамдықтың өзгерісімен
өлшенетін шама болып табылады
→
Танымал физикада Роджерс істің мәнін түсіндіру үшін кесте түсінігін
ұсынады:
а үдеу деген 1 секундта жылдамдықтың а мс артуы.
Сондықтан 2 - - -
а×2 мс
3 - -
- а ×3 мс
t - -
- a×t мс
Айнымалы қозғалыстың үдеуі деген уақыт бірлігінде жылдамдық
өзгерісімен өлшенетін шама.
Бірқалыпты-айнымалы қозғалысты Excel электронды кестелер көмегімен
зерттеуге болады:
a t S1= at2 2 S2 = (t+1)2 dS=S2-S1 k =dS(a2)
2
3 1 1,5 6 4,5 3
2 6 13,5 7,5 5
3 13,5 24 10,5 7
4 24 37,5 13,5 9
5 37,5 54 16,5 11
6 54 73,5 19,5 13
7 73,5 96 22,5 15
8 96 121,5 25,5 17
9 121,5 150 28,5 19
10 150 181,5 31,5 21
11 181,5 216 34,5 23
12 216 253,5 37,5 25
13 253,5 294 40,5 27
14 294 337,5 43,5 29

Үдеудің әр-түрлі мәндерін бере, біз бірдей уақыт аралығында жүріп өткен
жолдар жай сандарға жататынына көз жеткіземіз.
Қорытынды: бастапқы жылдамдықсыз бірқалыпты айнымалы қозғалыста
1. Жылдамдық уақытқа тура пропорционал.
2. Алғашқы секундта жүріп өткен жол, үдеудің жартысына тең.
3. Жол уақыттың квадратына тура пропорционал.
4. Бірдей уақыт аралығындағы жүріп өткен жолдар тізбегі тақ сандар
тізбегіне жатады.
Өз бетімен шығаруға арналған есептер
1. 20 мс бастапқы жылдамдықпен дене, 6 мс2 үдеу алады және бірталай
уақыттан кейін 80 мс жылдамдыққа ие болады. Уақытты және сол уақыттағы
жүрілген жолды табу керек.
2. Дене қандай үдеу алады және қанша жол жүреді, егер ол 3 мс
жылдамдықпен қозғала бастап, 6 секундтан кейін 45 мс жылдамдыққа ие
боласа?
3. екенін дәлелдеу қажет.
4. Барлық уақытта өткен жол арқылы V0=0 болған жағдайдағы соңғы
жылдамдықты қалай өрнектеуге болады?
5. Дене 40 мс жылдамдықпен вертикаль жоғары лақтырылған. 2 және 5 с
кейін дененің жылдамдығы қандай болады? Қандай жол жүреді және осы уақыт
аралығында орын ауыстыруы қандай болады?
Компьютерді сабақта қолдануға келесі мақалалар көмектеседі:
Богуславский А.А., Щеглова И.Ю. Моделирование физических задач в
электронных таблицах MS Excel. Журнал Информатика и образование, № 7 –
2004
Плеухова Л.Ф., Ситников Ю.К. Решение задач по физике средствами MS
Excel. Журнал Информатика и образование, № 4 – 2003.

Терең, берік білім тек қана жақсы мазмұндау мен көрнекіліктерді
қолданудан ғана жеткілікті емес, сондай-ақ оқу үрдісіндегі оқушылардың
үнемі белсенді қатысуына да байланысты болады.
Дүниеде ең керемет ашулардан да маңызды нәрселер бар – ол сол ашуларды
жасаған әдістерді білу - Г. Лейбниц.

Айнымалы қозғалыс
Айнымалы қозғалыс кезінде бірдей уақыт аралықтарында дененің жүрген
жолдары бірдей болмайды.
Айнымалы қозғалыстың лездік жылдамдығы деген жылдамдық анықталып
отырған уақыт аралығы шексіз кемігенде, орташа жылдамдық ұмтылатын шек
болып табылады.
Айнымалы қозғалыстың орташа жылдамдығы дегеніміз дене бірдей уақыт
аралығында бірдей жол жүретін бірқалыпты жылдамдық.
Есеп. А қаласынан В қаласына автобус V1 жылдамдықпен келді, ал кері
қайтқандағы жылдамдығы V2 . Қозғалыстың орташа жылдамдығын табу керек.
Қалалардың арасындағы ара қашықтық S болсын. Онда , ал
және .
Демек,
.
Заңдылықтарды график түрінде де қарастыруға болады:

Орта сызығы екінші және үшінші жағдайда тең үлкен фигураларды қосады
және жояды, яғни егер дене t с V1 жылдамдықпен, сондай уақытта V2
жылдамдықпен қозғалса, онда орташа жылдамдықты орташа арифметикалық
жылдамдық ретінде анықтауға болады. Бірқалыпты үдемелі қозғалыс кезінде
орташа жылдамдық бастапқы және соңғы жылдамдықтардың қосындысының жартысына
тең болады.

Өз бетімен шығаруға арналған есептер
1. Автомобиль жарты жолды 60 кмсағ жылдамдықпен жүріп өтті, қалған
жолдың жарты уақытын 15 кмсағ жылдамдықпен, соңғы бөлікті 45 кмсағ
жылдамдықпен жүреді. Барлық жолдағы автомобильдің орташа жылдамдығын табу
керек.
2. Поезд бірінші жарты жолды екінші жарты жолға қарағанда 1,5 есе үлкен
жылдамдықпен жүреді. Барлық жолдағы поездың орташа жылдамдығы 43,2 кмсағ.
Бірінші және екінші жарты жолдағы поездың жылдамдықтары қандай?
3. Өзен және бойымен ары-бері жолына бірдей уақыт кете ме? Жүрілген ара
қашықтық бірдей.
Орташа және орташа арифметикалық жылдамдықтардың мәндерін Excel
көмегімен көруге болады:
V1 V2 Vорташа Vорт.арифметикалық
12 15 13,33333333 13,5
12 25 16,21621622 18,5
12 36 18 24
12 120 21,81818182 66

Орташа және орташа арифметикалық жылдамдықтардың айырмашылықтары келесі
графиктерден жақсы көрінеді:

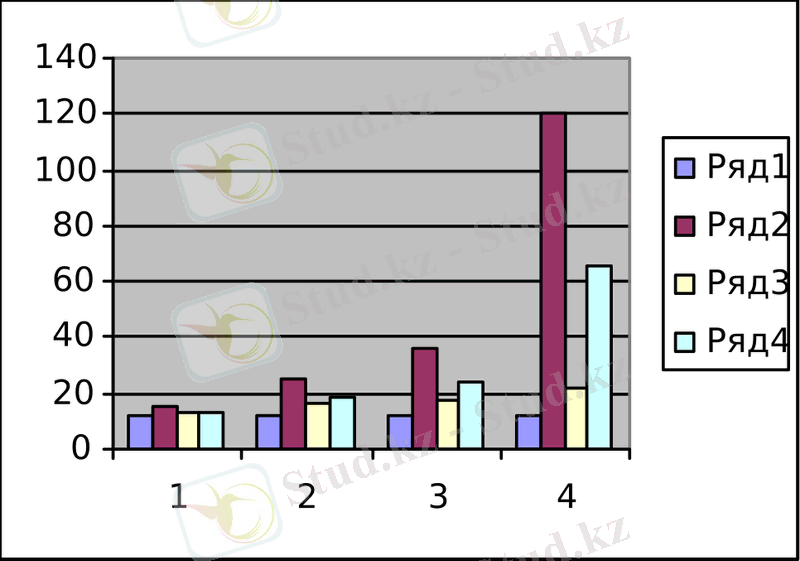
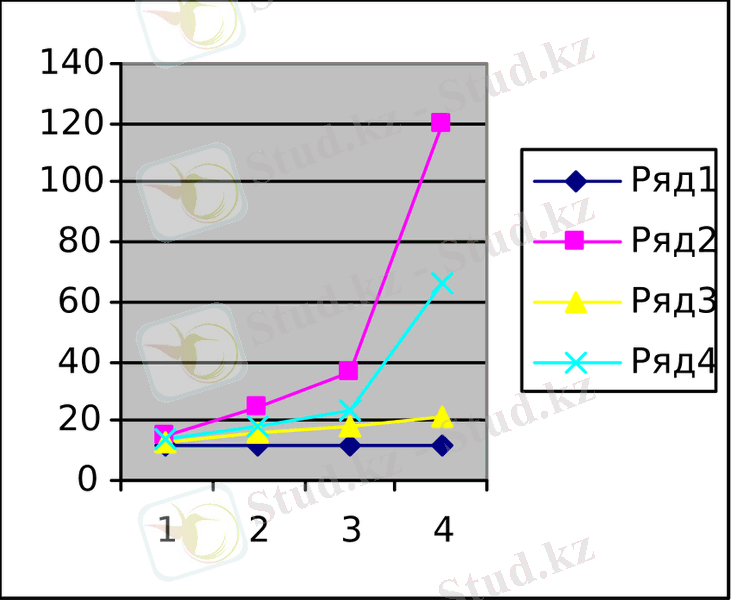
Қозғалыстың тәуелсіздік принциптері

Егер дене бір уақытта бірнеше қозғалыстарға өатыса алады, олардың
әрқайсысы бір-біріне бағынбайды.

Мысал. Горизонтқа бұрышпен, V жылдамдықпен лақтырылған дененің
ұшу ұзақтығын табу керек.

Дене екі қозғалысқа қатысады:
- горизонтпен (Vt векторы) α бұрыш
жасайтын, түзу бойындағы бірқалыпты
қозғалыс;

- еркін түсу ( gt22 векторы).
Осы векторлардың қосындысы түсу нүктесін береді.
Барлық шамалар тікбұрышты үшбұрыштан оңай анықталады.

Өз бетімен шешуге арналған есептер
1. Ені d=2,4 м, v1=15мс жылдамдықпен қозғалатын вагон вагонның
қозғалысына перпендикуляр ұшқан оқпен атқыланады. Вагонның қабырғаларындағы
тесіктердің ығысуы бір-бірімен салыстырғанда 1=6 см тең. Оқ қозғалысының
жылдамдығы қандай? (600 мс).
1. Тегіс үстелде тез айналатын конус формасындағы зырылдауық қозғалып
тұр. Қандай ең аз жылдамдықта зырылдауық үстелдің қырына соғылмайды.
Конустың биіктігі һ, радиусы r. (, V≥ ).
2. Егер жеңіл автомобильдің жүргізушісі алға қарай горизонтқа 600
бұрышқа көлбей жатқан артқы әйнекке жаңбыр тамшысы ізін қалдырмағанын
байқаса және автомобильдің жылдамдығы 30 кмсағ көп болса, түскен
жаңбыр тамшысының жылдамдығы қандай? (14,4 мс).
3. Екі вертикаль жазықтық арасында орналасқан нүктеден горизонтқа α
бұрыш жасай доп лақтырылады. Егер доп екі жазықтықтан да серпімді
шағылып лақтыру нүктесіне түссе, ұшудың бастапқы жылдамдығы қандай?
Жазықтықтар арасындағы ара қашықтық L. ().

Есептерді шығарудың координаттық әдісі
Көмпьютерге берілген бағдарлама бойынша берілген теңдеуді немесе
теңдеулер жүйесін есептеу үшін тек қана қажет шаманы еңгізу жеткілікті
болғандықтан, қозғалыс теңдеулері көмегімен есептер шығаруда көмпьютерді
қолдану өте ыңғайлы. Жалпы жағдайда теңдеуге векторлық шамалар кіреді,
сондай-ақ олардың координата осіндегі проекциялары оң және теріс болуы
мүмкін.
Мысал:
А нүктесінен 45 м биіктіктен дене еркін түседі. Бір уақытта А
нүктесінен 21 м төмен жатқан В нүктесінен вертикаль жоғары екінші дене
лақтырылады. Егер екі дене де жерге бір уақытта түссе, екінші дененің
лақтыру жылдамдығын табу керек.

Бірінші дененің түсу шартынан түсу уақыты табылады
.
Екінші дене , биіктікке көтеріле, жоғары
қозғалып барады және одан кейін биіктіктен құлайды,
жауабын табу үшін неғұрлым күрделі теңдеулерді
шешу қажет болады:
= .
2. Қозғалыс теңдеулерін қолдану арқылы есепті шығарайық: Х осі жоғары
бағытталсын және координата басы жерде болсын. Онда дене қозғалыстарының
теңдеулері былай болады

.
Екі дене де t секундтан кейін жерде, яғни координатасы нөлге тең
болатын О нүктесінде болады, екі теңдеу аламыз:

.
Біріншіден t табамыз, бірінші және екінші теңдеулерді салыстра, аламыз
,
мұнда бір ғана белгісіздік болады.
3. Егер қозғалыстардың тәуелсіздік принциптерін қолдансақ, векторларды
қосу арқылы жауабын ала аламыз:
А бірінші дененің орын ауыстыруы векторымен анықталады.
В екінші ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.