Сандық әдістер пәні: Ақпараттық жүйелер мамандығы студенттеріне арналған әдістемелік нұсқау


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:
Әдістемелік нұсқаудың
титулдық парағы

Нысан
ПМУ ҰС Н 7. 18. 3/40
Қазақстан Республикасы білім және ғылым министірлігі
С. Торайғыров атындағы Павлодар мемлекеттік университеті
Информатика және ақпараттық жүйелер кафедрасы
5В070300 - Ақпараттық жүйелер мамандығы студенттеріне
Сандық әдістер пәнінен
пәнді оқып-үйренуге арналған әдістемелік нұсқау
Павлодар
Әдістемелік нұсқауды
бекіту парағы

Нысан
ПМУ ҰС Н 7. 18. 3/41
БЕКІТЕМІН
ОІ жөніндегі проректор
Пфейфер Н. Э.
(қолы)
«___»2010 ж.
Құрастырған: аға оқытушы Ардабаева Алмагуль Кайрбаевна
Информатика және ақпараттық жүйелер кафедрасы
5В070300 - Ақпараттық жүйелер мамандығы студенттеріне
Сандық әдістер пәнінен
пәнді оқып-үйренуге арналған әдістемелік нұсқау
Кафедра отырысында ұсынылған 2010 ж. «___» №хаттама
Кафедра меңгерушісі Асаинова А. Ж.
(қолы)
Физика, математика және ақпараттық жүйелер факультеттің әдістемелік кеңесімен құпталған 2010 ж. «» №хаттама
ӘК төрағасы Мұқанова Ж. Ғ. «»2010 ж.
(қолы) (күні)
КЕЛІСІЛДІ
Факультет деканы Нұрбекова Ж. К. «» 2010 ж.
(қолы) (күні)
Жжәқб құпталды
ЖжӘҚБ бастығы Варакута А. А. « » 2010 ж.
(қолы) (күні)
Университеттің әдістемелік кеңесімен құпталған
«» 2010 ж. №хаттама
- тақырып. Кіріспе
Сандық әдістер. Есептеу эксперимент және математикалық моделдер туралы түсінік. Сандық әдістеріне қойылатын талаптар.
Ғылыми зерттеулерде аумақты есептеу жұмыстары үшін есептеуіш техниканы пайдалану аса табысты нәтижелерге жеткізуде. Шынында, қазіргі төртінші буынның ЭЕМ-нің бір секундта орындайтын операия саны милиардтап есептелінеді. Демек, ол адамның бірнеше күнде орындайтын есепту жұмыстарын бірнеше сағатта ғана орындай алады. Бірақ, ЭЕМ тек қана адамның ой еңбегімен құрылған программа бойынша берілген тапсырманы ғана орындай алады. Ол үшін біздер ақиқат дүниедегі әр түрлі құбылыстардың математика тілінде моделін білуіміз қажет. Қолданбалы есептер табиғаттағы құбылыстар, физикалық, химиялық, жоспарлауда басқару жүйелері және тағы да басқа нақтылы объектілермен байланысты. Мұндай есептерді тұжырымдау үшін көбінесе әуелі зерттеленетін объектінің ең маңызды қасиеттері мен ерекшеліктерін, қажетті параметрлерін анықтайды. әрі қарай оларды математикалық қатыстар, белгілер арқылы сипаттайды. Осы процесті математикалық құру деп атайды. Сонымен, математикалық модельдеу - табиғаттағы кейбір құбылыстар кластарын математикалық белгілер, формулалар көмегімен өрнектеу арқылы жуықтап жазу.
Математикалық моделдеуге қойылатын талаптар :
- математикалық моделдеудің қарастыратын құбылысқа барабарлығы (адекваттылығы), дәлірек айтқанда мдель құбылыстың негізгі ерекшеліктерін, қасиеттерін жеткілікті, дәл және айқын сипаттау қажет;
- математикалық моделдеу қарапайым, зертеуге түсінікті және ыңғайлы (доступный) болуы қажет.
Қолданбалы математикада мұндай талаптарды қанағаттандыратын құбылыстың математикалық мөделін құру оңай емес, ол ғылыми техникалық есепті шешу барысында аса күрделі және қиын кезеңінің бірі.
Ұсынылатын әдебиеттер: [1], [2], [3]
2-тақырып. Сызықты теңдеулер жүйелерінің шешудің итерациялық әдістері
Негізгі ұғымдар. Сызықтық жүйелер. Сызықты теңдеулер жүйелердің шешім әдістері туралы Тура әдістер. Басты элементер әдісі (Гаусс әдісі) . Квадраттық түбірлер әдісі. Халецкий әдісі.
Математикалық моделдеудің кмегімен ғылыми-техникалық қолданбалы есептерді шығару таза математикалық есептерді шығаруға болады. Ал, математикалық есепті шығару үшін негізінен келесі үш әдіс олданылады: графикалық, аналитикалық, сандық әдістер.
- г рафикалық әдіс. Бұл әдіспен кейбір жағдайда ізделінетін шаманың ретін анықтауға болады. Мұның негізі - есептің шешуін функцияның графигін салу көмегімен табу.
- аналитикалық әдіс. Мұнда есептің шешімін формула көмегімен өрнектеуге болады. Мысалы: қарапайым алгебралық, тригонометриялық, трансценденттік, дифференциалдық теңдеудің шешімі.
- сандық әдістер. Қазіргі кезде күрделі математикалық есептерді шығарудың негізгі құралы сандық әдістер. Сандық әдістер есептің шешімін сандарға қолданылатын саны шектеулі арифметикалық операциялар орындауға келтіріледі және нәтижесін андық мәндер арқылы береді.
Теңдеуді шешу - оның түбірлері болатынын, егер бар болатын болса нешеу екенін және оларды белгілі дәлдікпен мәндерін анықтау.
түріндегі сызықтық емес теңдеулердің түбірлерін табу есебі әртүрлі ғылыми зерттеулерде кездеседі (мұндағы
Әрбір
Сызықтық емес теңдеулерді шешудің әдістері тура және итерациялық болып бөлінеді. Тура әдістер түбірлерді шекті қатынас (формула) түрінде жазуға мүмкіндік береді. Мектеп курсынан тригонометриялық, логарифмдік, көрсеткіштік, сонымен қатар қарапайым алгебралық теңдеулерді шешу үшін әдістер белгілі. Бірақ та тәжірибеде теңдеулердің мұндай әдістермен шешілмейтіндері де кездеседі. Оларды шешу үшін итерациялық әдістер пайдаланады, яғни тізбектелген жуықтау әдістері (сандық әдістер) .
Теңдеудің түбірлерін сандық әдіспен табу есебі екі кезеңнен тұрады: түбірлерді айыру, яғни түбірдің бір ғана мәнін қамтитын жеткілікті аз (сығылған) аймақтарды табу және түбірлерді анықтау, яғни қандайда бір аймақтағы түбірді белгілі дәлдікпен есептеу.
Ұсынылатын әдебиеттер: [1], [2], [3]
3-тақырып. Сызықты теңдеулер жүйелерін шешудің дәл әдістері
Итерация әдісі. Итерациялық процесстің жинақталуының жеткілікті шарты. Итерациялық процесстің жинақталуының қажетті және жеткілікті шарты. Сызықты теңдеулер жүйесін шешудің итерациялық әдістерінің жалпы схемасы. Релаксациялық принципі. Зейдель әдісі. Минимальді үйлесімсізділік әдісі және оның қателігі. Жылдам түсу әдісі. Жылдам түсу әдісі жинақталу жылдамдығының бағасы. Матрицаның меншікті мәндері мен векторларын табу. Меншікті мәндер мәселесі. Матрициның модулі бойынша ең үлкен меншікті мәнін және соған сәйкес меншікті векторын итерация әдісімен есептеу.
Итерациялық әдістер - біртіндеп жуықтау әдістері. Мұнда жуықталған шешімін беру керек - бастапқы жуықтау. Бұдан кейін алгоритм көмегімен есептеудің бір циклі жүргізіледі (итерация деп аталады) . Итерация нәтижесінде жаңа жуықтау алынады. Итерация талап етілетін дәлдікпен шешім алынғанға дейін жүргізіледі. Итерациялық әдістерді пайдаланып сызықтық теңдеулерді шешудің алгоритмдері тура әдістермен салыстырғанда өте күрделі.
Алгебралық және трансценденттік теңдеулерді итерация әдісімен шешу. Сығып бейнелеу принципі және оны теңдеулер шешудің итерациялық әдістерінің жинақтылығын зерттеуге қолдану. Қиюшылар әдісі. Ньютон әдісі, Ньютон-Канторович әдісі. Аралас әдісі. Осы әдістердің жинақтылығы.
Айталық бізге
түріндегі теңдеу берілсін. Мұндағы
теңдеуімен алмастыруға болады. Мұндай жағдайда
Мысал 1.
Түбірлерін графикалық түрде айыру үшін, оны оған мәндес
Графикке қарап, оның
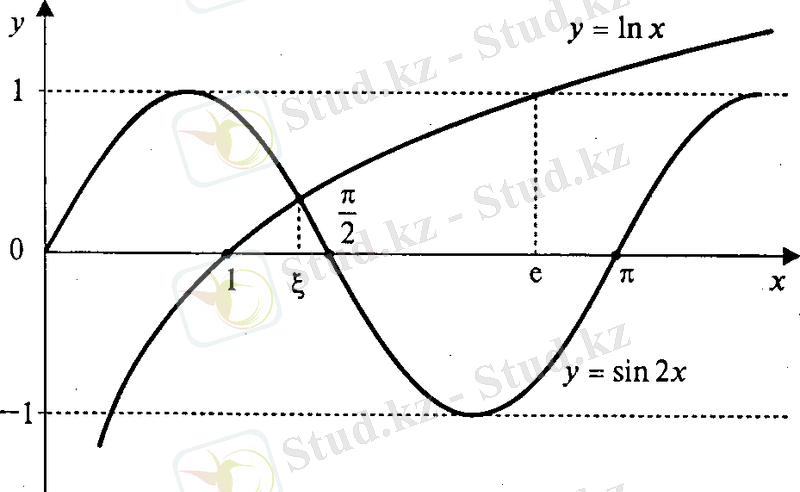
Түбірлерді айыру туралы есептерді шешу барысында келесі жайттардың пайдасы бар:
- Егеркесіндісінде үздіксізфункциясы, оның шеткі нүктелерінде әртүрлі таңбалы мәндер қабылдаса (яғни) , онда берілген теңдеудің осы кесіндіде кем дегенде бір түбірі бар болады.
- Егерфункциясы монотонды (кемімелі немесе өспелі) болса, кесіндісіндегі түбір жалғыз ғана болады.
Тексеру үшін
Қарапайым жағдайда, түбірлерді графикалық айыруды қолмен еептеуге болады, кейде күрделі жағдайларда теңдеудің түбірі берілген кесіндіде болуын (санын) анықтауда компьютердің қолданбалы бағдарламасын пайдалануға немесе программалау тілінде программа құрастыруға болады.
Айталық
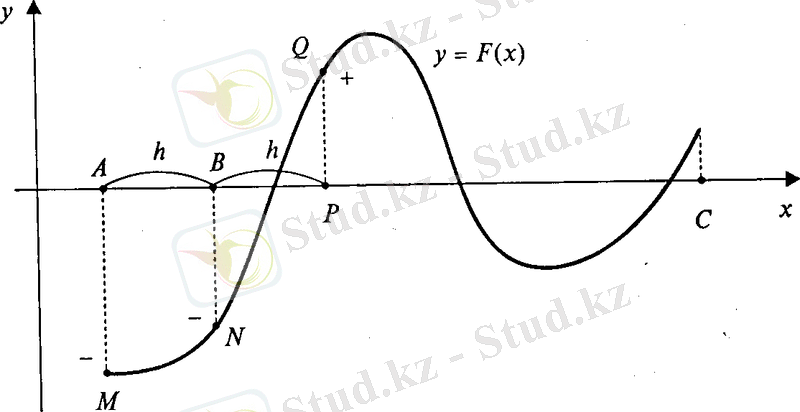
Теңдеудің шешімін программалау тілі көмегімен қарастырайық. Осыған сәйкес келетін алгоритмнің жалпы схемасын көрсетейік. Қойылған есептің нәтижесі экранда көрсетілген
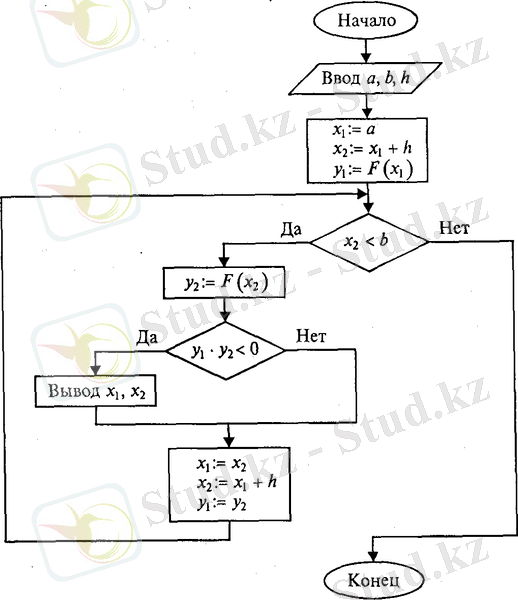
Ұсынылатын әдебиеттер: [3], [4], [5]
4-тақырып. Функцияларды жуықтау
Интерполяция есебіеің қойылуы. Интерполяция және қалпына келтіру. Арифметикалық амалдар саны туралы түсінік. Интерполяциялық формулалары қателілігінің бағасы және оларды минимизациялау. Нормаланған кеңістііктегі ең жақсы жуықтау. Ақырлы айырымдар. Ньютонның бірінші және екінші интерполяциялық формулалары. . Орта айырымдар кестесі. Гаусс, Стирлинг, Бессель интерполяциялық формулалары. Тұрақты қадамды интерполяциялық формулаларының жалпы сипаттамасы. Лагранж интерполяциялық формуласы. Ең жақсы интерполяциялық түйіндерін таңдап алу.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz