Гиперболалық түрдегі операторлардың бір класының симметриялылығын зерттеу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 41 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . 3
I-бөлім. Функционалдық анализдің негізгі түсініктері мен кейбір фактілері. . . .
1. 1. Метрикалық кеңістік түсінігі. Гельдер және Минковский теңсіздіктері . . .
1. 2. Сызықты және нормаланған кеңістіктер . . .
1. 3. Гильберт кеңістігі . . .
1. 4. Сызықты операторлар теориясының элементтері . . .
1. 5. Кері операторлар . . .
1. 6.
 кеңістігі . . .
кеңістігі . . .
1. 7.
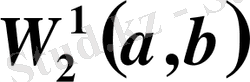 кеңістігі . . .
кеңістігі . . .
1. 8. Түйіндес операторлар . . .
1. 9 Тұйық операторлар . . .
II. бөлім. Тербелістер теңдеуі. . . .
2. 1. Ішектің тербелісінің теңдеуін қорытып шығару. Шексіз ішек.
Даламбер формуласы. Фурье әдісі . . .
2. 2. Еріксіз электр тербелістерінің дифференциал теңдеуі.
(Телеграф теңдеуі. ) . . .
2. 3. Мембрана тербелісінің теңдеуін қорыту. (Тік бұрышты мембрана тербелістері Дөңгелек мембрана тербелісі. ) . . .
III. бөлім. Гиперболалық түрдегі оператордың бір
класының симметриялылығы. . . .
3. 1. Симметриялы операторлар . . .
3. 2.
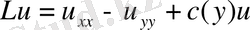 түрдегі гиперболалық оператордың бір
түрдегі гиперболалық оператордың бір
класының симметриялылығы туралы . . .
Қорытынды. . . .
Әдебиеттер . . .
Кіріспе
Тербелмелі қозғалыстармен байланысты физикалық есептерде екінші реттік гиперболалық теңдеулер типі кездеседі. Гиперболалық теңдеудің жай түрі:
U xx -U yy =0 (1)
кейде оны ішектің тербеліс теңдеуі деп атайды.
Жұмыстың мақсаты. Гиперболалық түрдегі оператордың бір класының симметриялы болатындығы туралы мәселені зерттеу болып табылады.
Зерттеу әдістемесі. Сызықты екінші ретті екі мүшелі дифференциалды операторды зерттеу барысында төмендегідей әдістер пайдаланылды: локализация әдісі, априорлы бағалау әдісі және М. Б. Мұратбеков пен М. Өтелбаевтың жұмыстарында ұсынылған әдістер қолданылды.
Ғылыми жаңашылдығы. Жұмыста төмендегідей жаңа нәтижелер алынды:
- сызықты екінші ретті дифференциалды оператордың өз-өзіне түйіндес болатындығы көрсетілді.
Ғылыми жұмыстың құрылымы. Ғылыми жұмыс кіріспеден, үш тараудан, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады. Теоремалардың, формулалардың нөмірленуі екі таңбалы: бірінші сан тараудың нөмірін, ал екіншісі теоремалардың жеке нөмірін білдіреді. Ғылыми жұмыс . . . беттен тұрады.
Ғылыми жұмыстың негізгі мазмұны.
Кіріспе де тақырыптың өзектілігі негізделген, негізгі мақсаттары келтірілген, жұмыстың жаңалығы мен теориялық және практикалық маңыздылығы анықталған.
Бірінші тарауда қажетті белгілеулер, анықтамалар және көмекші нәтижелер келтірілген.
Екінші тарауда: Гиперболалық түрдегі теңдеулер зерттелген, яғни ішектің тербеліс теңдеуі, Даламбер формуласы, айнымалыны ажырату немесе Фурье әдістері көрсетілген.
Үшінші тарауда гиперболалық түрдегі оператордың бір класының симметриялылығы зерттелінген.
I-бөлім. Функционалдық анализдің негізгі түсініктері мен кейбір фактілері
1. 1. Метрикалық кеңістік, анықтамасы, мысалдар
1. Метрикалық кеңістік анықтамасы.
 - қайсыбір бос емес жиын болсын.
- қайсыбір бос емес жиын болсын.
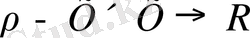 , мұндағы
, мұндағы
 -
-
 және
және
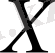 жиындарының декарт
жиындарының декарт
көбейтіндісі, ал
 - нақты сандар жиыны
- нақты сандар жиыны
Анықтама:
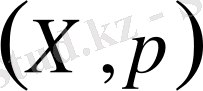 жұбы метрикалық кеңістік деп аталады.
жұбы метрикалық кеңістік деп аталады.
Егер
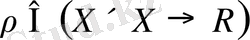 бейнелеуі мынадай шарттарды қанағаттандырсын
бейнелеуі мынадай шарттарды қанағаттандырсын
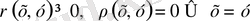
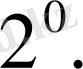
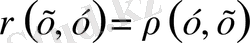 (1)
(1)
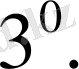
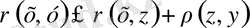
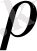 осы шарттарды қанағаттандырса
осы шарттарды қанағаттандырса
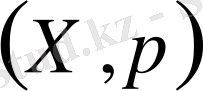 жұбы метрикалық кеңістік деп аталады.
жұбы метрикалық кеңістік деп аталады.
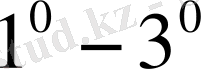 шарттар метрикалық кеңістіктің аксиомалары деп аталады.
шарттар метрикалық кеңістіктің аксиомалары деп аталады.
 - тепе-теңдік, 2-симметрия, 3- үшбұрыштың аксиомалары деп аталады.
- тепе-теңдік, 2-симметрия, 3- үшбұрыштың аксиомалары деп аталады.
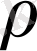 - бейнелеуі
- бейнелеуі
 жиынында анықталған арақашықтық немесе метрика деп аталады.
жиынында анықталған арақашықтық немесе метрика деп аталады.
Енді бірнеше метрикалық кеңістікке мысалдар келтіреміз. Бұл мысалдарда келтірілген кейбір метрикалық кеңістіктер функционалдық талдаудың өте маңызды рөль атқарады.
- Оқшауланған нүктелер метрикалық кеңістігі
 - қайсыбір бос емес жиын болсын және
- қайсыбір бос емес жиын болсын және
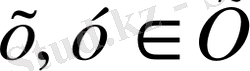 болсын.
болсын.
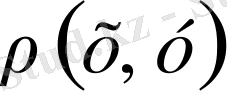 метрикасын мына төменде келтірілген формула бойынша анықтаймыз
метрикасын мына төменде келтірілген формула бойынша анықтаймыз
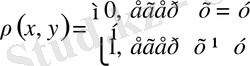 (2)
(2)
1) және 2) аксиомалардың орындалуы оңай көрініп тұр. Сондықтан біз 3)
 - үшбұрыш аксиомасының орындалуын тексереміз.
- үшбұрыш аксиомасының орындалуын тексереміз.
Егер
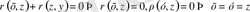 сондықтан
сондықтан
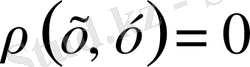 .
.
Демек, бұл жағдайда
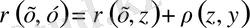
Ал егер (
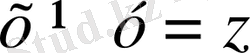 немесе
немесе
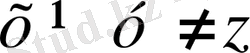 немесе
немесе
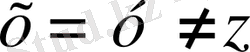 ) болса
) болса
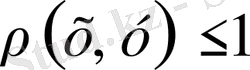 және
және
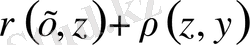 .
.
Сондықтан
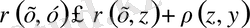
Сонымен
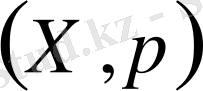 - метрикалық кеңістік, ол оқшауланған нүктелердің метрикалық кеңістігі деп аталады.
- метрикалық кеңістік, ол оқшауланған нүктелердің метрикалық кеңістігі деп аталады.
- Нақты сандар метрикалық кеңістігі
R нақты сандар жиынында
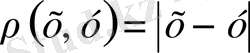 метрикасын енгіземіз. Осының нәтижесінде
метрикасын енгіземіз. Осының нәтижесінде
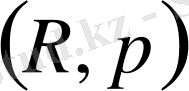 - метрикалық кеңістікке айналады. Метрикалық кеңістіктің аксиомалары өте жеңіл орындалады. Сондықтан біз оларды келтіреміз.
- метрикалық кеңістікке айналады. Метрикалық кеңістіктің аксиомалары өте жеңіл орындалады. Сондықтан біз оларды келтіреміз.
Гельдер және Минковский теңсіздіктері
Функционалдық талдауда кездесетін негізгі кеңістіктерді зерттеу үшін біз өте қажет мәселелер ретінде Гельдер және Минковский теңсіздіктерін келтіреміз. Бұл теңсіздіктердің функционалдық талдау үшін өте маңызы зор.
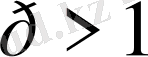 болсын.
болсын.
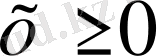 үшін
үшін
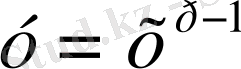 функциясын қарастырамыз. Бұл функция биективтік функция (өзара бірмәнді) . Бұл функцияның кері функциясы бар, ол
функциясын қарастырамыз. Бұл функция биективтік функция (өзара бірмәнді) . Бұл функцияның кері функциясы бар, ол
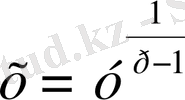 болады.
болады.
 санын алайық та
санын алайық та
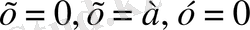 және
және
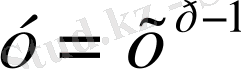 сызықтарымен шектелген қисық сызық трапецияны қарастырайық. Оның ауданы
сызықтарымен шектелген қисық сызық трапецияны қарастырайық. Оның ауданы
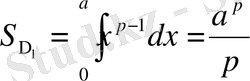
болады.
Дәл осы жолмен
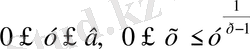 сызықтарымен шектелген
сызықтарымен шектелген
 қисық сызықты трапециясының ауданын табайық
қисық сызықты трапециясының ауданын табайық
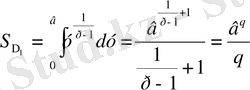
Мұндағы
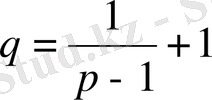 . Соңғы теңдікті пайдаланып мынадай теңдік табамыз.
. Соңғы теңдікті пайдаланып мынадай теңдік табамыз.
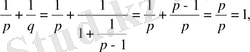
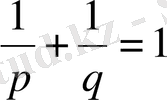 (3)
(3)
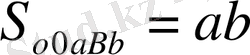 . Сондықтан
. Сондықтан
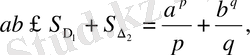
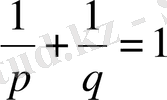 (4)
(4)
Теріс емес а және в сандары үшін өте маңызды теңсіздік таптық.
Енді
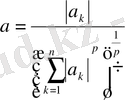 ,
,
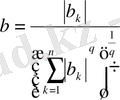
(4)

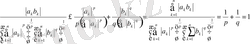

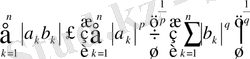 -
-
бұл Гельдер теңсіздігі деп аталады.
Миньковский теңсіздігі
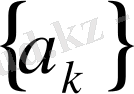 және
және
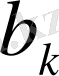 теріс емес сандар болсын, осы жағдайда мынадай теңсіздік орындалады.
теріс емес сандар болсын, осы жағдайда мынадай теңсіздік орындалады.
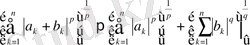
Дәлелдеу.
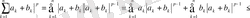
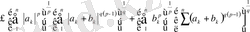 .
.
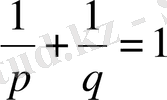

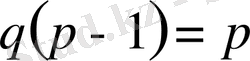 .
.
Соңғы теңсіздіктің екі жағын да
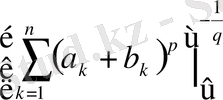
көбейтіп, мынадай теңсіздікке келеміз
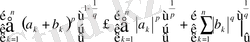 ,
,
бұл біздің іздеген теңсіздігіміз.
2. Гельдер және Миньковскийдің интегралдық теңсіздіктері
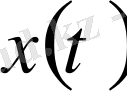 және
және
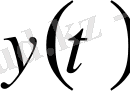 функциялары
функциялары
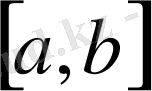 кесіндісінде үздіксіз болсын.
кесіндісінде үздіксіз болсын.
Мынадай теңсіздіктер орындалады
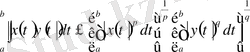
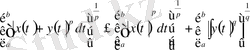 .
.
Бұл теңсіздіктерді дәлелдеусіз атап өтеміз.
Метрикалық кеңістіктерге мысалдар
1)
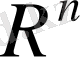 кеңістігінде кез келген әртүрлі реттелген
кеңістігінде кез келген әртүрлі реттелген
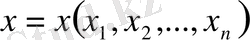 және
және
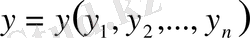 нүктелері үшін метриканы мына түрде аламыз.
нүктелері үшін метриканы мына түрде аламыз.
.
мұндағы:
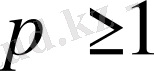
1) және 2) аксиомалардың орындалатыны жеңіл көрініп тұр. 3) аксиоманың орындалатынын тексерейік
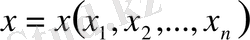 ,
,
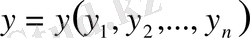 және
және
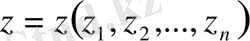 болсын.
болсын.
Дәлірек айтқанда біз мынадай теңсіздікті дәлелдеуіміз керек
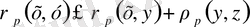 (2)
(2)
Егер
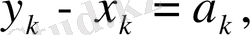
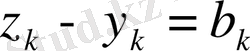 деп белгілесек
деп белгілесек
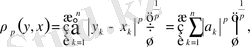
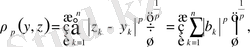
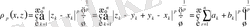
Енді (2) теңсіздік пен соңғы келтірілген теңсіздіктерді пайдаланып жазсақ мынадай түрге енеді.
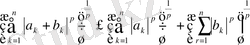 -
-
бұл Миньковский теңсіздігі ,
олай болса (2) теңсіздігі орындалады. Бұл метрикалық кеңістікті
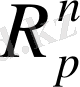 -
деп белгілейміз.
-
деп белгілейміз.
2)
 болғанда бұл кеңістік n-өлшемді арифметикалық
болғанда бұл кеңістік n-өлшемді арифметикалық
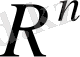 евклид кеңістігіне айналады.
евклид кеңістігіне айналады.
3) Барлық нақты сандардың шектелген тізбегін жиынын қарастырайық:
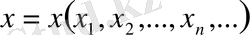 ,
,
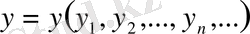 осы жиынның кез келген екі элементі болсын
осы жиынның кез келген екі элементі болсын
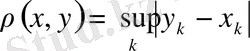
бұл метрика 1) - 3) аксиомаларды қанағаттандырады. Сондықтан аталған жиын метрикалық кеңістік болады, оны
 деп белгілейміз.
деп белгілейміз.
4)
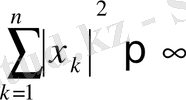 теңсіздігін қанағаттандыратын шексіз
теңсіздігін қанағаттандыратын шексіз
 сан тізбектерінің жиынын қарастырайық. Оны
сан тізбектерінің жиынын қарастырайық. Оны
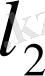 деп белгілейміз.
деп белгілейміз.
Осы жиында кез келген екі элементтің арақашықтығы
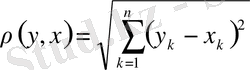
теңдігі арқылы анықтасақ ол метрикалық кеңістікке айналады. Ол үшін мынадай элементар теңсіздікті пайдаланамыз.
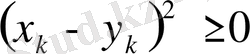
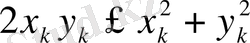

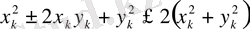
немесе
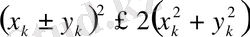
Соңғы теңсіздіктен
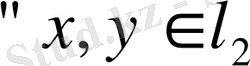 үшін
үшін
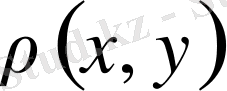 шамасының мағынасы бар болады, немесе
шамасының мағынасы бар болады, немесе
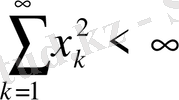 және
және
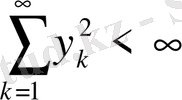

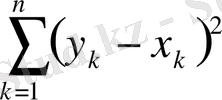
1) және 2) аксиомалардың орындалуы жеңіл дәлелденеді, ал 3) аксиома мына төмендегі теңсіздіктерден шығады (р=2 болғанда Миньковский теңсіздігі)
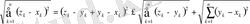
Бұл теңсіздікте
 шекке көшу арқылы мына теңсіздікті аламыз
шекке көшу арқылы мына теңсіздікті аламыз
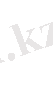
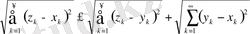
Бұл кеңістік
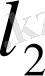 кеңістігі деп аталады.
кеңістігі деп аталады.
Дәл осы жолмен
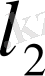 кеңістігін
кеңістігін
 -ге жалпылауға болады.
-ге жалпылауға болады.
2. Сызықты және нормаланған кеңістіктер.
Анықтама 2. 1.
 жиыны сызықты кеңістік деп аталады, егер
жиыны сызықты кеңістік деп аталады, егер
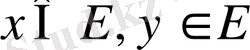 үшін осы элементтердің қосындысы деп аталатын, келесі шарттарды қанағаттандыратын
үшін осы элементтердің қосындысы деп аталатын, келесі шарттарды қанағаттандыратын
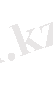
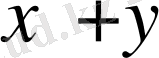 амалы анықталса:
амалы анықталса:
1. егер
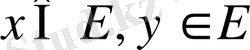 болса, онда
болса, онда
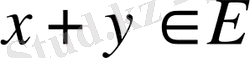
2.
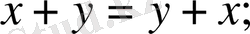 ;
;
3.
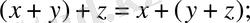
4. Барлық
 үшін
үшін
 болатын «нөлдік» элемент бар және
болатын «нөлдік» элемент бар және
 жиынында келесі шарттарды қанағаттандыратын
жиынында келесі шарттарды қанағаттандыратын
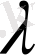 санына көбейту амалы анықталса:
санына көбейту амалы анықталса:
5. егер
болса, онда
болады(мұндағы
скаляр шама) ;
6.
-скалярлар;
7.

8. (сол жағында нөл саны, ал оң жағында
«нөлдік» элемент) ;
9.
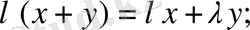
10.
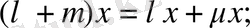
Мұнда
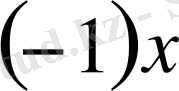 элементі
элементі
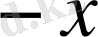 арқылы белгіленеді. Жоғарыдағы қасиеттерден
арқылы белгіленеді. Жоғарыдағы қасиеттерден
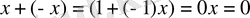 және
және
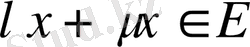 болатынын көреміз.
болатынын көреміз.
Кей жағдайда сызықты кеңістікті векторлық кеңістік деп, ал оның элементтерін векторлар деп атайды. Сызықтық кеңістікте
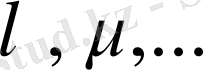 скаляр көбейткіштері нақты немесе комплекст болуына байланысты кеңістік те нақты немесе комплекс деп аталады.
скаляр көбейткіштері нақты немесе комплекст болуына байланысты кеңістік те нақты немесе комплекс деп аталады.
Мысалдар:
- Барлық нақты(комплекс) сандар жиыны нақты (комплекс) сызықтық кеңістік құрайды.
- Нақты(комплекс) коэффициентті бір айнымалы
көпмүшеліктер жиыны нақты(комплекс) сызықты кеңістік болады.
Анықтама 2. 2.
Сызықтық кеңістіктің
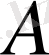 жиыны осы кеңістіктің ішкі кеңістігі деп аталады, егер
жиыны осы кеңістіктің ішкі кеңістігі деп аталады, егер
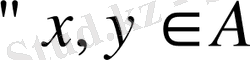 және
және
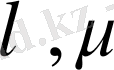 скалярлары үшін
скалярлары үшін
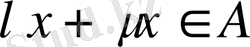 болса. Мұндай ішкі кеңістікті сызықты көпбейне деп атайды.
болса. Мұндай ішкі кеңістікті сызықты көпбейне деп атайды.
Кеңістіктің элементтерінің ұзындығы анықталған кеңістікті нормаланған кеңістік деп атайды.
Анықтама 2. 3.
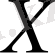 сызықты кеңістігінің әрбір
сызықты кеңістігінің әрбір
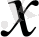 элементіне келесі шарттарды қанағаттандыратын
элементіне келесі шарттарды қанағаттандыратын
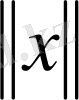 санын сәйкестендірсек:
санын сәйкестендірсек:
1.
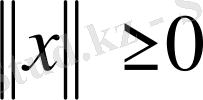 және
және
 ;
;
2.
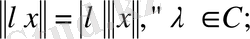
3.
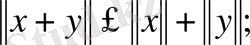
онда
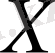 кеңістігі нормаланған кеңістік деп аталады.
кеңістігі нормаланған кеңістік деп аталады.
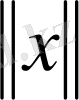 санын
санын
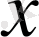 элементінің нормасы деп атаймыз. Егер
элементінің нормасы деп атаймыз. Егер
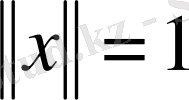 болса, онда
болса, онда
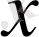 нормаланған элемент деп аталады. Мысалы, нақты(комплекс) сандар жиынында норма ретінде санның абсолют шамасын алсақ, онда ол нормаланған сызықты кеңістік болады. Сызықты нормаланған кеңістіктерде элементтердің арасындағы қашықтық ұғымын енгізуге болады. Нақты айтқанда келесі тұжырым орынды болады:
нормаланған элемент деп аталады. Мысалы, нақты(комплекс) сандар жиынында норма ретінде санның абсолют шамасын алсақ, онда ол нормаланған сызықты кеңістік болады. Сызықты нормаланған кеңістіктерде элементтердің арасындағы қашықтық ұғымын енгізуге болады. Нақты айтқанда келесі тұжырым орынды болады:
Лемма 2. 1.
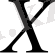 сызықты нормаланған кеңістігі
сызықты нормаланған кеңістігі
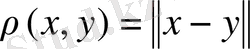 метрикасымен метрикалық кеңістік болады.
метрикасымен метрикалық кеңістік болады.
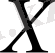 кеңістігінде осы метрика бойынша тізбектің жинақтылығы норма бойынша жинақтылықпен сай келеді.
кеңістігінде осы метрика бойынша тізбектің жинақтылығы норма бойынша жинақтылықпен сай келеді.
Лемма 2. 2. Сызықты нормаланған кеңістікте норма метрика мағынасында үзіліссіз функция болып табылады.
Анықтама 2. 4. Егер сызықты нормаланған кеңістік
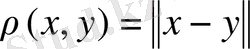
метрикасы бойынша толық метрикалық кеңістік болса онда сызықты нормаланған кеңістік толық деп аталады.
Толық сызықты нормаланған кеңістік банах кеңістігі деп аталады.
Теорема 2. 1. Әрбір сызықты нормаланған кеңістік қандайда бір банах кеңістігіне енеді және сол кеңістікте тығыз болады.
3. Гильберт кеңістігі.
Анализде функциялардың скаляр көбейтіндісі кеңінен қолданылады. Сондықтан скаляр көбейтінді енгізілген сызықты кеңістікті қарастырған жөн болады.
Анықтама 3. 1.
Айталық
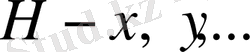 элементтерінің қандай да бір жиыны болсын.
элементтерінің қандай да бір жиыны болсын.
I. Егер
 жиынында
жиынында
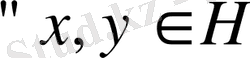 үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
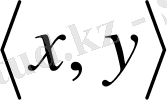 енгізілсе:
енгізілсе:
1.
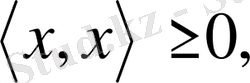 және
және
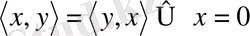
2.
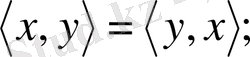
3.
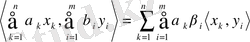 ;
;
II.
 жиынында
жиынында
 үшін n сызықты тәуелсіз векторлар табылса, яғни
үшін n сызықты тәуелсіз векторлар табылса, яғни
 ақырсыз өлшемді болса, онда
ақырсыз өлшемді болса, онда
 абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
Гильберт кеңістігінде элементінің нормасы
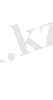
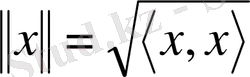
арқылы енгізіледі.
Бұл өрнекпен енгізілген
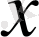 элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
Гильберт кеңістігінде
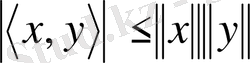
теңсіздігі орынды болады. Бұл теңсіздік Коши-Буняковский-Шварц теңсіздігі деп аталады.
Гильберт кеңістігінде метрика
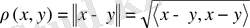
теңдігі бойынша анықталады және осы метрика мағынасында Н толық кеңістік болып табылады.
Егер
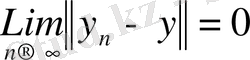 және
және
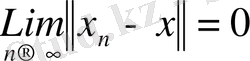 болса, онда
болса, онда
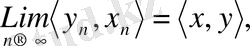
яғни скаляр көбейтіндінің үзіліссіздігі орынды.
Гильберт кеңістігіндегі ортогональдық.
Анықтама 3. 2.
Гильберт кеңістігінің
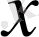 және
және
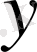 элементтері ортогональды деп аталады, егер
элементтері ортогональды деп аталады, егер
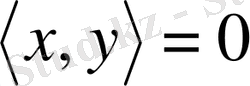 болса және
болса және
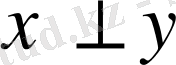 деп белгілейді.
деп белгілейді.
Егер
 үшін
үшін
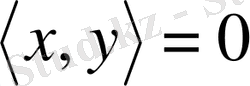 болса, онда
болса, онда
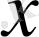 элементі
элементі
 жиынына ортогональ делінеді,
жиынына ортогональ делінеді,
 деп жазылады.
деп жазылады.
Теорема 3. 1.
Егер
 және
және
 болса, онда
болса, онда
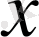 элементінің
элементінің
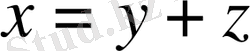 жіктелуі бар және ол жалғыз. Мұндағы
жіктелуі бар және ол жалғыз. Мұндағы
 ал
ал
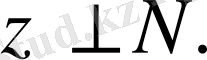
Салдар.
 кеңістігі ортогональды қосындыға жіктеледі, яғни
кеңістігі ортогональды қосындыға жіктеледі, яғни
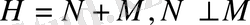
Лемма 3. 1.
 сызықты көпбейнесі
сызықты көпбейнесі
 кеңістігінде барлық жерде тығыз болу үшін
кеңістігінде барлық жерде тығыз болу үшін
 көпбейнесіне ортогональ нөлден өзгеше элементтің болмауы қажетті және жеткілікті
көпбейнесіне ортогональ нөлден өзгеше элементтің болмауы қажетті және жеткілікті
Дәлелдеуі:
Қажеттілігі:
Айталық
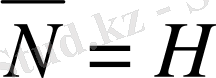 және
және
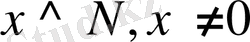 бар болсын
бар болсын
 , онда
, онда
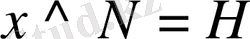 . Демек
. Демек
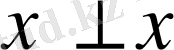 , олай болса
, олай болса

Жеткіліктілігі:
Айталық
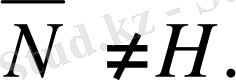 Олай болса
Олай болса
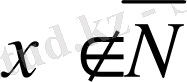 табылып, алдыңғы теорема бойынша
табылып, алдыңғы теорема бойынша
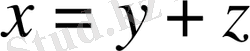 жіктелуі бар болады. Мұндағы
жіктелуі бар болады. Мұндағы
 , ал
, ал
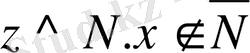 болғандықтан
болғандықтан
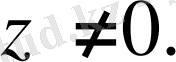 Ал бұл теорема шартына қайшы.
Ал бұл теорема шартына қайшы.
4. Сызықты операторлар теориясының элементтері.
Айталық
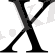 және
және
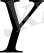 сызықты нормаланған кеңістіктер болсын.
сызықты нормаланған кеңістіктер болсын.
 жиынында
жиынында
 операторы анықталған дейді, егер әрбір
операторы анықталған дейді, егер әрбір
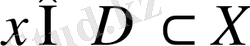 үшін
үшін
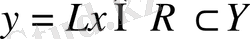 элементі сәйкес қойылса. Мұндағы
элементі сәйкес қойылса. Мұндағы
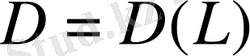 оператордың анықталу облысы, ал
оператордың анықталу облысы, ал
 оператордың мәндер облысы делінеді.
оператордың мәндер облысы делінеді.
Анықтама 4. 1.
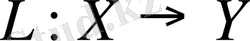 операторы сызықты деп аталады, егер
операторы сызықты деп аталады, егер
 және
және
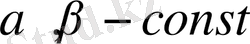 үшін
үшін
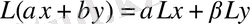 болса.
болса.
Анықтама 4. 2.
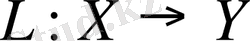 операторы шектелген деп аталады, егер
операторы шектелген деп аталады, егер
 үшін
үшін
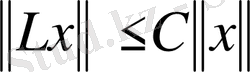 болатын С>0 тұрақтысы бар болса.
болатын С>0 тұрақтысы бар болса.
Осындай тұрақтылардың ең кішісі
 операторының нормасы делінеді де
операторының нормасы делінеді де
 деп белгіленеді.
деп белгіленеді.
Кез келген шектелген оператор үшін
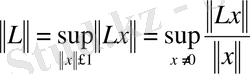
Анықтама 4. 3.
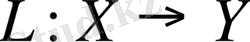 операторы үзіліссіз деп аталады, егер
операторы үзіліссіз деп аталады, егер
 болатын
болатын
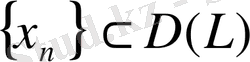 тізбегі үшін
тізбегі үшін
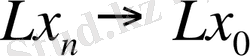 болса.
болса.
Теорема 4. 1.
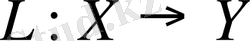 сызықты операторы шектелген болуы үшін оның үзіліссіз болуы қажетті және жеткілікті.
сызықты операторы шектелген болуы үшін оның үзіліссіз болуы қажетті және жеткілікті.
Анықтама 4. 4.
Айталық
 сызықты кеңістіктер және
сызықты кеңістіктер және
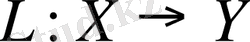 болсын.
болсын.
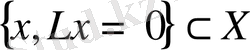 жиыны
жиыны
 операторының ядросы деп аталады және
операторының ядросы деп аталады және
 деп белгіленеді, яғни:
деп белгіленеді, яғни:
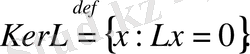
Нөл әрқашан сызықты оператордың ядросына енеді, яғни:
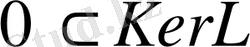 . Сызықты оператордың анықталу облысы, сондай-ақ мәндер облысытабиғаты әртүрлі жиындар болады.
. Сызықты оператордың анықталу облысы, сондай-ақ мәндер облысытабиғаты әртүрлі жиындар болады.
Анықтама 4. 5.
 сызықты кеңістігінде анықталған мәндер жиыны сандар болып келетін операторды функционал деп атаймыз.
сызықты кеңістігінде анықталған мәндер жиыны сандар болып келетін операторды функционал деп атаймыз.
Мысалы,
 жиыны -
жиыны -
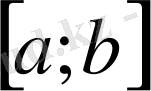 кесіндісінде анықталған өлшемді функциялардың жиыны болсын.
кесіндісінде анықталған өлшемді функциялардың жиыны болсын.
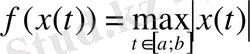 функционалы әрбір функцияға оның максимумын сәйкестендіреді.
функционалы әрбір функцияға оның максимумын сәйкестендіреді.
Анықтама 4. 6.
 функционалы сызықты деп аталады, егер ол келесі шартты қанағаттандырса:
функционалы сызықты деп аталады, егер ол келесі шартты қанағаттандырса:
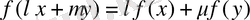 .
.
 гильберт кеңістігінде
гильберт кеңістігінде
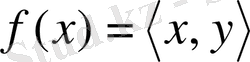 функционалын қарастырайық, мұндағы,
функционалын қарастырайық, мұндағы,
 кеңістігіндегі нөлден өзгеше бекітілген элемент.
кеңістігіндегі нөлден өзгеше бекітілген элемент.
Лемма 4. 1.
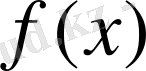 сызықты үзіліссіз функционал және
сызықты үзіліссіз функционал және
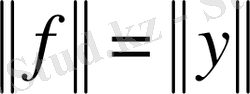
Дәлелдеуі:
Айталық
 , онда
, онда
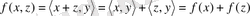
және
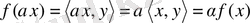 .
.
Коши теңсіздігінен

Сонымен
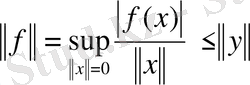 .
.
Басқа жағынан
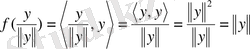 .
.
Бұдан
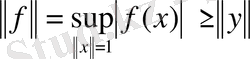 ,
,
яғни
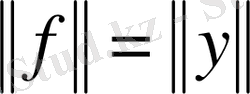
Сызықты үзіліссіз функционалдың нөлдерінің жиынын, яғни,
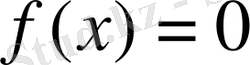 теңдеуінің түбірлерінің жиынын
теңдеуінің түбірлерінің жиынын
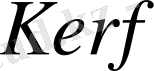 деп белгілейік.
деп белгілейік.
Лемма 4. 2
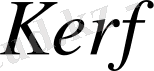 жиыны
жиыны
 кеңістігінің сызықты тұйық ішкі кеңістігі.
кеңістігінің сызықты тұйық ішкі кеңістігі.
5. Кері операторлар.
Айталық
 операторы
операторы
 кеңістігін
кеңістігін
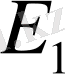 кеңістігіне түрлендірсін.
кеңістігіне түрлендірсін.
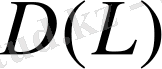 оператордың анықталу облысы, ал
оператордың анықталу облысы, ал
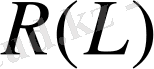 мәндер облысы.
мәндер облысы.
Анықтама 5. 1.
 операторы қайтымды деп аталады, егер
операторы қайтымды деп аталады, егер
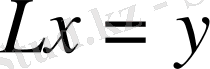 теңдеуінің жалғыз ғана шешімі бар болса.
теңдеуінің жалғыз ғана шешімі бар болса.
Егер L қайтымды болса, онда әрбір
 элементіне
элементіне
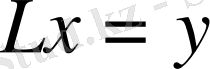 теңдеуінің шешімі болатындай бір ғана
теңдеуінің шешімі болатындай бір ғана
 элементін сәйкес қоюға болады. Осы сәйкестікті жасайтын операторды
элементін сәйкес қоюға болады. Осы сәйкестікті жасайтын операторды
 операторының кері операторы деп атайды және
операторының кері операторы деп атайды және
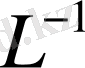 деп белгілейді.
деп белгілейді.
Айталық
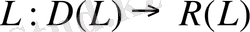 .
.
Теорема 5. 1.
Егер
 өзара бірмәнді бейнелеу болса, сонда тек сонда ғана
өзара бірмәнді бейнелеу болса, сонда тек сонда ғана
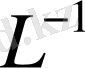 бар болады.
бар болады.
Кері оператордың бар болуы операторлар теориясында үлкен маңызды орын алады, Сондықтан «Қандай жағдайда кері оператор бар болады?»- сұрақ орынды.
Теорема 5. 2.
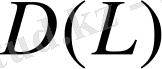 облысында анықталған
облысында анықталған
 сызықты операторы үшін
сызықты операторы үшін
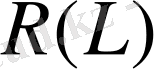 облысында анықталған кері
облысында анықталған кері
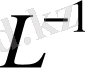 оператор бар болуы үшін
оператор бар болуы үшін
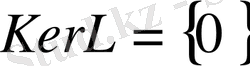 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
Оператор ядросының анықтамасы бойынша
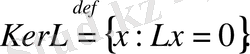 Демек
Демек
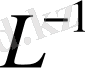 операторы бар болуы үшін
операторы бар болуы үшін
 біртекрі теңдеуінің тек
біртекрі теңдеуінің тек
 деген шешімінен басқа шешімнің жоқ болуы қажетті және жеткілікті.
деген шешімінен басқа шешімнің жоқ болуы қажетті және жеткілікті.
Дәлелдеуі:
Айталық
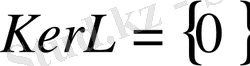 . Кері жориық.
. Кері жориық.
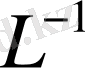 жоқ болсын. Онда
жоқ болсын. Онда
 түбірлеріне сәйкес келетін бір ғана
түбірлеріне сәйкес келетін бір ғана
 табылады. Бұдан оператордң сызықты екенін пайдалансақ
табылады. Бұдан оператордң сызықты екенін пайдалансақ
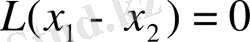 . Бұл теңдік
. Бұл теңдік
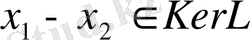 екенін білдіреді. Алайда
екенін білдіреді. Алайда
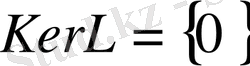 болғандықтан
болғандықтан
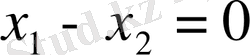 , бұдан
, бұдан
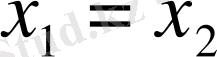 .
.
Айталық
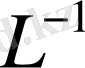 бар болсын және
бар болсын және
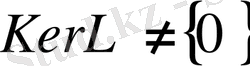 . Онда
. Онда
 .
.

 табылсын, яғни
табылсын, яғни
 .
.
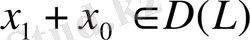 .
.
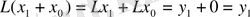 .
.
Соңғы теңдіктен
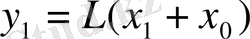 ,
,
 екенін аламыз. Бұл
екенін аламыз. Бұл
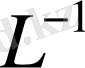 бар деген тұжырымға қайшы. Теорема дәлелденді.
бар деген тұжырымға қайшы. Теорема дәлелденді.
Теорема 5. 3.
Айталық
 сызықты кеңістіктер және
сызықты кеңістіктер және
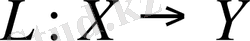 ,
,
 - сызықты оператор болсын. Егер
- сызықты оператор болсын. Егер
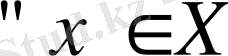 үшін
үшін
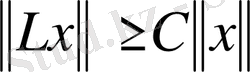 (C>0) болса, онда
(C>0) болса, онда
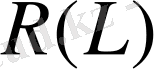 облысында шектеулі кері оператор бар болады.
облысында шектеулі кері оператор бар болады.
Дәлелдеуі: Келесі өзекті түсінікті енгізейік.
Анықтама
5. 2.
Егер
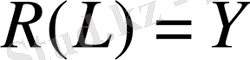 және шектеулі
және шектеулі
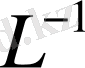 бар болса онда
бар болса онда
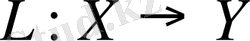 с
ызықты операторы үзіліссіз қайтымды деп аталады.
с
ызықты операторы үзіліссіз қайтымды деп аталады.
Теорема 5. 4.
 - үзіліссіз қайтымды болу үшін
- үзіліссіз қайтымды болу үшін
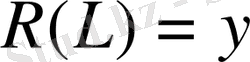 және
және
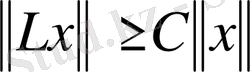 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
Бұл жұмыста біз тек сызықты оператормен жұмыс істейтін болғандықтан бізге келесі тұжырым қажет болады.
Теорема 5. 5.
 - сызықты оператор және оның анықталу облысы
- сызықты оператор және оның анықталу облысы
 кеңістігінде тығыз болсын.
кеңістігінде тығыз болсын.
 операторы үзіліссіз қайтымды болады, егер
операторы үзіліссіз қайтымды болады, егер
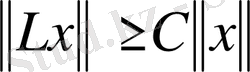 , (C>0),
, (C>0),
 теңдігімен қатар
теңдігімен қатар
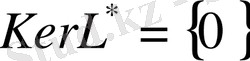 теңдігі орындалса.
теңдігі орындалса.
Дәлелдеуі:
Шектелген
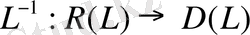 операторларының бар болатыны көрініп тұр.
операторларының бар болатыны көрініп тұр.
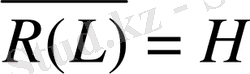 екенін көрсетейік. Кері жориық.
екенін көрсетейік. Кері жориық.
 . Онда Рисс теоремасы бойынша
. Онда Рисс теоремасы бойынша
 ,
,
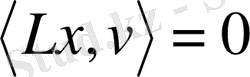 . Бұдан
. Бұдан
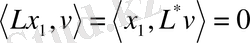 .
.
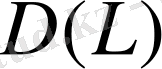 жиыны
жиыны
 кеңістігінде тығыз болғандықтан
кеңістігінде тығыз болғандықтан
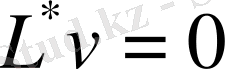 . Бұл
. Бұл
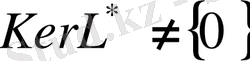 екенін білдіреді. Біз қайшылыққа келдік. Теорема дәлелденді.
екенін білдіреді. Біз қайшылыққа келдік. Теорема дәлелденді.
6.
 кеңістігі.
кеңістігі.
 белгісі арқылы
белгісі арқылы
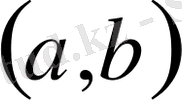 -да өлшемді,
-да өлшемді,
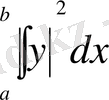 интегралы ақырлы болатын
интегралы ақырлы болатын
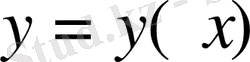 функциялар жиынын белгілейміз.
функциялар жиынын белгілейміз.
егер
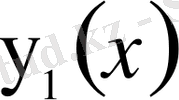 және
және
 функциялары тек нөлдік өлшемді жиында ғана әртүрлі болса, онда олар тең деп қарастырылады. Мұнда өлшем мен интеграл Лебег мағынасында қарастырылады.
функциялары тек нөлдік өлшемді жиында ғана әртүрлі болса, онда олар тең деп қарастырылады. Мұнда өлшем мен интеграл Лебег мағынасында қарастырылады.
Егер
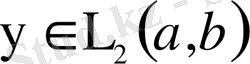 болса, онда у функциясы үшін
болса, онда у функциясы үшін
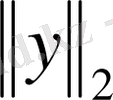 нормасы келесідей анықталады:
нормасы келесідей анықталады:
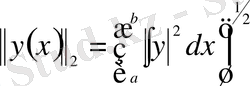 .
.
Бұл норма мынадай қасиеттерге ие:
1)
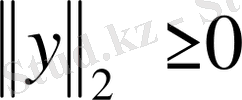 барлық у үшін,
барлық у үшін,
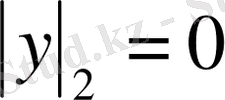 және
және
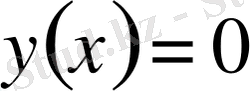 шарттары эквивалентті;
шарттары эквивалентті;
2)
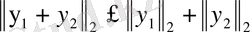
3)
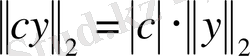 , мұндағы с - константа.
, мұндағы с - константа.
Егер қайсыбір
 тегі
тегі
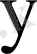 және
және
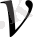 функцияларының ара қашықтығы
функцияларының ара қашықтығы
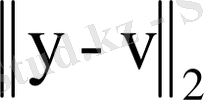 түрінде анықталса, онда
түрінде анықталса, онда
 метрикалық кеңістік болады.
метрикалық кеңістік болады.
 кеңістігі толық метрикалық кеңістік болады. Бұдан егер
кеңістігі толық метрикалық кеңістік болады. Бұдан егер
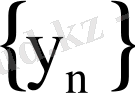 фундаментальды кеңістік болса, яғни
фундаментальды кеңістік болса, яғни
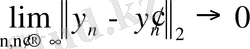 , онда
, онда
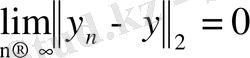 орындалатындай жалғыз
орындалатындай жалғыз
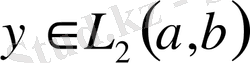 функциясы табылады.
функциясы табылады.
Осыдан норманың келесі (үзіліссіздік) қасиеті шығады: егер
 нормасында
нормасында
 болса, онда
болса, онда
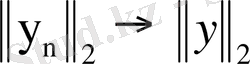 .
.
Сонымен қатар,
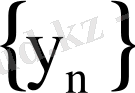 тізбегінің
тізбегінің
 -ке барлық жерде дерлік жинақталатын ішкі тізбегі болады.
-ке барлық жерде дерлік жинақталатын ішкі тізбегі болады.
 кеңістігінің келесі қасиеттерін қарастырайық:
кеңістігінің келесі қасиеттерін қарастырайық:
1)
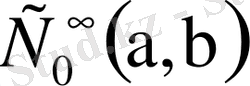 жиыны
жиыны
 -да толық болады, мұндағы
-да толық болады, мұндағы
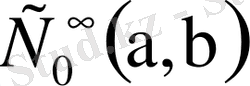 жиыны
жиыны
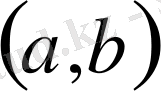 -да шексіз дифференциалданатын, финитті функциялар жиыны.
-да шексіз дифференциалданатын, финитті функциялар жиыны.
Бұдан әрбір
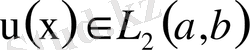 элементі үшін
элементі үшін
 -ға жинақталатын
-ға жинақталатын
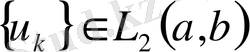 тізбегі табылатыны шығады.
тізбегі табылатыны шығады.
2)
 кеңістігі сепарабельді, яғни бұл кеңістікте барлық жерде толық саналымды жиын бар.
кеңістігі сепарабельді, яғни бұл кеңістікте барлық жерде толық саналымды жиын бар.
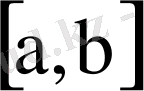 кесіндісіндегі кез келген үзіліссіз функцияны
кесіндісіндегі кез келген үзіліссіз функцияны
 нормасы бойынша көпмүшеліктер тізбегіне жуықтатуға болатыны белгілі. Онда, жоғары айтылғандардан, рационал коэффициентті көпмүшеліктердің саналымды жиыны
нормасы бойынша көпмүшеліктер тізбегіне жуықтатуға болатыны белгілі. Онда, жоғары айтылғандардан, рационал коэффициентті көпмүшеліктердің саналымды жиыны
 -да барлық жерде толық болатыны анық
-да барлық жерде толық болатыны анық
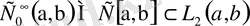 .
.
3) Коши теңсіздігі орындалады: айталық
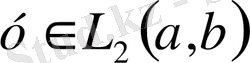 ,
,
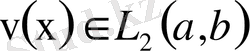 болсын. Онда
болсын. Онда
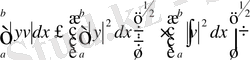 (1)
(1)
орындалады.
Егер
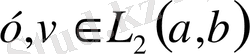 болса, онда (1) ден
болса, онда (1) ден
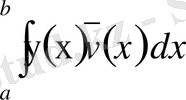 интегралы анықталған және ақырлы.
интегралы анықталған және ақырлы.
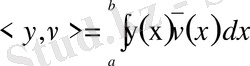 қатынасы
қатынасы
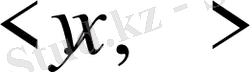 түрінде анықталатын
түрінде анықталатын
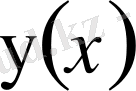 және
және
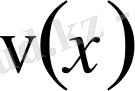 функцияларының
функцияларының
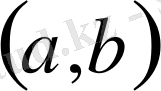 -дағы скаляр көбейтіндісін анықтайды. Скаляр көбейтінді келесі қасиеттерге ие:
-дағы скаляр көбейтіндісін анықтайды. Скаляр көбейтінді келесі қасиеттерге ие:
- барлық у үшін, алболса, онда(элементі ретінде) ; ;, мұндағы- тұрақтылар; ; (Коши-Буняковский теңсіздігі) Егержәне, онда
7.
кеңістігі.
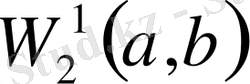 кеңістігі арқылы бірінші ретті жалпыланған туындысы бар және бірінші ретті жалпыланған туындысымен бірге өздері де
кеңістігі арқылы бірінші ретті жалпыланған туындысы бар және бірінші ретті жалпыланған туындысымен бірге өздері де
 кеңістігінде жататын функциялардың ішкі жиынын белгілейік.
кеңістігінде жататын функциялардың ішкі жиынын белгілейік.
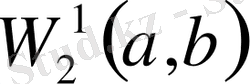 кеңістігі - сызықты. Оның скалярлық көбейтіндісі
кеңістігі - сызықты. Оның скалярлық көбейтіндісі
(1)
болатын Гильберт кеңістігі екенін дәлелдейік.
(1) өрнегі скалярлық көбейтіндінің барлық аксиомаларын қанағаттандыратыны оңай дәлелденеді.
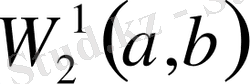 кеңістігі келесі скалярлық көбейтінді бойынша толық болатынын дәлелдейік:
кеңістігі келесі скалярлық көбейтінді бойынша толық болатынын дәлелдейік:
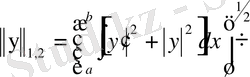 (2)
(2)
Айталық,
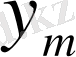
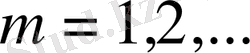 - элементтері
- элементтері
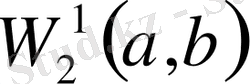 -ден алынған (2) нормасы бойынша фундаментальды тізбек болсын:
-ден алынған (2) нормасы бойынша фундаментальды тізбек болсын:
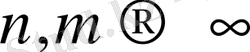 болғанда,
болғанда,
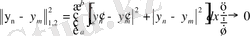 .
.
Онда
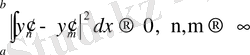 (3)
(3)
және
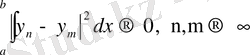 (4)
(4)
 толық болғандықтан, (4) -тен
толық болғандықтан, (4) -тен
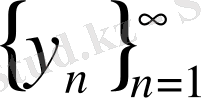 тізбегі
тізбегі
 нормасы бойынша жинақталатын
нормасы бойынша жинақталатын
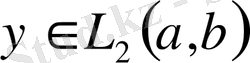 функциясы болатыны шығады. Ал (1. 6. 3) -тен
функциясы болатыны шығады. Ал (1. 6. 3) -тен
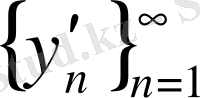 тізбегі
тізбегі
 нормасы бойынша жинақталатындай,
нормасы бойынша жинақталатындай,
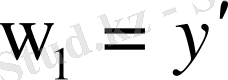 функциясы табылатыны шығады.
функциясы табылатыны шығады.
Әрбір
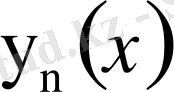 функциясының
функциясының
 -дегі бірінші ретті жалпыланған туындысы болатындықтан, кез келген
-дегі бірінші ретті жалпыланған туындысы болатындықтан, кез келген
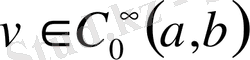 үшін келесі теңдік орындалады:
үшін келесі теңдік орындалады:
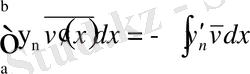 .
.
Бұл теңдікте
 шегіне көше отырып,
шегіне көше отырып,
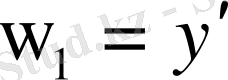 функциясы
функциясы
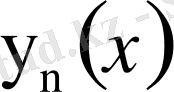 функциясының бірінші жалпыланған туындысы екендігіне көз жеткіземіз. Олай болса,
функциясының бірінші жалпыланған туындысы екендігіне көз жеткіземіз. Олай болса,
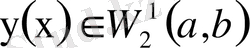 . Тұжырым дәлелденді.
. Тұжырым дәлелденді.
8. Түйіндес операторлар.
Е
сызықты кеңістігін
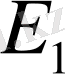 кеңістігіне түрлендіретін
L
операторын қарастырайық. g функционалы
кеңістігіне түрлендіретін
L
операторын қарастырайық. g функционалы
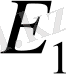 кеңістігінде анықталсын, яғни
кеңістігінде анықталсын, яғни
 Осы функционалды
Осы функционалды
 элементіне қолданайық:
элементіне қолданайық:
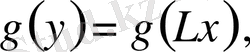 яғни
яғни
 (Мұндағы
(Мұндағы
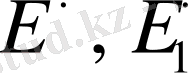 сәйкесінше
Е,
сәйкесінше
Е,
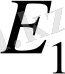 кеңістіктеріне түйіндес кеңістіктер) . Демек, әрбір
кеңістіктеріне түйіндес кеңістіктер) . Демек, әрбір
 функционалына
функционалына
 функционалын сәйкес қойдық.
функционалын сәйкес қойдық.
Анықтама 8. 1.
Жоғарыдағы әдіспен анықталған сәйкестікті
L
операторына түйіндес оператор деп атап,
 деп белгілейміз.
деп белгілейміз.
f
функционалының
х
элементіндегі мәнін
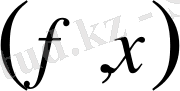 деп белгілесек, онда
деп белгілесек, онда
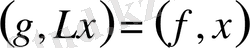 немесе
немесе
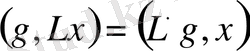 екенін аламыз.
екенін аламыз.
Түйіндес оператордың қасиеттері:
- егерLсызықты болса, ондаоператоры да сызықты болады;
- ;
- ;
- егерLүзіліссіз болса, ондаоператоры да үзіліссіз болады;
- , мұндағыбірлік оператор.
Теорема 8. 1.
Егер
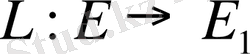 шектелген сызықты оператор болса, онда
шектелген сызықты оператор болса, онда
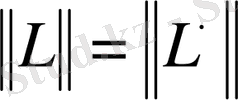 (
Е
және
(
Е
және
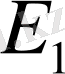 Банах кеңістіктері) .
L
операторы
Банах кеңістіктері) .
L
операторы
 Гильберт кеңістігінде анықталған болса, Рисс теоремасы бойынша түйіндес оператордың анықтамасы
Гильберт кеңістігінде анықталған болса, Рисс теоремасы бойынша түйіндес оператордың анықтамасы
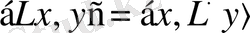 түрінде болады.
түрінде болады.
L
және
 операторлары бір кеңістікте анықталатын жағдайлар көп кездеседі. Осындай жағдайда
операторлары бір кеңістікте анықталатын жағдайлар көп кездеседі. Осындай жағдайда
 операторы жақсы қасиетке ие болады.
операторы жақсы қасиетке ие болады.
Анықтама 8. 2.
 ішкі кеңістігі
L
операторына қатысты инвариантты деп аталады, егер
ішкі кеңістігі
L
операторына қатысты инвариантты деп аталады, егер
 үшін
үшін
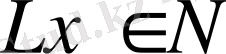 болса.
болса.
Теорема 8. 2.
 ішкі кеңістігі
L
операторына қатысты инвариантты болса, онда
ішкі кеңістігі
L
операторына қатысты инвариантты болса, онда
 ортогональді толықтауышы
ортогональді толықтауышы
 операторына қатысты инвариантты болады.
операторына қатысты инвариантты болады.
Дәлелдеуі:
Егер
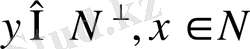 болса, онда
болса, онда
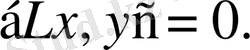 Бұдан түйіндес оператордың анықтамасы бойынша
Бұдан түйіндес оператордың анықтамасы бойынша
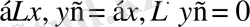 . Демек,
. Демек,
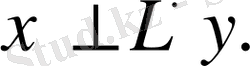 Олай болса,
Олай болса,
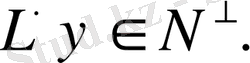
Айталық,
 болсын.
болсын.
 түйіндес операторы
түйіндес операторы

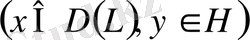 теңдеуінің шешімінің бар екенін көрсетуде зор рөл ойнайды.
теңдеуінің шешімінің бар екенін көрсетуде зор рөл ойнайды.
Теорема 8. 3.
 теңдеуінің
теңдеуінің
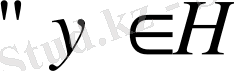 үшін бір ғана шешімі бар болады, сонда тек сонда ғана, егер
үшін бір ғана шешімі бар болады, сонда тек сонда ғана, егер
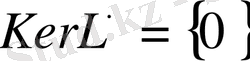 болса.
болса.
Түйіндес оператор түсінігін шектеусіз операторлар жағдайына да келтіруге болады. Мұны гильбертті кеңістік жағдайын қарастырайық.
А-Н гильбертті кеңістігінде толығынан анықталған сызықты оператор болсын.
 - барлық
- барлық

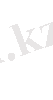 үшін
үшін
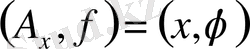
болатындай
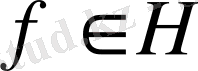 жиыны, мұнда
жиыны, мұнда
 .
.
Әр
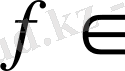
 үшін
үшін
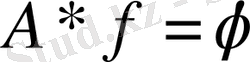 деп алайық.
деп алайық.
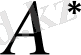 операторы А -ға түйіндес деп аталады.
операторы А -ға түйіндес деп аталады.
Атап, кетуіміз керек,
 - (1. 9. 2) формуласы бойынша бір мәнді болып анықталуы үшін
- (1. 9. 2) формуласы бойынша бір мәнді болып анықталуы үшін
 облысы тығыз болуы қажет.
облысы тығыз болуы қажет.
9. Тұйық операторлар.
Математиканың әртүрлі сұрақтарын қарастыруда аддитивті, біртекті, бірақ шенелмеген операторларға кез боламыз. Мұндай операторлар қатарына математика үшін маңызды дифференциалды операторлар жатады. Алайда бұл операторларды тұйық операторларға дейін кеңейтуге болады.
Айталық.
 нормаланған кеңістіктер және
нормаланған кеңістіктер және
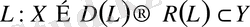 болсын.
болсын.
Анықтама 9. 1.
L
операторы тұйық деп аталады, егер
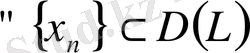 үшін
үшін
 және
және
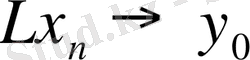 қатыстарынан
қатыстарынан
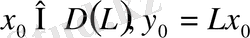 қатыстары орындалса.
қатыстары орындалса.
Үзіліссіз операторлар тұйық болады, ал кері тұжырым әрқашан орынды емес.
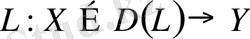 сызықты операторы тұйық емес болсын. Бұл жағдайда оның
сызықты операторы тұйық емес болсын. Бұл жағдайда оның
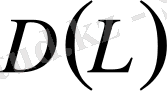 анықталу облысын кеңейту арқылы тұйықтауға болады. Мұндай операторлар тұйықталатын деп аталады.
анықталу облысын кеңейту арқылы тұйықтауға болады. Мұндай операторлар тұйықталатын деп аталады.
Төменде тұйықталған оператордың осы анықтамасына эквивалентті анықтамасын келтірейік, ол үшін оператор графигі деген түсінік пайдаланатын болады.
Анықтама 9. 2.
 және
және
 -нормалданған кеңістіктер болсын. Онда
-нормалданған кеңістіктер болсын. Онда
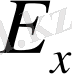 *
*
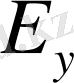 =
=
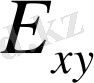 көбейтіндісі
көбейтіндісі
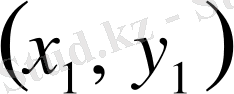 +
+
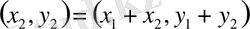 ;
;
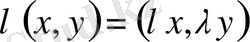 амалдарыменен (операцияларыменен) сызықты кеңістік болады. Мұнда егер
амалдарыменен (операцияларыменен) сызықты кеңістік болады. Мұнда егер
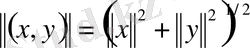 деп алатын болсақ, онда
деп алатын болсақ, онда
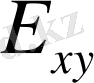 нормалданған кеңістік болады. Бұл кеңістік толық болады, егерде
нормалданған кеңістік болады. Бұл кеңістік толық болады, егерде
 және
және
 толық кеңістіктер болатын болса, өйткені
толық кеңістіктер болатын болса, өйткені
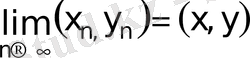 болады тек сонда ғана, егерде
болады тек сонда ғана, егерде
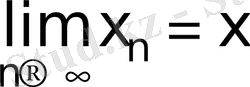 және
және
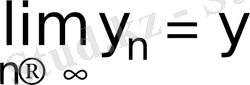 болса.
болса.
Теорема 9. 1.
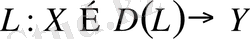 сызықты операторы тұйықталатын болуы үшін
сызықты операторы тұйықталатын болуы үшін
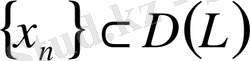 ,
,
 және
және
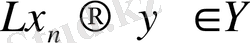 шарттарынан
шарттарынан
 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
II. ТАРАУ. Тербелістер теңдеуі. (Ішектің тербеліс теңдеуін қорытып шығару. Шексіз ішек. Даламбер формуласы. Фурье әдісі. )
Тербелмелі қозғалыстармен байланысты физикалық есептерде екінші реттік гиперболалық теңдеулер типі кездеседі. Гиперболалық теңдеудің жай түрі:
U xx -U yy =0 (1)
кейде оны ішектің тербеліс теңдеуі деп атайды.
Ішектің ұзындығының кез- келген нүктесін х абсциссадағы мәні арқылы сипаттауға болады. Ішектің орын ауыстыруы (х, ) біртекті жазықтығында жатыр деп, ал ығысу векторын х осіне кез- келген мезетте перпендикуляр деп, онда тербелу процесін бір функция арқылы сипаттауға болады. Ішек ретінде мықты серпімді жіп алынады. Ішекте пайда болатын кернеу үздіксіз профиліне жанама бойымен бағытталады. Созу шамасы серпімділікке байланысты Гук заңы бойынша анықталады. Созылу кезіндегі иілген бөлігі:
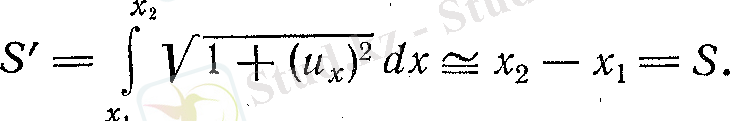 (2)
(2)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz