Кинематика туралы ұғым

Жоспар
Кіріспе

§1. Жалпы ескертпелер
§2. Түзу сызықты бір қалыпты қозғалыс
§ 3. Түзу сызықты айнымалы қозғалыс
§4. Тузу сызықты бір қалыпты айнымалы қозғалыс. Үдеу
§5. Кез келген түзу сызықты қозғалыстың үдеуі
§6. Жылдамдық және үдеу — векторлар
§7. Қисық сызықты қозғалыс.
§8. Қисық сызықты қозғалыстың үдеуі
§9. Қатты дененің кинематикасы. Бұрыштық жылдамдық пен үдеу
§10. Бұрыштық жылдамдық — вектор

Механика дегеніміз — материя қозғалысының ең жай формасы туралы ілім, яғни денелердің немесе олардың жеке бөліктерінің бір-бірімен салыстырғанда орын ауыстыруы жайындағы ілім.
Механика қағидалары да, басқа жаратылыс ғылымдарынікі сияқты, тәжірибе деректерін талдап қорыту арқылы тағайындалады. Денелердің орын ауыстыруы жайындағы тәжірибелер ең оңай тәжірибелерге жатады. Адам денелердің орын ауыстыруын күнделікті тіршілігінде, кез келген өндіріс процестерінде күнбе-күн көріп-бақылап отырады, механикалық ұғымдардың көрнекі болуы да осыдан. Барлық жаратылыс ғылымдарының ішінде механиканың алдымен өрістеп дамуының да себебі осы болады. Механиканың негізгі заңдарын ашып анықтауда Галилей (1564-1642) едәуір еңбек сіңірген, оларды Ньютон (1642-1727) тұжырымды түрде баяндады. Петербург Ғылым академиясында көп жыл бойы қызмет істеген Леонард Эйлер (1707-1783) тұңғыш рет механика заңдарын аналитикалық түрге келтірді, механиканың дамуына ат салысып, үлкен роль атқарды. Алайда «классикалық» механика деп аталатын Галилей — Ньютон механикасы тек козғалыстың санаулы түрлерін ғана бақылау нәтижесінде шықты, атап айтқанда, өлшемдері адам денесінің үлкендігімен шамалас денелердің (түскен тастың) немесе оған қарағанда өте үлкен денелердің (планеталардың) жылдамдығы бәсең қозғалыстарын зерттеу нәтижесінде шықты. Классикалық механиканың жуық болу себебі де осыдан. Ғылым дами келе, классикалық механиканың тек өте көп атомдардан құралған денелердің (макроскопиялық денелердің) қозғалысын қарастырғанда және олардың жылдамдығы жарық жылдамдығынан гөрі аз болғанда ғана шындыққа дұрыс келетіндігі байқалды. Ленин: «...механика реалды баяу қозғалыстардың суреті екені, ал жаңа физика орасан жылдам реалды қозғалыстардың суреті екені күмәнсыз болып отыр» деген.

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

КИНЕМАТИКА
§4. Жалпы ескертпелер. Механика дегеніміз — материя қозғалысының ең жай
формасы туралы ілім, яғни денелердің немесе олардың жеке бөліктерінің бір-
бірімен салыстырғанда орын ауыстыруы жайындағы ілім.
Механика қағидалары да, басқа жаратылыс ғылымдарынікі сияқты, тәжірибе
деректерін талдап қорыту арқылы тағайындалады. Денелердің орын ауыстыруы
жайындағы тәжірибелер ең оңай тәжірибелерге жатады. Адам денелердің орын
ауыстыруын күнделікті тіршілігінде, кез келген өндіріс процестерінде күнбе-
күн көріп-бақылап отырады, механикалық ұғымдардың көрнекі болуы да осыдан.
Барлық жаратылыс ғылымдарының ішінде механиканың алдымен өрістеп дамуының
да себебі осы болады. Механиканың негізгі заңдарын ашып анықтауда Галилей
(1564-1642) едәуір еңбек сіңірген, оларды Ньютон (1642-1727) тұжырымды
түрде баяндады. Петербург Ғылым академиясында көп жыл бойы қызмет істеген
Леонард Эйлер (1707-1783) тұңғыш рет механика заңдарын аналитикалық түрге
келтірді, механиканың дамуына ат салысып, үлкен роль атқарды. Алайда
классикалық механика деп аталатын Галилей — Ньютон механикасы тек
козғалыстың санаулы түрлерін ғана бақылау нәтижесінде шықты, атап айтқанда,
өлшемдері адам денесінің үлкендігімен шамалас денелердің (түскен тастың)
немесе оған қарағанда өте үлкен денелердің (планеталардың) жылдамдығы бәсең
қозғалыстарын зерттеу нәтижесінде шықты. Классикалық механиканың жуық болу
себебі де осыдан. Ғылым дами келе, классикалық механиканың тек өте көп
атомдардан құралған денелердің (макроскопиялық денелердің) қозғалысын
қарастырғанда және олардың жылдамдығы жарық жылдамдығынан гөрі аз болғанда
ғана шындыққа дұрыс келетіндігі байқалды. Ленин: ...механика реалды баяу
қозғалыстардың суреті екені, ал жаңа физика орасан жылдам реалды
қозғалыстардың суреті екені күмәнсыз болып отыр деген.
Жылдамдықтары жарық жылдамдығымен шамалас макроскопиялық денелердің
қозғалыс заңдары Эйнштейн шығарған салыстырмалылық теориясында
тағайындалады.
Жеке атомдардың немесе элементар бөлшектердің (микроскопиялық
денелердің) қозғалыстарын қарастырғанда да классикалық механиканың заңдары
дұрыс келмейді. Микроскопиялық денелердің қозғалыс заңдары кванттық
механикада тағайындалады. Классикалық механиканың қолданылу шектерін
кейінірек көрсетеміз. Қазірше сөз тек жылдамдығы жарық жылдамдығына
қарағанда едәуір аз макроскопиялық денелер қозғалысы туралы ғана болып отыр
деп ұйғарамыз.
Механикалық құбылыстардың үйреншікті, көрнекі болуы және кейбір
физикалық құбылыстарды (мысалы, дыбыс құбылыстарын) тек механикалық ұғымдар
арқылы ғана түсіндіру табыстары мынаған алып келіп соқты: XIX ғасырда көп
физиктер үшін бір құбылысты түсіндіру — оны механикалық құбылыстарға
келтіру болып табылды. Мұндай көзкарас философиялық механикалық материализм
талабына сай болды. Алайда физиканың одан әрі дамуы, әсіресе жарық пен
электр туралы ілімдердің дамуы, көп құбылыстардың өзінің меншікті заңдарына
бағынатындығын және оларды қозғалыстың жай түріне — механикалық қозғалысқа
келтіруге болмайтындығын көрсетті. Механикалық материализм өзінің орнын
диалектикалық материализмге беруге тиісті болды, диалектикалық материализм
болса материя қозғалысының жалпы түрлерін карастырады, нақты дүниенің түрлі-
түрлі жақтарын есепке алады.
Энгельс бұл туралы былай деп жазған: Табиғатты зерттеушілер
қозғалысты, ұдайы механикалық қозғалыс, орын ауыстыру деп қана
қарастырады... Материяға қолданғанда қозғалыс дегеніміз жалпы өзгеріс
болады. Осы сияқты жаңылысудан барлық нәрсені механикалық қозғалысқа
келтіруге өршелене тырмысу келіп шығады, ол қозғалыстың басқа формаларының
ерекше сипаттарын көмескі етеді.
Механикалық қозғалыс мейлінше күрделі болып келуі және оның сан алуан
түрлері болуы мүмкін. Сондықтан механикада нақты қозғалысты жай
қозғалыстарға жіктейді, оларды зерттейді де қайтадан күрделірек
козғалыстарға көшеді. Материялық нүктенің қозғалысы ең жай механикалық
қозғалыс болып табылады. Механикада материялық нүкте деп берілген есепте
үлкендігі мен формасын елемеуге балатын денені айтады. Нақты бір дененің
өзін есептің шартына қарай материялық нүкте деп немесе шектелген өлшемі бар
дене деп қарастыру жиі кездеседі. Мысалы, артиллерия снарядының ұшуы туралы
есеп шығарғанда, жуықтап алғанда, оның формасы мен үлкендігін елеместен,
снарядты материялық нүкте деп қарастыруымызға болады. Егер снарядтың ұшуына
ауаның кедергісінің ететін әсерін және ұшып бара жатқандағы айналыстың
ролін есепке алу қажет болса, онда снарядты материялық нүкте деп
қарастыруға болмайды: біз оның формасын, үлкендігін т. т. есепке алуымыз
керек. Сонымен қатар астрономдар жер шарының өз орбитасының бойымен Күнді
айнала козғалуын қарастырғанда, оларға жер шарын материялық нүкте деп
санауға болады.
Берілген анықтама бойынша механикалық қозғалыс дегеніміз жай орын
ауыстыру болады, ал бір дене басқа материялық денелермен салыстырғанда ғана
орын ауыстыра алады. Сондықтан бір дененің қозғалысын сипаттауға мүмкіндік
жасау үшін алдымен қандай денемен (немесе бір-бірімен салыстырғанда
қозғалмайтын бір топ денемен) салыстыра отырып, берілген дененің орын
ауыстыруын есептейміз, соған келісіп алуымыз керек. Сол дене (немесе
денелер) санау системасы болып табылады. Сонымен әрбір қозғалысты - белгілі
бір санау системасымен салыстырып қарастыруымыз керек. Түрлі жағдайларда
санау системасын түрліше тәсілмен сайлап алуға болады, бірақ санау
системасын тиянақты етіп сайлап алған соң ғана, біз берілген қозғалысты
анық сипаттай аламыз. Мысалы, біз бір нәрсені тастап жіберіп, оның
қозғалысын бөлмемен салыстырып қарастыруымызға болады; бұл жағдайда
бөлменің едені, қабырғалары және басқа жерлері санау системасын береді. Ал
біз осы дененің қозғалысын Күнмен немесе бір белгілі жұлдызбен салыстырып
қарастыруымызға да болады. Бірақ алынған нәрсенің қозғалысын немен
салыстырып қарастырамыз, соған алдын ала мықтап келісіп алуымыз керек.
Практикада қозғалысты сипаттау үшін санау системасын құрайтын денелерге
бір координаталар системасын, мысалы кәдімгі түзу сызықты тік бұрышты
координаталар системасын, байланыстыруға тура келеді. Қозғалысты бөлмемен
салыстырып қарағанда, мысалы, координаталардың басын бөлменің бір бұрышына
орналастырып, осьтерін қабырғалардың бойымен бағыттауға болады; немесе
координаталар системасының басын Күнге орналастырып, осьтерін белгілі
жұлдыздарға қарай жүргізуге болады. Алдағы жерде біз санау системасын
сайлап алу туралы мәселе қарастырамыз, ал қазірше біз санау системасы
әрқашанда мәлім және оған байланыстырған координаталар системасы берілген
деп аламыз, оны қозғалысты сипаттау үшін пайдаланамыз.
Механиканы әдетте кинематика және динамика деген екі бөлімге бөледі:
кинематикада дененің тек уақытқа байланысты орын ауыстыруы ғана
қарастырылады; динамикада дененің қозғалыс күйін өзгеріске ұшырататын
денелердің өз ара әсерлері есепке алынады.
§5. Түзу сызықты бір қалыпты қозғалыс. Материялық нүкте деп ұйғарылған
дененің қозғалысын, яғни оның OD түзуінің (1-сурет) бойымен бір қалыпты
орын ауыстыруын қарастырайық. Кез келген t уақыт кезеңінде қозғалған
дененің А нүктесіне келгендегі орнын s кесіндісі арқылы анықтай аламыз; ол
кесінді санаудың басы етіп алынған О нүктесінен басталып есептелінеді.
Әрине, s уақытқа байланысты өзгереді. Егер бастапқы кезде (t=0) дене О
нүктесінде тұрған болса, онда s кесіндісі дұрысында түзу сызықтың бойымен
қозғалған дененің жолымен дәл келеді. OXYZ координаталар системасын сызып,
берілген бір уақыт кезеңіндегі дененің орнын оның х, у, z координаталары
арқылы сипаттауға да болады. Координаталар системасын, 1-суреттегідей етіп,
сайлап алғанда, дененің х, у, z координаталары жолдың координата осьтеріне
түсірілген sx, sy, sz проекцияларына дәл келеді, Сонымен, қозғалған
нүктенің орнын s кесіндісі арқылы сипаттауға болады, сонда ол t уақытының
функциясы болып табылады:

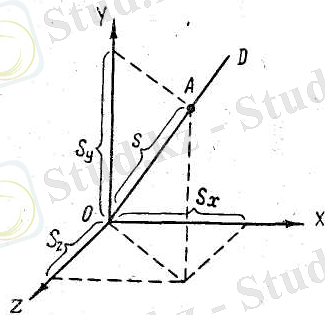
1-сурет. Түзу сызықты қозғалыс кезінде А денесінің орны не s кесіндісі
арқылы, не оның координаталар осьтеріне түсірілген sx, sy sz проекциялары
арқылы анықталады.

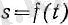(1)
немесе сол нүктенің х, у, z координаталары арқылы сипаттауға болады, олар
да уақыттың функциялары болады:
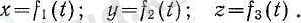(2)
Қарастырылған жағдайда дене түзудің бойымен қозғалатын болғандықтан,
қозғалыс түзу сызықты қозғалыс деп аталады.
Егер қозғалған дене кез келген өз ара тең уақыт аралықтарында бірдей
жол жүрсе, ондай қозғалыс бір қалыпты қозғалыс деп аталады.
Әрине, қозғалыстардың бірінен бірінің айырмашылығы болады, өйткені әр
түрлі денелер бірдей уақыт аралықтары ішінде түрліше жол жүруі мүмкін,
басқа сөзбен айтқанда, түрліше уақыт аралықтары ішінде бірдей жол жүруі
мүмкін. Қозғалыстардың осындай айырмашылығын біз жылдамдық деген ұғым
енгізу арқылы сипаттаймыз. Бір қалыпты қозғалыстың жылдамдығы дегеніміз —
физикалық шама, сонда дене берілген уақыт аралығында неғұрлым көп жол
жүрсе, ол шама соғұрлым үлкен болады, басқа сөзбен айтқанда, берілген жолды
жүруге керек уақыт неғұрлым аз болса, ол шама соғұрлым зор болады. Сонымен,
бір қалыпты қозғалыстың v жылдамдығы деп, жүрілген жолға тура пропорционал,
сол жолды жүруге кеткен уақытқа кері пропорционал болып келген физикалық
шаманы айтады.
Мысалы, түзу сызықпен бір қалыпты қозғалған дененің орны t0 уақыты
кезеңінде s0 кесіндісі арқылы; t уақыты кезеңінде s кесіндісі арқылы
анықталған болсын. Сонда t - to уақыты ішінде дене s – s0 жол жүреді де, v
жылдамдығының математикалық өрнегі мынадай болады:
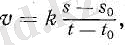(3)
мұндағы k — пропорционалдық коэффициент. Дербес жағдайда, егер t0 = 0 және
s0 = 0 болса, онда
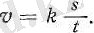(3а)
Сонда s дегеніміз t уақыты ішінде жүрілген жол болады. Бір қалыпты
қозғалыстың жылдамдығы — тұрақты шама. (3) теңдікпен пайдаланып кез келген
бірліктермен v жылдамдығын, s кесіндісін және t уақытын өлшеуге болады.
Егер k коэффициентіне алдын ала бір белгілі мән берсек, онда 3-параграфта
айтылғандай, v, s және t физикалық шамаларының үшеуінің де өлшеу
бірліктерін түгелімен еркін сайлап алуға болмайды. Бұлардың тек екеуінің
ғана өлшеу бірліктерін еркін сайлап алуға болады, үшінші шаманың өлшеу
бірлігі (3) теңдікке лайық сайлап алынады, сонда k коэффициенті берілгенде
(3) теңдік сан жағынан орындалуға тиісті. Мысалы, k=1 деп ұйғарылса, (3)
формула мына түрде жазылады:
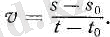(4)
Бұл формулада кездесетін шамалардың тек екеуінің ғана өлшеу бірліктерін
еркін сайлап алуға болады. Егер біз ұзындық бірлігі етіп сантиметрді (см),
уақыт бірлігі етіп секундты (сек) алсақ, сонда (4) формулаға лайық
жылдамдықтың бірлігі етіп 1 сек ішінде 1 см жол жүретін бір қалыпты
қозғалыстың жылдамдығын аламыз. Бұл CGS системасындағы жылдамдықтың бірлігі
болады, оны қысқаша смсек деп белгілейді. Бірліктердің басқа
системаларында жолдың бірлігі етіп метр (м) немесе километр (км) алынады,
ал уақыт бірлігі етіп секунд (сек) немесе сағат (сағ) алынады, сонда осыған
сәйкес жылдамдық бірліктері мсек және кмсағ болады. (4) формуладан:
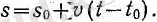(5)
Егер t0=0 және s0 = 0 болса, онда (5) формула мына түрде жазылады:
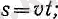(5а)
мұндағы s — дененің t уақыты ішінде жүрген жолы.
Біз (5а) формуланы (1) формуламен салыстыратын болсақ, дене бір қалыпты
қозғалған жағдайда оның жүрген жолы уақыттың сызықтық функциясы екендігін
көреміз.
Жолдың уақытқа сызықтық тәуелділігін графикпен көрсетуге болады.
Абсциссалар осінің бойына t уақытын, ординаталар осінің бойына s жолын
саламыз (2-сурет). Сонда (5а) формулаға сәйкес, 5 жолының t уақытына
тәуелділігін координаталар басынан өткен ОВ түзуі көрсетеді. Абсциссалар
осінде Ob кесіндісімен, кескінделген t уақыты аралығында дене s жолын
жүреді, ол жол Оа кесіндісімен немесе оған тең bВ кесіндісімен
кескінделеді.
2-суреттен мынаны табамыз:

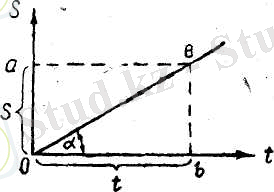
2-сурет. Бір қалыпты қозғалыс кезінде жүрілген s жолының t уақытына
тәуелділігі ОВ түзуімен кескінделеді.

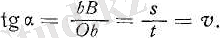(6)
Сонымен, біздің графигімізде v жылдамдығы α бұрышының тангенсі арқылы
кескінделеді; v жылдамдығы неғұрлым зор болса, ОВ түзуі мен t уақыттар
осінің арасындағы α бұрышы соғұрлым үлкен болады.

§ 6. Түзу сызықты айнымалы қозғалыс. Айнымалы қозғалыс кезінде бірдей
уақыт аралықтарында дененің жүрген жолдары бірдей болмайды. Мұндай жағдайда
қозғалыстың орташа жылдамдығы деген ұғым ендіруге болады. Айнымалы
қозғалыстың берілген t — t0 уақыты аралығындағы орташа жылдамдығы, дене бір
қалыпты қозғала отырып, айнымалы қозғалыс кезіндегідей, осы t — t0 уақыты
аралығында да s — s0 жолын жүре алатын бір қалыпты қозғалыстың жылдамдығына
тең. Сонымен, қозғалыстың орташа жылдамдығын v әрпімен белгілеп, былай
жазуға болады:

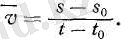
Орташа жылдамдықтың (v) мәні сол жылдамдық қарастырылып отырған уақыт
аралығына байланысты болады. Сондықтан орташа жылдамдық айнымалы
қозғалыстың жеткілікті сипаттамасы бола алмайды. Мысалы, поезд екі
станцияның арасында қозғалғанда бізге оның тек осы жолды тұтас жүргендегі
орташа жылдамдығы ғана емес, жолдың жеке участоктарындағы поездың
жылдамдығын да білу керек болуы мүмкін. Ол үшін біз жолды жеке ∆s
участоктарына бөліп, сол участоктарды жүруге кеткен ∆t уақыт аралықтарын
өлшеуіміз керек. Сонда:
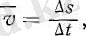(1)
бұл жолдың берілген ∆s участогындағы орташа жылдамдығы болып табылады.
Біз v орташа жылдамдығы анықталатын ∆t уақыт аралықтарын неғұрлым аз
етіп алсақ, қозғалыс сипаттамасын соғұрлым дәлірек анықтаймыз. Негізінде ∆t
уақыт аралығын өте аз етіп сайлап алып, сол уақыт аралығы ішіндегі
қозғалысты бір қалыпты деп санауға да болады. Сонда осы аз уақыт
аралығындағы орташа жылдамдық қозғалыстың жеткілікті сипаттамасы
болады; басқа сөзбен айтқанда, ол жолдың берілген нүктесіндегі v жылдамдығы
болып табылады.
Сонымен, айнымалы қозғалыстың жолдың берілген нүктесіндегі (немесе
берілген уақыт кезеңіндегі) жылдамдығы, жылдамдық анықталып отырған ∆t
уақыт аралығы шексіз кемігенде, орташа жылдамдық ұмтылатын шек болып
табылады.
Мұны математикаша былай жазады:
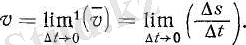(2)
Дифферендиалдық есептеуден 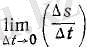жолдың уақыт бойынша алынған туындысы
екендігі мәлім; сонымен, жылдамдық сан жағынан жолдың уақыт бойынша алынған
туындысына тең:
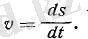(2а)
Осы айтылғанды график сызып түсіндіруге болады. Айнымалы қозғалыс
кезінде жүрілген жолдың уақытқа тәуелділігі, графикпен көрсеткенде, қисық
сызықпен кескінделеді.
Әр түрлі қозғалыстар үшін бұл қисықтың түрі әр түрлі болады; кейбір
дербес жағдайда ол 3-суретте көрсетілген ОАВ қисығына ұқсас болып келеді.

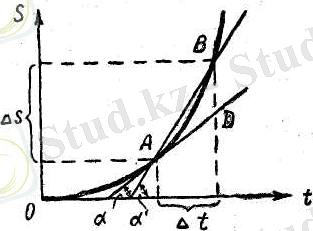
3-сурет. Айнымалы қозғалыстың жылдамдығы жанама мен Оt осінің
арасындағы α бұрышының тангенсі арқылы анықталады.

Суретке қарағанда ∆t уақыт аралығындағы v орташа жылдамдық мынаған тең:

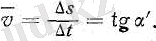
Біз v орташа жылдамдығын енгізе отырып, ∆t уақыт аралығындағы жолдың
уақытқа шын тәуелділігін көрсететін 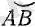доғасының орнына АВ хордасын
аламыз, яғни айнымалы қозғалыстың орнына бір қалыпты қозғалысты аламыз.
Жоғарыда айтылғандай, ∆t уақыт аралығын шексіз азайта отырып, берілген t
уақыт кезеңіндегі жылдамдықты табамыз; сонда шегіне жеткен АВ қиюшысы AD
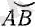жанамасына айналады да, АВ хордасы мен доғасы қосылып кетеді, яғни
шексіз аз ∆t уақыт аралығындағы айнымалы қозғалыс бір қалыпты қозғалыс
болып табылады. Сонымен:

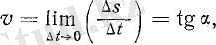
мұндағы α — Ot oci мен жолдың уақытқа тәуелділігін көрсететін қисықтың А
нүктесінен жүргізілген жанаманың жасаған бұрышы.
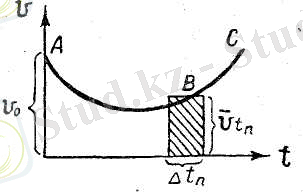
Айнымалы қозғалыс кезінде жүрілген жолдың жылдамдыққа тәуелділігін
қалай кескіндеуге болады, енді соны қарастырайық.
Абсциссалар осінің бойына t уақытын, ординаталар осінің бойына v
жылдамдығын салып график сызамыз. Сонда 4-суретте келтірілген ABC қисығы
бастапқы мәні vo-ге тең жылдамдықтың уақытқа байланысты өзгергенде
алғашқыда кеміп, кейін өсе бастағанын көрсетеді, бұл кейбір дербес жағдайда
кездеседі.
Қозғалысқа кеткен барлық t уақытты саны өте көп, өзі тым аз ∆t уақыт
аралықтарына бөлейік. Сонда (1) формула бойынша n-ші уақыт аралығында
жүрілген жол: 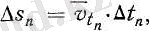мұндағы деп отырғанымыз ∆tn уақыт аралығындағы
орташа жылдамдық.

4-сурет. Шексіз аз ∆t уақыт аралығында жүрілетін жол штрихталған
бағанның ауданымен кескінделеді.

Графикпен көрсеткенде ол жол 4-суреттегі штрихталған жіңішке тік
төртбұрыштың ауданы арқылы кескінделеді. Барлық t уақыттың ішінде жүрілген
s жолы жеке ∆tn уақыт аралықтарында жүрілген барлық қысқа ∆sn жолдардын
қосындысына тең:
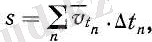(3)
яғни ОАВС фигурасын (5-сурет) бөлгенде шыққан барлық тік төртбұрыштардың
аудандарының қосындысына тең. Ең ақырында, шексіз аз ∆tn уақыт
аралықтарында тік төртбұрыштар да шексіз жіңішке болады да, олардың
аудандарынын қосындысы ОАВС фигурасының ауданымен беттеседі. Сонымен,
графикпен көрсеткенде барлық s жолы жылдамдықтың уақытқа тәуелділігін
көрсететін АВ қисығы мен сол жолды жүруге кеткен t уақыттық басы мен
ақырына сәйкес келетін ординаталардың арасындағы ауданмен кескінделеді.

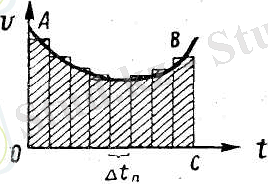
5-сурет. Шектелген t уақыт аралығында жүрілетін жол ОАВС фигурасының
ауданымен кескінделеді.

§7. Тузу сызықты бір қалыпты айнымалы қозғалыс. Үдеу. Бір қалыпты
айнымалы, қозғалыс деп, еркін алынған өз ара тең ∆t уақыт аралықтарында v
жылдамдығы бірдей ∆v шамаға өзгеріп отыратын қозғалысты айтады. Бұл
жағдайда, егер ∆v-нің таңбасы жылдамдықтың таңбасымен бірдей болса, яғни
уақытқа байланысты жылдамдықтың сан мәні артып отырса, ондай қозғалыс бір
қалыпты үдемелі қозғалыс деп аталады; егер ∆v-нің таңбасы жылдамдық
таңбасына кері болса, яғни уақытқа байланысты жылдамдықтың сан мәні кеміп
отырса, ондай козғалыс бірқалыпты баяу қозғалыс деп аталады.
Уақытқа байланысты жылдамдық қаншалықты тез өзгеретіндігін сипаттау
үшін үдеу деп аталатын физикалық шама енгізіледі. Түзу сызықты бір қалыпты
айнымалы қозғалыстың үдеуі (w) дегеніміз — физикалық шама, ол жылдамдықтың
өсімшесіне тура пропорционал және осы өсімше пайда болған уақыт аралығына
кері пропорционал болады.
Мысалы, t0 уақыт кезеңіндеп жылдамдықтың мәні v0, ал t уақыт
кезеңіндегі жылдамдықтың мәні v болсын, сонда t — t0 уақыты ішінде
жылдамдық v — v0-ға өзгереді де, математикаша үдеу (w) былай жазылады:
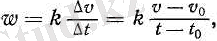(1)
мұндағы k — пропорционалдық коэффициент, оның мәні v жылдамдығы мен t
уақытының өлшеу бірліктерін сайлап алуға байланысты. Бір қалыпты айнымалы
қозғалыстың үдеуі тұрақты шама болады. Егер пропорционалдық коэффициентті
k= 1 деп ұйғарсақ, онда үдеу
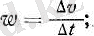(1а)
сонда CGS системасында үдеу бірлігі ретінде әрбір секунд сайын жылдамдығы 1
смсек-ке өзгеріп отыратын қозғалыстың үдеуі алынуға тиіс; үдеудің осы
бірлігі қысқаша 1 смсек2 деп белгіленеді. Бірліктердің MKS системасында
үдеудің, бірлігі ретінде әрбір секунд сайын жылдамдығы 1 мсек-ке өзгеріп
отыратын қозғалыстың үдеуі алынады (қысқаша 1 мсек2).
Егер коэффициент k=1 болса, онда (1) формуладан мынау шығады:
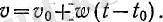(2)
Сонымен, бір қалыпты айнымалы қозғалыс кезінде жылдамдық уақытқа
байланысты өзгереді. Егер t0 = 0 болса, онда (2) теңдік бойынша:
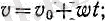(2а)
егер бастапқы жылдамдық v0 = 0 болса, онда
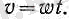(2б)
Жылдамдықтың ∆v өсімшесінің таңбасы қандай болса, w үдеуінің де таңбасы
сондай болады, сондықтан бip қалыпты үдемелі қозғалыстың үдеуі (w) оң шам,
ал бір қалыпты баяу қозғалыстың үдеуі (w) теріс шама болады.
Бір қалыпты айнымалы қозғалыста жүрілетін жолды анықтайық. Жеңіл болу
үшін бастапқы жылдамдық v0 = 0 деп ұйғарайық; сонда (26) формула бойынша
жылдамдықтың уақытқа графиктік тәуелділігі (w0 десек) ОА түзуімен
кескінделеді (6-сурет). Солай болғанда, бұдан бұрынғы параграфта айтылған
бойынша t уақыты ішінде жүрілген s жолы ОАВ фигурасының ауданымен
кескінделеді. Біз қарастырып отырған жағдайдағы фигура үшбұрыш
болғандықтан, оның ауданы мынаған тең:

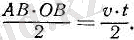
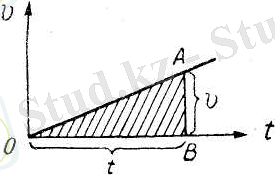
6-сурет. Бір қалыпты қозғалыс кезінде жүрілген жол ОАВ үшбұрышының
ауданымен кескінделеді.

Сонымен, t уақыты ішінде жүрілген s жолы мынадай болады:
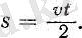(3)
Мұндағы v жылдамдығының орнына оның (26) формулада w үдеуі мен t уақыты
арқылы табылған мәнін қойсақ, онда мынау шығады:
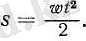(4)
Егер бастапқы кезде жылдамдық нольге тең болмай, оның мәні v0 болса,
онда
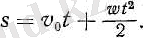(4а)
Денелердің Жер бетінде еркін түсуі бір қалыпты айнымалы қозғалысқа
мысал бола алады. Бұл жағдайда үдеу мынаған тең:

Ауадағы денелердің төмен түсуін тек ауаның кедергісінің ролі аз
болғанда ғана бір қалыпты айнымалы қозғалыс деп санауға болады (мысалы,
шамалы биіктіктен тастың түсуі); ауа кедергісінің ролі үлкен болған кезде,
ауадағы дененің төмен түсуі бір қалыпты қозғалысқа жатады (16-параграфты
қараңдар); мысалы, судың тұманға айналған ұсақ тамшылары ауада бір қалыпты
төмен қарай қозғалады; парашютін жайған парашютист те ауада төмен қарай бір
қалыпты қозғалады.
Бір қалыпты айнымалы қозғалысқа бірнеше мысал келтірейік.
1-мысал. Биіктігі 20 м мұнараның төбесінен тас түсірілген, оның
бастапқы жылдамдығы нольге тең. Ауаның кедергісін елемей мыналарды
анықтайық: тастың түсуіне қанша уақыт кетеді? Ол Жерге қандай жылдамдықпен
келіп жетеді?
Шешуі. Есептің шарты бойынша тастың қозғалысын бір қалыпты айнымалы деп
санауға болады, сондықтан осы параграфта келтірілген формулаларды
пайдалануға да болады.
(4) формуладан тастың төмен түсуіне кеткен уақытты табамыз:
(5)
мұндағы s — тастың жүрген жолы, яғни тас түсірілген мұнараның биіктігі;
үдеудің мәні сонда

Қозғалыстың ақырындағы жылдамдық:

Жүрілген s жолының аяғындағы v жылдамдығын s жолы мен w үдеуі арқылы
алгебраша өрнектеуге де болады. Ол үшін мына v = wt формуласындағы t-нің
орнына, оның (5) теңдікте келтірілген мәнін жазамыз, сонда

бұдан
(6)
2-мысал. Тік жоғары лақтырылған тас 30 м биіктікке көтерілді. Ол осы
биіктікке қанша уақытта көтеріледі және қанша уақыттан кейін қайтадан Жерге
келіп түседі? Оньщ бастапқы жылдамдығы қандай болу керек?
Шешуі. Тік жоғары лақтырылған тастың қозғалысы, тас жоғары көтеріліп
бара жатқанда, бір қалыпты баяу қозғалыс болады. Сондықтан оның үдеуі w =
-g, ал көтерілген биіктігі
(7)
болады, мұндағы v0 — тастың бастапқы жылдамдығы, t — тас жоғары көтерілуге
кеткен уақыт. Ең жоғарғы нүктедегі жылдамдық vs нольге тең болатындықтан,
бастапқы v0 жылдамдығын былай табамыз:

бұдан
(8)
сонда (7) формула бойынша

Бұдан тас s биіктікке көтерілуге кететін уақыт мынаған тең болады:

Осы табылған уақытты (5) теңдік бойынша аныкталған уақытпен салыстырып
қарасақ, тас s биіктікке көтерілуге кететін уақыт, ол s биіктіктен тастың
еркін түсуіне керек болатын уақытка тең екендігін көреміз. Табылған t-нің
мәнін (8) теңдіктегі орнына қойсақ, мына формула шығады:

Сөйтіп, тік жоғары лақтырылғандағы тастың жылдамдығы, оның сол s
биіктіктен еркін түскендегі жылдамдығына тең [(6) формуланы қараңыз].
Шамалардың берілген сан мәндерімен пайдаланып және дәлелдеп шығарылған
теңдіктер бойынша v0 мен t-нің мәндерін табамыз:

§8. Кез келген түзу сызықты қозғалыстың үдеуі. Түзу сызықты айнымалы
қозғалысты жалпы алып қарастырғанда орташа үдtу деген ұғым енгізуге болады.
Дененің берілген ∆t уақыт аралығындағы орташа w үдеуі деп бір қалыпты
айнымалы қозғалыстың үдеуіне тең үдеуді айтады, сонда бір қалыпты үдей
қозғалған дененің сол ∆t уақыт аралығындағы жылдамдығының ∆v өсімшесі
қарастырылып отырған дененікіндей болуы керек. Сөйтіп:
(1)
Берілген уақыт кезеңіндегі жылдамдық туралы ұғым қалай енгізілсе,
берілген уақыт кезеңіндегі үдеу туралы ұғым да дәл солай енгізіледі. Біз ∆t
уақыт аралығын соншалықты азайталық, сонда осы уақыт аралығында қозғалысты
іс жүзінде бір қалыпты айнымалы қозғалыс деп есептеуге боларлықтай болсын.
Сондай уақыт аралығындағы орташа үдеу , уақыт кезеңіндегі үдеу болып
табылады. Сонымен берілген уақыт кезеңіндегі үдеу деп, орташа үдеуі алынып
отырған ∆t уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын
шегін айтады, яғни
(2)
мұндағы ∆v — жылдамдықтың шексіз аз ∆t уақыт аралығындағы шексіз аз
өзгерісі.
Дифференциалдық есептеуден мынаны білеміз:
(2а)
яғни, үдеу, сан жағынан алғанда, жылдамдықтың уақыт бойынша алынған
туындысына тең. Ал болғандықтан,
(26)
яғни удеу, сан жағынан алғанда, жолдың уақыт бойынша алынған екінші
туындысына тең.
Бұл қатынастарды да, жылдамдықты қарастырғандай, графикпен түсіндіруге
болады. 7-суреттегі ОАВ қисығы жылдамдықтың уақытқа тәуелділігін көрсетеді
дейік. Сонда, t-ден t+∆t-ге дейінгі уақыт аралығындағы орташа үдеу w
мынаған тең болады:

мұндағы β1 — Ot осі мен АВ қиюшының арасындағы бұрыш. Біз уақыт аралығын
шексіз азайта берсек, сонда АВ қиюшысы AC жанамасына ұмтылады да, ең
ақырында мынау шығады:

мұндағы β — Ot осі мен жылдамдықтың уақытқа тәуелділігін кескіндейтін
қисықтың А нүктесінен жүргізілген AC жанамасының арасындағы бұрыш.

7-сурет. Айнымалы қозғалыстың үдеуі жанама мен Ot осінің арасындағы β
бұрышыньщ тангенсі арқылы анықталады.

§9. Жылдамдық және үдеу — векторлар. Жылдамдық тек сан мәнімен ғана
емес, сонымен қатар бағытымен де сипатталады. Дененің қозғалысын сипаттау
үшін тек оның жылдамдығының сан мәнін ғана көрсетіп қою жеткіліксіз, оған
қосымша ол қай бағытпен қозғалып бара жатқанын да көрсету қажет.
Өзінің тек сан мәнімен ғана емес, сонымен қатар, бағытымен де
сипатталатын шамалар векторлар деп аталады. Кейбір шамаларды анықтау үшін
олардың тек сан мәнін білу жеткілікті, ондай шамалар (мысалы, уақыт
аралығы, масса, тығыздық т. с. с.) скалярлар деп аталады.

8-сурет. А және В векторларын қосқанда шығатын С қорытқы векторы сол A
және В векторлары қабырғалары болып келетін параллелограмның диагоналымен
кескінделеді.

Векторды стрелкамен кескіндеуге болады, сонда оның еркін алынған
бірлікпен өлшенген ұзындығы вектордың сан мәніне тең болады да, бағыты
вектордың бағытымен дәл келеді. Векторларды қарайтылған әріптермен, олардың
сан мәнін кәдімгіше жазылған сол әріптердің өзімен белгілеуге келісілген;
мысалы, А әрпі векторды, ал А әрпі вектордың сан мәнін көрсетеді. Вектордың
алдындағы минустың мәні, — А векторы өзімен ұзындығы бірдей А векторына
қарама-қарсы бағытталғандығын көрсетеді.
Тәжірибеге қарағанда вектор болып табылатын физикалық шамаларды қосу
алгебралық шамаларды қосудан өзгеше. Векторларды қосудың тәсілі
параллелограмм ережесі бойынша анықталады: А және В векторларын қосқанда
шығатын қорытқы С векторы А және В векторлары қабырғалары болып келген
параллелограмның диагоналымен кескінделеді (8-сурет).
Саны екіден көп векторларды қосқанда шығатын қорытқы векторды
параллелограмм ережесін біртіндеп қолдана отырып табуға болады. Егер біз
сынық сызық сызсақ, онын, құраушылары шамасы мен бағыты жағынан қосылғыш A,
B, С, D векторларымен дәл келсе, сонда шыққан нәтиже де жоғарыда
айтылғандай болады (9-сурет). Сонда қорытқы Ғ векторы сынық сызықтың бір
ұшынан екінші ұшына жүргізілген тұйықтаушымен кескінделеді.
А және В векторларының айырмасын В' = -В векторын енгізу арқылы табуға
болады:
А – В = А+ В' (1)
Сан жағынан В векторына тең, бірақ қарама-қарсы бағытталған В' векторын
салып, А және В' векторларының қосындысы болатын С векторын табамыз.
Сонымен қатар (1) теңдік бойынша С векторы А және В векторларының айырмасы
да болады.
Векторды анықтау үшін оның не тікелей шамасы мен бағыты көрсетіліп
немесе оның координаталар осьтеріне түсірілген проекциялары беріледі. Егер
есеп жазық болып, тік бұрышты координаталар системасын пайдаланған болсақ
(10-сурет), онда A векторы өзінің координата осьтеріне түсірілген Ах және
Ау проекциялары арқылы анықталады. Сонда 10-сурет бойынша мынаны табамыз:

(2)

9-сурет. А, В, С, D векторларының қосындысы болып табылатын Ғ векторы
сынық сызықтың тұйықтаушысымен кескінделеді, сонда A, B, C, D векторлары
оның құраушылары болады.

А векторының бағыты не α бұрышымен, немесе β бұрышымен анықталады;
сонда α бұрышы осы вектор мен ОХ осінің арасындағы бұрыш, β бұрышы сол
вектор мен ОУ осінің арасындағы бұрыш болады. 10-суреттен
(3)
болатынын көреміз.

10-сурет. Ах және Ау кесінділері А векторының ОХ және ОУ осьтеріне
түсірілген проекциялары болып табылады.

Түзу сызықты қозғалыстың жылдамдығы — вектор, ол дене қозғалатын
түзудің бойымен, сол дененің қозғалатын жағына қарай бағытталған.
Жылдамдықты вектор деп түсіну дұрыс болып шықты, себебі жылдамдықтарды
қосудың векторлық ережесіне сүйеніп қозғалыстарды есептегенде шыққан
нәтижелер нақты қозғалыстарды бақылағанда, табылған нәтижелерге сай келеді.
Егер дене бір мезгілде бір қалыпты түзу сызықты екі қозғалысқа ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.