Жалпы бірінші шеттік есептер мен стационарлық біртекті емес мәселелер: айнымалыларды ажыратудың жалпы схемасы, меншікті мәндер және Фурье жіктелуі


Лекция 5. Жалпы бірінші шеттік есеп және айннымалыларды ажыратудың жалпы схемасы.
1. Жалпы бірінші шеттік есеп және стационар біртекті емес есептер.
2. Бастапқы шартсыз есептер.
3. Шоғырланған күш.
4. Жалпы схема.
1 . Тербеліс туңдеуінің жалпы бірінші шеттік есебін қаралық:
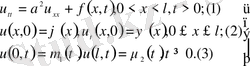
Белгісіз
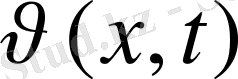 функциясымен, U(x, t) - белгілі деп, шешім u(x, t) құрылады:
функциясымен, U(x, t) - белгілі деп, шешім u(x, t) құрылады:
u(x, t) =U(xt) +
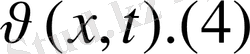
Онда
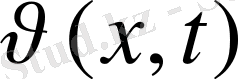 келесі есептің шешімі деп іздестіріледі:
келесі есептің шешімі деп іздестіріледі:
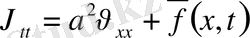 ,
,
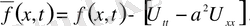
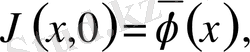
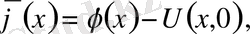
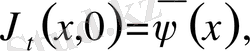
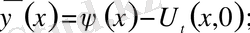
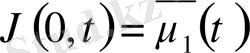
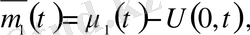
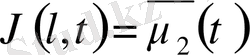
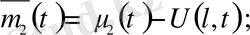
U(x, t) функциясын
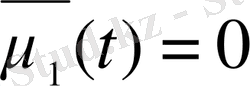 және
және
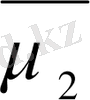 (t) =0 болатындай етіп аламыз, яғни
(t) =0 болатындай етіп аламыз, яғни
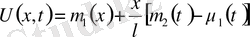
Сонымен u(x, t) үшін жалпы бірінші шеттік есеп, бұған дейін қарастырылған шекаралық шарттары нөл болатын,
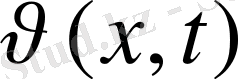 үшін жалпы есепке келтірілді, онда
үшін жалпы есепке келтірілді, онда
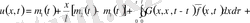
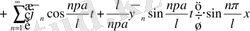 (5)
(5)
Стационар біртекті емес шеттік есептерді қарастырайық
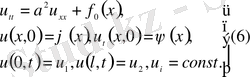
Шешім u(x, t) =
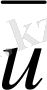 (x, t) +
(x, t) +
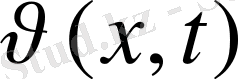 түрінде іздестіріледі,
түрінде іздестіріледі,
 (x) келесі шарттардан анықталады
(x) келесі шарттардан анықталады
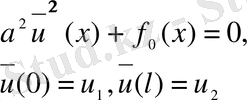 онда
онда
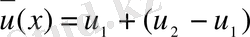
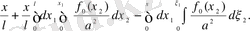
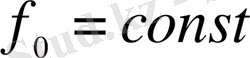 десек, онда
десек, онда
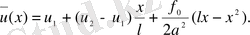
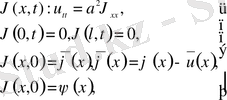
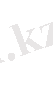
Мысал.
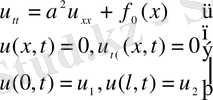 Бұл есепте
Бұл есепте
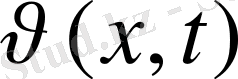 үшін келесі есеп алынады:
үшін келесі есеп алынады:

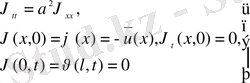
2. Практикада бастапқы шартсыз есептер де жиі кездеседі
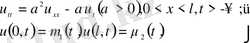
U(l, t) =Acoswt (немесе u(l, t) =Bsinwt), u(0, t) =0 болғанда u(l, t) =Ae
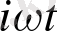 түрінде қарастыру тиімді.
түрінде қарастыру тиімді.
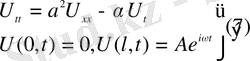 есебінің шешімін табайық.
есебінің шешімін табайық.
U(x, t) =X(x) e
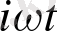 десек:
десек:
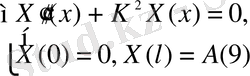
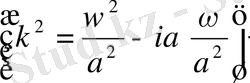 (8)
(8)
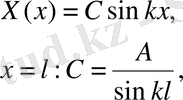
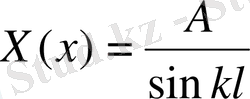
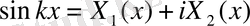 (10)
(10)
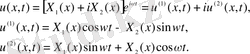
3
.
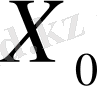 нүктесінде f(t) шоғырланған күш әсері бар жағдайды қарастырайық, онда
нүктесінде f(t) шоғырланған күш әсері бар жағдайды қарастырайық, онда
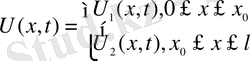
Есеп:
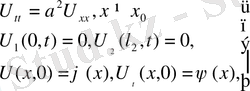 (6)
(6)
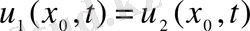 ,
,
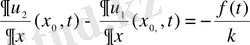 (7) -түйіндестік шарты.
(7) -түйіндестік шарты.
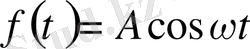 ,
,
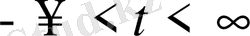 десек, шешім мына түрде іздестіріледі.
десек, шешім мына түрде іздестіріледі.
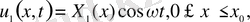 (8)
(8)
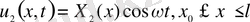
Онда:
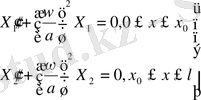 (9)
(9)
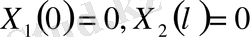 (10)
(10)
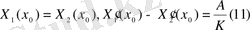
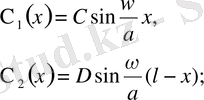
(7) -шарттан:
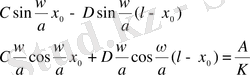
Сонымен
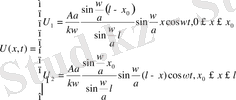 (12)
(12)
Дәл осылайша
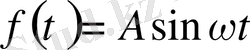 жағдайы шешімі де құрылады. Егер f(t) =
жағдайы шешімі де құрылады. Егер f(t) =
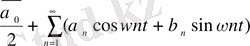 болса, онда шешім:
болса, онда шешім:
 (13)
(13)
4.
Біртекті емес ішек тербелісінің есептеріне де айнымалыларды ажырату әдісі қолданылатынын корсетелік: Теңдеудің L
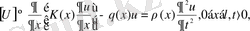 (14)
(14)
Берілген шарттарды
u= (0, t), u(l, t) =0, t
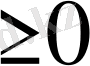 , (15)
, (15)
u(x, 0) =0,
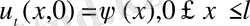 (16)
(16)
орындайтын шешімін табу керек.
Мұндағы k, q,
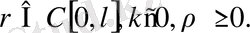
Алдымен (14) теңдеудің (15) шарттарымен шешімі
u(x, t) =X(x) T(t) түрінде ізделінеді.
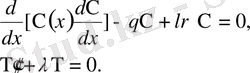
Онда X(x) үшін меншікті мәндер шеттік есебін аламыз:есептің нөлден өзге шешімдері бар болатын
 параметірінің мәндерін және осы шешімдерін табу керек.
параметірінің мәндерін және осы шешімдерін табу керек.
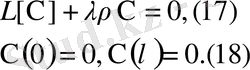
Параметр
 ның мұндай мәндері меншікті мәндер, ал оларға тиісті нөл емес шешімдері (17) -(18) есебінің меншікті функциялары деп аталады.
ның мұндай мәндері меншікті мәндер, ал оларға тиісті нөл емес шешімдері (17) -(18) есебінің меншікті функциялары деп аталады.
Меншікті мәндер (мм) және оларға тиісті меншікті функциялардың (мф) негізгі қасиеттеріне тоқталайық.
1) Саналымды жиын құрайтын
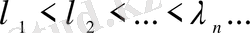 -меншікті мәндер және меншікті функциялар
-меншікті мәндер және меншікті функциялар
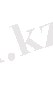
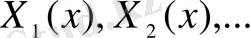 бар.
бар.
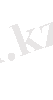
2 )
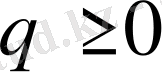 болса барлық
болса барлық

3)
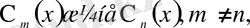 аралықта
аралықта

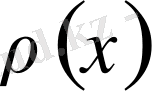 -салмағымен ортогоналды:
-салмағымен ортогоналды:
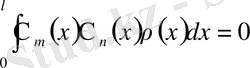
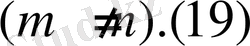
4) (В. А. Стеклов теоремасы )
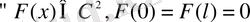 болса, м ф-р
болса, м ф-р
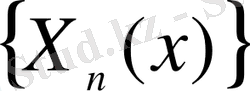 қатарына, бірқалыпты және абсолютті жинақы, жіктеледі:
қатарына, бірқалыпты және абсолютті жинақы, жіктеледі:
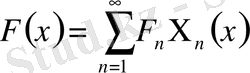 ,
,
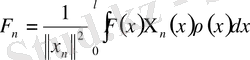 , (20)
, (20)
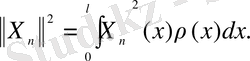
2), 3) қасиеттерді дәлелдеуде Грин формуласы қолданылады:
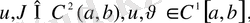
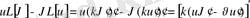 ,
,
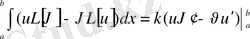
 (21) Грин формуласы.
(21) Грин формуласы.
Енді бастапқы есепке (14) -(16) оралсақ,
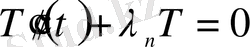 (22)
(22)
теңдеуінен
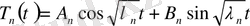 ,
,
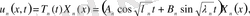
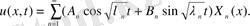 (23)
(23)
Бастапқы шарттардан:
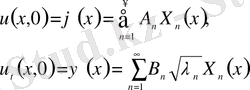
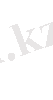

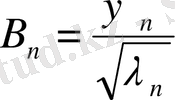 (24)
(24)
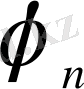 және
және
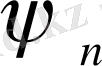 тиісінше
тиісінше
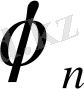 және
және
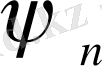 функцияларын
функцияларын
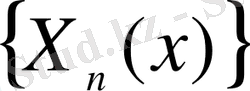 жүйесінде
жүйесінде
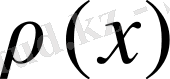 салмағымен Фурье қатарына (20) жіктеу коэффиценттері.
салмағымен Фурье қатарына (20) жіктеу коэффиценттері.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz