Нюрнберг қайшысы типті төменгі жетекті жүк көтергіш механизмдердің күштік талдауы және гидроцилиндрлік жетек тізбегін оңтайландыру


2 “НЮРНБЕРГ ҚАЙШЫСЫ” ТИПТІ ТӨМЕНГІ ЖЕТЕКТІ ЖҮК КӨТЕРГІШ МЕХАНИЗМДЕР ЖЕТЕГІН ОПТИМАЛДАУ
2. 1 Төменгі жетекті сұлбаның күштік анализі
, а - суретте 7 платформасы бар жүк көтеруші механизмнің кинематикалық сұлбасы және 1 кіріс буыны көрсетілген. “Нюрнберг қайшысы” атты дәстүрлі механизмді төменгі жетекті сұлбасы атау қабылданған, сызықтық қозғалыстың С сырғаның жалпыланған координатасы q=s; s=AС бар. Механизмнің кинематикалық сұлбасы буындар ұзындығымен AF=FJ=CD=2c және платформаның көтерлу биіктігімен h=AJ анықталады .
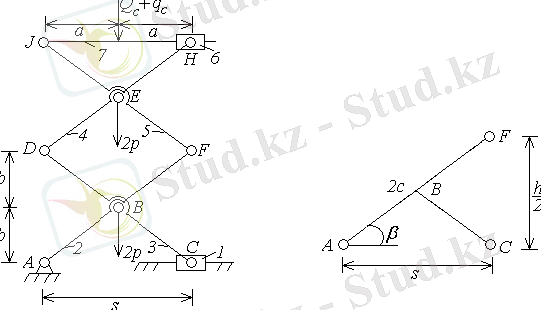
а ) б )
1-сурет
Механизм кинематикасы өте қарапайым формулалармен анықталады.
Тікбұрышты
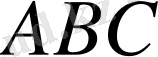 үшбұрышынан ( 1,
б
-сурет)
үшбұрышынан ( 1,
б
-сурет)
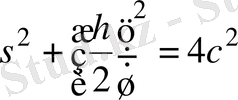 (1)
(1)
Бұл өрнекті дифференциялдасақ
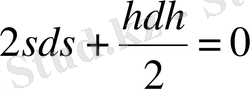 ,
,
Ендеше
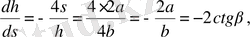
Мұндағы
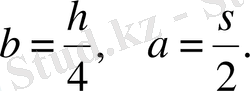
Айталық, Q және q с - сәйкесінше жүк және платформаның өз салмағы болсын. Ал p - бір сырықтың салмағы. Онда теңгеріуші күш мына формуламен анықталады:
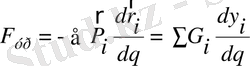 , (2)
, (2)
Мұндағы
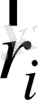 - сыртқы күштердің әсер ету нүктелерінің радиусы -векторы,
- сыртқы күштердің әсер ету нүктелерінің радиусы -векторы,
 - механизмге әсер ететін сыртқы күштер ретінде ауырлық күштерін ғана қарастырамыз:
- механизмге әсер ететін сыртқы күштер ретінде ауырлық күштерін ғана қарастырамыз:
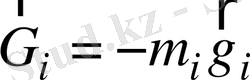 .
.
Осыны есепке ала отырып
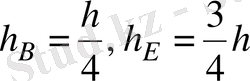 , теңгеруші күш былай анықталады.
, теңгеруші күш былай анықталады.
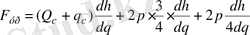 ,
,
яғни
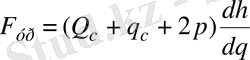 . (3)
. (3)
Бұған
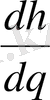 мәнін қойып, аяғында керек өрнекті аламыз:
мәнін қойып, аяғында керек өрнекті аламыз:
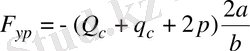 аламыз (4)
аламыз (4)
Енді топсалардағы реакцияларды анықтайық ( 2-сурет) .
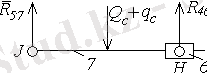
2-сурет
6-7 Ассура тобына әсер ететін реакцияларды анықтау үшін
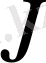 және
және
 нүктелеріне сәйкес 6-7 буындардың моменттер теңдеуін жазайық.
нүктелеріне сәйкес 6-7 буындардың моменттер теңдеуін жазайық.
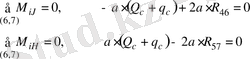 (5)
(5)
Бұдан шығатыны
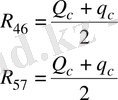 . (6)
. (6)
Енді екі сырықты 4-5 топты қарастырайық. 4 және 5 буындардағы
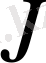 және
және
 топсаларына
топсаларына
 и
и
 , вертикал төмен бағытталған және мәндері
, вертикал төмен бағытталған және мәндері
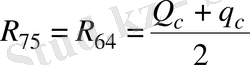 рекциялар әсер етеді. Онда
А
және
В
топсаларының вертикал құраушылары (
рекциялар әсер етеді. Онда
А
және
В
топсаларының вертикал құраушылары (
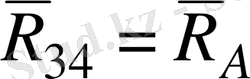 и
и
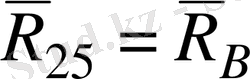 )
)
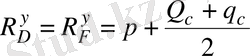 . (7)
. (7)
А горизонталь құраушылары С нүктесі бойынша 4 сырыққа әсер ететін күштер моменттерінің қосындысының теңдеуін 0 -ге теңестіру арқылы табамыз:
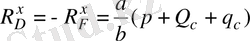 (8)
(8)
4 сырықтағы күштер тепе-теңдігінің шартынан табамыз:
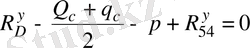 , (9)
, (9)
Бұдан:
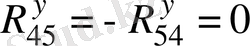 . (10)
. (10)
2-3 Ассура топы үшін де ұқсас есептеулер жүргізіп (3, в-сурет),
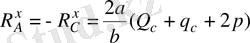 (11)
(11)
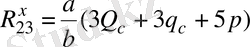 (12)
(12)
болғанын табамыз

а ) б )
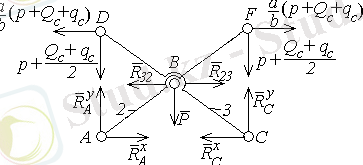
в )
3-сурет
Енді келесі сан мәндерін қойайық:
-жүк массасы (пайдалы жүктеме) :
кг (жүк салмағы
Н) ;
- платформа массасы:
кг (жүк көтеруші платформының салмағы
) ;
-бір сырықтың массасы:
кг (сырықтың салмағы
) ;
-сырықтың ұзындығы
м.
Онда механизмнің төменгі күйінде (ерекше күйге жақын кезде) :
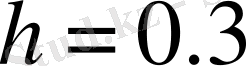 м,
м,
 м,
м,
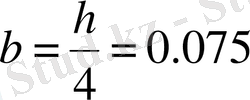 м, теңгеруші күштің мәнін аламыз-
м, теңгеруші күштің мәнін аламыз-
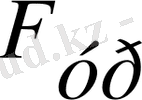 = 47. 024 кН, яғги 4798 кгС. Барлық нәтижелер 1-кестеге енгізілген.
= 47. 024 кН, яғги 4798 кгС. Барлық нәтижелер 1-кестеге енгізілген.
Ал жоғары күйде, мұндағы
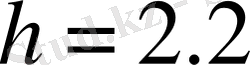 м,
м,
 м,
м,
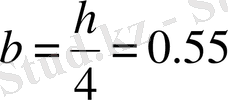 м, теңгеруші күш -
м, теңгеруші күш -
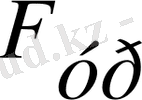 = 3. 068 кН, яғни. 313 кгС .
= 3. 068 кН, яғни. 313 кгС .
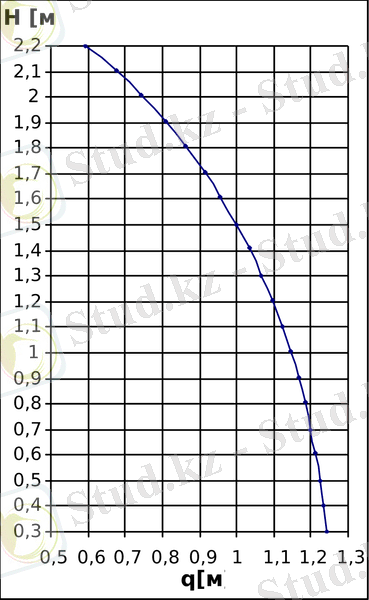
4,
а-
суретте
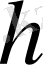 =0, 3м -ден 2, 2м-ге дейінгі өзгеріс кезіндегі платформаның көтерілу биіктігіне жалпылама координаттың
=0, 3м -ден 2, 2м-ге дейінгі өзгеріс кезіндегі платформаның көтерілу биіктігіне жалпылама координаттың
 тәуелділік графигі көрсетілген.
тәуелділік графигі көрсетілген.
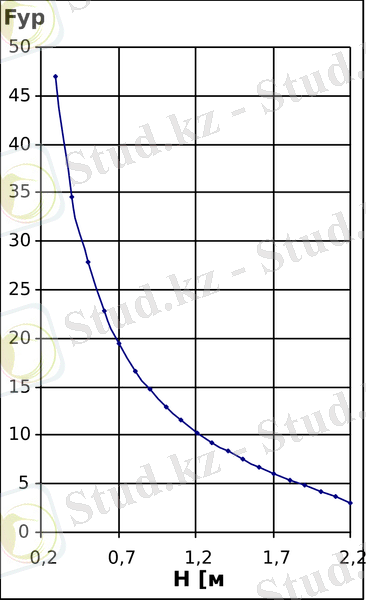
Ал 4, б -суретте теңгеруші күштің платформаның көтерілу биіктігіне тәуелділік графигі көрсетілген.
 (
а
) и
(
а
) и
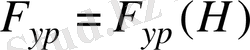 (
б
) тәуелділіктерінің графиіктері.
(
б
) тәуелділіктерінің графиіктері.
1-кесте
(3) формула бойынша
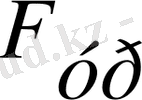 шамасы
шамасы
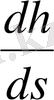 өзгерісіне тәуелді, ол
өзгерісіне тәуелді, ол
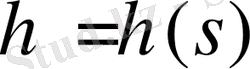 графигіне жанама бұрышының тангенсіне тең. Төменгі күйде
графигіне жанама бұрышының тангенсіне тең. Төменгі күйде
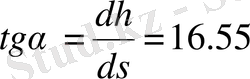 . Онда керек жүкті механизм сырықтарымен бірге көтеру үшін пайдалы жүктемеге қарағанда 16. 55 есе көп күш қажет. Бұл қарастырылып отырған механизмдегі күштің берілуі тиімділктен өте алыс жатқандығын білдіреді. Сәйкесінше топса реакциялардыңда төменгі күйде (ерекше күйге аса жақын
. Онда керек жүкті механизм сырықтарымен бірге көтеру үшін пайдалы жүктемеге қарағанда 16. 55 есе көп күш қажет. Бұл қарастырылып отырған механизмдегі күштің берілуі тиімділктен өте алыс жатқандығын білдіреді. Сәйкесінше топса реакциялардыңда төменгі күйде (ерекше күйге аса жақын
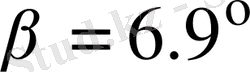 ) сан мәндері аса жоғары. Бұл массасы 150кг жүкті көтеру үшін 4798 кгС тан аз емес күш қажет деген сөз. Ал топсалардағы және 2 сырықтағы (кинематикалық жұптардағы) үйкеліс күштерін жеңу үшін одан да көп күш қажет болады.
) сан мәндері аса жоғары. Бұл массасы 150кг жүкті көтеру үшін 4798 кгС тан аз емес күш қажет деген сөз. Ал топсалардағы және 2 сырықтағы (кинематикалық жұптардағы) үйкеліс күштерін жеңу үшін одан да көп күш қажет болады.
2. 2 Тербелмелі гидроцилиндрлі сұлбаның күштік анализі
Қазіргі кезде өндірісте көп қолданылатын "Нюрнберг қайшылары" конструкцияларында платформаның қозғалмалы буындарды гидроцилиндр мен байланыстыратын жетек сұлбасы қолданылады ( 5-сурет) .
6,
а-
суреттегі жетек сұлбасын қарастырайық, мұнда
8
-
9
гидроцилиндр 3 және 4 буындарын байланыстырып тұр (кіріс кинематикалық тізбек
 ) .
) .
а ) б )
6-сурет
6, б -суреттерде көрініп тұрғандай, қозғалмалы сырықтардың салыстырмалы қозғалысы берілген (ҚССБҚ), механизмдер түріне жатқызуға болады. Біздің жағдайда 8 және 9 буындар. Сондықтан олардың күштік анализінің реті әдеттегідей емес, Ассур тобының қабатталу ретыне кері бағтталған. [Джо, Ибр, Озол, Кожевн] рет бойынша тізбектей анализделінеді. Мұндай механизмдерді Ассур тобына бөліп алуға болмайды. Осындай механизмдердің күштік анализдеу нұсқаларын пайдалана отырып([Ибр] жұмысында ұсынылған), анализді келесі ретпен жүргіземіз.
Алдыңғы жағдайдағы сияқты,
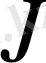 және
және
 шарнирлердегі реакция:
шарнирлердегі реакция:
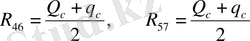 (13)
(13)
Ары қарай
 және
және
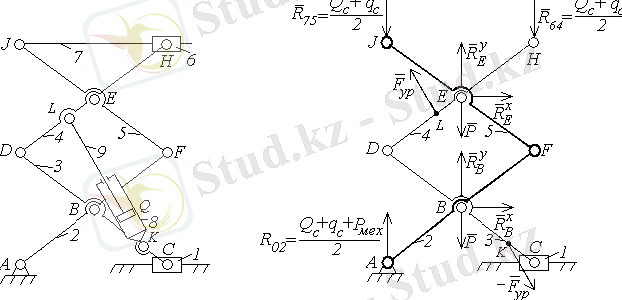
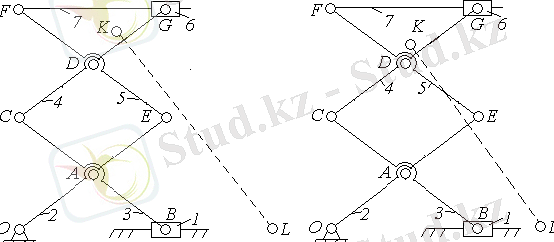
 топсаларына тірек жағынан әсер ететін реакцияларды анықтайық. Ол үшін Ассурдың II кластық - УГА(
1
-У(
2, 3, 4, 5, 6, 7
) ) ( 7-сурет) тобынан тұратын шартты механизмді есептейміз, мұндағы У - шартты буын, 8-9 сырықтар қозғалысы фиксацияланған
2-3-4-5-6-7
сырықтарынан құралған.
топсаларына тірек жағынан әсер ететін реакцияларды анықтайық. Ол үшін Ассурдың II кластық - УГА(
1
-У(
2, 3, 4, 5, 6, 7
) ) ( 7-сурет) тобынан тұратын шартты механизмді есептейміз, мұндағы У - шартты буын, 8-9 сырықтар қозғалысы фиксацияланған
2-3-4-5-6-7
сырықтарынан құралған.
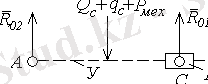
7-сурет
2-3-4-5-6-7
сырықтар тобы үшін
 және
және
 нүктелері бойынша моменттер теңдеуін жазайық (шартты буынды құраушылар) .
нүктелері бойынша моменттер теңдеуін жазайық (шартты буынды құраушылар) .
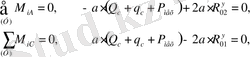 (14)
(14)
мұндағы
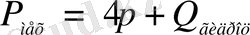 механизімнің
механизімнің
 жүк және
жүк және
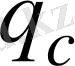 платформа салмағынсыз «таза» өз салмағы.
платформа салмағынсыз «таза» өз салмағы.
Іздеп отырған мәндерді анықтаймыз
 (15)
(15)
Ары қарай
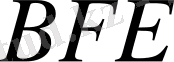 кинематикалық тізбегін қарастырайық (
2
-
5
сырықтар), соның ішінде
кинематикалық тізбегін қарастырайық (
2
-
5
сырықтар), соның ішінде
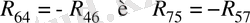 . В нүктесі бойынша
2
-
5
сырықтардың моменттер теңдеуін қолдана отырып
. В нүктесі бойынша
2
-
5
сырықтардың моменттер теңдеуін қолдана отырып
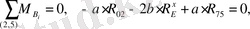 (16)
(16)
бұдан
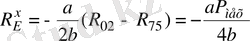 Equation. 3 . (17)
Equation. 3 . (17)
ОХ өсі бойынша күштердің тепе-теңдік теңдеуінен
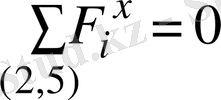
, онда
.
5 сырық үшін
 нүктесі бойынша моменттер теңдеуін жазайық:
нүктесі бойынша моменттер теңдеуін жазайық:
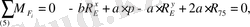 (18)
(18)
бұдан
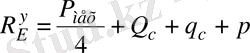 .
.
2-5 жүйесі үшін
ОY ө
сі бойынша күштердің тепе-теңдік теңдеуінен
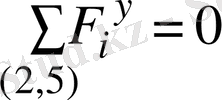
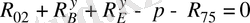 (19)
(19)
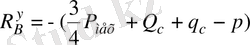 .
.
Күштердің тепе-теңдік теңдеуінен жеке 5 сырық үшін
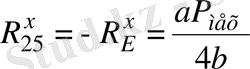 . (20)
. (20)
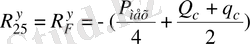 . (21)
. (21)
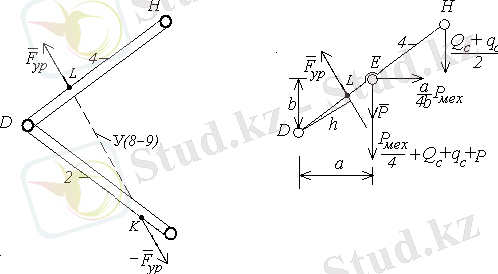
Енді теңгеруші күшті анықтаймыз, ол 4 сырықтың
 кинематикалық жұбына түсірілген ( 8-сурет)
кинематикалық жұбына түсірілген ( 8-сурет)
а ) б )
8-сурет
Ол үшін
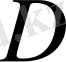 нүктесі бойынша 4 сырықтың моменттерінің тепе-теңдік теңдеуін жазайық:
нүктесі бойынша 4 сырықтың моменттерінің тепе-теңдік теңдеуін жазайық:
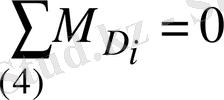 , (22)
, (22)
Ашық түрде :
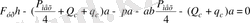 (23)
(23)
бұдан
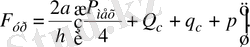 (24)
(24)
Егер
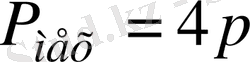 , онда
, онда
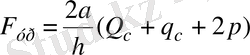 , (25)
, (25)
мұнадғы
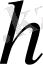 ұшбұрштан
ұшбұрштан
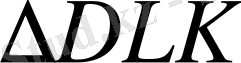 анықтаймыз:
DK=
1. 106м,
DL=
0. 205м болса, платформа биіктігі
анықтаймыз:
DK=
1. 106м,
DL=
0. 205м болса, платформа биіктігі
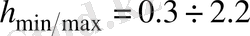 шектерінде өзгеретін болса, онда
KL
ұзындығы мына шекте өзгереді:
шектерінде өзгеретін болса, онда
KL
ұзындығы мына шекте өзгереді:
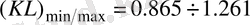 м.
м.
Онда берілген деректер бойынша
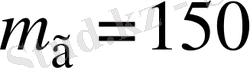 кг,
кг,
 кг,
кг,
 кг гидро цилиндр массасы
кг гидро цилиндр массасы
 кг, теңгеруші күшті анықтаймыз: жоғарғы күйде -
кг, теңгеруші күшті анықтаймыз: жоғарғы күйде -
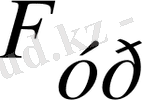 =
=
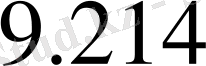 кН
,
төменгі күйде -
кН
,
төменгі күйде -
 =46. 362 кН
.
=46. 362 кН
.
Күштің ең жақсы берілуі В және Е топсаларын гидроцилиндрмен байланыстырғанда жүзеге асады, яғни
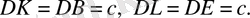 тең болғанда
тең болғанда
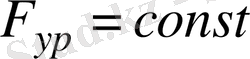 және
және
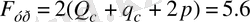 кН тең.
кН тең.
Бірақ бұл кезде
KL
мәні
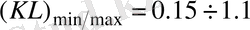 м шекте өзгереді, бұл конструкцияны күрделендыреды және көп сатылы телескопикалық конструкция құруды қажет етеді. Бір сатылы телескопикалық конструкция пайдалансақ, гидроцилиндр штогының қозғалысын қамтамасыз ету үшін
м шекте өзгереді, бұл конструкцияны күрделендыреды және көп сатылы телескопикалық конструкция құруды қажет етеді. Бір сатылы телескопикалық конструкция пайдалансақ, гидроцилиндр штогының қозғалысын қамтамасыз ету үшін
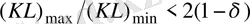 болу қажет, мұндағы
болу қажет, мұндағы
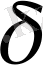 - қор коэффициенті
- қор коэффициенті
 .
.
яғни
 болғанда
болғанда
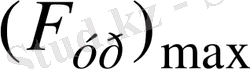 төменгі күйдегі ең аз мәні
төменгі күйдегі ең аз мәні
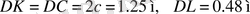 болғанда мүмкін, осы мәндерде
болғанда мүмкін, осы мәндерде
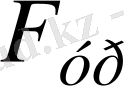 төменгі күйде мынаған тең 19. 6 кН, яғни біз анықтаған мәннен 2, 4 есе аз.
төменгі күйде мынаған тең 19. 6 кН, яғни біз анықтаған мәннен 2, 4 есе аз.
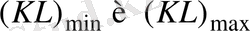 мәндері сәйкесінше 0. 786 м және 1. 571 м тең.
мәндері сәйкесінше 0. 786 м және 1. 571 м тең.
2. 3 Сыбайлас емес ҚССҚБ сұлбалы жүк көтеруші механизмнің гидроцилиндрлік тізбегін оптималдау
Алдыңғы бөлімде көрсетілгендей, жетекші кинематикалық тізбек (гидроцилиндр) сыбайлас сырықтарды байланыстырған кезде күштің берілуі өте тиымсыз болады. Сондықтан ары қарай жетекші кинематикалық тізбек сыбайдас емес сырықтарды байланыстыратын жетек сұлбасын қарастырамыз.
3. 1)
CG
буынымен сырғақты гидроцилиндр арқылы байланыстыру варианты.
9,
а
- суреттегі жүк көтеруші механизмді қарастырайық,
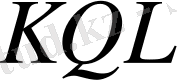 гидроцилиндрі 1 сырғақты
4
(
CG
) сырқпен байланыстырады.
гидроцилиндрі 1 сырғақты
4
(
CG
) сырқпен байланыстырады.
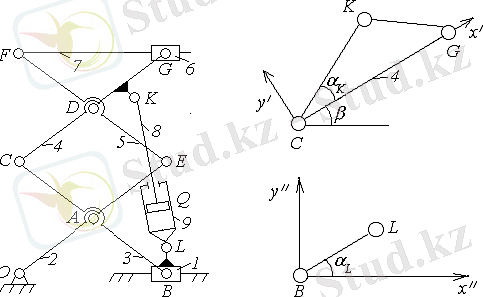
а ) б )
9 -сурет
а
) механизмнің кинематикалық сұлбасы,
б
) В сүйретпесі мен
СG
буыны бойынша
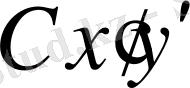 және
және
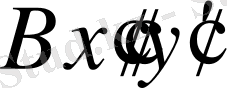 координаттар жүйесінің орналасуы.
координаттар жүйесінің орналасуы.
Берілген деректер төмендегідей:
1. Төменгі және жоғарғы күйдегі платформа биіктігі:
=0. 3м и
=2. 2м;
2. Буын жұптарының ұзындығы:
м;
3. Бір сырықтың массасы:
кг (сырықтың салмағы
) ;
4. жүк массасы (пайдалы жүктеме) :
кг (жүк салмағы
Н) ;
5. платформа массасы:
кг (жүк көтеруші платфрома салмағы
) ;
6. гидроцилиндр массасы:
кг ( гидроцилиндр салмағы
) .
Есептің мақсаты
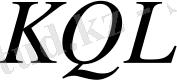 , гидроцилиндрінің оптималды орналасу күйін анықтау, яғни қай кезде механизмде оптималды күш берілісі орынайды, ол үшін
, гидроцилиндрінің оптималды орналасу күйін анықтау, яғни қай кезде механизмде оптималды күш берілісі орынайды, ол үшін
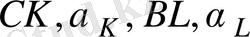 айнымалыларын (9,
б-сурет
) табу, сонымен қатар гидроцилиндрдегі күш
айнымалыларын (9,
б-сурет
) табу, сонымен қатар гидроцилиндрдегі күш
 ең аз болатындай
ең аз болатындай
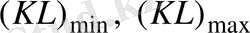 мәндерін табу.
мәндерін табу.
Платформа биіктігі
Н:
 ден
ден
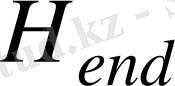 -ке дейін өзгергенде :
-ке дейін өзгергенде :
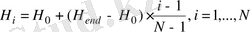 (26)
(26)
Механизімнің кинематикалық жұптарының
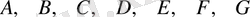 координаттары қозғалмайтын жүйе бойынша былай анықталады:
координаттары қозғалмайтын жүйе бойынша былай анықталады:
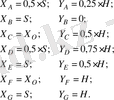 (27)
(27)
Айталық,
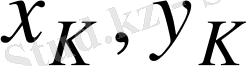 -
CG
буынымен (
-
CG
буынымен (
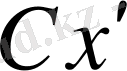 осьі
CG
бойымен бағытталған) қатаң байланысқан (қозғалмайтындай етіп)
осьі
CG
бойымен бағытталған) қатаң байланысқан (қозғалмайтындай етіп)
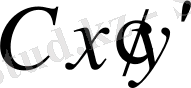 координат жүйесіне қатысты
К
топсасының локальді координаттары;
координат жүйесіне қатысты
К
топсасының локальді координаттары;
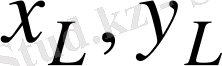 - ілгерлемелі қозғалатын сырғақпен қатаң байланысқан
- ілгерлемелі қозғалатын сырғақпен қатаң байланысқан
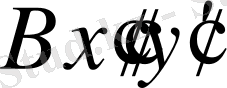 (9, б-сурет) координаттар жүйесіне қатысты
L
топсаның локалды координаттары. Онда
L
және
К
кинематикалық жұптарының абсолютті координаттары былай анықталады:
(9, б-сурет) координаттар жүйесіне қатысты
L
топсаның локалды координаттары. Онда
L
және
К
кинематикалық жұптарының абсолютті координаттары былай анықталады:
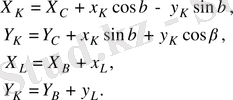 (28)
(28)
Берілген күйдегі цилиндрдің ұзындығы мына формуламен анықталады.
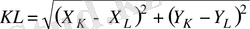 (29)
(29)
Күштің берілісін көрсететін критериді минималдай отырып, гидроцилиндрдегі минимум күшті аламыз:
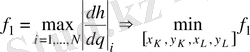 . (30)
. (30)
Мұндағы i=1, . . . , N механизімнің N орнын (төменнен жоғарыға қарай) білдіреді.
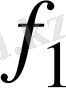 мәнін мына формуламен аламыз
мәнін мына формуламен аламыз
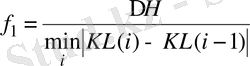 , (31)
, (31)
Мұндағы
 . мысалы
. мысалы
 =0, 3м,
=0, 3м,
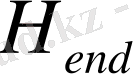 =2, 2м болғанда, N=44 болса, ΔΗ=
=2, 2м болғанда, N=44 болса, ΔΗ=
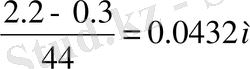
Соның ішінде конструктивті шектеулерді ескеру қажет (қосымша шарт)
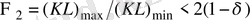 , (32)
, (32)
мұндағы
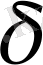 - қор коэффициенті.
- қор коэффициенті.
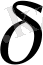 -ның мәні неғұрлым көп болғаны жақсы. .
-ның мәні неғұрлым көп болғаны жақсы. .
Варияциялық айнымалылардың мәнін
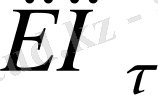 -тізбектей генераторының көмегімен іздеу аумағында бір қалыпты таратылған күйде өзгертіп отырамыз.
-тізбектей генераторының көмегімен іздеу аумағында бір қалыпты таратылған күйде өзгертіп отырамыз.
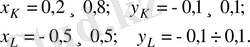 (33)
(33)
Ол үшін
 [ ] бағдарламасы қолданылады.
[ ] бағдарламасы қолданылады.
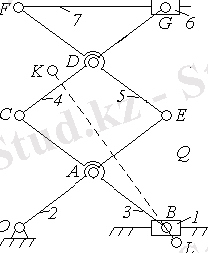
‘566’ номерлі собол нүктесіне
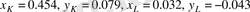 параметрлері сай. Оның кинематикалық сұлбасы 10,
а-
суретте, ал 10,
б
-суретте
параметрлері сай. Оның кинематикалық сұлбасы 10,
а-
суретте, ал 10,
б
-суретте
 тәуелділік графигі көрсетілген. Көріп тұрғанымыздай график сызықтыға жақын. .
тәуелділік графигі көрсетілген. Көріп тұрғанымыздай график сызықтыға жақын. .
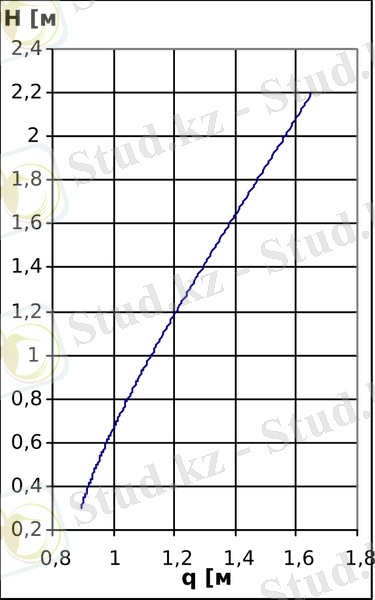
 (
б
) тәуелділігінің графигі.
(
б
) тәуелділігінің графигі.
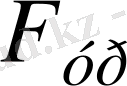 =12. 252кН (1250 кгС) максимал мәні төмен жетекті сұлбамен салыстырғанда 3, 8 есе аз. Жоғары күйде
=12. 252кН (1250 кгС) максимал мәні төмен жетекті сұлбамен салыстырғанда 3, 8 есе аз. Жоғары күйде
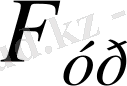 =6. 861кН (700 кгС) .
=6. 861кН (700 кгС) .
Бірақ ары қарайғы
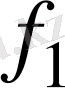 мәнінің төмендеуі конструктивті шектің нашарлауына алып келеді.
мәнінің төмендеуі конструктивті шектің нашарлауына алып келеді.
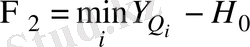 шектеуі 0, 3 мәнінен үлкен (10,
б-
сурет) . Сондықтан келесі іздеу анықталған шектің ішінде жүргізіледі.
шектеуі 0, 3 мәнінен үлкен (10,
б-
сурет) . Сондықтан келесі іздеу анықталған шектің ішінде жүргізіледі.
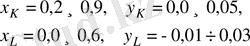 (35)
(35)
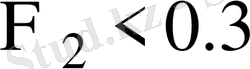 -ті қалағанбыз.
-ті қалағанбыз.
параметрлер мәні 2 кестеде келтірілген.
а )
Алынған 12 механизмдердің ішіндегі Соболь нүктесінің ‘1527’ және ’1597’ номерлі механизм алынды. Механизмнің кинематикалық сұлбасы 14-ші суретте көрсетілген.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz