Жалпыланған тригонометриялық және гиперболалық функциялар: бөлшек ретті дифференциалдық теңдеулерді шешудегі қолдану


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:
Ф-ОБ-001/033
Қазақстан Республикасы Білім және ғылым министрлігі
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
«Қорғауға жіберілді»
Кафедра меңгерушісі,
техн. ғ. д., профессор
Ә. Мұратов
«___»2011ж
Д И П Л О М Д Ы Қ Ж Ұ М Ы С
Тақырыбы: Жалпыланған тригонометриялық, гиперболалық функциялар
және оларды кейбір дифференциалдық теңдеулерді
шешуде қолдану
050109-«Математика» мамандығы бойынша
Орындаған: Надильбекова Л. М.
Ғылыми жетекшісі,
магистр-оқытушы Төребек Б. Т.
Түркістан 2011
МАЗМҰНЫ
КІРІСПЕ . . . 3
1. Бөлшек ретті операторлар анықтамасы, қасиеттері және кейбір арнайы функциялар.
1. 1 Бөлшек ретті операторлар анықтамасы және кейбір қасиеттері . . . 10
1. 2 Кейбір функциялардың қатарға жіктелуі және кейбір арнайы функ-циялар . . . 20
2. Жалпыланған тригонометриялық, гиперболалық функциялар және олардың кейбір дифференциалдық теңдеулерді шешуде қолданылуы
2. 1 Жалпыланған тригонометриялық функциялар және олардың кейбір бөлшек ретті дифференциалдық теңдеулерді шешуде қолданылуы . . . 32
2. 2 Жалпыланған гиперболалық функцияларды енгізу және кейбір бөлшек ретті дифференциалдық теңдеулерді шешуде қолдану . . . 36
2. 3. Жалпыланған тригонометриялық және гиперболалық функциялардың графиктері . . . 45
Қорытынды . . . 58
Пайдаланған әдебиеттер . . . 59
КІРІСПЕ
Дипломдық жұмыста тригонометриялық және гиперболалық функциялардың дәрежелік қатар көріністегі жалпыланған формасы енгізіліп, олардың кейбір бөлшек ретті дифференциалдық теңдеулердің шешімі болатындығы көрсетіледі.
Бөлшек ретті туынды және интегралдың көптеген анықтамалары бар. Оларды Риман, Лиувилль, Риман - Лиувилль, Капуто, Джрбашян, Вейл, Грюнвальд - Летников, Адамар, Маршо, Адамар - Маршо, Колванкар, Росс-Миллер, Эрдеи - Кобер, Джрбашян - Нерсесян тағы басқа мағыналарда қарастыруға болады.
Соңғы жылдары бөлшек ретті туынды қатысқан дифференциалдық теңдеулерді зерттеуге арналған көптеген әдебиеттер баспадан шығып, түрлі ғылыми мақалалар журналдарда жарық көруде. Мысалы, А. М. Нахушевтің [1, 4], С. Г. Самко, А. А. Килбас, О. И. Маричевтің [2], М. М. Джрбашянның [3], М. М. Джрбашян, А. Б. Нерсесянның [10], А. В. Псхудың [5], И. Подлубныйдың [8], Б. Х. Турметовтің [15-20] және т. б. ғалымдардың [7, 9, 11-14] еңбектерін жатқызуға болады.
Бөлшек ретті операторлардың физика мен техникада қолданылуына арналған әдебиеттердің мысалы ретінде [6, 21, 25] ғылыми еңбектерді атауға болады.
Жұмыстың мақсаты : Жұмыстың негізгі мақсаты жалпыланған тригонометриялық және гиперболалық функцияларды дәрежелік қатардың көмегімен енгізу. Алынған қатарлардыңдың кейбір қасиеттерін зерттеп, олардың бүтін, бөлшек ретті туындыларын есептеу және кейбір бөлшек ретті дифференциалдық теңдеулердің шешімі болатынын көрсету.
Зерттеу әдістері : Бөлшек ретті дифференциалдық теңдеулерде туындысымен қатар интегралда беріледі. Сондықтан бөлшек ретті дифференциалдық теңдеулерді теңдеулер ретінде қарастыруға да болады. Бұл теңдеулерді шешуде негізінен операциялық есептеу, Фурье, Лаплас түрлендірулері, функционалдық және математикалық талдау әдістері көп қолданылады. Бұл дипломдық жұмыста бөлшек ретті дифференциалдық теңдеулерді шешу операторлық әдіс арқылы жүзеге асырылады.
Дипломдық жұмыстың құрылымы: Диплом жұмысы кіріспе, негізгі бөлім, қорытынды және әдебиеттер тізімінен тұрады. Негізгі бөлім екі тарау, жеті параграфтан тұрады.
Бірінші тараудың бірінші, екінші параграфтарында бөлшек ретті операторлардың анықтамалары беріліп, кейбір қасиеттері көрсетіледі. Үшінші параграфта тригонометриялық, гиперболалық функциялардың дәрежелік қатарға жіктелуі беріліп, кейбір дифференциалдық теңдеулердің шешімін қатардың көмегімен табуға болатындығы айтылады.
Екінші тарауда жалпыланған тригонометриялық, гиперболалық функциялар дәрежелік қатардың көмегімен енгізіліп, қасиеттері зерттелінеді. Алынған функциялардың кейбір бөлшек ретті дифференциалдық теңдеулердің шешімі болатындығы көрсетіледі. Тараудың соңында жалпыланған тригонометриялық және гиперболалық функциялардың кейбір дербес жағдайлардағы графиктері математикалық есептерді шешуде қолайлылық тудыратын «Марlе» компьютерлік бағдарламасы бұрықтары көмегімен жүзеге асырылған.
Дипломдық жұмыстың негізгі нәтижелері:
Алдымен тригонометриялық функцияларға туралы мәліметтерді келтірейік. Бізге математикалық талдау пәнінен тригонометриялық функциялардың төмендегідей қатарға жіктелетіні белгілі [22, 24] :
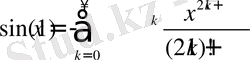
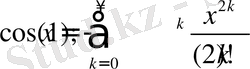
Енді біз осы функциялардың жалпыланған түрін анықтайық.
0≤α<1 болсын. Онда жалпыланған синусты төмендегідей түрде анықтаймыз:

Егер α=0, ⇒
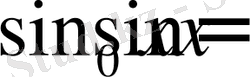
Жалпыланған синусқа сәйкес жалпыланған косинустың анықтамасын береміз:

Егер α=0, ⇒
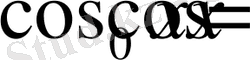
Бөлшек ретті туынды қатысқан теңдеулер және есептердің шешімдері көп жағдайда Миттаг-Леффлердің атымен аталатын
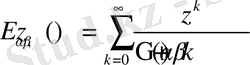
функция арқылы өрнектеледі. Біз жоғарыда қарастырған жалпыланған тригонометриялық функцияларды Миттаг-Леффлер түріне келтіруге болады.
Жалпыланған тригонометриялық функциялар мен Миттаг-Леффлер функциясы арасында мына қатынастар орынды
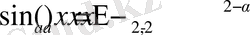
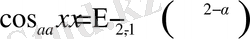
Жалпыланған тригонометриялық функциялардың туындысы зерттеу арқылы олардың кейбір дифференциалдық теңдеулердің шешімі болатынын көрсетуге болады.
Жалпыланған тригонометриялық функциялардың бүтін және бөлшек ретті туындыларын қарастырсақ мына нәтижелер орынды:
Жалпыланған синус және жалпылаңған косинус функциялары үшін
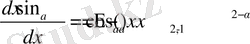 ,
,
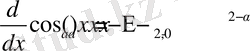
Демек, жалпыланған синустың туындысы жалпыланған косинус болады. Ал, жалпыланған косинустың туындысы жалпыланған синус болмайды екен. Ол тек
 болғанда ғана орындалады.
болғанда ғана орындалады.
Енді біз өзіміз енгізген жалпыланған тригонометриялық функциялар арқылы өрнектелетін
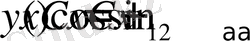 (1)
(1)
функцияны қарастырайық.
Мұнда
 болса, онда
болса, онда
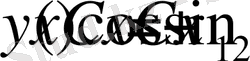
Ал, бұл функция
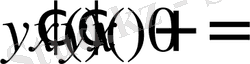
теңдеуінің жалпы шешімі болады.
Осы сияқты (1) теңдігімен анықталған
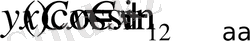 функциясы
функциясы
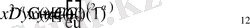
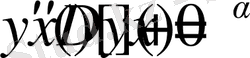
теңдеуінің шешімі болып табылады. Мұндағы
 ,
,
 - тұрақты коэффиценттер.
- тұрақты коэффиценттер.
2)
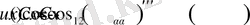 (2)
(2)
(мұндағы
 ,
,
 - тұрақты коэффиценттер) деп алсақ, онда бұл функция
- тұрақты коэффиценттер) деп алсақ, онда бұл функция
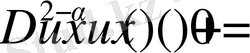
теңдеуінің шешімі болады.
3)
 (3)
(3)
функциясы
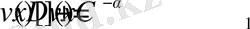

теңдеулерінің шешімі болады.
Жалпыланған гиперболалық функциялар
Бізге
 ,
,
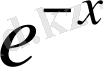 ,
,
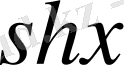 және
және
 функцияларының қатар көріністе жазылуы бұрыннан белгілі. Яғни,
функцияларының қатар көріністе жазылуы бұрыннан белгілі. Яғни,
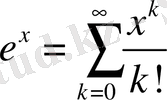
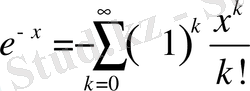
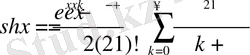
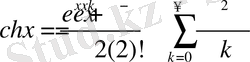
болсын.
Енді біз осы функцияларға сәйкес келетін жалпыланған гиперболалық функцияларын табамыз.
Айталық,
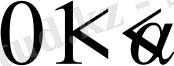 болсын . Осы санға сәйкес келетін мына
болсын . Осы санға сәйкес келетін мына
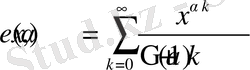 (4)
(4)
функцияны қарастырыйық. (4) қатардың бірқалыпты жинақталуынан осы қатарда
 бойынша шекке көшсек, онда
бойынша шекке көшсек, онда
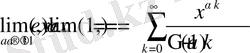
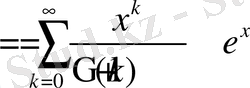 Equation. DSMT4
Equation. DSMT4
Осы сияқты
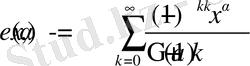
функцияны қарастырып, α=1 болғанда
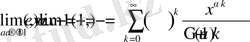
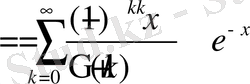
теңдігін аламыз.
1-теорема. Жалпыланған гиперболалық функциялар үшін мына теңдіктер орынды:
1)
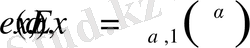
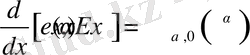 ;
;
2)

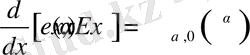
3)
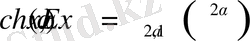 ,
,
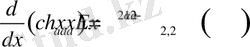
4)
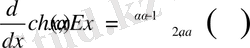
Келесі түрдегі функцияларды қарастырамыз
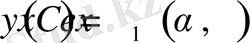 (5)
(5)
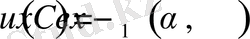 . (6)
. (6)
Онда бұл функциялар
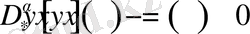 (7)
(7)
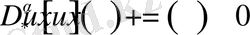 (8)
(8)
түрдегі бөлшек ретті дифференциалдық теңдеуінің жалпы шешімі болады. Бұл тұжырымды дәлелдеу үшін жоғарыда келтірілген жалпыланған оң және теріс дәрежелі экспоненталардың бөлшек ретті туындыларынан өзінің шығатынын көрсетсек жеткілікті.
Жоғарыда алынған нәтижелерді қорыта келе келесі түрдегі теореманы дәлелдей аламыз.
2-т
еорема.
Егер
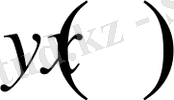 функциясының бірінші ретті туындысы бар, үзіліссіз болса және оны дәрежелік қатар түрінде жазуға болатын болса, онда (7) дифференциалдық теңдеуі үшін
функциясының бірінші ретті туындысы бар, үзіліссіз болса және оны дәрежелік қатар түрінде жазуға болатын болса, онда (7) дифференциалдық теңдеуі үшін
 (9)
(9)
шартымен берілген есептің шешімі бар және келесі түрде жазылады
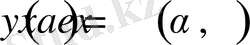
3-теорема .
Егер
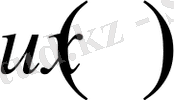 функциясының бірінші ретті туындысы бар, үзіліссіз болса және оны дәрежелік қатар түрінде жазуға болатын болса, онда (8) дифференциалдық теңдеуі үшін
функциясының бірінші ретті туындысы бар, үзіліссіз болса және оны дәрежелік қатар түрінде жазуға болатын болса, онда (8) дифференциалдық теңдеуі үшін
 (9) *
(9) *
шартымен берілген есептің шешімі бар және келесі түрде жазылады
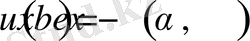
1. Бөлшек ретті операторлар анықтамасы, қасиеттері және кейбір арнайы функциялар.
1. 1. Бөлшек ретті туынды анықтамасы және оның кейбір қасиеттері
Айталық,
 - кейбір нақты сан болсын.
- кейбір нақты сан болсын.
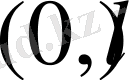 ,
,
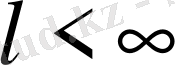 интервалда берілген
интервалда берілген
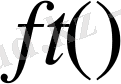 функциясы үшін келесі операторды қарастырамыз
функциясы үшін келесі операторды қарастырамыз
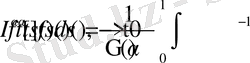 ,
,
мұндағы
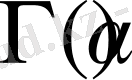 - Эйлердің гамма функциясы,
- Эйлердің гамма функциясы,
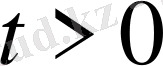 .
.
Берілген оператор
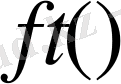 функциясының Риман - Лиувилль мағынасындағы бөлшек ретті интегралдау операторы деп аталады [1-2] .
функциясының Риман - Лиувилль мағынасындағы бөлшек ретті интегралдау операторы деп аталады [1-2] .
Айталық
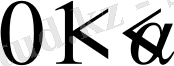 болсын және
болсын және
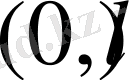 аралығында анықталған қандай да бір
аралығында анықталған қандай да бір
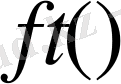 функциясы берілсін дейік.
функциясы берілсін дейік.
Анықтама 1.
Берілген α саны және
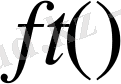 функциясы үшін Риман - Лиувилл мағынасындағы бөлшек ретті дифференциалдау операторы деп,
функциясы үшін Риман - Лиувилл мағынасындағы бөлшек ретті дифференциалдау операторы деп,
 (1. 1. 1)
(1. 1. 1)
өрнекпен берілген формуланы айтамыз.
Анықтама 2.
Берілген α саны және
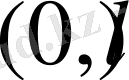 интервалында 1-ретті туындыға ие болатын
интервалында 1-ретті туындыға ие болатын
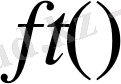 функциясы үшін Капуто мағынасындағы бөлшек ретті дифференциалдау операторы деп
функциясы үшін Капуто мағынасындағы бөлшек ретті дифференциалдау операторы деп
 (1. 1. 2)
(1. 1. 2)
өрнекпен берілген формуланы айтамыз.
Бөлшек ретті туынды операторларының қолданылуы жайлы бірнеше мысалдар келтірейік. Себебі, біздің алдағы зерттеулерімізде бөлшек ретті туынды операторлардың алатын орны ерекше.
1- м ысал .
1. Тұрақтының интегралы.
 болсын. Онда
болсын. Онда
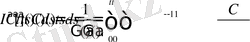

Демек,
 болса, онда
болса, онда
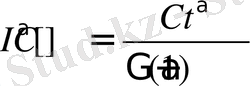 .
.
Дербес жағдайлары:
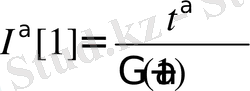 ,
,
 .
.
2. Дәрежелік функцияның интегралы.
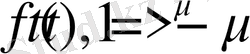 болсын. Онда
болсын. Онда

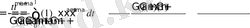
Демек,
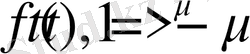 болса, онда
болса, онда
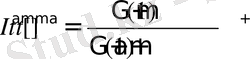
2-мысал.
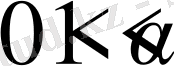 болсын дейік.
болсын дейік.
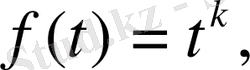
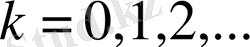 функциясы үшін
функциясы үшін
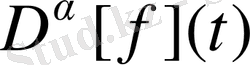 мәнін есептейміз.
мәнін есептейміз.
 - операторының анықтамасы бойынша
- операторының анықтамасы бойынша
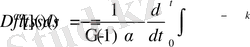
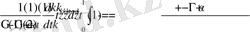
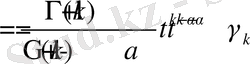 .
.
мұндағы
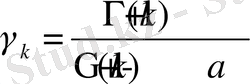 .
.
3-мысал.
Айталық,
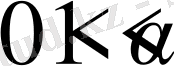 болсын.
болсын.
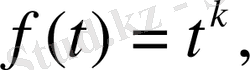
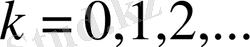 функциясы үшін
функциясы үшін
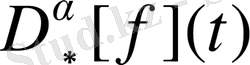 мәнін есептейміз.
мәнін есептейміз.
 болғанда Капуто мағынасындағы бөлшек ретті дифференциалдау операторының анықтамасынан
болғанда Капуто мағынасындағы бөлшек ретті дифференциалдау операторының анықтамасынан
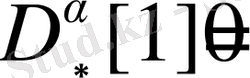
болатыны айқын көрініп тұр.
 болсын. Онда анықтама бойынша
болсын. Онда анықтама бойынша
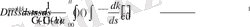
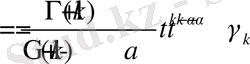
Демек,
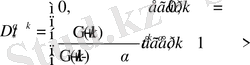
Жалпы айтқанда, бұл мысалдардан дифференциалданатын функциялар үшін
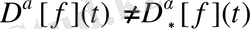
болатындығы келіп шығады.
Бөлшек ретті операторлардың кейбір қасиеттері.
1-қасиет :
Кез келген
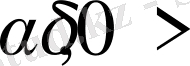 сандары үшін
сандары үшін
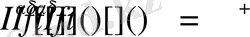 (1. 1. 3)
(1. 1. 3)
теңдігі орынды.
Дәлелдеуі: Бөлшек ретті интегралдың анықтамасы бойынша (1. 1. 3) теңдігінің сол жағындағы өрнекті
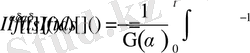
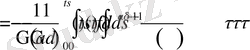
түрінде жазып аламыз.
Соңғы алынған интегралдардың орнын ауыстыратын болсақ, онда

интегралы
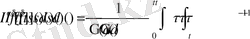
көріністе жазылады.
Енді ішкі интегралды есептейік. Бұл интегралды есептеу үшін интегралда айнымалы
 түрінде алмастырайық. Осы алмастыру нәтижесінде ішкі интеграл
түрінде алмастырайық. Осы алмастыру нәтижесінде ішкі интеграл
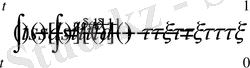

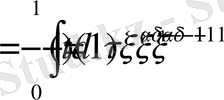
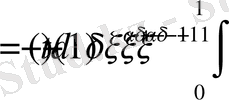
түрге келеді.
Ал мұндағы
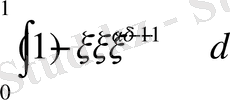
интегралы Эйлердің бета функциясы болғандықтан бастапқы
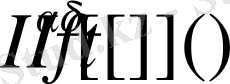 интегралы
интегралы
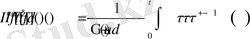
көрініске келеді.
Онда, Риман-Лиувилл мағынасындағы интегралдың анықтамасы бойынша соңғы теңдіктің оң жағындағы интеграл
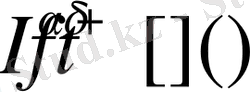 функциясына тең.
функциясына тең.
Нәтижеде
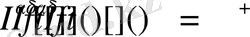
теңдігі орынды екеніне көз жеткіземіз.
2-қасиет :
Егер
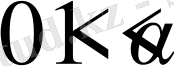 және
және
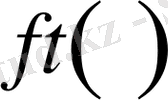 функция (0,
l
) аралықта α - ретті туындыға ие болса, онда
функция (0,
l
) аралықта α - ретті туындыға ие болса, онда
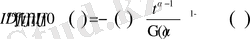 (1. 1. 6)
(1. 1. 6)
теңдік барлық жерде дерлік орынды.
Дәлелдеуі : (4) - теңдікті дәлелдеу үшін қарастырылатын интегро-дифференциалдық операторлардың анықтамасынан пайдаланамыз.
Анықтама бойынша
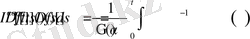
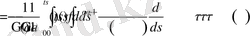
Соңғы алынған теңдіктегі ішкі интеграл анықтама бойынша Риман-Лиувилдің
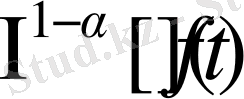 интегралдау операторын береді.
интегралдау операторын береді.
Олай болса, бұл теңдік мына түрге келеді
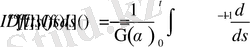
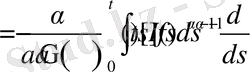
Бұл алынған өрнекті төмендегіше жазып алып,
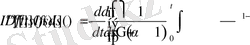
Бұл теңдіктегі ішкі интегралды
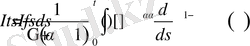
түрінде жазып алып, оны есептейіқ.
Интегралды есептеу үшін бөліктеп интегралдау әдісін қолданамыз.
Осы әдіс бойынша
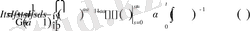
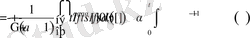
Демек,


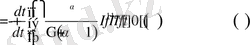
болады. Соңғы алынған нәтижеге 1-қасиетті қолдансақ, онда мұны
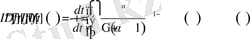
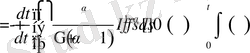
түрінде жазамыз. Сонғы интегралды t бойынша дифференциалдайық
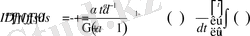
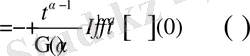
Демек,
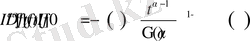
теңдік орынды екенін көреміз.
3-қасиет :
Кез-келген
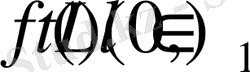 функциясы және
функциясы және
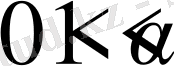 саны үшін
саны үшін
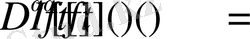 (1. 1. 7)
(1. 1. 7)
теңдік орынды.
Дәлелдеуі: Бөлшек ретті интеграл және дифференциалдаудың анықтамасы бойынша
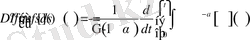

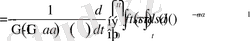
Соңғы алынған өрнектегі ішкі интегралға
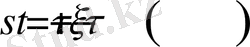 алмастыруын енгізіп, бөлек есептеп алайық.
алмастыруын енгізіп, бөлек есептеп алайық.
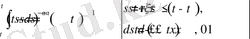
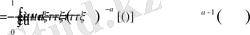
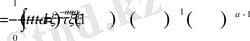
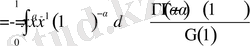
Демек,

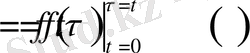
тең болады. Олай болса кез келген
 функциясы және
функциясы және
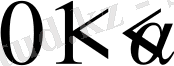 сандары үшін
сандары үшін
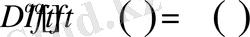
теңдігі орынды екені шығады .
Енді Риман-Лиувилл мағынасындағы бөлшек ретті дифференциалдау операторы мен Капуто мағынасындағы дифференциалдау операторы арасындағы байланысты қарастырайық.
4-қасиет:
Егер
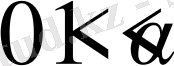 және
f(t)
функция (0,
l
) интервалда бірінші ретті туындыға ие болса, онда
және
f(t)
функция (0,
l
) интервалда бірінші ретті туындыға ие болса, онда
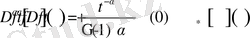 (1. 1. 8)
(1. 1. 8)
теңдік барлық жерде дерлік орынды .
Дәлелдеуі: Бөлшек ретті туындының анықтамасы бойынша
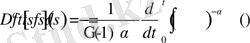
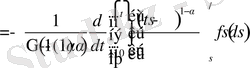
болады. Енді соңғы нәтижені бөліктеп интегралдайық.
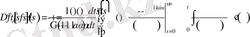

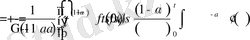
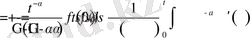
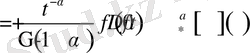
Демек,
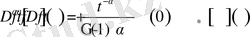
орындалады.
5-қасиет:
Егер
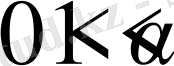 және
f(t)
функция (0,
l
) интервалда бірінші
және
f(t)
функция (0,
l
) интервалда бірінші
ретті туындыға ие болса, онда
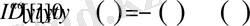 (1. 1. 9)
(1. 1. 9)
теңдік барлық жерде дерлік орынды .
Дәлелдеуі:
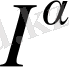 және
және
 операторларының анықтамасын пайдаланып келесіні аламыз
операторларының анықтамасын пайдаланып келесіні аламыз
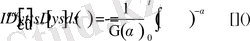
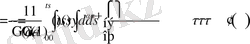
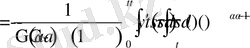
Соңғы өрнектегі ішкі интегралды есептейік:
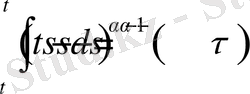

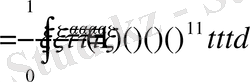
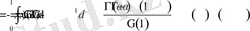
Демек,
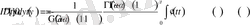
теңдігі орынды болады.
1. 2. Кейбір функциялардың қатарға жіктелуі және кейбір арнайы функциялар.
Берілген ақырсыз
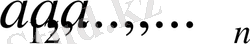 , мұндағы
а
n
=f(n)
сандық тізбегінің мүшелерін біріктіргенде шығатын символ
, мұндағы
а
n
=f(n)
сандық тізбегінің мүшелерін біріктіргенде шығатын символ
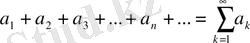 (1. 2. 1)
(1. 2. 1)
сандық қатар, ал
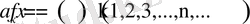 сандары қатардың мүшелері деп аталады.
сандары қатардың мүшелері деп аталады.
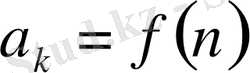 -қатардың жалпы мүшесі дейміз. Енді (1. 2. 1) қатардың мүшелерінен дербес қосындылар деп аталатын қосындылар тізбегін құралық:
-қатардың жалпы мүшесі дейміз. Енді (1. 2. 1) қатардың мүшелерінен дербес қосындылар деп аталатын қосындылар тізбегін құралық:
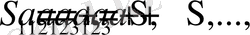
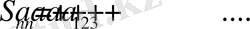
Егер
 дербес қосынды
дербес қосынды
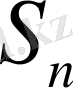 -нің арқылы шегі бар болса, яғни
-нің арқылы шегі бар болса, яғни
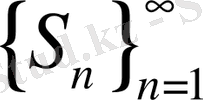 санды тізбегінің S-ке тең нақты мәнді шегі бар болса, онда (1. 2. 1) қатар жинақталады, S саны (1. 2. 1) қатардың қосындысы дейді де
санды тізбегінің S-ке тең нақты мәнді шегі бар болса, онда (1. 2. 1) қатар жинақталады, S саны (1. 2. 1) қатардың қосындысы дейді де
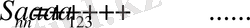
деп жазады. Бұл жағдайда (1. 2. 1) қатар S- санына жинақталады деп айтады. Қалған жағдайлардың әрқайсысында, яғни
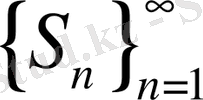 тізбегінің +∞, -∞ не ∞ ақырсыз шектері бар, не ешқандай да шегі болмағанда, (1. 2. 1) қатар жинақталмайды, не жинақсыз деп аталады.
тізбегінің +∞, -∞ не ∞ ақырсыз шектері бар, не ешқандай да шегі болмағанда, (1. 2. 1) қатар жинақталмайды, не жинақсыз деп аталады.
Енді жинақталатын сандық қатарлардың негізгі қасиеттерін келтірейік.
1. Егер сандық қатар
 жинақталса, онда оның
жинақталса, онда оның
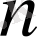 -ші қалдығы деп аталатын мынадай
-ші қалдығы деп аталатын мынадай
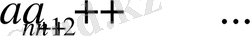 қатарының қосындысы нөлге ұмтылады. Дәлірек айтқанда, егер қатар жинақталса, онда
қатарының қосындысы нөлге ұмтылады. Дәлірек айтқанда, егер қатар жинақталса, онда
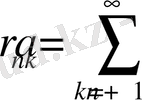 тәртібі бойынша анықталған
тәртібі бойынша анықталған
 тізбегі мағыналы болып
тізбегі мағыналы болып
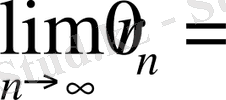 теңдігі орындалады.
теңдігі орындалады.
2. Егер
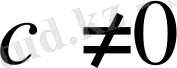 саны берілсе, онда
саны берілсе, онда
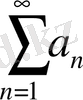 және
және
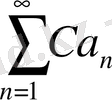 қатарлары не бірдей жинақталады, не бірдей жинақталмайды. Олар жинақталған жағдайда
қатарлары не бірдей жинақталады, не бірдей жинақталмайды. Олар жинақталған жағдайда
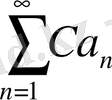 қатарының қосындысы
қатарының қосындысы
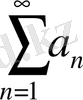 қатарының қосындысымен С санының көбейтіндісіне тең.
қатарының қосындысымен С санының көбейтіндісіне тең.
3. Қатар
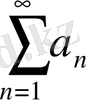 және
және
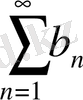 қатарлары жинақталса, онда
қатарлары жинақталса, онда
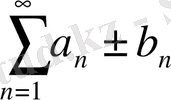 .
.
4. Қатар жинақталуы үшін оның әр қалдық қатары жинақталуы қажетті және жеткілікті.
5. Егер сандық қатар жинақталса, онда оның жалпы мүшесінің жалпы шегі бар және ол нөлге тең.
Егер қатардың жалпы мүшесі нөлге ұмтылса, онда қатар жинақталмайды (қатардың жинақталмауының жеткілікті шарты) .
Шынында да қатар жинақталса, онда оның жалпы мүшесі нөлге ұмтылар еді. Сонымен,
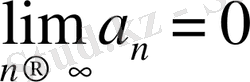 шарты қатардың жинақталуының қажетті шарты бола тұрып, жеткілікті шарты емес. Қатардың жалпы мүшесі нөлге ұмтылса да, қатардың жинақталмауы да мүмкін.
шарты қатардың жинақталуының қажетті шарты бола тұрып, жеткілікті шарты емес. Қатардың жалпы мүшесі нөлге ұмтылса да, қатардың жинақталмауы да мүмкін.
1-мысал. Гармоникалық қатар
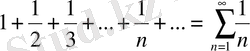
жинақталмайды, ал бірақ та
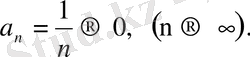
2-мысал. Мынадай қатар:
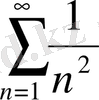 жинақталады және де
жинақталады және де
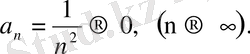
Теріс емес мүшелі қатардың жинақталу және жинақталмау белгілері.
1. Салыстыру белгісі .
А. Егер белгілі бір
 және
және
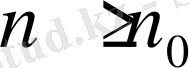 болғанда
болғанда
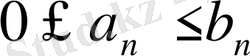 болса, онда:
болса, онда:
а)
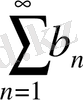 қатары жинақталғанда
қатары жинақталғанда
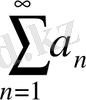 қатары жинақталады.
қатары жинақталады.
б)
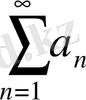 қатары жинақталғанда
қатары жинақталғанда
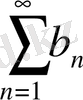 қатары да жинақталады.
қатары да жинақталады.
Б. Егер
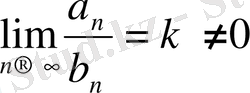 болса, онда
болса, онда
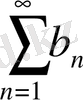 және
және
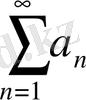 қатарларының не екеуі бірдей жинақталмайды, не екеуі де бірдей жинақталады.
қатарларының не екеуі бірдей жинақталмайды, не екеуі де бірдей жинақталады.
2.
Даламбер белгісі
. Оң мүшелі
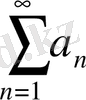 қатар үшін
қатар үшін
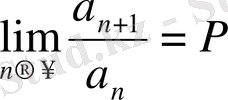 бар болса, онда
бар болса, онда
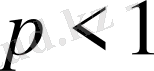 болғанда қатар жинақталады,
болғанда қатар жинақталады,
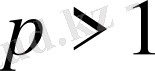 болғанда қатар жинақталмайды,
болғанда қатар жинақталмайды,
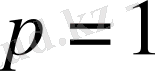 болғанда қатардың жинақталуы да, жинақталмауы да мүмкін, яғни белгісіз.
болғанда қатардың жинақталуы да, жинақталмауы да мүмкін, яғни белгісіз.
3.
Коши белгісі
. Теріс емес мүшелі
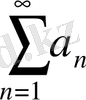 қатары беріліп
қатары беріліп
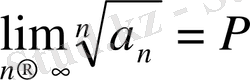 шегі бар болсын. Бұл жағдайда:
шегі бар болсын. Бұл жағдайда:
а) егер
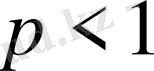 болса, онда қатар жинақталады;
болса, онда қатар жинақталады;
б) егер
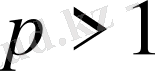 болса, онда қатар жинақталмайды;
болса, онда қатар жинақталмайды;
в) егер
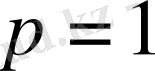 болса, онда қатардың жинақталуы не жинақталмауы жөнінде ештеңе айта алмаймыз, яғни
болса, онда қатардың жинақталуы не жинақталмауы жөнінде ештеңе айта алмаймыз, яғни
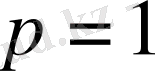 болатындай жинақталатын да, жинақталмайтын да қатарлар бар.
болатындай жинақталатын да, жинақталмайтын да қатарлар бар.
4. Кошидің интегралдық белгісі .
Егер қатар
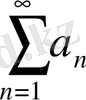 (А)
(А)
беріліп, сонымен бірге
 мәндері үшін анықталған, үзіліссіз, оң және бір санды кемімелі
мәндері үшін анықталған, үзіліссіз, оң және бір санды кемімелі
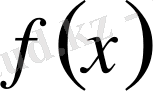 функциясы үшін кейбір
функциясы үшін кейбір
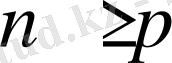 нөмірінен бастап
нөмірінен бастап
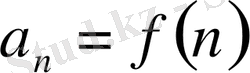 теңдігі орындалып, меншіксіз интеграл
теңдігі орындалып, меншіксіз интеграл
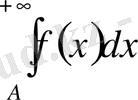 (В)
(В)
жинақталса, онда (А) қатары жинақталады, ал егер (В) интеграл жинақталмаса, онда (А) қатары да жинақталмайды.
Мүшелерінің таңбалары әртүрлі болып келген қатарлар. ауыспалы таңбалы қатарлар.
1.
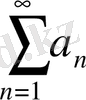 сандық қатары берілсін. Егер осы қатардың әр мүшесін оның абсолюттік шамасына алмастырғанда пайда болатын теріс емес мүшелі
сандық қатары берілсін. Егер осы қатардың әр мүшесін оның абсолюттік шамасына алмастырғанда пайда болатын теріс емес мүшелі
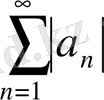
қатары жинақталса, онда
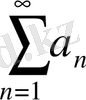 қатары абсолютті жинақталады дейді.
қатары абсолютті жинақталады дейді.
Абсолютті жинақталатын қатар жинақталады. Бұған кері тұжырым орындалу мүмкін емес.
Егер
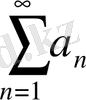 қатары жинақталып,
қатары жинақталып,
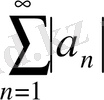 қатары жинақталмаса, онда
қатары жинақталмаса, онда
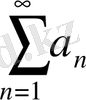 абсолютті емес не шартты жинақталады деп аталады.
абсолютті емес не шартты жинақталады деп аталады.
2. Лейбниц белгісі . Егер таңбасы ауыспалы
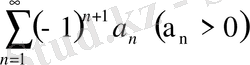 (С)
(С)
1)
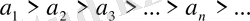 ,
,
2)
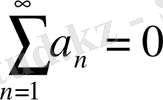 болса, онда (С) қатары жинақталады.
болса, онда (С) қатары жинақталады.
Дәрежелік қатар.
Бұл параграфта дәрежелік қатар деп аталатын функциялық қатарлардың бір дербес түрін қарастырамыз. Сандық тізбек беріліп
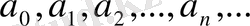 және
х
тәуелсіз айнымалы болса, онда
және
х
тәуелсіз айнымалы болса, онда
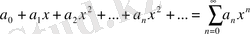 (1. 2. 2)
(1. 2. 2)
түріндегі қатар дәрежелік қатар деп аталады. Дәрежелік қатардың жалпыланған түрі
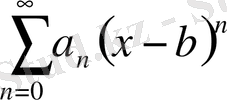 (1. 2. 3)
(1. 2. 3)
болып табылады. Алайда, (1. 2. 3) қатарда
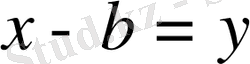 алмастыру жасасақ, онда (1. 2. 2) түрдегі қатарға келтіреміз. Сондықтан дәрежелік қатар жайындағы мәселені тек (1. 2. 2) түрдегі қатар үшін қарастырамыз. Егер (1. 2. 2) дәрежелік қатар
алмастыру жасасақ, онда (1. 2. 2) түрдегі қатарға келтіреміз. Сондықтан дәрежелік қатар жайындағы мәселені тек (1. 2. 2) түрдегі қатар үшін қарастырамыз. Егер (1. 2. 2) дәрежелік қатар
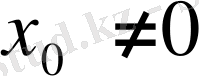 нүктесінде жинақталса, ол қатар х-тің
нүктесінде жинақталса, ол қатар х-тің
 қанағаттандыратын барлық мәндерінде абсолютті жинақталады.
қанағаттандыратын барлық мәндерінде абсолютті жинақталады.
Дәрежелік қатардың (1. 2. 2) жинақталу облысы центрі сандар облысының санау басында жатқан (-r; r) аралығы болады; сонымен бірге бұл аралықтың ішінде (1. 2. 2) қатар абсолютті жинақталада. Жинақталық интервалының радиусын
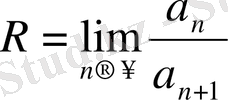 немесе
немесе
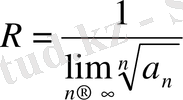
Формуласының көмегімен тауып, (1. 2. 2) қатардың жинақтылық интервалы (-r; r) деп жазылады.
Мысалдар: 1)
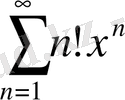 қатарының жинақталу интервалын табу керек.
қатарының жинақталу интервалын табу керек.
Шешуі: Бұл қатар үшін
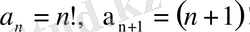 . Жинақтылық қатарының радиусы
. Жинақтылық қатарының радиусы
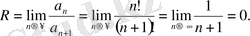
Демек, қатар x=0 нүктесінде ғана жинақталады.
2)
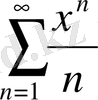 қатары үшін
қатары үшін
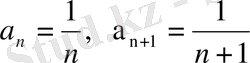 , олай болса,
, олай болса,
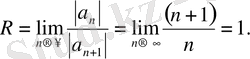
Қатардың жинақтылық интервалы: (-1; 1) .
Енді
 болғанда бұл жағдайды қосымша зерттейміз.
болғанда бұл жағдайды қосымша зерттейміз.
 болғанда
болғанда
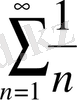 гормоникалық қатар шығады, ло жинақталмайды.
гормоникалық қатар шығады, ло жинақталмайды.
 болғанда
болғанда
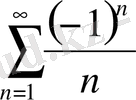 қатары Лейбниц теоремасы бойынша жинақталады. Сонымен
қатары Лейбниц теоремасы бойынша жинақталады. Сонымен
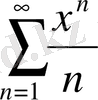 қатарының жинақталу жиыны (-1; +1) болатыны дәл осылай дәлелденеді.
қатарының жинақталу жиыны (-1; +1) болатыны дәл осылай дәлелденеді.
Тейлор қатары .
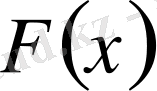 функциясы
функциясы
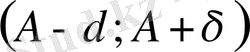 интервалында анықталып,
а
нүктесінде ақырсыз рет дифференциалдансын, яғни әр
интервалында анықталып,
а
нүктесінде ақырсыз рет дифференциалдансын, яғни әр
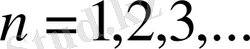 үшін бар болсын. Онда
үшін бар болсын. Онда
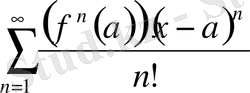 (1. 2. 4)
(1. 2. 4)
түріндегі дәрежелік қатар
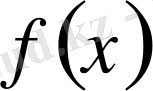 функциясын
а
нүктесіндегі Тейлор қатары деп аталады.
функциясын
а
нүктесіндегі Тейлор қатары деп аталады.
Ақырсыз рет дифференциалданатын функцияны Тейлор қатарының қосындысы ретінде бейнелеу сол функцияны Тейлор қатарына жіктеу деп аталады. Бұл жіктеу жалғыз болады.
Қатар жинақталуының анықтамасы мен (1. 2. 4) теңдіктен:
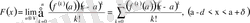 (1. 2. 5)
(1. 2. 5)
теңдігі орындалу үшін
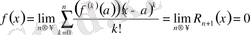
теңдігі орындалуы қажетті және жеткілікті. Мұндағы
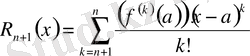
Тейлор мүшесінің қалдық мүшесі деп аталады. Егер
 деп алсақ, онда (1. 2. 5) формуладан Маклорен қатары шығады:
деп алсақ, онда (1. 2. 5) формуладан Маклорен қатары шығады:
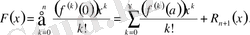
Теорема.
Айталық
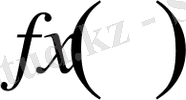 функциясы және оның барлық туындылары
функциясы және оның барлық туындылары
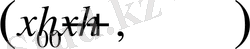 аралығында шенелген болса, яғни барлық
аралығында шенелген болса, яғни барлық
 және
және
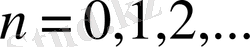 үшін қандай да бір
үшін қандай да бір
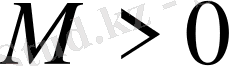 саны табылып
саны табылып
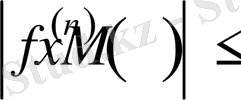 (1. 2. 6)
(1. 2. 6)
теңсіздігі орындалса, онда
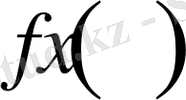 функциясы
функциясы
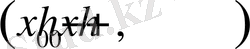 аралығында Тейлор қатарына жинақталады.
аралығында Тейлор қатарына жинақталады.
Егер
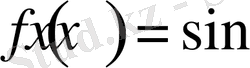 болса, онда
болса, онда
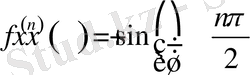 болады. Демек, барлық
болады. Демек, барлық
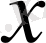 нақты сандары үшін
нақты сандары үшін
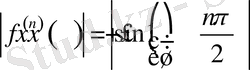
теңсіздігі орынды болады. Онда 2. 1-теоремаға сәйкес
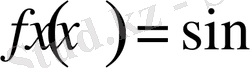 функциясы Тейлор қатарына жинақталады және келесі түрде жазылады.
функциясы Тейлор қатарына жинақталады және келесі түрде жазылады.
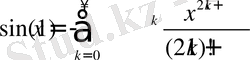
Сәйкесінше,
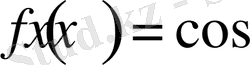 функциясын да дәл осы жолмен Тейлор формуласына жіктелетінін көрсетуге болады және ол келесі түрде жазылады
функциясын да дәл осы жолмен Тейлор формуласына жіктелетінін көрсетуге болады және ол келесі түрде жазылады
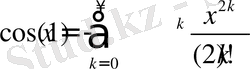
Жоғарыдағы (1. 2. 2) формуланы және 2. 1-теореманы қолдана отырып көрсеткіштік функцияның Тейлор қатарына жіктелуін анықтай аламыз:
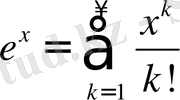
Гамма-функция және оның қасиеттері.
Гамма функция
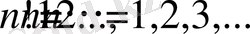
түріндегі факториалдың нақты сандар, теріс сандар, тіпті комплекс сандар облысындағы жалпыламасы болып табылады. Бұл жалпылау келесі интеграл арқылы өрнектеледі
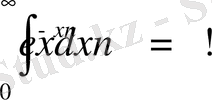 .
.
Берілген
 үшін
үшін
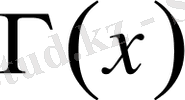 функциясы келесі түрдегі екінші текті Эйлер интегралы арқылы анықталады
функциясы келесі түрдегі екінші текті Эйлер интегралы арқылы анықталады
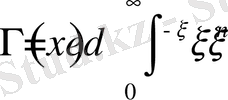 .
.
Жоғарыдағы гамма-функцияның формуласынан дербес жағдайда
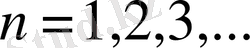 үшін
үшін
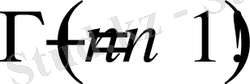 орындалатынын байқау қиын емес және осыдан барлық оң
орындалатынын байқау қиын емес және осыдан барлық оң
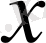 үшін
үшін
 .
.
Теріс сандар облысында гамма-функцияны оның оң мәнін пайдаланып есептеуді толықтыру формуласы деп атаймыз және келесі түрде өрнектейміз
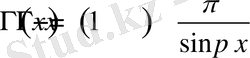 .
.
Келтіру формуласы. Егер
 саны беріліп, мұндағы
саны беріліп, мұндағы
 - бүтін сан, ал
- бүтін сан, ал
 болса, онда
болса, онда
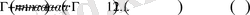 .
.
Бұл формуланы келесі түрде де жазуға болады:
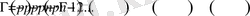 ,
,
егер
 болса.
болса.
Гамма-функцияның асимптотикалық көрінісі.
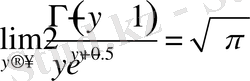 .
.
Гамма-функцияның кейбір қасиеттері.
1.
 ;
;
2.
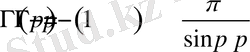 ;
;
3.
 ;
;
4.
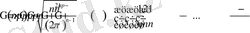 ;
;
Бета-функция және оның қасиеттері.
Бета-функция анықтамасы.
Бета-функция немесе Эйлердің бірінші текті интегралы деп келесі өрнекпен анықталған функцияны айтамыз:
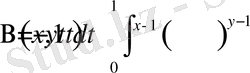 .
.
Бета-функцияның қасиеттері.
1. Бета-функция айнымалыларына қарағанда симметриялы, яғни
 .
.
2. Бета-функцияы гамма-функция арқылы жазуға болады:
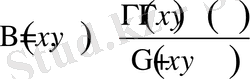 ,
,
мұндағы
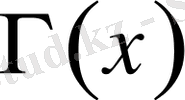 - гамма-функция.
- гамма-функция.
3.
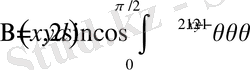 .
.
4.
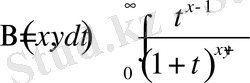 .
.
5.
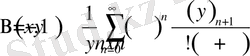 ,
,
мұндағы
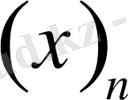 - келесі теңдікпен анықталады
- келесі теңдікпен анықталады
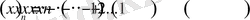 .
.
Миттаг-Леффлер функциясы және оның қасиеттері.
Қандай да бір
 нақты саны үшін
нақты саны үшін
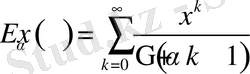
қатарымен анықталған функцияны Миттаг-Леффлердің бір параметрлі функциясы деп атайды.
Миттаг-Леффлер функциясы
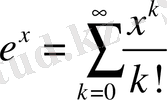
экспоненциалдық функциясының жалпыламасының бірі болып табылады. Яғни,
 болғанда
болғанда
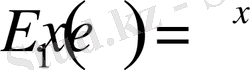 болады. Сондай-ақ
болады. Сондай-ақ
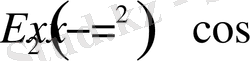 ,
,

болатынын да байқау қиын емес.
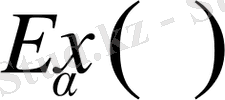 функциясының қасиеттері.
функциясының қасиеттері.
1)
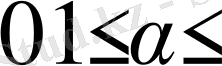 болса, онда
болса, онда
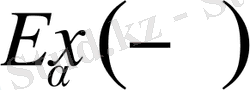 функциясы оң және монотонды, яғни
функциясы оң және монотонды, яғни
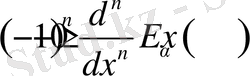 ,
,
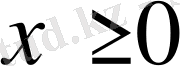 ,
,
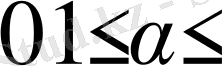 ,
,
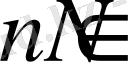 .
.
2)
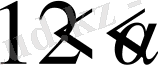 болса
болса
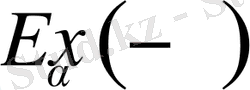 функциясының түбірлерінің саны тақ болады, онда
функциясының түбірлерінің саны тақ болады, онда
 функциясы шексіз түбірге ие болады.
функциясы шексіз түбірге ие болады.
3)
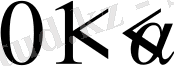 және
және
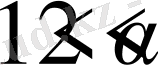 болса, онда келесі асимптотикалық жіктелу орынды:
болса, онда келесі асимптотикалық жіктелу орынды:
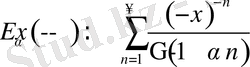 ,
,
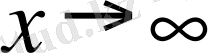 ,
,
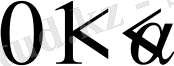 ,
,
 .
.
Екі параметрлі Миттаг-Леффлер функциясы.
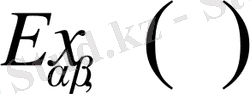 Миттаг-Леффлер екі параметрлі функциясы бір параметрлі функциядағы гамма-функция аргументіндегі 1 санын
Миттаг-Леффлер екі параметрлі функциясы бір параметрлі функциядағы гамма-функция аргументіндегі 1 санын
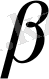 параметрімен ауыстырудан келіп шығады:
параметрімен ауыстырудан келіп шығады:
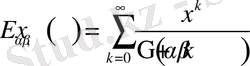 .
.
Екі параметрлі Миттаг-Леффлер функциясы үшін келесі функционалдық байланыстар орынды:
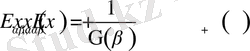 ,
,
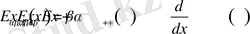 ,
,

Дербес жағдайлар:
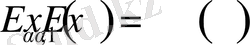 ,
,
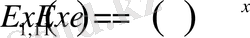 ,
,
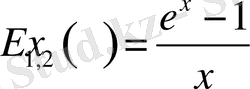 ,
,
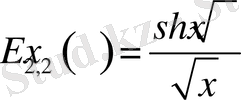 ,
,
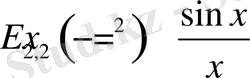 .
.
Тригонометриялық және гиперболалық функциялардың кейбір дифференциалдық теңдеулерді шешуде қолданылуы.
Бізге 1. 2. -параграфтан белгілі синустың дәрежелік қатар көрінісін алайық:
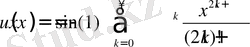
және оны бір рет дифференциалдайық. Сонда
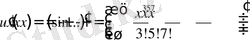

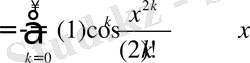 .
.
Енді косинустың қатар көрінісінен дифференциал алайық. Косинусты бір рет дифференциалдау жоғарыдағы өрнекті есепке алсақ синустан алынған екінші ретті дифференциалға тең. Яғни
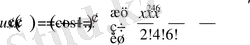

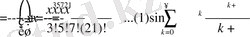 .
.
Демек
 .
.
Егер
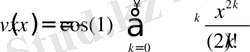
деп алсақ, онда
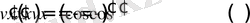 .
.
Айталық бізге
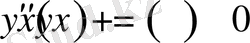 (1. 2. 14)
(1. 2. 14)
түріндегі екінші ретті дифференциалдық теңдеуді шешу қажет болсын.
Жоғарыдағы косинус пен синустың екінші ретті дифференциалын пайдалана отырып
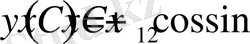 (1. 2. 15)
(1. 2. 15)
функциясы (1. 2. 14) дифференциалдық теңдеуін қанағаттандыратынын байқаймыз. Онда (1. 2. 15) функциясы (1. 2. 14) дифференциалдық теңдеуінің жалпы шешімі болады. Есептерді осы түрдегі операторлық әдіспен шешу жайлы [23] еңбекте кеңірек айтылған.
2. Жалпыланған тригонометриялық, гиперболалық функциялар және олардың кейбір дифференциалдық теңдеулерді шешуде қолданылуы.
2. 1. Жалпыланған тригонометриялық функциялардың анықтамасы.
Бізге математикалық талдау пәнінен тригонометриялық функциялардың төмендегідей қатарға жіктелетіні белгілі [22, 24] :
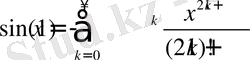
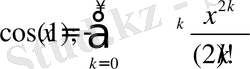
Енді біз осы функциялардың жалпы түрін анықтайық.
0≤α<1 болсын. Онда жалпыланған синусты төмендегідей түрде анықтаймыз:
 (2. 1. 1)
(2. 1. 1)
Егер α=0, ⇒


Жалпыланған синусқа сәйкес жалпыланған косинустың анықтамасын береміз:
 (2. 1. 2)
(2. 1. 2)
Егер α=0, ⇒
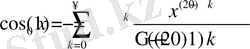
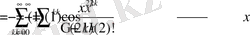
Жалпыланған тригонометриялық функцияларды Миттаг-Леффлер функциясы түріне келтіру.
Жалпыланған тригонометриялық функцияларды Миттаг-Леффлер түріне келтіреміз. Ал, Миттаг-Леффлер функциясының барлық қасиеттері [1-2] жұмыста көрсетілген.
Айталық
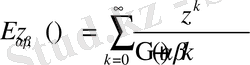 - Миттаг-Леффлер түріндегі функция болсын.
- Миттаг-Леффлер түріндегі функция болсын.
Енді біз жалпыланған тригонометриялық функцияларды Миттаг-Леффлер функциясы түріне келтіреміз.
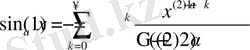

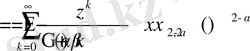
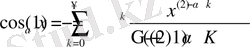

 ;
;
Жалпыланған тригонометриялық функциялардың туындысы және кейбір дифференциалдық теңдеулермен байланысы.
Енді жалпыланған тригонометриялық функциялардың бүтін және бөлшек ретті туындыларын қарастырайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz