Мектепте алгебралық және геометриялық материалдарды қабылдау мен меңгеру ерекшеліктері

Кіріспе

ДӘРІСТЕР КЕШЕНІ
Тақырып 1. Мектепте алгебралық және геометриялық материалдарды қабылдау мен меңгеру ерекшеліктері
Дәріс мақсаты: студенттерді оқу материалдарын қабылдау мен меңгеру ерекшеліктерімен таныстыру.
Тақырыптың сұрақтары:
- жасөспірімдердің даму ерекшеліетері мен соған орай алгебраны оқытудың өзгешеліктері
- алгебраны пән ретінде оқытудың ерекшеліктері
- геометриялық түсініктердің шынайы ерекшеліктері
- геометриялық кеңістікті қабылдау мен меңгеру
- алгебраның дамуы мен оны оқытуда қолдану
- алгебра курсының мазмұны мен міндеттері
- баламалы бағдарламалардың ерекшеліктері
Тақырыптың қысқаша мазмұны (тезис):
Жас өспірімдердің оқу материалдарын қабылдау мен меңгеруге ықпал ететін келесі ерекшеліктерін ажыратады: абстрактілі ойлау рөлінің артуы, ойлау үрдісінің жақсаруы, танымдық қызығушылықтарының артуы.
Алгебраны пән ретінде оқытудың ерекшеліктері мыналарды қамтиды: мазмұнның абст-рактілігі; терминология және символика; материалды алгоритмдеу үйлестіру қажеттілігі мен стандартты емес ойлау қажеттілігі, материалды баяндау сипатын талдау; оқушылардың жас ерекшеліктерінің жеткілікті ескерілмеуі мен түрткінің жоқтығы Алгебраны оқытуда нақты-индуктив¬ный әдіс маңызды рөл атқауы тиіс.
Күнделікті өмірде және оқыту үрдісінде оқушыларға кездесетін перцептивтік және геометриялық кеністіктің ерекшеліктері үйрету сипатына сүйенуі керек. Баланың дамуы мен оқу үрдісінің үйлесімділігі оның тәжірибесін, психикалық ұйымдастыру және геометриялық материалды қабылдау ерекшеліктерін есепке алудан тұрады
Өзін-өзі бақылау тапсырмалары:
1. Қай материал, алгебралық немесе геометриялық, сіз үшін меңгеру үшін қиынырақ болып табылады? Мұны қалай түсіндіресіз?
2. Алгебрада, геометрияда сізді өзіне не тартады?
3. Ұйғарым ақиқат па: егер а > b, онда 2а > 2b?
4. Останкино телебағанасы биіктігі 530 м, 30 000 тонна тартады. Оның дәл көшірмесінің биіктігі 53 см болса, онда салмағы қанша болады?
Әдебиеттер тізімі: 1-4
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану қажет.
Тақырып 2-3. Сандар жүйелері
Дәріс мақсаты: студенттерді берілген ұғымды оқып үйренудің түрлі жолдарымен және оқулықтардағы баяндаулармен таныстыру, сан жиындарын кеңейту туралы мағлұматтарды жалпылау мен жүйелеу әдістемесін көрсету.
Тақырыптың сұрақтары:
- нақты санның даму тарихы
- санды анықтаудың және сандар жиынын кеңейтудің жолдары. Сандар желісін оқудың мақсаттары.
- негізгі мектепте алгебра курсында сандар жиынын кеңейтудің әдістемелік ерекшеліктері
- 5 сыныпта бөлшек ұғымын енгізу әдістемесі
- «иррационал сан» ұғымын енгізу әдістемесі
- «комплекс сан» ұғымын енгізу әдістемесі
Тақырыптың қысқаша мазмұны (тезис):
Сандар жиынын кеңейту перманенттілік ұстанымын жүзеге асыру арқылы жүреді. Оқулықтарда натурал сандар жиынынан бастап, рацинал сандар жиынына дейінгі кеңейтулердің әртүрлі бірізділігі іске асырылады.
Иррационал сандар кесінділердің өлшеусіздігін бейнелейді. Рационал сандардың иррационал сандармен толықтырылуы нақты сандар жиынынң үзіліссіздігіне әкеледі.
Комплекс сандарды алгебралық және геометриялық амалдарды үйлестіру негізінде енгізуге болады.
Математикалық талдау элементтерін оқып үйренудің мәдени, дүниетанымдық, қолданбалық маңызы бар. Дәреже ұғымын қарастырғанда нақты санды анықтаудың түрлі жолдарын қарастыру, оқушыларды қысқаша комплекс сандармен таныстыру пайдалы.
Өзін-өзі бақылау тапсырмалары:
1. Нақты санның қандай анықтамасын білесіз?
2. Неге нөлге бөлуге болмайды?
3.Бөлшектерді оқытудың қандай бірізділігін қалайсыз: ондық бөлшектерді жай бөлшектерден кейін немесе керісінше? Әр жағдайдың артықшылықтары мен кемшіліктерін байқаңыз.
4. Нақты сандар жиынында рационал сандар жиынына қарағанда қандай жаңа қасиет пайда болады?
5. Түбір астындағы 3 санының рационал сан болмайтынын дәлелдеңіз.
6. Рационал санды өрнектейтін шексіз ондық бөлшек неге периодты болады?
7. Оқушылар иррационал санды қалай сипаттайды? Неге?
8. Квадраты 2-ге тең рационал санның болмауы туралы теореманы дәлелдеңіз.
9. Иррационал санды енгізу әдістемесі.
10. Нақты сандарды жіктеу.

Пән: Педагогика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

2 ТАРАУ. ДӘРІСТЕР КЕШЕНІ
Тақырып 1. Мектепте алгебралық және геометриялық материалдарды қабылдау мен
меңгеру ерекшеліктері
Дәріс мақсаты: студенттерді оқу материалдарын қабылдау мен меңгеру
ерекшеліктерімен таныстыру.
Тақырыптың сұрақтары:
- жасөспірімдердің даму ерекшеліетері мен соған орай алгебраны оқытудың
өзгешеліктері
- алгебраны пән ретінде оқытудың ерекшеліктері
- геометриялық түсініктердің шынайы ерекшеліктері
- геометриялық кеңістікті қабылдау мен меңгеру
- алгебраның дамуы мен оны оқытуда қолдану
- алгебра курсының мазмұны мен міндеттері
- баламалы бағдарламалардың ерекшеліктері
Тақырыптың қысқаша мазмұны (тезис):
Жас өспірімдердің оқу материалдарын қабылдау мен меңгеруге ықпал
ететін келесі ерекшеліктерін ажыратады: абстрактілі ойлау рөлінің артуы,
ойлау үрдісінің жақсаруы, танымдық қызығушылықтарының артуы.
Алгебраны пән ретінде оқытудың ерекшеліктері мыналарды қамтиды: мазмұнның
абстрактілігі; терминология және символика; материалды алгоритмдеу
үйлестіру қажеттілігі мен стандартты емес ойлау қажеттілігі, материалды
баяндау сипатын талдау; оқушылардың жас ерекшеліктерінің жеткілікті
ескерілмеуі мен түрткінің жоқтығы Алгебраны оқытуда нақты-индуктивный әдіс
маңызды рөл атқауы тиіс.
Күнделікті өмірде және оқыту үрдісінде оқушыларға кездесетін перцептивтік
және геометриялық кеністіктің ерекшеліктері үйрету сипатына сүйенуі керек.
Баланың дамуы мен оқу үрдісінің үйлесімділігі оның тәжірибесін, психикалық
ұйымдастыру және геометриялық материалды қабылдау ерекшеліктерін есепке
алудан тұрады
Өзін-өзі бақылау тапсырмалары:
1. Қай материал, алгебралық немесе геометриялық, сіз үшін меңгеру үшін
қиынырақ болып табылады? Мұны қалай түсіндіресіз?
2. Алгебрада, геометрияда сізді өзіне не тартады?
3. Ұйғарым ақиқат па: егер а b, онда 2а 2b?
4. Останкино телебағанасы биіктігі 530 м, 30 000 тонна тартады. Оның дәл
көшірмесінің биіктігі 53 см болса, онда салмағы қанша болады?
Әдебиеттер тізімі: 1-4
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған
жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану
қажет.
Тақырып 2-3. Сандар жүйелері
Дәріс мақсаты: студенттерді берілген ұғымды оқып үйренудің түрлі
жолдарымен және оқулықтардағы баяндаулармен таныстыру, сан жиындарын
кеңейту туралы мағлұматтарды жалпылау мен жүйелеу әдістемесін көрсету.
Тақырыптың сұрақтары:
- нақты санның даму тарихы
- санды анықтаудың және сандар жиынын кеңейтудің жолдары. Сандар желісін
оқудың мақсаттары.
- негізгі мектепте алгебра курсында сандар жиынын кеңейтудің әдістемелік
ерекшеліктері
- 5 сыныпта бөлшек ұғымын енгізу әдістемесі
- иррационал сан ұғымын енгізу әдістемесі
- комплекс сан ұғымын енгізу әдістемесі
Тақырыптың қысқаша мазмұны (тезис):
Сандар жиынын кеңейту перманенттілік ұстанымын жүзеге асыру арқылы
жүреді. Оқулықтарда натурал сандар жиынынан бастап, рацинал сандар жиынына
дейінгі кеңейтулердің әртүрлі бірізділігі іске асырылады.
Иррационал сандар кесінділердің өлшеусіздігін бейнелейді. Рационал
сандардың иррационал сандармен толықтырылуы нақты сандар жиынынң
үзіліссіздігіне әкеледі.
Комплекс сандарды алгебралық және геометриялық амалдарды үйлестіру
негізінде енгізуге болады.
Математикалық талдау элементтерін оқып үйренудің мәдени, дүниетанымдық,
қолданбалық маңызы бар. Дәреже ұғымын қарастырғанда нақты санды анықтаудың
түрлі жолдарын қарастыру, оқушыларды қысқаша комплекс сандармен таныстыру
пайдалы.
Өзін-өзі бақылау тапсырмалары:
1. Нақты санның қандай анықтамасын білесіз?
2. Неге нөлге бөлуге болмайды?
3.Бөлшектерді оқытудың қандай бірізділігін қалайсыз: ондық бөлшектерді жай
бөлшектерден кейін немесе керісінше? Әр жағдайдың артықшылықтары мен
кемшіліктерін байқаңыз.
4. Нақты сандар жиынында рационал сандар жиынына қарағанда қандай жаңа
қасиет пайда болады?
5. Түбір астындағы 3 санының рационал сан болмайтынын дәлелдеңіз.
6. Рационал санды өрнектейтін шексіз ондық бөлшек неге периодты болады?
7. Оқушылар иррационал санды қалай сипаттайды? Неге?
8. Квадраты 2-ге тең рационал санның болмауы туралы теореманы дәлелдеңіз.
9. Иррационал санды енгізу әдістемесі.
10. Нақты сандарды жіктеу.
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған
жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану
қажет.
Тақырып 4. Жуықтап есептеулер және оларға амалдар қолдану.
Дәріс мақсаты: студенттерді жуықтап есептеулерді оқып үйренудің түрлі
жолдарымен және оқулықтардағы баяндаулармен таныстыру, мектепте жуықтап
есептеулерді оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- жуықтап есептеулердің маңызы.
- жуықтап есептеулердің енгізі әдістері.
- жуықтап есептеулердің қолданбалық мәнісі.
- жуықтап есептеулер теориясының негізгі ұғымдарын қалыптастыру әдістемесі.
- жуықтап есептеулер амалдары.
Тақырыптың қысқаша мазмұны (тезис):
Физикада және техникада жуықтап есептеулер қолдану қателіктер
теориясының тура және кері есептерімен тығыз байланысты.
Қателіктер теориясының бұл есептері жуықтап есептеулер мазмұндық-
әдістемелік желісінің әрі қарай дамыту ретінде қарастырылады, себебі
оқушылар негізіг мектепте жуықтап сандарға арифметикалық амалдар қолдану
туралы түсініктер алады. Сонымен қатар, физика курсында зертханалық
жұмыс қарастырылған, онда олар приборлардан эксперименталдық деректерді ала
алады, жуық сандарға қарапайым ережелерді қолдана отырып, алған нәтижелерін
салыстырады.
Бейіндік мектептерде оқушылардың қателіктер теориясының элементтері
туралы түсініктерді кеңейткен жөн, атап айтқанда жуық санның абсолютті және
салыстырмалы шектік қателіктері, ақиқат ондық таңбалар ұғымдарын енгізу
керек; маңызды практикалық мәні бар қателіктер теориясының тура және кері
есептерімен таныстыру, көп айнымалы жағдайына есепті жалпылау қажет.
Өзін-өзі бақылау тапсырмалары:
1. Жуықтап есептеулерді мектеп курсына енгізу туралы тарихи мағлұматтардан
мысал келтіріңіз.
2. Негізгі ұғымдар мен жуық сандарға амалдар қолдану ережелерін енгізу
әдістемесін сипаттаңыз.
3. Жуық сандарға арифметикалық амалдар қолдануға 2 – 3 мысал келтіріңіз.
4. Ппрактикалық мазмұны жуық деректерден тұратын 2 – 3 есепті шешуге мысал
келтіріңіз.
5. Шекаралық тәсіл бойынша жуық сандарға амалдар қолдану туралы негізгі
теоремаларды атаңыз.
6. Негізгі мектепте шекаралық тәсіл бойынша амалдар қолдану ережелері
арқылы өрнектерді есептеуге мысал келтіріңіз.
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: 197273 оқу жылына дейінгі 7 сынып бағдарламасында
Жуықтап есептеулер тақырыбы бөлек қарастырылды. Қазіргі кездегі жаңа
бағдарламаға сәйкес бұл тақырыптың сұрақтары бүкіл мектеп математикасында
астарласып жатыр. Теңсіздіктер мен оларды жуықтап есептеулерге қолдану
және Жуықтап есептеулер тақырыптарын басты назарда ұстаған жөн.
Тақырып 5. Тепе-тең түрлендірулер.
Дәріс мақсаты: студенттерді тепе-тең түрлендірулерді оқып үйренудің түрлі
жолдарымен және оқулықтардағы баяндаулармен таныстыру, мектепте осы желіні
оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- ММК тепе-тең түрлендірулер желісі және оның басқа желілермен байланысы.
- түрлендірулердің негізгі түрлері және оларды оқудың кезеңдері.
- тапсырмалар жүйесін құру ерекшеліктері.
- тепе-теңдіктерді дәлелдеу.
- теңсіздіктерді түрлендіруді оқып үйренудің ерекшеліктері.
- Квадрат түбірі бар өрнектерді теп-тең түрлендіру тақырыбын оқып
үйренудің ерекшеліктері.
Тақырыптың қысқаша мазмұны (тезис):
Тепе-тең түрлендірулер алгебра курсында бір өрнекті оған тепе-тең
болатын екінші бір өрнекпен алмастыру ретінде қарастырылады.
Формальды тұрғыдан қарастырғанда егер екі өрнек бірі-бірінен формальды
түрлендіру арқылы алынса, Функциональдық тұрғыдан қарастырғанда егер екі
өрнек олардың құрамына кіретін әріптердің кезкелген жүйелерінде бірдей
сандық мәндерді қабылдаса, онда тепе-тең.
Тепе-тең түрлендірулер алгебра курсының барлық желілерімен
байланысты.
Тепе-тең түрлендірулер желсіні оқып үйрену төрт кезеңнен тұрады:
- кіріспе (5—6 сынптар);
- бірінші, онда жіктелмеген түрлендірулер жүйесі пайдаланылады (7 сынптың
басы);
- екінші, бұл үрдісте түрлендірулердің нақты түрлері ажыратылады (8—9
сыныптар);
- үшінші, тұтас түрлендірулер жүйесі ұйымдастырады (10—11 сыныптар).
Өзін-өзі бақылау тапсырмалары:
1. Математикалы өрнек дегеніміз не? Мысал келтіріңіз. ч
2. Тепе-тең түрлендірулер туралы не білесіз?
3. Теңдікті белгілеу үшін мына = таңбаны кім және қашан енгізді?
4. Теңдіктер тепе-тең бола ма: 3 + 2 = 5, , , ?
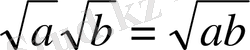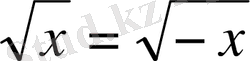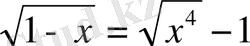5 Пайымдаулардағы қателіктерді табыңыз: 4 : 4 = 5 : 5, 4× (1 : 1) = 5×(1
: 1), 4 = 5.
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: Тепе-тең түрлендірулерді оқыту әдістемесіне қатысты
сұрақтар 1-3 әдебиеттерде келтірілген. Оқулықтар мен журналдарда да
мәліметтер жинау қажет. Қолданыстағы бағдарлама бойынша өрнектерге амалдар
қолдану емес, өрнектерді тепе-тең түрлендірулер оқылады. Осыған байланысты
оқып үйрену әдістемесі де өзгереді.
Тақырып 6-8. Мектеп математикасы курсындағы функциялық желі.
Дәріс мақсаты: студенттерді функция ұғымы мен оны оқып үйренудің түрлі
жолдары және жаңа буын оқулықтарындағы баяндаулармен таныстыру, мектепте
функциялық желіні оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- функцияның даму тарихынан
- негізгі мектеп функцияны оқып үйренудің мақсаттары
- функция ұғымының әртүрлі түсініктемелері
- функция ұғымын қалыптастыру
- функциялық-графиктік түсініктер негізінде пәнішілік байланыстарды жүзеге
асыру
- функцияны оқуда өмірмен және пәнаралық байланыстарды жүзеге асыру
- оқушылардың когнитивтік стилін есепке ала отырып функцияны оқыту
- мектепте қарапайым функцияларды оқып үйрену әдістемесі
- мектепте і тригонометриялық , көрсеткішітік және логарифмдік
функцияларды оқып үйрену әдістемесі
Тақырыптың қысқаша мазмұны (тезис):
Функцияның жалпымәдени, дүниетанымдық мәні бар. Оны оқып үйрену
оқушыларды жалпыға ортақ байланыс, үзіліссіздік, шексіздік, жуықтау
(интерполяция) идеяларымен таныстырады.
Функцияны оқып үйрену әр түрлі нысандардың өзгерулері арасындағы
байланыстарды көруге жауап беретін функциялық ойлауды дамытуға септігін
тигізеді.
Функция ұғымын баяндауды екіге бөлуге болады: айнымалы шамалар
ұғымына сүйенетін классикалық және теориялық-жиындық негіздегі қазіргі
кездегі баяндаулар.
Мектепте функция ұғымын оқып үйрену алты деңгейден тұрады: 1-ші
кіріспе (бастауыш мектеп); 2-ші кіріспе (5 - 6 сыныптар); 3-ші негізгі,
мұнда функция туралы жалпы түсініктер және оның қасиеттері, берілу
тәсілдерін қалыптастыру көзделеді (7—9 сыныптар); 4-6-ші жоғары сыныптарда
іске асады.
Функцияны оқып үйренуді оқушылардың когнитивтік стильдерін есепке
ала отырып жүргізген тиімді.
Өзін-өзі бақылау тапсырмалары:
1.Сәйкестік, функция, бейнелеу, қатынас, сандар функциясы ұғымдары
арасындағы қатынастарды Эйлер дөңгелектері арқылы кескіндеңіз.
2. Мұғалім графиктің түрлі формалары туралы айта келіп, параболаны салды.
Оқушы бірден оның квадраттық функцияның графигі екенін айтты. Оныкі дұрыс
па?
3. Функция идеясын дамытуға атсалысқан математиктардың есімдерін атаңыз.
4. Алғашында функцияны баяндау қандай сипатта (геометриялық немесе
аналитикалық) болды?
5. Функция идеясының пайда болуын қай кезге жатқызады? Оның авторы болып
кім есептеледі.
6. Функциялар тең бола ма: және .
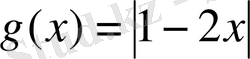7. 6 сыныпта функция ұғымын енгізу ерекшеліктерін беретін мысалдар
келтіріңіз.
8. Функциялық кіріспеге қатысты графикпен берілген тапсырмаларға мысалдар
келтіріңіз.
9. Функциялық ойлауды дамытуға септік ететін геометриялық сипаттағы
сұрақтар мен жаттығулар жүйелеріне мысал келтіріңіз.
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған
жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану
қажет.
Тақырып 9-11. Мектеп курсында теңдеулер мен теңсіздіктер желісі.
Дәріс мақсаты: студенттерді теңдеу, теңсіздік ұғымдарының түрлі
анықтамалары мен олардың кейбір түрленрін енгізу ерекшеліктерімен, оларды
шешу әдістері, оқып үйренудің түрлі кезеңдері, жолдары және жаңа буын
оқулықтарындағы баяндаулармен таныстыру, мектепте осы желіні оқып үйрену
әдістемесін көрсету.
Тақырыптың сұрақтары:
- математика курсындағы теңдеулер мен теңсіздіктер желісінің мазмұны мен
рөлі
- теңдеулер мен теңсіздіктер желісінің негізгі ұғымдары
- негізгі мектепте теңдеулер мен теңсіздіктер желісін оқып үйренудің
әдістемелік ерекшеліктері
- ссептерді теңдеулер құру арқылы шығару
- мектептегі негізгі теңдеулер мен теңсіздіктер, олардың жүйелері
- теңдеулерді шешудің сандық әдістері
Тақырыптың қысқаша мазмұны (тезис):
Теңдеу ұғымының түрлі баяндаулары бар: белгісіз саны бар теңдік;
бір айнымалысы бар теңдік; екі функцияның теңдігі. Теңдеулер мектеп
қарастырылатын функциялардың түрлеріне бойынша жіктеледі.
Мектеп оқулықтарында пар-пар түрлендірулер теңдеулерді (теңсіздіктерді)
шешу барысында пара-парлық ұғымын енгізуге дейін (немесе кейін)
пайдаланылады.
Теңдеулер мен теңсіздіктерді шешу кезінде олардың тек бір жағын
түрлендіру, не екі жағын да бірдей өзгерту, не олардың қисындық құрылымын
өзгертетін түрлендірулер пайдаланылады.
Теңдеулер мен теңсіздіктерді шешу функцияның қасиеттерін зерделеумен
тығыз байланысты. Теңдеулер мен теңсіздіктерді шешудің графиктік әдісі мен
интервалдар әдісі функцияның қасиеттеріне сүйенеді.
Өзін-өзі бақылау тапсырмалары:
1. Мына жазулар теңдеу бола ма:

2. Теңдеулер мен теңсіздіктерді шешудің жалпы әдістерін атаңыз.
3. Теңдеулер пара-пар бола ма:
,
4. 2х 13 теңсіздігі lg (2х - 3) 1теңсіздігінен шыға ма?
Әдебиеттер тізімі: 1-4
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған
жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану
қажет.
Тақырып 12. Сан тізбектері. Шек және үзіліссіздік.
Дәріс мақсаты: студенттерді тізбек, шек, үзіліссіздік ұғымдары мен оларды
оқып үйренудің түрлі жолдары және жаңа буын оқулықтарындағы баяндаулармен
таныстыру, мектепте осы желіні оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- сан тізбегі ұғымы.
- сан тізбегінің шегі ұғымы.
- сан тізбегінің шегі туралы теоремалар.
- функцияның щегі мен үзіліссіздігін оқып үйрену әдістемесі.
Тақырыптың қысқаша мазмұны (тезис):
Нақты-индуктивтік амалдың қисынына сай тізбектің шегі мен функция
шегінің аймақтық анықтамаын енгізу қолайлы. Ол туынды ұғымының
анықтамасын ұтымды енгізуге көмектеседі.
Функцияның шегі тізбектің шегі сияқты математиканың іргелі ұғымына
жатады. Оларға математикалық және қолданбалық мәндерден басқа
мәдениқисындық маңыз тән, сондықтан олармен математиканы түрлі бейіндік
мектептерде оқушыларды таныстыру қажет болыа табылады. Осы материалды
мектепте оқып үйрену жоғары математика курстарында осы ұғымдарды меңгеру
үшін дайындық кезеңі ретінде қарастыру болып саналады.
Өзін-өзі бақылау тапсырмалары:
1. Сан тізбегінің шегі ұғымын енгізу әдістемесі.
2. Сан тізбегінің шегі туралы теоремаларды қолдану жаттығуларына 3-4 мысал
келтіріңіз.
3. Шектер теориясын қолдану арқылы шеңбердің ұзындығы мен дөңгелектің
ауданын оқып үйрену әдістемесі.
4. Сіздіңше, тізбек пен функция шектерінің қай анықтамасы мектепте оқып
үйренуге ыңғайлы?
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: Сан тізбегі мен оның шегі ұғымына қатысты сұрақтар
алгебар мен элементарлық функциялар курстары ғана емес, геометрия курсында
да қарастырылады. Тізбектің шегі алгебра мен талдау курсында 10 сыныпта
оқытылады.
Тақырып 13. Туынды мен оның қолданысы.
Дәріс мақсаты: студенттерді туынды ұғымын оқып үйренудің түрлі жолдарымен
және оқулықтардағы баяндаулармен таныстыру, мектепте осы мазмұдық-
әдістемелік желіні оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- туынды ұғымын енгізу әдістемесі.
- туынды және дифференциал ұғымдарын енгізу туралы.
- функцияларды дифференциалдау теоремаларын оқып үйрену әдістемесі.
- функцияны зерттеуге туындыны қолдану оқып үйрену әдістемесі.
- есептер шығаруға туындыны қолдану.
Тақырыптың қысқаша мазмұны (тезис):
Функцияның туындысы мен оның қолдансын оқып үйрену: математиканың
іргелі ұғымдарының бірін таныстыруға; есептерді шешудің жаңа әдісін
енгізуге (үлгілерді зерттеудің жаңа әдісі); математиканың қолданбалық
мәнісін көрсету; пәнаралық байланыстарды жүзеге асыру; функциялық
білімдерді жүйелеуге бағытталған.
Бөлімнің негізгі мазмұны: туынды ұғымы, дифференциалдау техникасы,
функцияны зерттеуге және есептер шешуге туындыны қолдану.
Туынды арқылы функцияны зерттеуге арналған теориялық мтериалдарды
енгізудің түрлі нұсқалары бар: барлық ұйғарымдарды тұжырымдау және оларды
дәлелдеусіз келтіру; тероремаларды дәлелдеу сызбасын көрсету; Лагранж
формуласын дәлелдеусіз беру және оның негізінде басқа дәлелдеулерді
орындау.
Функцияны зерттеудің келесі сызбасы ұсынылады: анықталу облысы;
мәндерінің жиыны; жұп және тақтығы; өстермен қиылысуы; таңбатұрақтылық;
туынды және күмәнді нүктелер; бірсарындылығы мен зкстремумдары; доғалдығы
мен ойыстығы; иілу нүктелері; шексіздіктегі және үзіліс нүктелеріндегі
сипаты.
Өзін-өзі бақылау тапсырмалары:
1. Мектепте туындыны енгізу туралы трихи мәліметтерді келтіріңіз.
2. Туынды ұғымын енгізу әдістемесі.
3. Функцияларды дифференциалдау теоремаларын оқып үйрену әдістемесі.
4. Функцияны зерттеуге туындыны қолдану және графиктерін салуды оқып үйрену
әдістемесі.
5. Туынды арқылы функцияның экстремумдарын табуға арналған практикалық
мазмұнды есептер шығаруға 2-3 мысал келтіріңіз.
Әдебиеттер тізімі: 1-3
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін 1-3 әдебиеттерді таңдаған
жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік құралдарды да пайдалану
қажет.
Тақырып 14. Алғашқы функция мен интеграл.
Дәріс мақсаты: студенттерді алғашқы функция мен интеграл ұғымдарымен
таныстыру, оларды оқып үйренудің түрлі жолдарымен және оқулықтардағы
баяндаулармен таныстыру, мектепте осы мазмұдық-әдістемелік желіні оқып
үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- алғашқы функция мен интеграл ұғымдарын енгізу әдістемесі.
- интегралды аудандарды есептеуге қолдану
- интегралды көлемдерді есептеуге қолдану.
Тақырыптың қысқаша мазмұны (тезис):
Алғашқы функция дифференциалдауға кері амал ретінде енгізілуі
мүмкін. Анықталған интеграл ұғымын тарихи-ғылыми тәсіл қисынына сай
оқушылардың ауданның қасиеттері туралы білімдері, шеңбердің ұзындығы мен
дөңгелектің ауданын біртіндеп жуықтату әдісімен табу тәжірибесі негізінде
енгізу тиімді. Анықталмаған интеграл ұғымы оқулықты негізінде енгізіледі.
Өзін-өзі бақылау тапсырмалары:
1. Қисық сызықты трапецичяның ауданына және жылдамдығы бойынша жолды
анықтауға есептер шығару әдістемесі.
2. Анықталған интеграл ұғымын енгізу әдістемесі.
3. Ньютон-Лейбниц формулсын қорыту әдістемесі.
4. Дөңгелектің ауданын, пирамиданың көлемін қорытып шығару үшін интегралды
қолдану әдістемесі.
Әдебиеттер тізімі: 1-4
Әдістемелік нұсқаулар: Тереңірек қарастыру үшін ұғымдарды енгізудің бірнеше
жодарын таңдаған жөн. Оқулықтар мен оқу бғдарламаларын, әдістемелік
құралдарды да пайдалану қажет.
Тақырып 15. Мектеп курсындағы ықтималдық-статистикалық желі.
Дәріс мақсаты: студенттерді ықтималдар мен статистика теориясының
ұғымдарымен таныстыру, оларды оқып үйренудің түрлі жолдарымен және
оқулықтардағы баяндаулармен таныстыру, мектепте осы мазмұдық-әдістемелік
желіні оқып үйрену әдістемесін көрсету.
Тақырыптың сұрақтары:
- ықтималдар мен статистика теориясы элементтерін оқытудың негізгі
мақсаттары.
- ықтималдар мен статистика теориясының негізгі ұғымдары.
- негізі теоремаларды оқып үйрену әдістемесі.
- кездейсоқ шама ұғымын енгізу әдістемесі.
Тақырыптың қысқаша мазмұны (тезис):
Ықтималдар теориясы мен математикалық статистика элементтерін
мектепте оқытудың негізгі мақсаттарына нақты дүниенің құбылыстарының
стохастикалық үлгілерін құру арқылы оларды сипаттау және оқып үйрену құралы
ретінде осы ғылыммен таныстыру жатады.
Олардың негізгі ұғымдарын оқудың әдістемелік ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.