Параболалық типтес дифференциалдық теңдеулердің бастапқы және шеткі есептерін Грин функциясы әдісімен екі және үш өлшемді кеңістікте шешу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:
КІРІСПЕ
Табиғат құбылыстарын зерттегенде, физика және техника, химия және биология мәселелерін шешкенде, эволюциялық процесті анықтайтын шамалар арасындағы тәуелділік, көбіне шамалар мен олардың өзгеру жылдамдықтары арасындағы байланыс түрінде, яғни белгісіз функциялар мен туындыларын (дифференциалдарын) байланыстыратын теңдеу ретінде алынады. Белгісіз функция және оның туындыларын байланыстыратын мұндай теңдеулер дифференциалдық деп аталады.
Ізделінді функцияның ең жоғарғы туындысы (дифференциалы) теңдеудің реті деп аталады. Келтірілген екінші, үшінші мысалдардағы теңдеулер екінші ретті.
Теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыратын функция теңдеудің шешімі деп аталады.
Дифференциалдық дербес туындылы теңдеулер математикалық физикада кеңінен қарастырылады. Математикалық физика, әртүрлі физикалық процестермен тығыз байланысты. Физикалық процестердің характеристикасы белгілі бір теңдеу типіне сәйкес келеді. Әрбір типті зерттеп білу, қарастырылып отырған теңдеу типіне алып келетін физикалық есептерден басталады. Дифференциалдық теңдеулерге арналған есептерді шешуде көп қолданылатын әдістердің бірі Грин функциясы әдісі болып табылады. Оны 1830 жылға тиісті теорияны алғашқы рет ағылшын ғалымы Джордж Гриннің құрметіне атаған. Бұл әдіс, алдымен, қарастырылатын типтің кейбір арнайы есеп шешімін тауып, интеграл арқылы өрнектейді. Сонымен қатар, бұл әдіс электростатикада Пуассон теңдеуін шешуде, жылуөткізгіштік теңдеуін шешуде таптырмас әдіс.
Дифференциалдық теңдеулер есептеріне физика - техникалық көптеген үдерістер мәселелері келтірілетіні белгілі. Ғылыми тұрғыдан мұндай құбылыстарлы жүйелі зерттеу, дифференциалдық теңдеулердің бастапқы және шекаралық шарттарымен қойылған есептерінің шешімдерін таба білумен байланысты.
Бұл жұмыс үш бөлімде қарастырылады. Бастапқы және шеттік шартты есептер түсініктері, сызықтық кәдімгі дифференциалдық теңдеудің шеттік есебі қарастырылып, Грин функциясының бар болуы теоремасы зерттелген. Мысал арқылы Грин функциясы құрылып, біртекті емес теңдеудің шешімі құрылған.
Осы негізде парабола типтес дербес туындылы дифференциалдық теңдеудің шеттік есебі үшін Грин функциясы енгізіліп, есептің шешімі интегралдық түрде анықталған. Мұнда да алдымен біртекті есеп, сонан соң біртекті емес есеп шешімдері анықталып, олардың дифференциалдық қасиеттері түбегейлі зерттелген.
Грин функциясы айнымалыларды ажырату әдісімен құрылатыны көрсетіліп, нақтыланған.
Түзуде Коши есебінің Грин функциясы қалай құрылытыны жеке қарастырылып, Фурьенің интегралдық түрлендіруінің қолданысы ұсынылған. Әрі қарай жарты түзу есептерін шешу әдістері көрсетілген. Көрсетілген әдістердің қолданылуына мысалдар қарастырылған.
Үш өлшемді кеңістікте жылу таралуы есебі зерттеліп, Коши есебі шешімінің орнықтылығы тұжырымдалған.
Грин функциясы әдісі шексіз кеңістік немесе жарты кеңістік есептеріне қолданылатындары дәлелдеулерімен көрсетілген.
Дипломдық жұмыстың мақсаты: Бастапқы және шеттік есептерді шешу арқылы парабола типтес теңдеу есептерге Грин функциясы әдісін қолданып екі өлшемді, үш өлшемді кеңістікте есеп шешімін табу.
1 БАСТАПҚЫ ЖӘНЕ ШЕТТІК ШАРТТЫ ЕСЕПТЕР ТҮСІНІКТЕРІ
1. 1 ЖӘЙ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУ ЕСЕБІНІҢ ГРИН ФУНКЦИЯСЫ
Кіріспе бөлімнен бастап бастапқы есепті шешу үшін шеттік және шекаралық деп аталатын есептерге тоқталайық.
Мұндай есептерде ізделінді фунцияның мәнін шектелген кесіндінің бір емес екі нүктесін табу арқылы шешімді анықтайды. Бастапқы шартпен берілген есептермен қатар, шет нүктелеріндегі шарттарымен де қарастырылатын есептер жиі ұшырасады. Мысалы, массасы
 материалдық нүкте
материалдық нүкте
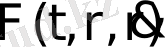 күшінің әсерімен қозғалысында
күшінің әсерімен қозғалысында
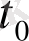 бастапқы сәтінде
бастапқы сәтінде
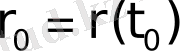 радиус-векторымен анықталатын нүктеде, ал
радиус-векторымен анықталатын нүктеде, ал
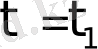
 сәтінде
сәтінде
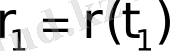 радиус-векторымен анықталатын нүктеге түсуі керектігінің қозғалыс заңын табу керек.
радиус-векторымен анықталатын нүктеге түсуі керектігінің қозғалыс заңын табу керек.
Есеп дифференциалдық теңдеуді
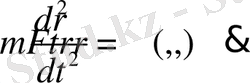
шеттік
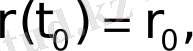
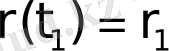 шарттарымен интегралдауға келтіріледі.
шарттарымен интегралдауға келтіріледі.
Бұл есебімізде былайша айтқанда жалғыз ғана шешімге ие еместігін байқадық, егерде сөз баллистикалық есеп туралы және жер кеңістігінің нүктесі туралы болса, онда дәл сол нүктеде дене траектория бойына түсуі мүмкін, сонымен қатар, өте үлкен бастапқы жылдамдықпен жер шарының бір немесе бірнеше айналуынан соң дәл сол нүктеге түсуі мүмкін. Сондай-ақ шеттік есепті орта арқылы өтетін жарық сәулесі деп қоюға болады, А нүктеден шығып В басқа нүктесіне түсетін бағытты табатын етіп қоюға болады.
Теңдеудің жалпы шешімі болса, есептің берілген шартты орындайтын шешімін табу үшін, шеттік шарттарды қолданып, тұрақтылардың мәндерін анықтаймыз.
Мұнда нақты шешім барлық уақытта бола бермеуі де және жалғыз болмауы да мүмкін.
Мысал 1.
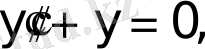
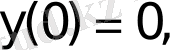
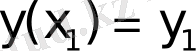 (1. 1. 1)
(1. 1. 1)
есебін қарастырайық.
(1. 1. 1) теңдеудің жалпы шешімі
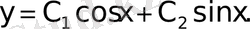
Бірінші шеттік шарт
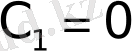 мәнінде орындалғандықтан, шешім
мәнінде орындалғандықтан, шешім
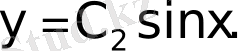
Егер
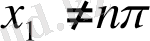
 - бүтін болса, екінші шарттан
- бүтін болса, екінші шарттан
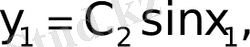
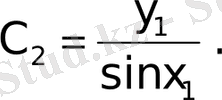
демек бұл жағдайда есептің жалғыз шешімі
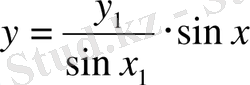
бар.
Егер
 және
және
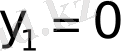 болса, онда барлық қисықтар
болса, онда барлық қисықтар
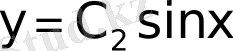 графикалық шеттік есеп шешімі болады.
графикалық шеттік есеп шешімі болады.
Егер
 және
және
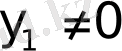 болса, онда есептің шешімі жоқ.
болса, онда есептің шешімі жоқ.
Екінші ретті сызықтық теңдеудің шеттік есебін қарастырайық
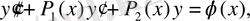 (1. 1. 2)
(1. 1. 2)
 (1. 1. 3)
(1. 1. 3)
сызықтық түрлендіру
нәтижесінде шеттік шарттар (1. 1. 3) нөлдік шарттарға
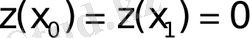 келтіріледі, теңдеудің (1. 1. 2) сызықтығы өзгермейді.
келтіріледі, теңдеудің (1. 1. 2) сызықтығы өзгермейді.
Теңдеуді (1. 1. 2)
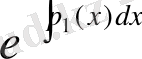 - ке көбейтіп, мына түрге келтіреміз
- ке көбейтіп, мына түрге келтіреміз
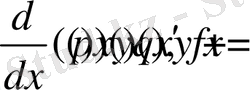 (1. 1. 4)
(1. 1. 4)
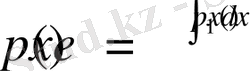 , сондықтан (1. 1. 4) шеттік есебін зерттеуді
, сондықтан (1. 1. 4) шеттік есебін зерттеуді
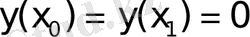 (1. 1. 5)
(1. 1. 5)
шеттік (1. 1. 2) (1. 1. 3) есебін зерттеумен алмастыра аламыз.
Шеттік есепті (1. 1. 4) - (1. 1. 5)
 нүктесінің төңірегінде
нүктесінің төңірегінде
 функциясы бірлік импульсті, яғни
функциясы бірлік импульсті, яғни
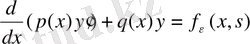 (1. 1. 6)
(1. 1. 6)
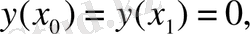
мұндағы
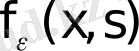 кесіндіде
кесіндіде
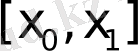 нөлге тең,
нөлге тең,
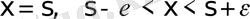
төңірегінде
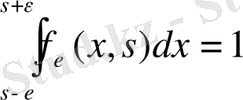
деп қарастырамыз. Бұл шеттік есептің үздіксіз шешімін
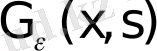 деп
деп
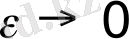 шекке көшеміз:
шекке көшеміз:
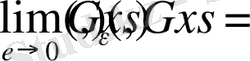 (1. 1. 7)
(1. 1. 7)
Функция
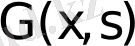 қарастырылып отырған шеттік есептің әсері немесе Грин функциясы деп аталады. Шеттік есептің (1. 1. 4) - (1. 1. 5) шешімі
қарастырылып отырған шеттік есептің әсері немесе Грин функциясы деп аталады. Шеттік есептің (1. 1. 4) - (1. 1. 5) шешімі
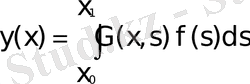 (1. 1. 8)
(1. 1. 8)
екендігіне, интегралдық қосындылар шегі арқылы көз жеткіземіз.
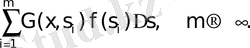
Грин функциясының қасиеттері:
1.
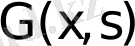 функциясы берілген
функциясы берілген
 мәнінде
мәнінде
 арқылы
арқылы
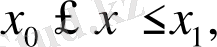
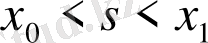 аралықтарында үздіксіз;
аралықтарында үздіксіз;
2.
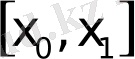 кесіндісінің
кесіндісінің
 нүктесінен басқа барлық нүктелерінде
нүктесінен басқа барлық нүктелерінде
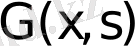 функциясы біртекті
функциясы біртекті
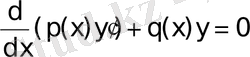
теңдеуінің шешімі;
3.
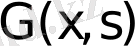 шекаралық шарттарды қанағаттандырады;
шекаралық шарттарды қанағаттандырады;
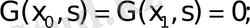
4.
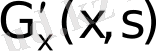 туындысы
туындысы
 нүктесінде үзілісті, секірісі
нүктесінде үзілісті, секірісі
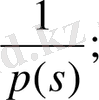
Шындығында
 нүктесі күтіп тұр.
нүктесі күтіп тұр.
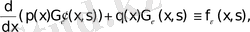
тепе-теңдігін
 көбейтіп,
көбейтіп,
 шетерінде интегралдаймыз.
шетерінде интегралдаймыз.
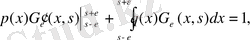 нүктесінде үзіліс
нүктесінде үзіліс
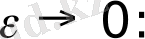
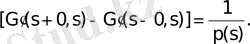
Анықтама.
Сонымен, (1. 1. 4) -(1. 1. 5) шеттік есептің Грин функциясы
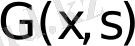 деп, жоғарыда аталған (1) - (4) қасиеттерін орындайтын функцияны айтады.
деп, жоғарыда аталған (1) - (4) қасиеттерін орындайтын функцияны айтады.
Теңдеудегі (1. 1. 4) тікелей қою жолымен
 (1. 1. 8)
(1. 1. 8)
функция есептің шешімі екендігіне көз жеткізіміз.
Шындығында,
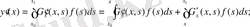
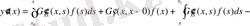
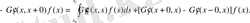
онда (1. 1. 8) -ді (1. 1. 4) теңдеуге қойып
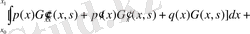
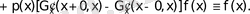
Грин функциясын құру әдісімен, оның бар болуының жеткілікті шартын көреміз. Теңдеудің
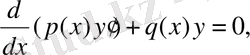 (1. 1. 9)
(1. 1. 9)
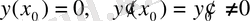
бастапқы шарттарын қанағаттандыратын
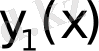 шешімін қарастырайық. Бұл шешім жалпы жағдайда екінші шеттік шартты
шешімін қарастырайық. Бұл шешім жалпы жағдайда екінші шеттік шартты
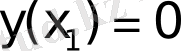 қанағаттандырмайды.
қанағаттандырмайды.
Шешімдер
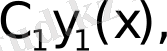
 - кезкелген тұрақты, шеттік шартты
- кезкелген тұрақты, шеттік шартты
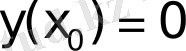 қанағаттандырады. Осы сияқты шеттік
қанағаттандырады. Осы сияқты шеттік
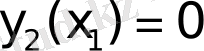 шартын қанағаттандыратын
шартын қанағаттандыратын
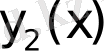 шешімі табылады; онда бұл шартты барлық
шешімі табылады; онда бұл шартты барлық
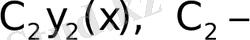 кез-келген тұрақты, шешімдері де орындайды.
кез-келген тұрақты, шешімдері де орындайды.
Грин функциясы
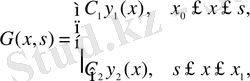
түрінде іздестіріліп, тұрақтылар
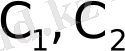 3) және 4) қасиеттердің орындалуынан табылады, яғни
3) және 4) қасиеттердің орындалуынан табылады, яғни
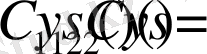 (1. 1. 10)
(1. 1. 10)
 x=s нүктесінде
x=s нүктесінде
 секіріс бар
секіріс бар
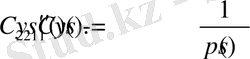 (1. 1. 11)
(1. 1. 11)
Теңдеулер жүйесінің (1. 1. 10) (1. 1. 11) анықтауышы Вронский анықтауышы
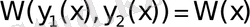
болғандықтан,
 нүктесінде нөл емес. Бұдан
нүктесінде нөл емес. Бұдан
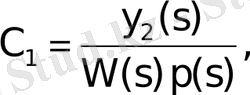
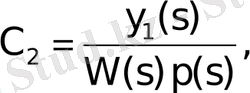
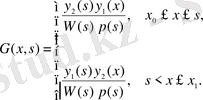 (1. 1. 12)
(1. 1. 12)
Мысал 2. Шеттік есептің Грин функциясын табу керек
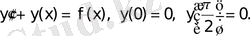
Шешуі. Тиісті біртекті теңдеудің
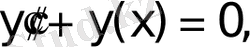
берілген шарттарды
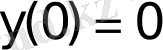 және
және
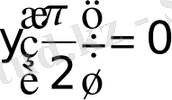
орындайтын шешімдері
 және
және

болғандықтан, (1. 1. 12) формула бойынша
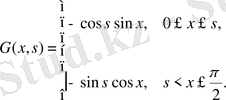
Ескерту .
(1. 1. 9) теңдеуінің у(х)
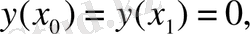 нолдік шекаралық шарттарын қанағаттандыратын біртекті теңдеуінің шешімі жоқ екендігін ұсынған болатынбыз. Бұл шарттардан (1. 1. 4) -(1. 1. 5) Грин функциясы жалғыздығына емес шеттік шарттарының бар болуы ғана емес жалғыздығына кепіл бола алады. Шындығында, егер Грин функциясының екі түрі бар болса
нолдік шекаралық шарттарын қанағаттандыратын біртекті теңдеуінің шешімі жоқ екендігін ұсынған болатынбыз. Бұл шарттардан (1. 1. 4) -(1. 1. 5) Грин функциясы жалғыздығына емес шеттік шарттарының бар болуы ғана емес жалғыздығына кепіл бола алады. Шындығында, егер Грин функциясының екі түрі бар болса
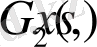 онда (1. 1. 4), (1. 1. 5) шеттік есептері үшін екі түрлі шешім аламыз.
онда (1. 1. 4), (1. 1. 5) шеттік есептері үшін екі түрлі шешім аламыз.
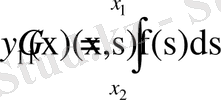
және
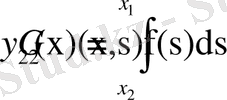
ерекшеліктері
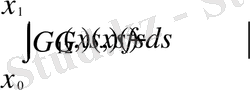
болжам негізінде, біртекті теңдеудің нетривиальды шешімдері, нөлдік шеттік шарттарды қанағаттандырады.
1. 2 ДЕРБЕС ТУЫНДЫЛЫ ЕКІНШІ РЕТТІ ТЕҢДЕУЛЕР КЛАССИФИКАЦИЯСЫ
Тәуелсіз х, у айнымалыларын, белгісіз u(x, y) функциясын және оның бірінші, екінші ретті дербес туындыларын байланыстыратын мынадай
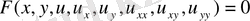 .
.
теңдеуді тәуелсіз екі айнымалыларына тәуелді екінші ретті дербес туындылы теңдеу деп атаймыз.
Ал мына
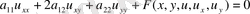 (1. 2. 1)
(1. 2. 1)
түрдегі теңдеуді жоғары ретті туындыларға қарағанда сызықтық теңдеу деп атайды, мұндағы
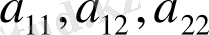 коэффиценттері х пен у айнымалыларының функциялары.
коэффиценттері х пен у айнымалыларының функциялары.
Егер (1. 2. 1) теңдеудегі
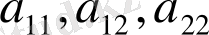 коэффиценттері u(x, y) функция мен оның бірінші ретті туындыларына тәуелді болса, яғни
коэффиценттері u(x, y) функция мен оның бірінші ретті туындыларына тәуелді болса, яғни
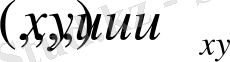 теңдеу онда
квазисызықтық
деп аталады.
теңдеу онда
квазисызықтық
деп аталады.
Егер теңдеу жоғары ретті
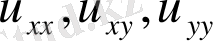 туындыларымен бірге u(x, y) фунциясына және оның бірінші ретті
туындыларымен бірге u(x, y) фунциясына және оның бірінші ретті
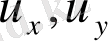 туындыларына қарағанда сызықтық теңдеу болса, ондай теңдеуді сызықтық теңдеу деп атаймыз және былай
туындыларына қарағанда сызықтық теңдеу болса, ондай теңдеуді сызықтық теңдеу деп атаймыз және былай
 (1. 2. 2)
(1. 2. 2)
жазамыз, мұнда
 тек x, y айнымалыларына тәуелді функциялар.
тек x, y айнымалыларына тәуелді функциялар.
Егер (1. 2. 2) теңдеудің барлық коэффициенттері х, у айнымалыларына тәуелсіз болса, онда (1. 2. 2) теңдеуді тұрақты коэффциентті сызықтық теңдеу деп атайды.
Ал егер (1. 2. 2) теңдеудегі f(x, y) 0 болса, онда теңдеуді біртекті теңдеу деп аталады.
Кері түрлендіруі бар
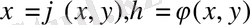
түрлендіруінің көмегімен (1. 2. 1) теңдеуді оған эквивалентті ең қарапайым формаға келтіруге болады .
Теңдеуді жаңа айнымалы арқылы
 (1. 2. 3)
(1. 2. 3)
Енді (1. 2. 3) формуланы
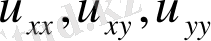 туындыларының мәндерін (1. 2. 1) теңдеуге қойып, мына түрге келеміз:
туындыларының мәндерін (1. 2. 1) теңдеуге қойып, мына түрге келеміз:
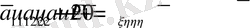 (1. 2. 4)
(1. 2. 4)
мұндағы
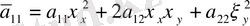
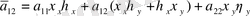
 функциясы екінші ретті туындыға тәуелсіз. Егер
функциясы екінші ретті туындыға тәуелсіз. Егер
 функциясы сызықты болса, онда
функциясы сызықты болса, онда
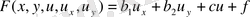 ,
,
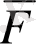 келесі түрде болады
келесі түрде болады
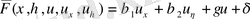
және (1. 2. 4) теңдеу сызықты болады.
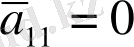 болатындай етіп
болатындай етіп
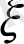 және
және
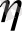 айнымалыларын таңдаймыз. Бірінші ретті теңдеуді дербес туынды ретінде қарастырамыз.
айнымалыларын таңдаймыз. Бірінші ретті теңдеуді дербес туынды ретінде қарастырамыз.
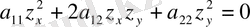 (1. 2. 5)
(1. 2. 5)
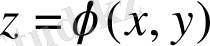 функциясы осы теңдеудің дербес шешімі болсын. Егер
функциясы осы теңдеудің дербес шешімі болсын. Егер
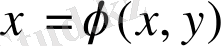 десек, онда коэффицентті нөлге тең болады. Осылайша, жоғарыдағы есептің айнымалыларды таңдау (1. 2. 5) есептің шешіміне байланысты болады.
десек, онда коэффицентті нөлге тең болады. Осылайша, жоғарыдағы есептің айнымалыларды таңдау (1. 2. 5) есептің шешіміне байланысты болады.
Келесі леммаларды дәлелдейміз.
Лемма 1. 2. 1 : Егер
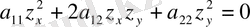
теңдеудің
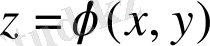 дербес шешімі болса, онда
дербес шешімі болса, онда
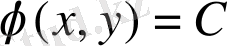 мына теңдеудің
мына теңдеудің
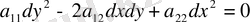 (1. 2. 6)
(1. 2. 6)
теңдеудің жалпы интегралы болады.
Лемма 1. 2. 2:
Егер
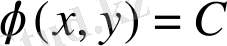 дифференциал теңдеудің
дифференциал теңдеудің
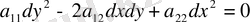 жалпы интегралы болса, онда
жалпы интегралы болса, онда
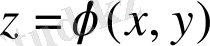 функциясы (1. 2. 5) теңдеуді қанағаттандырады.
функциясы (1. 2. 5) теңдеуді қанағаттандырады.
Лемма 1. 2. 1 дәлелдеу:
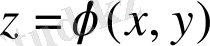 функциясы (1. 2. 5) теңдеуді қанағаттандыратын болғандықтан, онда теңдік
функциясы (1. 2. 5) теңдеуді қанағаттандыратын болғандықтан, онда теңдік
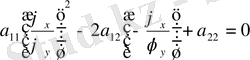 (1. 2. 7)
(1. 2. 7)
тепе-теңдігін аламыз. Шешімдер облысында х пен у-тің барлығын қанағаттандырады.
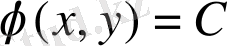 теңдеуіне байланысты (1. 2. 6) теңдеудің жалпы интегралы болады, егер у функциясы
теңдеуіне байланысты (1. 2. 6) теңдеудің жалпы интегралы болады, егер у функциясы
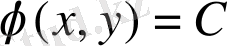 қатысты белгісіз және (1. 2. 6) теңдеуді қанағаттандыратын болса.
қатысты белгісіз және (1. 2. 6) теңдеуді қанағаттандыратын болса.
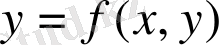 функциясы бар болсын, онда
функциясы бар болсын, онда
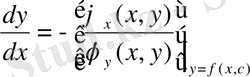 , (1. 2. 8)
, (1. 2. 8)
болады. Енді (1. 2. 6) теңдеуді шамасына бөліп, (1. 2. 8) формуланы пайдаланғанда мынадай
 (
(
 )
)
өрнекке келеміз. Квадрат жақшалардың ішіндегі өрнек тек
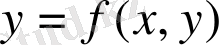 үшін ғана емес, кез келген х, у үшін нөлге тең. Сонымен 1. 2. 1-теорема дәлелденді.
үшін ғана емес, кез келген х, у үшін нөлге тең. Сонымен 1. 2. 1-теорема дәлелденді.
Лемма 1. 2. 2 дәлелдеу
: (1. 2. 6) теңдеудің
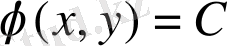 жалпы интегралы болсын. (х, у) кез-келген нүктесі үшін (х
0
, у
0
) берілген нүкте болсын. Егер біз (
жалпы интегралы болсын. (х, у) кез-келген нүктесі үшін (х
0
, у
0
) берілген нүкте болсын. Егер біз (
 ) теңдікті қанағаттандыратын дәлелдесек, онда кез-келген (х
0
, у
0
) (
) теңдікті қанағаттандыратын дәлелдесек, онда кез-келген (х
0
, у
0
) (
 ) теңдікке тепе-тең және
) теңдікке тепе-тең және
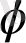 (х) функциясы (
(х) функциясы (
 ) теңдеудің шешімі болады. (1. 2. 6) теңдеуге (х
0
, у
0
) нүктесі арқылы интеграл қисығын жүргіземіз.
) теңдеудің шешімі болады. (1. 2. 6) теңдеуге (х
0
, у
0
) нүктесі арқылы интеграл қисығын жүргіземіз.
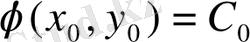 деп
деп
 қисығын жүргіземіз.
қисығын жүргіземіз.
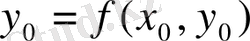 екені белгілі. Осы қисықтағы барлық нүктелер үшін:
екені белгілі. Осы қисықтағы барлық нүктелер үшін:
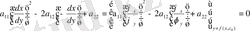
соңғы теңдіктегі
 десек, онда
десек, онда
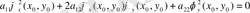
болды. Лемма дәлелденді.
(1. 2. 1) теңдеу үшін (1. 2. 6) теңдеу характеристикалық деп, ал интегралы характеристикасы деп аталады.
(1. 2. 6) теңдеудің жалпы интегралы бар
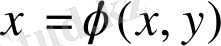 мұндағы
мұндағы
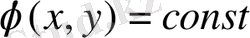 десек,
десек,
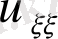 арқылы коэффиценттерін нөлге айналдырамыз. Егер (1. 2. 6) теңдеудің жалпы интегралы
арқылы коэффиценттерін нөлге айналдырамыз. Егер (1. 2. 6) теңдеудің жалпы интегралы
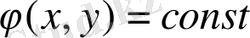 болса,
болса,
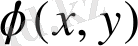 функциясына тәуелсіз болса, онда
функциясына тәуелсіз болса, онда
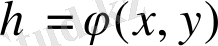 деп, біз
деп, біз
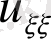 арқылы коэффиценттерін нөлге айналдырамыз.
арқылы коэффиценттерін нөлге айналдырамыз.
(1. 2. 6) теңдеуді екіге бөлеміз:
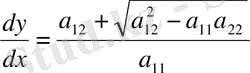 (1. 2. 9)
(1. 2. 9)
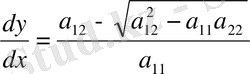 (1. 2. 10)
(1. 2. 10)
түбір астындағыларға өрнектің таңбасы (1. 2. 1) теңдеудің типін анықтаймыз.
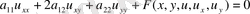 (1. 2. 1)
(1. 2. 1)
Егер М(х, у) нүктесінде
∆М(х, у) >0 болса, онда (1. 2. 1) теңдеу г и п е р б о л а л ы қ ,
∆М(х, у) <0 болса, онда (1. 2. 1) теңдеу э л л и п т и к а л ы қ ,
∆М(х, у) =0 болса, онда (1. 1. 2. 2. 1) теңдеуді п а р а б о л а л ы қ дейміз.
Қатынастың дұрыстығына көз жеткізу қиын емес
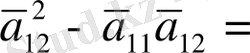 (
(
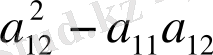 )
D
2
)
D
2
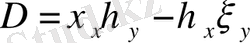
D Якоби анықтауышы нөлден өзгеше. Облыстың әртүрлі нүктеде әртүрлі типтегі теңдеуге жатуы мүмкін.
G облысын қарастырамыз, бұл облыстың барлық нүктелерінде бірдей типке жататын теңдеулер болсын. G облысының әрбір нүктесінен екі характеристикасы жүреді, гиперболалық типтегі теңдеу үшін нақты және әртүрлі, эллиптикалық типтегі теңдеу үшін комплексті және әртүрлі, ал параболалық типтегі теңдеу үшін екі характеристика нақты және бірдей болады.
Осы жағдайларды жеке-жеке қарастырамыз:
- >0 гиперболалық типтегі теңдеу үшін және (1. 2. 9) бен (1. 2. 10) оң жағын нақты және әртүрлі. Жалпы интегралыжәненақты характеристика үйірімен анықталады. деп (1. 2. 4) теңдеуге келеміз. арқылы коэффиценттерге бөлеміз. келесі түрге келеді:

Бұл гиперболалық типтің канондық түрі деп аталады. Көбінесе екінші канондық формуланы қолданады:
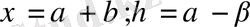
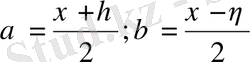
мұндағы
 және
және
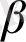 жаңа айнымалы. Онда
жаңа айнымалы. Онда
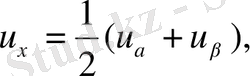
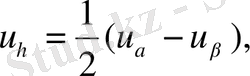
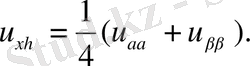
соңында (1. 2. 4) теңдеу келесі түрге келеді:
Ал теңдеу гиперболалық типті теңдеудің
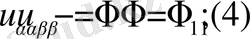
канондық формасының екінші түрі болады.
- =0 параболалық теңдеу үшін (1. 2. 9) бен (1. 2. 10) теңдеулер сәйкес
келеді. (1. 2. 6) жалпы интеграл үшін бір ғана интеграл интеграл аламыз:
 . Бұл жағдайда
. Бұл жағдайда
 және
және
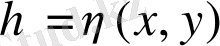 деп аламыз. Мұндағы
деп аламыз. Мұндағы
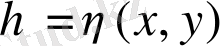 жаңа функция, функциясына тәуелсіз. Айнымалыларының коэффиценттерін тандаймыз.
жаңа функция, функциясына тәуелсіз. Айнымалыларының коэффиценттерін тандаймыз.
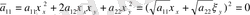
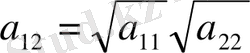 тең болғандықтан
тең болғандықтан

(1. 2. 4) теңдеуді
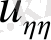 арқылы коэффиценттерін бөлгенде
арқылы коэффиценттерін бөлгенде

параболалық теңдеудің канондық теңдеуін аламыз. Егер оң жағынан шықпаса, онда бұл теңдеу параметріне тәуелді қарапайым дифференциал теңдеу болады.
1. 2. 3.
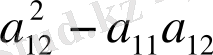 <0 эллиптикалық теңдеу үшін (1. 2. 9) бен (1. 2. 10) оң жағы комплекс болады.
<0 эллиптикалық теңдеу үшін (1. 2. 9) бен (1. 2. 10) оң жағы комплекс болады.
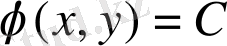 комплексті интегралы болсын. Онда
комплексті интегралы болсын. Онда
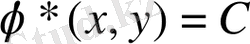
мұндағы
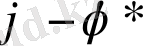 функциясының түйіндесі, (1. 2. 10) теңдеудің жалпы түйіндес интегралы болады.
функциясының түйіндесі, (1. 2. 10) теңдеудің жалпы түйіндес интегралы болады.
Енді комплексті айнымалыға көшеміз. Бұл жағдайда эллиптикалық типтегі теңдеу гиперболалық типке келеді.
Комплекс айнымалылармен жұмыс істемеу үшін жаңа айнымалы енгіземіз
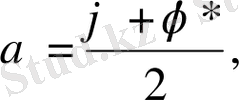
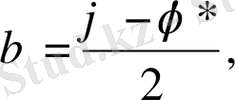 .
.
Осыдан
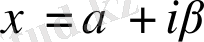 ,
,
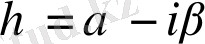 .
.
Бұл жағдайда
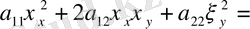 (
(
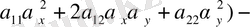
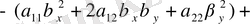
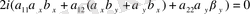
(1. 2. 4) теңдеуді
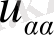 арқылы коэффиценттерге бөлгенде, мына түрге келеді.
арқылы коэффиценттерге бөлгенде, мына түрге келеді.
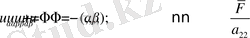 .
.
Осылайша
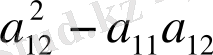 байланысты болған канондық теңдеу
байланысты болған канондық теңдеу
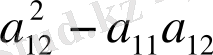 >0 (
гиперболалық типтегі
)
>0 (
гиперболалық типтегі
)
 немесе
немесе
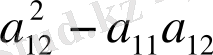 <0 (
эллиптикалық типтегі
)
<0 (
эллиптикалық типтегі
)
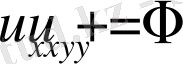
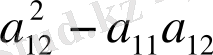 =0 (
параболалық типтегі
)
=0 (
параболалық типтегі
)
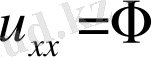
Көп айнымалыдан тәуелсіз екінші ретті теңдеудің классификациясы. Нақты коэффицентті сызықты теңдеуді қарастырайық,
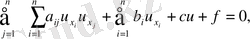
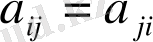 (1. 2. 12)
(1. 2. 12)
мұндағы
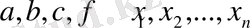 функциясы болады. Жаңа тәуелсіз
функциясы болады. Жаңа тәуелсіз
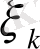 айнымалысын енгіземіз.
айнымалысын енгіземіз.
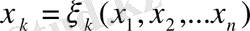 (k=1…n)
(k=1…n)
онда
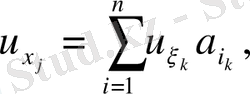
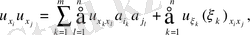
 мұндағы
мұндағы
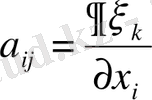 .
.
Жоғарыда алынған нәтижеден, төмендегі теңдеуге келеді:
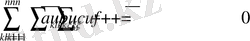
мұндағы
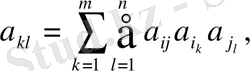
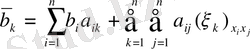
Квадраттық формасын қарастырамыз:
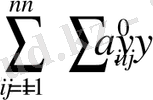
коэффиценттеріне тең коэффиценттер алдыңғы теңдеудің коэффициенттерінің кейбір нүктелеріндегі коэффиценттеріне тең
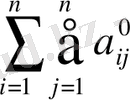 (1. 2. 13)
(1. 2. 13)
y= алмастыру арқылы жаңа квадраттық форма аламыз.
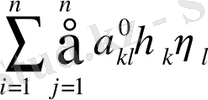 мұндағы
мұндағы
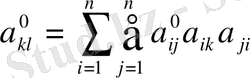
Сызықты түрлендіру арқылы матрица
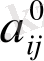 квадраттық формадан диагональды түрге келтіруге болады:
квадраттық формадан диагональды түрге келтіруге болады:
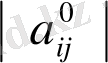 =1 немесе 0;
=1 немесе 0;
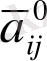 =0 (i
j, i, j=1, 2, …n) .
=0 (i
j, i, j=1, 2, …n) .
Инерция заңы бойынша, сызықты түрлендіруге байланысты канондық түрдегі квадраттық форманың оң, теріс және коэффиценті нөлге тең болатын инвариант арқылы анықталады. (1. 2. 12) теңдеуінің М
0
нүктедегі эллиптикалық теңдеу дейміз, егер барлық n қосындылар таңбасы бірдей болса; гипреболалық теңдеу дейміз егер n-1 барлық
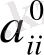 коэффиценттері бірдей болса, және қандайда бір коэффиценті қарама-қарсы таңбалы болса; ультрагиперболалық типті дейміз, егер
коэффиценттері бірдей болса, және қандайда бір коэффиценті қарама-қарсы таңбалы болса; ультрагиперболалық типті дейміз, егер
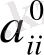 коэффиценттері арасында m коэффицентті бірдей таңбалы, ал n-m коэффиценттері қарама-қарсы таңбалы болса (m, n-m>1) ; парболалық дейміз, егер
коэффиценттері арасында m коэффицентті бірдей таңбалы, ал n-m коэффиценттері қарама-қарсы таңбалы болса (m, n-m>1) ; парболалық дейміз, егер
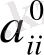 коэффиценттерінің кем дегенде біреуі нөлге тең болса.
коэффиценттерінің кем дегенде біреуі нөлге тең болса.
Жаңа тәуелсіз айнымалы
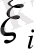 аламыз.
аламыз.
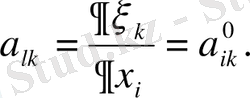
мұндағы
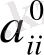 -(1. 2. 13) квадраттық форманы канондық түрге келтіретін түрлендіру коэффицентті; (мысалы,
-(1. 2. 13) квадраттық форманы канондық түрге келтіретін түрлендіру коэффицентті; (мысалы,
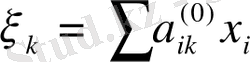 десек) онда М
0
нүктеде теңдеудің типіне тәуіелді келесі түрдегі канондық форманың біріне келеді:
десек) онда М
0
нүктеде теңдеудің типіне тәуіелді келесі түрдегі канондық форманың біріне келеді:
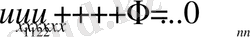 (эллиптикалық тип)
(эллиптикалық тип)
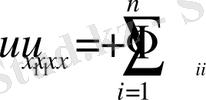 (гиперболалық тип)
(гиперболалық тип)
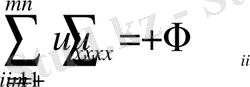 (m>1, n-m>1) (ультрагиперболалық тип)
(m>1, n-m>1) (ультрагиперболалық тип)
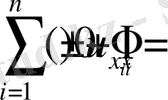 (m>0) (параболалық тип)
(m>0) (параболалық тип)
осылайша, (1. 2. 12) теңдеу кейбір М нүктелі белгіл бір типке тиісті болса, онда сәйкесінше осы нүктеде канондық түрге келтіруге болады.
Енді М нүкте маңайында теңдеуді канондық формаға келтіруге бола ма, егер сол нүкте маңайында теңдеу тек бір типке жататын болса деген сұрақты қарастырамыз.
Кейбір облыста теңдеуді канондық түрге келтіру үшін
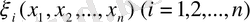 функциясы
функциясы
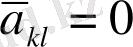 қатысты
қатысты
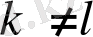 дифференциалдау керек болатын. Мына шартта n(n-1) /2 функциясын n анықтау керек n=3 үшін матрицасын диагоналынан басқа элементтерін нөлге айналдыруға да болар еді, бірақ диагональ элементтері әртүрлі болып қалады. n≥3 те М нүкте маңайында теңдеуді канондық түрге келтіруге болмайды. n=2 үшін диагональдық коэффиценттерінен басқа бір элементті нөлге айналдырады және екі диагональдық коэффицент шартын қанағаттандырады.
дифференциалдау керек болатын. Мына шартта n(n-1) /2 функциясын n анықтау керек n=3 үшін матрицасын диагоналынан басқа элементтерін нөлге айналдыруға да болар еді, бірақ диагональ элементтері әртүрлі болып қалады. n≥3 те М нүкте маңайында теңдеуді канондық түрге келтіруге болмайды. n=2 үшін диагональдық коэффиценттерінен басқа бір элементті нөлге айналдырады және екі диагональдық коэффицент шартын қанағаттандырады.
Егер (1. 2. 12) теңдеудің коэффиценттері тұрақты болса, онда М нүктеде (1. 2. 12) теңдеу канондық түрге келеді.
Тұрақты коэффицентті сызықты теңдеудің канондық формасы .
Екі айнымалыдан тәуелді екінші ретті тұрақты коэффицентті теңдеу мына
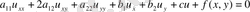 (1. 2. 14)
(1. 2. 14)
түрде болады.
Оған тұрақты коэффицентті (1. 2. 6) характеристикалық теңдеу сәйкес келеді. Сондықтан характеристикалық теңдеу шешімдері
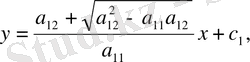

(1. 2. 14) теңдеуді сәйкінше түрлендіріледі.
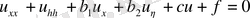 (эллиптикалық тип) (1. 2. 15)
(эллиптикалық тип) (1. 2. 15)
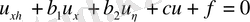 (гиперболалық тип) (1. 2. 16)
(гиперболалық тип) (1. 2. 16)
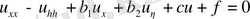
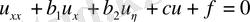 (параболалық тип) (1. 2. 17)
(параболалық тип) (1. 2. 17)
Қарапайым түрге келтіру үшін u функциясын жаңа v функциясымен алмастырамыз.
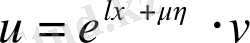
мұндағы
 -алі анықталмаған тұрақты. Онда
-алі анықталмаған тұрақты. Онда
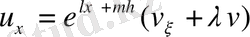
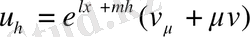
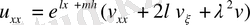
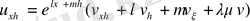
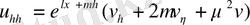
(1. 2. 15) теңдеуге қойып және
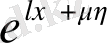 қысқарту арқылы
қысқарту арқылы
 .
.
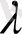 және
және
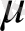 параметрлерін екі коэффиценті, мысалы бірінші ретті туындысы нөлге айналатындай (𝜆=
) етіп таңдаймыз. Нәтижесінде
параметрлерін екі коэффиценті, мысалы бірінші ретті туындысы нөлге айналатындай (𝜆=
) етіп таңдаймыз. Нәтижесінде

теңдеуін аламыз. Мұндағы арқылы анықталады. (1. 2. 16) және (1. 2. 17) теңдеулері үшін аналогиялық операциялар жүргізе отырып, тұрақты коэффициенті теңдеудің канондық түріне келеміз:
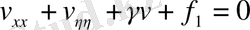 (эллиптикалық тип)
(эллиптикалық тип)
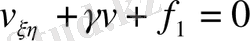
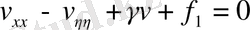 (гиперболалық тип)
(гиперболалық тип)
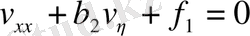 (параболалық тип)
(параболалық тип)
2-пункте айтылғандай тұрақты коэффицентті теңдеулер бірнеше тәуелсіз айнымалылар жағдайында
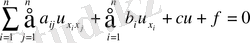 .
.
Сызықтық түрлендіру айнымалыларының көмегімен барлық нүктелер облысының бір мезетте канондық түрін анықтайды. арқылы облыстың барлық нүктеде бірдей канондық түрге келеді.
 функциясының орнына жаңа
функцияларын енгізе отырып
функциясының орнына жаңа
функцияларын енгізе отырып
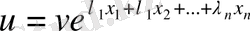
теңдеуін аламыз.
1. 3 ПАРАБОЛАЛЫҚ ТЕКТЕС ТЕҢДЕУГЕ ҚОЙЛАТЫН ҚОСЫМША ШАРТТАР
Ұзындығы
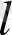 біртекті стержень қарастырылады, бүйір беттері жылу өткізбейтін, жіңішке, көлденең қимасындағы температура кез келген уақытта тұрақты. Егер стержень ұштарында температура тұрақты
біртекті стержень қарастырылады, бүйір беттері жылу өткізбейтін, жіңішке, көлденең қимасындағы температура кез келген уақытта тұрақты. Егер стержень ұштарында температура тұрақты
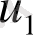 және
және
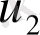 болса, онда стержень бойында жылу таралуы сызықты болады. (36-сурет)
болса, онда стержень бойында жылу таралуы сызықты болады. (36-сурет)
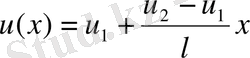 (1. 3. 1)
(1. 3. 1)

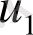
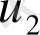
x
Сондықтан, температуралы нүктеден жылу таралады, стержень бойымен жоғары температуралы нүктеден төменгі соңында қатты ыстықтан жай ыстыққа жылу таралады.
Бірлік уақыт ішінде стерженнің нүктедегі ауданы S, жылу мөлшері эксперимент формуласын береді:
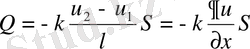 (1. 3. 2)
(1. 3. 2)
мұндағы, k-стержень материалына байланысты жылу өткізгіш коэффицентті.
Жылу таралу мөлшері оң анықталған дейміз, егер х нүктесіне қарай өсетін болса. Стержень бойында жылу таралу процесін қарастырамыз. Бұл процесс u(x, y) функциясы арқылы бейнеленеді. t уақыт моментінде х нүктесіндегі температураны береді.
u(x, y) функциясын қанағаттандыратын теңдеу іздестіреміз. Бұл үшін физиканың жылу таралу заңдылықтарын қолданамыз.
Фурье заңы. Егер дененің температурасы тепе-тең болмаса, онда оның ішінде жылу ағымдары пайда болады. Температура жоғарыдан төменге бағытталады. Жылу мөлшерінің таралуы х нүктесі (t, t+dt) аралығында
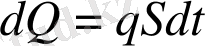 (1. 3. 3)
(1. 3. 3)
тең. Мұндағы
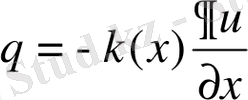 (1. 3. 4)
(1. 3. 4)
Жылу ағынының тығыздығы, бір уақыт мөлшерінде 1см 2 ауданынан өтетін жылу мөлшеріне тең. Бұл заңдылық (1. 3. 2) формуланың жалпы түрі . Оған да интегралдық формула беруге болады:
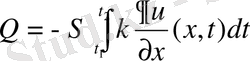 (1. 3. 5)
(1. 3. 5)
мұндағы Q-x нүктесіндегі [t 1 , t 2 ] аралығында таралған жылу мөлшері. Егер стержень біртекті емес болса, онда k x-тің функциясы болады.
2.
 температурасын көтеру үщін біртекті дененің жылу мөлшерін анықтау керек . ол үшін
температурасын көтеру үщін біртекті дененің жылу мөлшерін анықтау керек . ол үшін
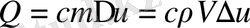
мұндағы m-дененің массасы,
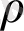 тығыздығы, V-көлемі.
тығыздығы, V-көлемі.
Егер температураны өзгертсек, онда стержень температурасы әр жерінде әртүрлі мөлшерлі немесе біртекті емес болса, онда
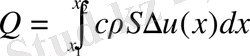 . (1. 3. 7)
. (1. 3. 7)
3. Стержень ішінде жылу пайда болса немесе сіңіретін болса, t моментінде х нүктесінің F(x, t) жылу тығыздығын сипаттауы мүмкін. (t, t+dt) уақыт аралығында (x, x+dx) стерженнің де жылу мөлшері келесі түрде болады:
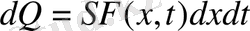 (1. 3. 8)
(1. 3. 8)
немесе интегралдық формада
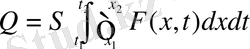 (1. 3. 9)
(1. 3. 9)
мұндағы, Q-(t 1 , t 2 ) уақыт аралығында (х 1 , х 2 ) стержень бойындағы жылу мөлшері.
(t 1 , t 2 ) уақыт аралығындағы (х 1 , х 2 ) кесіндісінде жылу баланс есебінен жылу өткізкіштің теңдеуі шығады. Энергия сақталу заңдылықтар және (1. 3. 5), (1. 3. 7), (1. 3. 9) формулаларын пайдалана отырып келесі теңдікті аламыз:
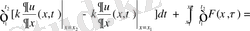
=
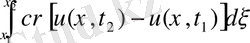 (1. 3. 10)
(1. 3. 10)
(1. 3. 10) жылу өткізгіштің интегралдық формасы.
Интегралдық формадан дифференциалдық формаға көшеміз. Ол үшін орташа мән теоремасы мен ақырлы өсімшелер теоремасын қолдананамыз.
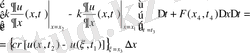 (1. 3. 11)
(1. 3. 11)
Соңғы түрлендіру арқылы келесі түрге келеміз:
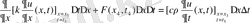 (1. 3. 12)
(1. 3. 12)
мұндағы t 3 , t 4 , t 5 және x 3 , x 4 , x 5 -(t 1 , t 2 ) және (x 1 , x 2 ) интервалындағы нүктелер.
(1. 3. 12) формуланы
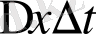 -ға бөлеміз.
-ға бөлеміз.
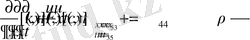 (1. 3. 13)
(1. 3. 13)
Бұл түрлендірулер (t
1
, t
2
) және (x
1
, x
2
) интервал аралығындағы туындыға байланысты қарастырылады.
 шекке көшеміз.
шекке көшеміз.
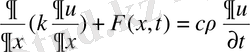 (1. 3. 14)
(1. 3. 14)
(1. 3. 14) - жылу өткізгіштің теңдеуі .
Дербес жағдайларды қарастырайық.
1. Егер стержень біртекті болса, онда k, c, p -тұрақты деп келесі теңдеуге келеміз.
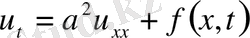
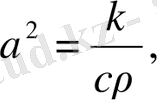
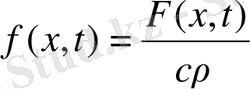
мұндағы -
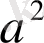 тұрақты, температура өткізгіш коэффицентті. Егер
тұрақты, температура өткізгіш коэффицентті. Егер
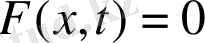 болса, онда жылу өткізгіш теңдеуі
болса, онда жылу өткізгіш теңдеуі
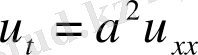 (1. 3. 14’)
(1. 3. 14’)
болады.
Жылу көлемінің тығыздығы температураға байланысты болуы мүмкін. Ньютон заңындағы қоршаған орта мен жылу алмасуы стержень бойында
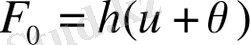
тең болады, мұндағы -
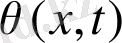 қоршаған орта температурасы, h-жылу мөлшерін коэффицентті t моментте х нүктесінде мынаған
қоршаған орта температурасы, h-жылу мөлшерін коэффицентті t моментте х нүктесінде мынаған
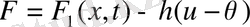 (1. 3. 15)
(1. 3. 15)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz