Биомембрана арқылы зат тасымалдау

Пән: Медицина
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Биомембрана арқылы зат тасымалдау

Лекция жоспары

Биологиялық мембранның өткізгіштігі туралы түсінік. Жасуша өткізгіштігі.
Пассивті тасымалдау және оның түрлері: диффузия, жеңілдетілген диффузия, осмос және фильтрация.
Ионоформдар.
Активті тасымалдау және оның механизмі.
Ион каналдары арқылы зат тасымалдау ерекшелігі.
Потенциалға «тәуелді» және «тәуелсіз» иондық каналдар.

Лекция мақсаты: биологиялық мембрананың заттарды өткізуін және оның түрлерін, пассивті және активті тасымалдауды, биомембранадағы иондық каналдардың заттарды өткізу ерекшеліктерін талдау.

Жасуша ашық термодинамикалық жүйе болғандықтан өзін қоршаған ортамен үнемі зат, энергия және ақпарат алмасады. Мұндай алмасу жасуша мембранасының түрлі заттарды өткізу қабілеті арқасында іске асады. Жасушаның мұндай қабілетін - өткізгіштік деп атайды. Жасушадағы метоболизм, биопотенциалдың пайда болуы, нерв импульстарнының таралуы және т. б. көптеген құбылыстар мембранадағы зат тасымалдау арқасында жүреді және пайда болады. Сондықтан, биологиялық мембрана арқылы зат тасымалдау- жасаушаның өмір сүруінің негізгі шарты. Зат тасымалдаудың бұзылуы түрлі патологиялық құбылыстарға алып келеді. Сондықтан тасымалдау құбылысын зерттеудің медицина және фармация үшін үлкен теориялық және практикалық маңызы бар.

Адам ағзасын емдеу шаралары дәрілік заттардың жасуша мембранасы арқылы өту деңгейіне байланысты, ал ол өз кезегінде мембрананың өткізгіштігіне тәуелді. Бұл жағдай жаңа дәрілік қосылыстарды дайындаушы фармацевтердің жасушаның қалыпты және патология кезіндегі дәрілік заттардың мембрана арқылы тасымалдау ерекшеліктерін ескеруін қажет етеді.

БМ арқылы зат тасымалдауды транспорт деп те атайды, ол екі түрге бөлінеді: пассивті тасымалдау (транспорт) және активті тасымалдау (транспорт) .

Пассивті тасымалдау (ПТ) деп, зарядсыз бөлшектерді (заттарды) концентрациясы көп С ₁ ортадан концентрациясы аз ортаға қарай тасымалдауды, зарядталған бөлшектерді (заттарды) электр өрісінің потенциалы жоғары ϕ ₁ ортадан, потенциал шамасы төмен ϕ ₂ ортаға қарай тасымалдауды, немесе электрохимиялық потенциалы жоғары μ ₁ нүктеден, электрохимиялық потенциалы төмен μ ₁ нүктеге қарай тасымалдауды атайды. Аталған тасымалдаудың бұл түрлерінде сырттан энергия жұмсалмайды, жүйе ішінде концентрациялық, электрлік, электрохимиялық, гравитациялық т. б. градиентте жинақталған энергия қоры есебінен жүреді. Осы жерде градиент деген физикалық түсінікті қарастыра кетейік. Мысал ретінде концентрациялық градиенті қарастырайық, ол мына түрдегі өрнекпен анықталынады: gradC = С ₁ - С ₂ /х = ∆C/х , мұндағы С ₁ және С ₂ ара қашықтығы х болатын екі нүктедегі ерітіндінің концентрациясы, осы тәрізді электр өрісінің градиенті gradЕ = Е ₁ - Е ₂ / l = ∆E/х түрінде сипатталады. Сонымен градиент деп, физикалық шаманың белгілі бір бағыттағы бірлік қашықтықа сәйкес келетін өзгерісін сипатайтын шаманы атаймыз. Мысалы, ара қашықтығы 10 см болатын екі нүктенің бірінші нүктесіндегі ерітінді концентрациясы 45%, ал екі нүктесінде 20% болса, онда жоғарыдағы өрнекке сәйкес концентрациялық градинет gradC = С ₁ - С ₂ /х = 45% - 20%/10см = 2, 5%/см тең болар еді, яғни бұл деген бірінші нүктеден екінші нүктеге қарай бір сантиметр сайын ерітінді концентрациясы 2, 5% өзгереді дегенді білдіреді.

Егер ортада бір мезгілде концентрациялық және электрлік градинет қатар келсе, онда қорытынды градиентті электрохимиялық градиент деп атайды.

Пассивті тасымалдау мынадай түрлерге бөлінеді ( 1- сурет) :

1 сурет

Енді қарапайым диффузия құбылысының механизмін талдайық. Дифффузия деп, зат молекулаларының хаостық жылулық қозғалысы нәтижесінде, өз беттерінше концентрациясы көп ортадан аз ортаға қарай тасымалдануын айтамыз және ол концентрациялық градиент есебінен жүреді және Фик заңына бағыады.

Тасымалданатын заттың мөлшерін зат ағыны деген шамамен сипаттайды. Зат ағын Ф деп, диффузия бағытына перпендикуляр орналасқан, көлденең қимасы S болатын жерден, бірлік уақыт ішінде тасымалданған зат мөлшерін атайды және ол мына өрнекпен сипатталады:

Ф= - D⋅S⋅dc/dx,

мұндағы Ф- зат ағынының мөлшері, D- диффузия коэффициенті, dc/dx- концентрациялық градиент. Өрнектегі «-» минус таңбасы зат ағыны концентрацияның кемуі бағыты бойынша жүретіндігін білдіреді. Көбіне бұл өрнекті зат ағынының тығыздығы J арқылы сипаттайды және оны диффузия үшін Фик теңдеуі деп атайды:

J = Ф/S = - D⋅ dc/dx

мұндағы J- зат ағынының тығыздығы, D- диффузия коэффициенті, dc/dx- концентрациялық градиент. Өрнектегі «-» минус таңбасы зат ағыны концентрациялық градиентке қарсы бағыта жүретіндігін білдіреді.

Бұл өрнек арқылы зертханалық (лабораториялық) жағдайда диффузия құбылысын зерттеу, ондағы тасымалданатын зат мөлшерін анықтау және т. б. мәліметтерді анықтау қиындау. Осы себепті Фик теңдеуін қолдануға жеңіл және қарапайым түрге келтіруге болатын жолын қарастырайық. .

Тасмалдатын заттың полярлы және полярсыз еріткіштерде әр түрлі деңгейде еруі себепті мембрананың ішіндегі және сыртындағы орталардағы концентрациясы әр түрлі мәнге ие болады. Мембрананың сыртындағы ортадағы зат концентрациясы с ₁ , ішінде с ₂ , ал мембрананың сыртқы ортаға қараған ішкі бетіндегі зат концентрациясы с _м1 , ал оның ішкі ортаға қараған ішкі бетіндегі зат концентрациясы с _м2 болсын делік ( 2сурет) .

сыртқы орта ішкі орта

с ₁ с _м1

с _м2 с ₂

2 сурет

Мембрананың қалыңдығының өте аз болуы себепті ондағы концентрациялық градиентті тұрақты шама деп алуға болады. Егер с _м1 > c _м2 болса, онда концентрациялық градиент мынаған тең болады:

dc/dx = с _м2 - с _м1 / l

мұндағы, l -мембрана қалыңдығы. Бұл өрнекті Фик теңдеуіне қойсақ, онда мына түрдегі өрнек келіп шығады:

J = - D⋅ с _м2 - с _м1 / l

Тасымалданатын зат мөлшерінің мембрананың іші мен сыртқы орталарда таралу деңгейінің әр түрлі болуын сипттау үшін заттың таралу коэффициенті К деген түсінік ендіреміз, оны мына түрде жазайық:

К= с _м1 /с ₁ = с _м2 /с ₂ ,

мұндағы с ₁ және с ₂ сыртқы және ішкі орталардағы зат концентрациясы, с _м2 - мембранының ішкі ортаға қараған бетіндегі бөлшектер концентрациясы, с _м1 -мембрананың сыртқы ортаға қараған бетіндегі бөлшектер концентрациясы

Соңғы өрнектен с _м1 = Кс ₁ және с _м2 = Кс ₂ болатындығын анықтап, оны Фик теңдеуіне қойсақ:

J = - D⋅К⋅(c ₂ - с ₁ ) / l

мұндағы P= DK/ l шаманы өткізгіштік коэффициенті деп атайық, сонда Фик теңдеуі мына түрге келеді:

J = -P(c ₂ - c ₁ ),

мұндағы Р- мембрананың заттарды өткізгіштігін сипаттайтын шама.

Анықталған бұл өрнек диффузия құбылысын лабораториялық жағдайда зерттеуді жеңілдетеді.

Фик теңдеуі арқылы зарядталмаған және электр өрісі жоқ кезіндегі зарядталған бөлшектерді пассивті тасымалдау құбылысын сипаттайды, енді мембранадағы электр өріс кезіндегі тасымалдау құбылысын сипаттайтын өрнекті қорытып шығарайық.

Электр өрісінде тұрған ионға әсер ететін Кулон күші: f ₀ =qE тең, мұндағы Е- электр өрісінің кернеулігі, ал ионнның заряды мына өрнекпен сипатталады q= Ze, мұндағы Z - ионның валенттілігі. Электр өрісін электр потенциалының градиенті арқылы жазайық: Е = - dϕ/dx. Сонда ионға әсер ететін Кулон күші мына түрге келеді: f ₀ = -Ze⋅dϕ/dx. Соңғы өрнектің екі жағын да N _A Авогадро санына көбейтсек f = -ZF dϕ/dx өрнегі келіп шығады, мұндағы f = f ₀ N _A бір моль ионға әсер етуші күш, F =eN _A Фарадей тұрақтысы.

Тасымалданатын затқа (ионға) электр күшімен қатар ортаның кедергі күші де әсер етеді. Бұл күштер бір- бірін теңестіргендіктен зат бірқалыпты v жылдамдықпен тасымалданды, оның шамасы ионға әсер етуші күшке тура пропорционал v= b⋅f тең, мұндағы b - ионнның қозғалғыштық коэффициенті. Осы анықталған шамаға f күштің өрнегін қойсақ, жылдамдық мына түрге келеді:

v = -bZF⋅dϕ/dx

Мембрана арқылы тасымалданатын зат ағыны мына өрнекпен сипатталады: Ф =c⋅S⋅ v, мұндағы с- тасымалданатын зат концентрациясы, S-зат тасымалдатын аймақтың көлдеңен қимасының ауданы, v -тасымалдау жылдамдығы Осы өрнекке жоғарыда анықталған жылдамдықтың өрнегін қойсақ, онда электр өрісінде тасымалданатын зат ағынының өрнегін аламыз:

Ф =- cSb ZF dϕ/dx

Тасымалдататын зат ағынының тығыздығы мына түрде анықталынатындығын ескерсек: J = Ф/S, соңғы өрнек мына түрге келеді:

J = - cbZF dϕ/dx

Жалпы жағдайда бір мезгілде зат тасымалдау концентрациялық және электр өрісі градиенттері нәтижесінде жүрсе, онда соңғы өрнек мына түрде жазылады:

J = -D dc/dx - cbZF dϕ/dx

Бұл Нернст- Планк теңдеуі деп аталынады және ол ионның концентрациялық және потенциал градиенті әсерінен жүретін диффузиялық ағынның тығыздығын сипаттайды. Нейтрал бөлшектер үшін Z=0 болатындығын ескерсек, соңғы өрнек Фик теңдеуіне айналады. Сонымен біз пассивті тасымалдаудың заңдылықтарын анықтадық. Енді пассивті тасымалдаудың түрлерін қарастырайық ( 3- сурет) .

Қарапайым диффузиялипидтік қабат арқылы жүреді және Нернст-Планк теңдеуіне бағынады. Мұндай тасымалдаулар арқылы жасушаға оттегі, көміртегі газы, дәрілік заттар жеткізіледі. Бірақ қарапайым тасымалдау өте баяу жүретіндіктен жасушаны қажетті қоректік заттармен толық қамтамасыз ете алмайды.

C ₁

O ₂ Na ⁺ K ⁺ Na ⁺

Na ⁺

К ⁺

C ₂

A Б В Г

3 сурет. А- қарапайым диффузия, Б- иондық канал арқылы тасымалдау, В- жеңілдетілген диффузия, Г- эстафеталық тасымалдау.

Жеңілдетілген диффузия. Тасымалдаудың бұл түрі мембранадағы арнаулы ақуыздар- тасымалдағыштар арқылы іске асады. Олар мембрана арқылы табиғаты гидрофильді болатын, өз беттерінше мембрана арқылы өтуі өте төмен заттарды тасымалдайды. Мұдай тасымалдағыштар мембрана қабаты арқылы кейбір аминқышқылдарын, көмірсуларды, пуриндік және пиримидтік негіздерді, нуклезоидтарды тасымалдайды. Тамақтық заттардың ішекте сорылуы, бүйректегі реабсорбция және т. б. процесстер осы тасымалдаушылар арқылы жүреді.

Егер мембранада бір мезгілде жай және жеңілдетілген диффузия қатар жүрсе, онда мембрана арқылы заттарды тасымалдау жай диффузия ағыны мен жеңілдетілген диффузия ағынының қосындысына тең болады (4- сурет) . Жалпы жеңілдетілген диффузия жылдамдығы 10 ^-4 ион/с тең.

Графиктен, мебрана арқылы жеңілдетілген диффузия көмегімен зат тасымалдау қарқыны өте жоғары болатындығы көрініп тұр.

Кей оқулықтарда ион тасымалдағыштарды ионоформ деп атайды. Ионоформның сырты полярсыз молеулалар тобымен қапталған, сондықтан ол мембрананың гидрофобты аймағында жатады, ішкі қабатында иондарды қосып алуға арналған полярлы молекуламен қапталған бос қуыс бар. Ионоформдардың басым көпшілігі микроағзалардан алынған, бірақ синтетикалық жолмен алынғандар да кездеседі.

Мембрана арқылы зат тасымалдау құбылысын зерттеген Борнның теңдеуіне сәйкес, мембрана қабаты арқылы иондарды тасымалдауға қажетті энергия шамасы ионның радиусына кері пропорционал.

$\$ $\$ = $\frac{{}^{}{}_{}}{{}_{M}}\frac{{}^{}{}_{}}{{}_{}{}_{}}\left( \frac{}{}\frac{}{} \right),$ $\frac{{}^{}{}_{}}{{}_{M}}\frac{{}^{}{}_{}}{{}_{}{}_{}}\left( \frac{}{}\frac{}{} \right),$

мұндағы, ∆W- ион тасмалдағыш жұбының энергиясы, r- ион радиусы, b- тасымалдағыштың радиусы, ε _M - мембрананың диэлектрлік өтімділігі, ε _n - тасымалдағыштың ішкі сферасының диэлектрлік өтімділігі.

Тасымалдағыш ионды қосып алғанда пайда болған жұптың радиусы артады, жоғарыдағы теңдеуге сәйкес тасымалдау энергиясы азаяды. Жүргізілген есептеулер тасымалдағыш арқылы калии немесе натрии иондарын тасымалдауға 15 кДж/моль энергия жұмсалатындығын көрсетті, ал жай диффузия кезінде, тасымалдағаштың көмегінсіз аталған иондарды тасуға 250-300 кДж/моль энергия жұмсалады екен.

Тасымалдағыштардың көпшілігі нейтралды(зарядсыз) күйде болады, олар ортадан ионды қосып алып, зарядталған жұпқа айналады, ал кейбірі керісінше зарядталған болып келеді, мысалы нигерицин, ол өзіне ионды қосып алып нейтрал күйге көшеді.

Ақуыз тасымалданатын заттарды өзіне қосып алып диффузияланады. Бұл құбылыс валиномицин арқылы калии ионын тасымалдауда толық анықталған. Жүргізілген ғылыми зерттеулер мына жағдайды көрсетті, валиномицин өзіне калии ионын қосып алып, липид қабатында еритін қомплекс құрап, мембрананың екінші жағына өтеді де, калии ионын босатады, өзі қайта орнына келеді.

Эстафеталық тасымалдау. Мембрана қабатында орналасқан тасмалдаушы ақуыздар тасымалданатын затты бір біріне жеткізу арқылы іске асырады.

4. Осмос . Жасуша мембранасының жартылай өткізгіштік, яғни кей заттарды өткізетін, мысалы су молекуласын, ал кей заттарды өткізбейтін қасиеті бар. Осмос деп су молекуласының концентрациясы көп ортадан (бұл ортада еріген зат концентрациясы аз) аз ортаға (еріген зат концентрациясы көп) қарай мембрананың жартылай өткізгіштік қасиеті нәтижесінде тасымалдануын атайды. Мына мысалды талдайық: ыдыстың бір бөлігінде концентрациясы 40%, екінші бөлігінде 60% болатын тұз ертіндісі бір бірінен өткізгіштігі тұз үшін 0 тең, ал суды өткізетін қалқан арқылы бөлінген болсын делік, егер қалқанды алып тастасақ, онда 1 бөліктен су молекулалары 2 бөліке қарай тасымалданады НЕГЕ ? Өйткені 1-ші ортада (40 пайыз тұз, 60 пайыз су) су молекуласының концентрациясы 2-ші ортаға ( 60 пайыз тұз, 40 пайыз су) қарағанда көп, сондықтан су молекуласының тасымалдануы 1- ортадан ден 2- ге қарай жүреді.

Су молеулаларының әсерінен пайда болатын қысым осмостық деп аталады. Осмостық қысымдары бірдей ертінділерді изотондық деп атау келісілген. Ағза сұйықтығының осмостық қысымы физиологиялық ертінді қысымына тең, сондықтан оны ағза сұйығына салыстырғанда изотондық ертінді болып табылады. Егер ертіндің осмостық қысымы басқа ертіндінің осмостық қысымынан жоғары болса ондай ертіндіні гипертондық, керісінше болса, оны гипотондық ертінді деп атайды. Адам қанының осмостық қысымы 0, 76-0, 78 МПа аралығында жатыр, ал 0, 86% NaCl физиологиялық ертіндінің осмостық қысымы да дәл осындай.

Егер эритроцит жасушасын дистилляциоланған суға салсақ, онда су молекулалары оның ішіне еніп, жасуша ісінеді, оның порлары кеңіп, оның ішіндегі барлық заттар сыртқа шығып, жасауша мембранасы толығымен суға толады. Осылайша алынған мембрана қабықшаларын зерттеуге ыңғайлы. Егер жоғарыда аталған эксперименте эритроцитің ішіндегі заттар сыртқа шықпаса, онда ол ісініп, жасауша жарылып кетер еді, мұндай құбылысты «осмостық шок» деп атайды. Мұндай жағдай ағза көп мөлшерде тұзды ерітінді қабылдаған кезде байқалалы.

Керісінше жасаушадағы су молекулалары толығымен сыртқа шықса, яғни ағзаның сусыздануы байқалса, онда жасуша жиырлып, оның жансыздануы орын алады, яғни жасуша өмір сүруін тоқтатады. Мұндай құбылыс «коллапс» деп аталынады. Қан тамарлар жүйесіндегі қанның осмостық қысымын тұрақты деңгейде реттеп отыратын арнаулы альбумин деген ақуыз бар. Ағзадағы коллапс құбылысы көп қан кетудің әсерінен емес, қанның осмостық қысымының бірден төмендеуінен байқалады екен, сондықтан көп қан жоғалту кезінде ағзаға инерті жоғарымолекулалы қан ауыстырғыштарды салады, нәтижесінде қанның осмостық қысымы өз деңгейіне келеді.

5. Фильтация (сүзу, сүзгі) деп гидростатикалық қысым градиенті есебінен су молекулаларының мембрана порлары арқылы тасымалдануын атайды. Су молекулаларының тасымалдану жылдамдығы Пуайзель заңы бойынша жүреді: dV/dt = P ₁ - P ₂ /w, мұндағы dV/dt- суды тасымалдау жылдамдығы, w- гидравликлық қысым, ол w = 8 l η/πr ⁴ тең, l - пор ұзындығы, r- оның радиусы, η- судың тұтқырлдық коэффициенті. Фильтрация құбылысы қан тамырлары арқылы су молекуласын тасымадануда маңызды орын алады, кейбір патологияларда фильтрация күшейіп нәтижесінде дене ісінеді.

Активті тасымалдау(АТ ) . Мембрана арқылы зат тасымалдудың бұл түрі жүйенің химииялық энергиясы есебінен жүреді. Егер мембранада тасмалдау тек пассивті түрде жүретін болса, онда мембрананың ішкі және сырты ортадағы иондар концентрациясы теңесер еді, бұл жасуша үшін өте қауіпті жағдай, сондықтан орталардағы иондардың концентрацияларын әр түрлі болуын қамтамасыз ететін механизм де болуы тиіс. Ол активті тасымалдау нәтижесінде іске асады және заттар концентрациясы аз ортадан концентрациясы көп ортаға қарай, яғни градиентке қарсы бағытта тасымалданады, әрине мұндай тасымалдануға энергия қажет. Осы мақсаттағы энергия көзі болып аденозин трифосфат қышқылы молекуласының (АТФ) ыдырау кезінде бөлінетін энергиясы қолданылады (5 сурет) .

3 Na ⁺

2 K ⁺

3 Na ⁺ 2 K ⁺

5 сурет

Ғылыми тәжірибе негізінде АТФ бір молекуласы ыдырағанда бөлінетін энергия арқылы сыртқы ортаға 3 натрии ионын, ішкі ортаға 2 калии ионын тасымалдауға жететіндігін көрсетті. Тасымалдағыш ақуыз АТФ молекуласынан бөлінген энергияның есебінен бір жағымен сыртқы ортадан 2 калии ионын, ішкі ортадан 3 натрии ионын қосып алып, мембрана қабатында 180 ⁰ бұрылып, натрии ионын сыртқы ортаға, калии ионын ішкі ортаға жеткізеді, онан соң ақуыз қайта өз орнына келеді.

АТФ энергиясы арқылы зат тасымалдайтын осындай ақуыздарды иондық насостар деп атайды. Қазіргі кезде толық зерттелген осындай үш түрлі электрогенды насостар белгілі, олар: калии-натрии насосы (3 натрии ионын сыртқа, 2 кали ионын ішке), кальции насосы (2 кальци ионын сыртқа) және протон насосы (2 протонды сыртқа)

Осындай тасымалдау арқылы жасуша ішкі ортада калий ионының концентрациясын жоғары деңгейде, ал натрии ионынын төмен деңгейде ұстап тұрады. Активті тасымалдау кезінде мембрананың талғампаздық (селективті) қасиеті сақталады.

Заттар мембранадағы иондық каналдар арқылы да тасымалданады. Мембрана қабатындағы орналасқан ақуыз молекулалары мен липидтер саңлаулар (пор), яғни иондық каналдар жасайды. Мұндай индық каналдар арқылы мембранаға су молекулалары мен ірі иондар тасымалданады. Каналдар мембрананың өткізгіштік коэффициентін жоғарылатады, канал көп және олардың радиустары үлкен болған сайын мембрананың өткізгіштігі де артады. Каналдардың тасымалданатын заттарды таңдап өткізетін қасиеті бар. Әр иондық канал өзіне тиісті ғана ионды немесе затты өткізеді, яғни натрии каналы негізінен натрий ионын, калий каналы тек калии иондарын өткізеді. Сонымен қатар каналдардың заттарды өткізуі олардың зарядына байланысты болады, мысалы катиондарды өткізетін канал аниондарды өткізбейді, керісінше аниондарды өткізетін канал катионды өткізбейді. Каналдар өзіне тән емес иондарды да өткізеді, бірақ ол заттар үшін каналдың өткізгіштігі өте төмен, мысалы натрии каналының калии ионын өткізуі натримен салыстырғанда 20 есе төмен.

Мембранадағы каналдарды кейбір қосылыстар арқылы жауап тастауға болады екен, мысалы тетродотоксин молекуласы натрии каналын, тетраэтиламония молекуласымен калии каналын жауап тастайды. Мұндай әдістер медицинада көп қолданылады, мысалы ота жасағанда, тіс жұлғанда қажетті аймақты жансыздандыру осы құбылыстардың арқасында орындалады.

1842 жылы Э. В. Брюкке қуық қалтасындағы суды тасымаладауды зерттеу нәтижесінде тірі ағза ұлпаларында зат тасымалы саңлаулар (пор) арқылы жүретіндігін жобалаған болатын. Брюкктің бұл гипотезасы тек жүз жылдан кейін Ходжикин мен Хакслидің (1952), Девсон мен Даниеллидің (1955) ғылыми жұмыстары және Хладни мен Хайдонның(1970, 1972) жасанды липид биқабатына орнатылған грамицидитті(ақуыз) каналдың қасиетін зерттеулері нәтижесінде дәлелденді.

Қазіргі заманғы концепция бойынша мембранадағы иондық каналдар деп липид биқабатын тесіп орналасқан, электрохимиялық потенциалы аз жаққа қарай зат тасымалын қамтамасыз ететін интегралды ақуыздарды (олардың комплексін немесе гликопротеид) атайды. Иондық канал арқылы зат тасымылының өткізгіштік коэффициенті 10 ^-8 - 10 ^-9 м/с тең, бірақ бұл шама судағы еркін диффузия арқылы иондарды тасымалдаудан 5-6 есе төмен.

Хилле 1977-84 ж. ж. аралығында жүргізген зерттеулері нәтижесінде иондық каналдың мынадай моделін ұсынды: иондық каналда селективті сүзгі (фильтр) және «қақпа» тәрізді механизм бар. (6- сурет) .

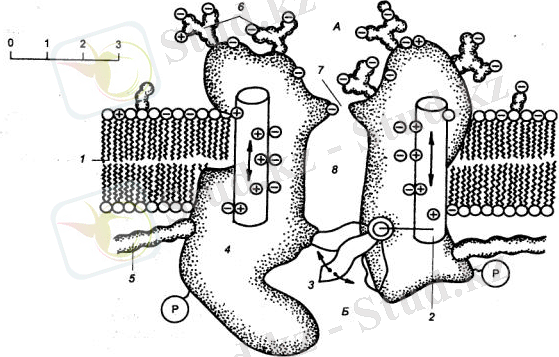
6 сурет. 1 - липидті биқабат, 2 - кернеу сенсоры, 3- қақпа,

4 - селективті фильтр 5- ақуыз макромолекуласы, 6-көмір сулар, 7- пор,

Селективті сүзгі канал арқылы тек белгілі бір заттарды өткізу немесе оларды басқалардан бөліп алумен айналысады. Бірақ мұндай ион каналының өлшемі (радиусы, кеңдігі) өзгермейді, мембрананың өткізгішті әр уақытта тұрақты, өзгеріссіз қалады.

Мембараның өткізгіштігі «қақпа» механизмі арқылы реттеледі. Иондық каналдың «қақпасы» ақуыз комплексінен құралады, «қақпаның сыртқы механохимиялық және т. б. әсерлерден «бұралатын» немесе «кері бұралатын» қасиеті бар, соның нәтижесінде ақуыз комплексінің саңлауы тарылады немесе кеңейеді, яғни «қақапының» өткізгіштігі өзгеріп тұрады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.