Ішкі тіректі,шоғырланған массалы айналу қабықшаның және серпімді пластинаның меншікті тербелістері

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ4

1 ТҰТҚЫРСЕРПІМДІ ЖҮЙЕДЕГІ СЫЗЫҚТЫҚ ТЕРБЕЛІСТІҢ ДЕМПФИРЛЕНУІ9

1. 1 Жалпылама ұғым мен негізгі арақатынастары9

1. 2 Меншікті және мәжбүрлі тербеліс есебінің қойылымы13

2 ІШКІ ТІРЕКТІ, ШОҒЫРЛАНҒАН МАССАЛЫ АЙНАЛУ ҚАБЫҚШАНЫҢ ЖӘНЕ СЕРПІМДІ ПЛАСТИНАНЫҢ МЕНШІКТІ ТЕРБЕЛІСТЕРІ18

2. 1. Нүктелік байланысты серпімді тікбұрышты пластинаның өзіндік тербеліс есебінің математикалық қойылымы18

2. 2. Нүктелік байланысты пластиналардың өзіндік тербеліс есебінің шешімі бар теңдеулерін құру21

2. 3. Нүктелік байланысты серпімді пластинаның өзіндік тербеліс есебіндегі әдістерде жинақтылығы тәжірибеде бағалануы25

2. 4. Айналу қабықшасы және айналу қабықшалар жүйесі әдістерін жалпылау29

2. 5. Серпімді есептерді шешу және талдау34

3 НҮКТЕЛІК БАЙЛАНЫСТЫ ҚҰРЛЫМЫ БІРТЕКТІ ЕМЕС ТҰТҚЫРСЕРПІМДІ МЕХАНИКАЛЫҚ ЖҮЙЕЛЕРДІҢ ӨЗІНДІК ТЕРБЕЛІСІ43

3. 1. Нүктелік байланысты құрлымы біртекті емес тұтқырсерпімді жүйелердің өзіндік тербеліс есебінің вариациялық қойылымы43

3. 2. Өзіндік тербелістің тұтқырсерпімді есебін шешудегі вариациялық әдіс алгоритмі. 48

3. 3. Құрлымы біртекті емес нүктелік байланысты тұтқырсерпімді жүйелердің өзіндік тербеліс есебін талдау және шешу50

4 ҚҰРЛЫМЫ БІРТЕКТІ ЕМЕС ТҰТҚЫРСЕРПІМДІ НҮКТЕЛІК БАЙЛАНЫСТЫ ЖҮЙЕЛЕРДІҢ ТҰРАҚТАЛҒАН СЫЗЫҚТЫ ТЕРБЕЛІСІ57

4. 1 Тұтқырсерпімді нүктелік байланысты жүйелердің мәжбүрлі тербеліс есебінің математикалық қойылымы. 57

4. 2 Тұтқырсерпімді нүктелік байланысты жүйелердің мәжбүрлі тербелісінің сызықты есебінің теідеулерінің шешу құрлымы. 59

4. 3. Тұрақталған тербеліс есебін шешу және талдаудың сандық алгоритмі. 61

ҚОРЫТЫНДЫ65

Пайдалынылған әдебиеттер тізімі66

КІРІСПЕ

Жұмыстың жалпы сипаттамасы

Магистрлік жұмыс вариациялық әдіс негізінде математикалық модельдеу әдісін дамытуға арналған. Сонымен қатар, серпімді және тұтқыр серпімді, пластиналық және қабықша жүйелердің нүктелік байланысы мен шоғырланңан массалары бар динамикалық есептер шешіміне және теориялық-зерттеушілік сипаттамаларға ие.

Зерттеу тақырыбының өзектілігі . Заманауи техникада пластиналар мен қабықшалар кеңінен қолданылуда. Олар, ережеге сәйкес, конструкция элементтері бола тұра, басқа элементтермен түйіндес немесе тіреу нүктелеріне ие, шоғырланған сипаттағы массаларды атқарады. Тіреу нүктелерінің, сонымен қатар, шоғырланған массалардың болуы елеулі түрде пластиналар мен қабықшалардың(өзіндік жиілігі және тербеліс формасы) динамикалық сипаттағы есептеуін қиындата түседі. Серпімді тікбұрышты пластиналар мен нүктелік байланысы бар айналмалы қабықшасының динамикалық өзгеруін есептейтін қолданыстағы әдістер, ережеге сәйкес, нақты есептерді шешуге бағытталған (шекаралық шарттары, нүктелік байланыстың саны мен түріне, олардың орналасуы және т. б. бойынша) . Серпімді динамикалық есептердің бүтін класына арналған бірыңғай әдісті құруды ұсыну маңызды. Полимерлі материалдардың кең қолданыста болуын, пластиналармен қабықшалардың тұтқырсерпімді жүйелерін модельдеудегі осы әдісті жинақтау қажеттілігімен түсіндіруге болады.

Диссертациялық жұмыстың мақсаты : Әмбебаптылыққа, салыстырмалы түрде қаралатын, жақсы жинақтылыққа ие, меншікті және мәжбүрлі сызықтық тербелістердің, серпімді және құрылымды біртексіз, тікбұрышты пластиналар мен нүктелік байланысы бар айналыу қабықшаларының тұтқырсерпімді жүйелері және шоғырланған массалары туралы есептердің алгоритмін құру.

Зерттеудің ғылыми жаңалығы . Серпімді тікбұрышты пластиналар үшін кинематикалық сипаттағы нүктелік байланыс пен шектеулерді есептеу тәсілі ұсынылады. Виртуалды орын ауысудың термин принциптеріндегі динамикалық сипаттағы пластиналарға көрсетілген байланыстардың әсер етуі Лагранж көбейткіштері әдісі арқылы зерттеледі. Классикалық жинақталған қойылымға меншіктік мәндер туралы туынды есебінің мәлімет әдісі көрсетілген. Әдістеме серпімді және құрылымды біртексіз тұтқырсерпімді тікбұрышты пластиналар жүйесі немесе нүктелік байланысы бар айналу қабықшалары және шоғырланған массалары жағдайында таратылған. Құрылымды біртексіз тұтқырсерпімді меншіктік және мәжбүрлі тербелістерге арналған бірнеше есептер шығарылады.

Зерттеу нәтижелерінің практикалық және теориялық маңыздылығы . Нүктелік байланыстары мен шоғырланған массалары бар пластинаның және қабықшалы конструкциялардың динамикалық есептеуге арналған алгоритм ДК ЭЕМ-ге арналған стандартты бағдарламалар үшін кеңінен қолданылады, сондықтан, ол инженер құрастырушыға ыңғайлы. Әдістің есептеу тиімділігі қанағаттанарлықтай нәтижелерде зерттеу және есептеу жұмыстарын жүргізуге мүмкіндік береді.

Математикалық модельдеу - бұл құбылыстарды зерттеу, процестерді, олардың модельдерін құрастыру және оқып үйрену жолы арқылы, жүйелер мен объектілерді соңғысының сипаттамасын анықтау немесе нақтылау үшін пайдалану және қайта құрастырылатын технологиялық процестерді, жүйелерді және объектілерді зерттеу. Математикалық модельдеу негізіне түпнұсқа мен модельдің айнымалы параметрлерінің біртектес немесе ұқсас теңдеулермен сипатталуы алынады. Математикалық модельдеу көбінесе компьютерлер арқылы зерттеледі, сондықтан оны кейде компютерлік модельдеу деп те атайды.

Математикалық модель - бұл шынайы әлемнің абстракциясы, мұндағы зерттеушіні қызықтыратын шынайы элементтер арасындағы қатынас сәйкесінше математикалық категориялар арасындағы қатынаспен алмастырылған. Бұл қатынастар, ережеге сәйкес, модельдеуші шынайы жүйенің жұмыс істеуін сипаттайтын теңдеу немесе теңсіздік түрінде көрсетілген. Математикалық модель құру өнері, математикалық сират тұрғысындағы неғұрлым ықшамдылықты зерттеушіні қызықтыратын шынайылықтың дәл сол тұстарын жеткілікті модельдік дәлдікпен жаңадан өндіріп, қиылыстыру болып табылады.

Аналитикалық, имитациялық, сандық, функционалдық және матрицалық математикалық модельдер белгілі. Аталған модельдердің кез-келгені төмендегідей классификациялануы мүмкін:

уақыт тәртібі бойынша (динамикалық, статикалық, квазистатикалық) ;
кіру ақпаратының түрі бойынша (детерминдендірілген, стахастикалық, үздіксіз, дискреттік) ;
математикалық аппараттың қолданылу түрі бойынша (сызықтық, сызықтық емес, оптимизациялық, оптимизациялық емес) .

Нақтылығы - сандық әдіс бойынша негізделген ақиқаттың бар болу формасы, мысалы, тәжірибе арқылы, субъектіні тану үшін логикалық дәлелдеу. Математикалық модельдеудегі нәтижелердің нақтылығы - модель тиімділігінің негізгі көрсеткіші. Модельдеу нәтижелерінің нақтылығын бағалау процедурасының өзін, оның модельдеуші объектіге, жүйеге және процесске модельдің баламалығының анализі деп атайды.

Қазіргі таңда көптеген техникалық конструкцияларда қабықшалы және пластина түріндегі конструкциялар кеңінен қолданылуда [1, 2, 3, 4] . Жұқа қабатты трубалар мен панелдер шынайы жағдайларда, ережеге сәйкес басқа конструкциялар және денелермен өзара әрекеттеседі, нүктелік қатты және(немесе) серпімді, шарнирлік және(немесе) қысылған тіректерге тіреледі және нүктелік жалғасқан массалары бар [6, 7] . Шекаралық шарттары біркелкі шарттардан жиі ерекшеленеді. Егер статикалық нүктелерде бұл ерекшеліктер деформация мен кернеу өзгерістерінде локальді қайта орналастыруды туғызса, онда динамикалық есептерде нүктелік байланыстар пластиналардың барлық диннамикалық сипаттамаларына немесе қабықшаларға - өзіндік спектр жиілігіне, өзіндік тербеліс формасына, резонансты жиілікпен амплитудаға және т. б. тікелей әсер етеді. Соңғы кездері, әсіресе виброқорғаныс жүйелерінде өте өзекті болып жатқан, егер пластина мен қабықша мұрагерлік қасиеттерге ие болса, онда есеп күрделене түседі [8, 9, 10] . Көрсетілген есептер класының динамикасына байланысты көптеген басылымдар пластиналар мен нүктелік байланысы бар қабықшалардың динамикалық тәртібінің серпімді есебіне арналған [11, 12] .

Ішкі нүктелерге тірелген және жинақталған жүгі бар пластиналар мен басқа да конфигурацияларға (трапеция, шеңбер және т. б. ) арналған бірқатар динамикалық есептеулер бар [13, 14] . Өзіндік жиілік пен формаларды алу үшін негізінен диференциалдық тәсіл пайдаланылады.

Серпімді қабықшалардың өзіндік тербелісі бойынша жұмыс анализі [15, 16, 17], жоғарыда сипатталған барлық нүктелік байланыс түрі бар қабықшалы конструкциялардың динамикалық есептеу әдістерінің айтарлықтай жетілдірілгендігін көрстеді.

Диссипатиялық қасиеттері бар жүйелерге арналған динамикалық есептер де үлкен қызығушылық тудыруда [18, 19] .

Әрі қарай құрылымдық біркелкі емес тұтқырсерпімді жүйелерді әртүрлі геологиялық қасиеттері бар элементтерді механикалық жүйелер деп атаймыз [19, 20] . Ғылыми әдебиеттерде проблемаларды барлық жағынан алып қарағанда, еркін дәрежелі соңғы сандары бар динамикалық тұтқырсерпімді жүйелердің сөнуін пайдалану сұрақтары сирек қарастырылады [21, 22] . Сонда да, екі серпімді тіректердегі қатты дене түріндегі объектіні қорғау есептері инженерлік тәжірибе үшін маңызы зор, өйткені, «балдық» түрдегі жүйелер тасымалдаушы динамикада кеңінен қолданылады [23, 24, 25, 26] .

Бірінші тарауда өзіндік және мәжбүрлі тербелісті есептердің қойылуы сипатталады. Тек қана қатты денелерден тұратын, бір-бірімен өзара массасыз тұтқырсерпімді элементтерімен байланстырылған механикалық жүйелердің тербелісі қарастырылады.

Екінші тарауда өзіндік тербелістердің серпімді есебі қарастырылады. Тікбұрышты пластиналарды Гамильтон - Остроградский принципі бойынша варияциялық теңдеуі алынып, варияциялық қойылым ұсынылады. Серпімді тіректермен шоғырланған массалар, тіректің және варияциялық теңдеулердің потенциалды және кинетикалық энергияларды ендірумен есептеледі.

Ритц әдісі арқылы варияциялық теңдеуді шешу, пластинаның геометриялық шеттік нүктелік емес байланысын қанағаттандыратын базисті функциялық класта орналастырылған. Алынған сызықты біртекті теңдеулер жүйесі өзіндік мәнін табуға арналған есеп болып табылады, оны шығаруға болмайды, өйткені, массалардың жалпылама матрицасы, көп жағдайларда массалардың жалпылама қатаңдығы, жұмсалған нүктелік байланыстар арқылы туындайды. Туынды емес қайта келтіруден (Гаусс әдісі) сызықты тәуелді жалпылама кординаталар алынып тасталады және жүйе есептеуге болатын дәстүрлі өз мәндері бар жалпылама есепке келтіріледі.

Нәтижелері бар сандық тәжірибелер және салыстырулар әдістің қанағаттанарлық сәйкестігін көрсетеді.

Әдіс қатты тіректермен, серіппелермен байланысқан және нүктелік тірек пен жинақталған массалары бар тікбұрышты пластиналар жүйелері үшін де жалпыланған. Оның айналу қабықшасы мен айналу қабықшасының жүйесіне таратылуы варияциялық тәсіл шеңберінде де келтірілген, бірақ орын ауысу мүмкіндігі бар принцип терминдерінде бірқатар серпімді есептер шешілді. Пластиналарды қосатын, екі квадрат пластинаның серіппелерінің қатаңдығына қарай, пакеттің өзіндік формасы мен жиілігінің өзгеруіне талдау жасалды. Мысалдарда тікбұрышты пластиналардың үзілісті шекаралық шарттарының нүктелік апроксимациялануының қанағаттанарлық мүмкіндіктері берілген. Бұл қазіргі таңдағы аз зерттелген есептерді зерттеуге мүмкіндік береді, оның ішінде, ішкі нүктелерде тірелген және контурында шекаралық шарттары бар тікбұрышты пластинаның өзіндік тербелісінің формасы мен жиілігін аныч(қтауға мүмкіндік бар.

Үшінші тарау нүктелік байланыстары бар құрлымы біртекті емес тұтқырсерпімді жүйелердің өзіндік тербелістеріне арналған. Өзара серпімді немесе тұтқырсерпімді байланысқан (серіппелер, амортизаторлар) тұтқырсерпімді пластиналардың немесе коаксиалды орналасқан айналу қабықшаларының пакеті қарастырылады. Тұтқырсерпімді элементтерінің өзгерісі ерекшеленген параметрлері бар мұрагерлік түйіндері арқылы сипатталады. Мұндай жүйенің вариациялық қойылымдағы, орын ауысу мүмкіндігінің принциптері негізіндегі өзіндік жиілік пен демпфирлену коэффициенті зерттеледі. Варияциялық есептегі серпімділігінің тұрақты шамасы интегралды операторлар арқылы ауыстырылады. Шешімді серпімді есептің аналогиясы бойынша іздейміз. Қатыру әдісінің көмегімен интегралды теңдеулер жүйесі алгебралық сызықтық біртекті комплекстік теңдеулер жүйесіне келтіріледі. Жиіліктік теңдеуінің өзіндік жиілігі мен демпфирлену коэффицентін іздеу жүйе анықтауышын ашпай Мюллер әдісі арқылы іске асырылады. Бірқатар есептердің нәтижелерінің қортындысы пластиналар мен айналу қабықшалардан құралған құрлымдық біртекті емес тұтқырсерпімді жүйелердің өзара сөнуі кезінде пайда болатын өзіндік формалардың өзара әсерлесу эффектісі байқалатындығын көрсетті. Бұл эффектінің пайда болу шарттары анықталды, амортизаторлардың мезеттік қатаңдылығының өзгеруінде демпфирлену коэффиценттерінің графигінде жүйенің алғашқы екі формасы қиылысады, ал қиылысу нүктесіндегі энергияның диссипациясы жүйеде максималды. Сонымен қатар, құрылымдық біртекті емес тұтқырсерпімді жүйенің демфирлену коэффицентін анықтайтын, оның өзіндік жиілік спектрінде айтарлықтай өзгермеген геометриялық параметрлердің (массаның, амортизаторлардың орналасуы, т. б. ) маңызды тәуелділік эффектісі анықталады.

Төртінші тарауда варияциялық тәсілмен құрастырылған сызықтық тербелістердің есептері шешілді. Алдыңғы тараудан ерекшелігі варияциялық теңдеуге гармоникалық заңы бойынша өзгеретін жоғарғы күштердің виртуалды жұмысы қосылған. Шешімді сонымен қатар, нүктелік байланысы жоқ пластиналардың (қабықшалардың) гармоникалық шектік шарттарын қанағаттандыратын функциялар класынан іздейтін боламыз. Сызықтық біртекті емес теңдеулер жүйесі Гаусс әдісі бойынша негізгі элементті матрицаның бағаны мен қатарынан белгілеу арқылы шығарылады. Кейбір нақты есептер үшін амплитудалы - жиіліктік сипаттамалар алынды. Олар алдыңғы тараудағы анықталған механикалық эффектілердің барын растайды. Зерттеу нәрсесі ретінде түгелдей тұтқыр сұйықтықпен толтырылған немесе оған батырылған, сондай-ақ, скважиналардағы мінсіз сұйықтықпен толтырылған түзу және қисық сызықты трубалардағы динамикалық процестер болып табылады. Деформацияланатын динамикалы серпімді денелердің есептері ғалымдардың назарын аударуда. Бұл маңызды қолданбалы шешу қажеттілігімен түсіндіріледі. Машина жасау және құрылыс салаларының заманға сай дамуы конструкциялардың әртүрлі динамикалық әсер ету түрлеріндегі кернеулі-деформациялану жағдайларын дәл білуді қажет етеді. Жаңа техниканың түрлі салаларындағы өнім мен нысандарды жобалауда, сонымен қатар, сейсмотұрақтылық есептеріне байланысты конструкцияға қоршаған ортаның әсер етуі есебінің қажеттілігі туындайды. Басқа жағынан қарағанда, мұндай модельдер мысалы, шөгінді түрлерінде кездесетін сейсмология мен сейсмабарлаудың қабаттық құрылымдарында баламалы болып табылады.

1 ТҰТҚЫРСЕРПІМДІ ЖҮЙЕДЕГІ СЫЗЫҚТЫҚ ТЕРБЕЛІСТІҢ ДЕМПФИРЛЕНУІ

Бұл бөлімде диссапативті механикалық жүйенің негізгі қатынасы жәнекейбір жаңа түсініктер келтірілген.

1. 1 Жалпылама ұғым мен негізгі арақатынастары

Мұнда S денеден (S _к - қатты, S _е - тұтқырсерпімді; 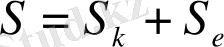) тұратын механикалық жүйенің өзіндік тербелісі қарастырылады. Денелер жүйесі бір-бірімен және массасыз (немесе массалық негізде) тұтқырсерпімді элементтермен байланысқан. Материалдардың тұтқырсерпімді құрамы Больцман-Вольтердің интегралдық [14, 18] . Деформацияланған элементтердің кейбірісерпімді болуы мүмкін, элементтердің реологиялық құрамын сипаттайтын жағдайда мұрагерлік ядросы нөлге тең. Деформацияланған элементтердің реологиялық құрамы бірдей жүйені (элементтердің мұрагерлік ядросы өзара тең) диссипативті біртекті, ал деформацияланған элементтердің реологиялық құрамы әр түрлі жүйені - диссипативті біртексіз деп атаймыз [15] .

Жұмыстың негізгі мақсаты - нүктелік тіреуі және шоғырланған массалары бар пластиналық жүйенің диссипативті (демпфирленетін) құрамын зерттеу болып табылады. Еркін тербелістерде сөну жылдамдығы жүйенің диссипативті құрамымен сандық бағаланады: жылдамдық неғұрлым жоғары болса, диссипация да соғұрлым жоғары. Жүйенің диссипативті құрамын сандық бағалау үшін екі шама ұсынылады, олар: меншік тербелісінің минималды сөну жылдамдығы мен максималды резонансты амплитуда. Жүйенің диссипативті құрамы, ең алдымен элементтердің демпфирленусипаты арқылы анықталады [29] . Бұл пайымдау диссипативті біртекті жүйелерге бұл таптырмас тұжырым болса, ал диссипативті біртексіз жүйелерге мүлдем қолдануға келмейтін тұжырым. Демпфмирленудің глобальдық коэффиценті ұғымы енгізілді. Ол үшін демпфирленудің глобальды демпфмирлену сипаттауыш сін серпімді құрамды элементтермен ғана анықталмайды, сонымен қатар, әр түрлі формадағы тербеліс байланысымен, яғни, құрамы, конструкциясы, геометриясымен, жұмсақтық байланысымен, өлшемімен, орналасқан элементтері арқылы анықталады [30, 31, 32] .

Комплексті меншік жиілігі 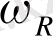сөну тербеліс жиілігіне тең, жалған 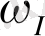- демпфирленудің меншік тербеліс коэффициенті. Меншік және еріксіз тербеліс тапсырмасын орындау барысында, мүмкін болатын орын ауыстырулар принципі пайдаланылады (мұнда жалпы белсенді күштер сомасы, инерция күшін қоса есептегенде нөлге тең) [32] .

1. 1. суретте көрсетілгендей диссипативті біртексіз механикалық конструкция РЭА жүйесінің динамикалық коэффициент анализін жүргізейік.

сурет. Екі дәрежелі еркіндік жүйесі

1. 1. суретте 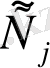- серіппе қаттылық операторы, ол (j=1, 2, 3) мынадай түрде көрсетілген [15] :

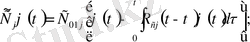(1. 1)

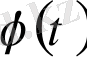- уақыт функциясы; 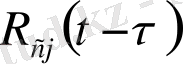- релаксация ядросы. Әрі қарай тоңазыту рәсімін қолдана отырып [30] арақатынасты былайша түрлендіреміз (5)

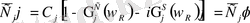Мұнда 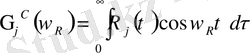, , 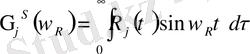сәйкесінше косинус пен синус - релаксация материалының Фурье ядросы образы. Жұмсақ материал мысалы ретінде үшпараметрлі ядро релаксациясын 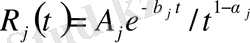қарастырайық (бұл мысалда ядро әлсіз сингулярлы) [29] .

Мысал ретінде еріксіз жұмсақ жүйенің шектік санды еркіндік тербелісін қарастырайық. Кеңістікте $q_{i}(i = 1, \ldots, n)$ координатасымен жинақталған сызықтық тербеліс жүйесі берілген. Жүйеге жинақталған екі типті жинақтық күші әсер етеді деп болжануда. Біріншіден, бұл күштер жинақтық кординаталарына сызықты тәуелді, бұл тәуелділік мұралық сипаттауыш мен түсіндіріледі:

${\overline{Q}}_{i}(t) = \sum_{j = 1}^{n}\left\lbrack C_{ij}q_{j}(t) - \int_{- \infty}^{t}{R_{ij}(t - s) q_{j}(s) ds} \right\rbrack$

Мұнда ${\overline{Q}}_{i}$ -мұралық жинақтық типті күштер; $C_{ij}$ - сондай белгілі константалар, квадрат формасы

$\sum_{j = 1}^{n}{C_{ij}q_{i}q_{j}}$

оң анықталған, ал $R_{ij}$ - белгілі ықпалдық функциясы. Екіншіден, уақытқа тәуелді жинақтық күштермен түсіндіріледі және осы тәуелділік гармоникалық. Сызықтық күш тапсырма жағдайын қарастырғанда нақты уақытқа тәуелді жинақтық күштер теңдей фаза мен кезеңдерді құрайды:

$Q_{i}(t) = Q_{i0}sinpt\ \ \ \ (i = 1, \ldots, n)$ ( 1. 2)

Қарастырылып отырған жүйе үшін (1. 1) Лагранж көбейткіші былайша түрленеді:

$\sum_{j = 1}^{n}\left\lbrack a_{ij}{\ddot{q}}_{j} + C_{ij}q_{j}(t) - \int_{- \infty}^{t}{R_{ij}(t - s) q_{j}(s) ds} \right\rbrack = Q_{i0}sinpt.$ (1. 3)

Мұнда коэффициенттер оң белгілі квадрат формада

$\frac{1}{2}\sum_{i, j = 1}^{n}{a_{ij}q_{i}q_{j}}.$

Тапсырмада жүйенің периодты шешімін табу (1. 3) керек. (1. 3) жүйені $R_{ij} = 0$ болғанда, бірқалыпты серпімді жүйе координатына келтіреміз. Оны былайша түрлендіреміз:

$q_{j} = \sum_{k = 1}^{n}b_{ik}\Theta_{k},$

$\Theta_{k}$ - бірқалыпты координаттар, $b_{jk}$ - матрица түрленуінің коэффициенті, мұнда $\det\left\lbrack b_{jk} \right\rbrack \neq 0$ тең. $\Theta_{k}$ координатасында (1. 3) жүйе былайша өрнектеледі

${\ddot{\Theta}}_{i} + \omega_{i}^{2}\Theta_{i} - \int_{- \infty}^{t}{\sum_{k = 1}^{n}{{\overline{R}}_{ik}(t - s) \Theta_{k}(s) ds}} = Q_{i0}sinpt\ \ \ (i = 1, \ldots, n),$ (1. 4)

$\omega_{i}$ - серпімді жүйенің меншік жиілігі, $\Theta_{0i}$ - жинақталған күштердің амплитудасы, сәйкесінше бірқалыпты координаттар арақатынасы былайша анықталады

$\Theta_{0i} = \sum_{k = 1}^{n}b_{ki}\Theta_{0k},$

Мұнда ${\overline{R}}_{ik}$ - әсер ету функциясы:

${\overline{R}}_{ik} = \sum_{j = 1}^{n}R_{ij}b_{jk}.$

(1. 3 ) жүйенің периодтық шешімін мына түрде анықтаймыз

$\Theta_{i}(t) = A_{0i}\sin\left( pt + \varphi_{i} \right),$ (1. 5)

Мұнда $A_{0i}, \ \varphi_{i}$ - константалар, трансцендентті жүйе теңдеулерімен анықталады.

$\left( \omega_{i}^{2} - p^{2} \right) A_{0i}\cos\varphi_{i} - \sum_{k = 1}^{n}{\left( U_{cik}\cos\varphi_{k} + U_{sik}\sin\varphi_{k} \right) A_{0k}} = \Theta_{0i},$

$\left( \omega_{i}^{2} - p^{2} \right) A_{0i}\sin\varphi_{i} - \sum_{k = 1}^{n}{\left( U_{cik}\sin\varphi_{k} + U_{sik}\cos\varphi_{k} \right) A_{0k}} = \Theta_{0i}$ (1. 6)