Комплекс сандар: анықтамасы, амалдары, тригонометриялық түрі және n-ші дәрежелі түбірлер


Н. Нұрмақов атындағы №2 мамандандырылған облыстық
дарынды балалар мектеп-интернаты
КОМПЛЕКС САНДАР ұғымы
(мектепішілік ғылыми-практикалық конференцияға ұсынылады. )
Орындаған: 8-сынып оқушысы Айтжан Темирлан
Қарағанды қаласы - 2010 ж.
КОМПЛЕКС САНДАР.
Комплекс сандар алгебралық теңдеулерді шешу негізінде пайда болды.
Комплекс сан деп z=a+bi түріндегі санды айтамыз, мұндағы a және b -нақты сандар, ал i -жорамал бірлік, i 2 =-1. a комплекс санның нақты бөлігі, b -оның жорамал бөлігі. Re(z) = a, Im(z) = b
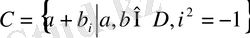 - комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі,
- комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі,
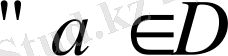 үшін
үшін
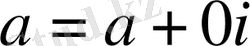 .
.
Комплекс сандар жиыны нақты сандар жиынының кеңеюі
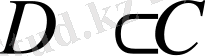 .
.
z=
a+bi
және
 =
a-bi
өзара
түйіндес сандар
деп аталады
=
a-bi
өзара
түйіндес сандар
деп аталады
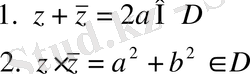
z
1
=
a+bi
және z
2
=
c+di
cандары тең

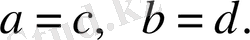
Комплекс сандарының қосындысы комплекс сан болады.
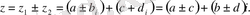
Қосудың қасиеттері:
∀z 1 , z 2 , z 3 ∈C үшін (z 1 +z 2 ) +z 3 =z 1 +(z 2 +z 3 ),
∃0∈C, ∀z∈C, z+0=0+z=z,
∀z∈C, ∃ -z∈C, z+(-z) =(-z) +z=0,
∀z 1 , z 2 ∈C; z 1 +z 2 =z 2 +z 1 .
Комплек сандардың көбейтіндісі комплекс сан.
z=z 1 ⋅z 2 =(a+bi) ⋅(c+di) =(ac-bd) +(bc+ad) i.
Көбейтудің қасиеттері:
∀z 1 , z 2 , z 3 ∈C (z 1 ⋅z 2 ) ⋅z 3 =z 1 ⋅(z 2 ⋅z 3 ) (ассоциативті),
∃1∈C, ∀z∈C, z⋅1=1⋅z=z (1=1+0⋅ i ),
∀z∈C, ∃ z -1 ∈C, z⋅z -1 =z -1 ⋅z=1 (z= a+bi және z -1 = 1/z=( a/(a 2 +b 2 ) ) +((- b ) /( a 2 +b 2 ) ) i ),
∀z 1 , z 2 ∈C, z 1 ⋅z 2 =z 2 ⋅z 1 (коммутативті) .
Қосу мен көбейту амалдары дистрибутивтілік заңымен байланысқан
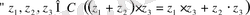 Equation. 3 .
Equation. 3 .
Комплекс сандардың бөліндісі комплекс сан,
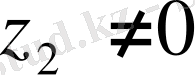
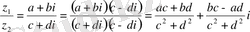
Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.
Комплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. O
x -
осінің бойына комплекс санның нақты бөлігін
(a=a
+0∙
i),
ал O
y
осінің бойына оның жорамал бөлігін орналастырсақ (
bi=0+bi)
жазықтықта әрбір комплекс сан z(
a, b
) нүктесі түрінде анықталады.
 тік бұрышты
тік бұрышты
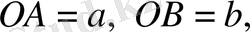 z
z
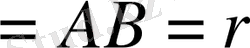 Equation. 3
r
=z=
Equation. 3
r
=z=
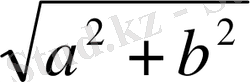 .
.
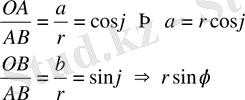
z= a+bi=r( cosφ+isinφ) - комплекс санның тригонометриялық түрі.
 =r - комплекс санның модулі
=r - комплекс санның модулі
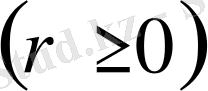 .
.
 -комплекс санның аргументі.
-комплекс санның аргументі.
Тригонометриялық түрдегі комплекс сандарға амалдар қолдану өте жеңіл.
Айталық,
z 1 = r 1 (cosφ 1 +isinφ 1 ),
z 2 = r 2 (cosφ 2 +isinφ 2 ) болсын.
Онда
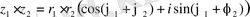
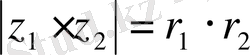
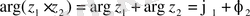
Егер
 болса, онда
болса, онда
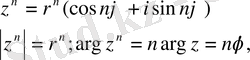
Муавр формуласы
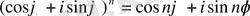
Комплекс саннан n ші дәрежелі түбір табу және 1 ден табылған түбірлердің группасы.
Айталық,
а=r(cos
 +isin
+isin
 )
комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін
)
комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін

яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.
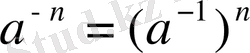
теңдігін пайдаланып, Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады.
a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек
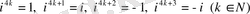
ескерсек жеткілікті.

Муавр формуласының дербес түрін қарастырайық.
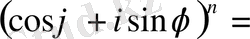 cos n
cos n
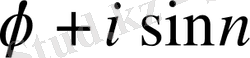

Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық.
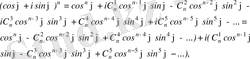
Мұндағы
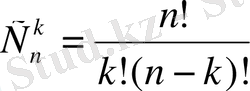
теңдігінің сол және оң жақ бөліктерін салыстырсақ,
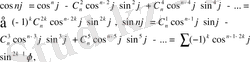
теңдіктерін аламыз.
Сонымен,
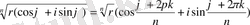 , мұндағы
, мұндағы
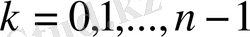
ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз.
Қортынды. Комплекс сандардан n - ші дәрежелі түбірді әрқашан табуға болады және оның әртүрлі n мәні болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz