Гиперболалық типтегі теңдеулердің бір класына арналған шешімдердің тегістігі мен аппроксимативтік қасиеттері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 56 бет
Таңдаулыға:
Мазмұны
Кіріспе
І. Функционалдық анализдің негізгі ұғымдары
1. 1. Сызықты және нормаланған кеңістік
1. 2. Гильберт кеңістігі,
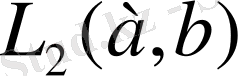 кеңістігі
кеңістігі
1. 3. Сызықты операторлар теориясының элементтері
1. 4. Сызықты оператордың ядросы, образы, рангі
1. 5. Кері оператор, сызықты оператордың спектрі
ІІ. Математикалық физиканың теңдеулері мен шешу әдістері
2. 1. Дербес туындылы дифференциалдық теңдеудің классификациясы
2. 2. Гиперболалық түрдегі теңдеулерге келтірілетін есептер
2. 3. Фурье әдісі(айнымалыларды ажырату әдісі)
ІІІ. Гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің тегістігі мен аппроксимативтік қасиеттерін зерттеу
3. 1. Гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің тегістігі
3. 2. Гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің апроксимативтік қасиеттері
Қорытынды
Пайдаланған әдебиеттер
КІРІСПЕ
Тақырыптың өзектілігі. Математикалық физиканың көптеген сұрақтары дифференциалдық операторлардың меншікті мәндері мен меншікті функцияларын анықтауға және кез келген функцияны меншікті функциясы бойынша қатарға жіктеуге алып келеді.
Гиперболалық түрдегі теңдеулер шектің тербеліс теңдеуін, толқындық теңдеулерді және т. с. с. процестерді сипаттайды.
Гиперболалық типті дербес туындылы дифференциалдық операторлар теорясындағы физикалық есептерді шешу кезінде екінші ретті дифференциалдық теңдеу маңызды орын алады.
Гиперболалық түрдегі теңдеулер үшiн қойылған есептердiң шешiмiн табу үшiн әртүрлi әдiстер қолданылады. Олардың iшiнде жиi қолданылатыны априорлы бағалау әдiсi, Фурье әдiсi т. б.
Гиперболалық теңдеудің зерттеу кезіндегі жекелеген нәтижелерді жүйелендіру және гиперболалық теңдеулердің жалпы теориясын құру Ж. Б. Фурье, О-Л. Коши, С. В. Ковалевская, Г. Дарбу, Э. Гурса, Б. Риман, П. -Г. -Л. Дирихле, Ж. Адамардың жұмыстарынан бастау алды.
Гиперболалық түрдегі теңдеулердің қасиеттері Мұратбеков М. Б., Мұратбеков М. М., Ахметжанов М. А., Жүсіпназаров Р. М. жұмыстарында қарастырылған.
Гиперболалық типті дифференциалдық теңдеулер үшін көптеген сұрақтар, яғни спектральдік қасиеттері арнайы зерттеуді қажет етеді.
Жұмыстың мақсаты. Жұмыстың негізгі мақсаты гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің тегістігі мен аппроксимативтік қасиеттерін зерттеу.
Зерттеу әдістемесі. Гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің тегістігі мен аппроксимативтік қасиеттерін зерттеу барысында төмендегідей әдістер пайдаланылды: априорлы бағалау әдісі және М. Б. Мұратбеков пен М. Өтелбаевтың жұмыстарында ұсынылған әдістер қолданылды.
Ғылыми жаңашылдығы. Жұмыста төмендегідей жаңа нәтижелер алынды:
1.
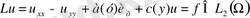 гиперболалық түрдегі теңдеулер үшін шешімнің тегістігі.
гиперболалық түрдегі теңдеулер үшін шешімнің тегістігі.
2. Жоғарыда көрсетілген оператор үшін Шмидт бойынша меншікті мәндерінің екі жақты бағалары алынды. (
 -сандары) .
-сандары) .
Теориялық және практикалық құндылығы. Кванттық физикада, дифференциялды операторлардың спектральді теориясында, жоғары курс студенттеріне арнайы курс оқу барысында қолданылатын нәтижелер алынды. Жұмыста алынған нәтижелерді семинарларда пайдалануға болады.
Жұмыстың апробациясы. Диссертациялық жұмыс сұрақтары «Қазақстан Республикасындағы білім мен ғылым интеграциясы проблемалары мен болашағы» атты Республикалық ғылыми-практикалық конференцияда және ф-м. ғ. докторы, профессор М. Б Мұратбековтың семинарларында талқыланды.
Диссертация құрылымы. Қарастырылып отырған жұмыс кіріспе, үш бөлім, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспеде тақырыптың өзектілігі, жұмыстың ғылыми жаңашылдығы мен теориялық және практикалық құндылығы айқындалған.
Бірінші бөлімде функционалдық анализдің негізгі ұғымдары мен анықтамалары қарастырылған.
Екінші бөлімде математикалық физиканың теңдеулері қарастырылып, оларды шешу әдістері туралы бірқатар мағлұматтар берілген.
Үшінші бөлімде гиперболалық түрдегі теңдеулердің бір класы үшін шешімнің тегістігі мен аппроксимативтік қасиеттері көрсетілген.
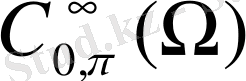 жиынында анықталған гиперболалық түрдегі дифференциалдық оперторады қарастырайық:
жиынында анықталған гиперболалық түрдегі дифференциалдық оперторады қарастырайық:
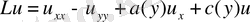
мұндағы
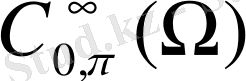 - шексіз дифференциалданатын, у айнымалысы бойынша финитті және келесі шарттарды қанағаттандыратын функциялар жиыны:
- шексіз дифференциалданатын, у айнымалысы бойынша финитті және келесі шарттарды қанағаттандыратын функциялар жиыны:
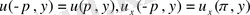
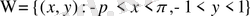 -тіктөртбұрыш
-тіктөртбұрыш
Келесі шарт орындалсын:
 және [-1, 1] кесіндісінде үзіліссіз функциялар .
және [-1, 1] кесіндісінде үзіліссіз функциялар .
Теорема1
. Айталық
 шарты орындалсын. Онда
шарты орындалсын. Онда
 болғанда
болғанда
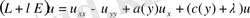 операторы үзіліссіз қайтарымды болады.
операторы үзіліссіз қайтарымды болады.
 функциясының тасымалдаушысы деп
функциясының тасымалдаушысы деп
 жиынында анықталған
жиынында анықталған
 жиынын айтамыз және
жиынын айтамыз және
 деп белгілейміз.
деп белгілейміз.
 жиынында үзіліссіз және
жиынында үзіліссіз және
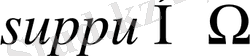 болатын функциялар финитті функциялар деп аталады.
болатын функциялар финитті функциялар деп аталады.
Анықтама 1.
Егер
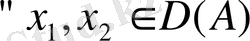 үшін
үшін
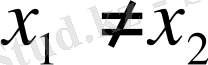 өрнегінен
өрнегінен
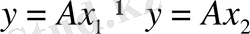 теңдігін алсақ, онда
теңдігін алсақ, онда
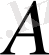 операторы өзара бірмәнді оператор деп аталады.
операторы өзара бірмәнді оператор деп аталады.
Анықтама 2.
Егер
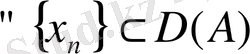 тізбегі үшін
тізбегі үшін
 және
және
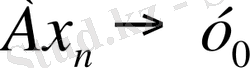 өрнегінен
өрнегінен
 және
және
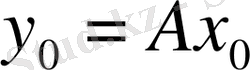 екендігі белгілі болса, онда
екендігі белгілі болса, онда
 операторы тұйық деп аталады.
операторы тұйық деп аталады.
Осы анықтамадан тікелей шығатыны : егер
 операторы тұйық емес болса, онда оны тұйықтауға болады. Бұл операция
операторы тұйық емес болса, онда оны тұйықтауға болады. Бұл операция
 операторының тұйықталуы, ал оператордың өзі тұйықталған болады.
операторының тұйықталуы, ал оператордың өзі тұйықталған болады.
Айталық
 және
және
 - нормаланған кеңістіктер болсын және
- нормаланған кеңістіктер болсын және
 кеңістігін
кеңістігін
 кеңістігіне бейнелейтін
кеңістігіне бейнелейтін
 операторын қарастырайық.
операторын қарастырайық.
 функционалын келесі формуламен анықтайық:
функционалын келесі формуламен анықтайық:
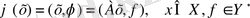 (3. 1. 5)
(3. 1. 5)
 кеңістігі -
кеңістігі -
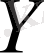 кеңістігіне түйіндес кеңістік. (3. 1. 5) формуласы бойынша әрбір
кеңістігіне түйіндес кеңістік. (3. 1. 5) формуласы бойынша әрбір
 элементіне
элементіне
 саны сәйкес қойылған,
саны сәйкес қойылған,
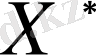 кеңістігі -
кеңістігі -
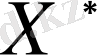 кеңістігіне түйіндес кеңістік.
кеңістігіне түйіндес кеңістік.
Осылайша
 сызықты үзілісіз операторын анықтадық.
сызықты үзілісіз операторын анықтадық.
 операторы
операторы
 операторына түйіндес деп аталады.
операторына түйіндес деп аталады.
 -дің бірнеше қасиеттерін жазайық:
-дің бірнеше қасиеттерін жазайық:
- ;
- - сызықты, себебі
 ;
;
- - шенелген, өйткені
 .
.
Лемма 1.
Егер
 болса, онда
болса, онда
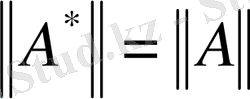 .
.
Дәлелдеуі. 3) -ші қасиеттен, сызықты функционал нормасының анықтамасына сәйкес,
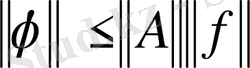 , яғни
, яғни
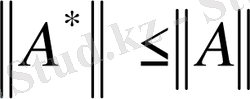 .
.
Әрі қарай, , әрбір
 үшін,
үшін,
 ,
,
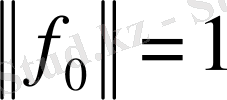 немесе
немесе
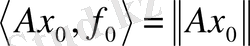 болатын,
болатын,
 фунционалы табылады.
фунционалы табылады.
Бұдан
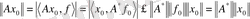
өрнегін аламыз.
Бұдан
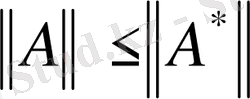 теңсіздігі шығады. Сондықтан
теңсіздігі шығады. Сондықтан
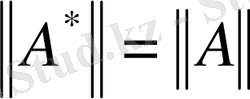 теңдігі орынды болады.
теңдігі орынды болады.
Анықтама 3.
Егер
 болса, яғни оператор өзінің түйіндесімен беттессе, онда
болса, яғни оператор өзінің түйіндесімен беттессе, онда
 операторы өз-өзіне түйіндес деп аталады.
операторы өз-өзіне түйіндес деп аталады.
Анықтамаға сәйкес
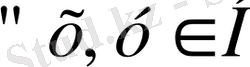 элементтері үшін
элементтері үшін
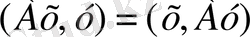
теңдігі орынды болса, онда
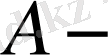 өз-өзіне түйіндес оператор болады.
өз-өзіне түйіндес оператор болады.
Анықтама 4
. Егер
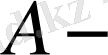 операторы кез келген шенелген жиынды компакт жиынға бейнелесе немес әрбір шенелген
операторы кез келген шенелген жиынды компакт жиынға бейнелесе немес әрбір шенелген
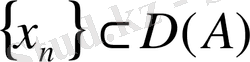 тізбегінің
тізбегінің
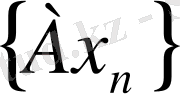 тізбегінде жинақты ішкі тізбегі бар болса онда
тізбегінде жинақты ішкі тізбегі бар болса онда
 операторы жете үзілісіз деп аталады.
операторы жете үзілісіз деп аталады.
Айталық
 жете үзіліссіз оператор болсын. Онда
жете үзіліссіз оператор болсын. Онда
 операторының меншікті мәндері
операторының меншікті мәндері
 операторының
операторының
 сандары деп аталады (Шмидт бойынша меншікті сандары) .
сандары деп аталады (Шмидт бойынша меншікті сандары) .
Еселіктерін ескере отырып нөлдік емес
 сандарын кему ретімен жазамыз
сандарын кему ретімен жазамыз
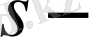 сандарының екінші анықтамасын берейік.
сандарының екінші анықтамасын берейік.
Алдымен Колмогоров бойынша
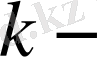 көлденеңдері ұғымының анықтамасы мен олардың қасиеттеріне тоқталайық.
көлденеңдері ұғымының анықтамасы мен олардың қасиеттеріне тоқталайық.
Айталық
 кеңістігіндегі центральді-симметриялы ішкі жиын болсын, яғни
кеңістігіндегі центральді-симметриялы ішкі жиын болсын, яғни
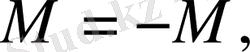
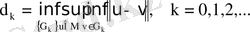
мәні
 жиының к олмогоров бойынша көлденеңдері деп аталады, мұндағы
жиының к олмогоров бойынша көлденеңдері деп аталады, мұндағы
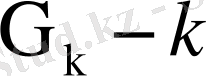 өлшемді ішкі кеңістік.
өлшемді ішкі кеңістік.
Көлденеңдер келесі қасиеттерге ие:
1.
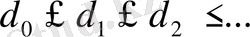
2.
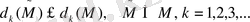
3.
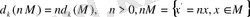
Келесі теорема
 сандарының екінші анықтамасын береді.
сандарының екінші анықтамасын береді.
Теорема 2.
Айталық
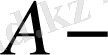 кез келген жете үзіліссіз оператор болсын. Онда
кез келген жете үзіліссіз оператор болсын. Онда
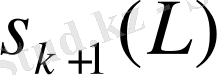 саны
саны
 жиынының
жиынының
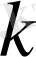 -шы Колмогоров көлденеңімен сәйкес келеді, мұнда
-шы Колмогоров көлденеңімен сәйкес келеді, мұнда
 операторы
операторы
 жиынын
жиынын
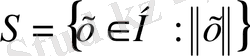 бірлік шарына бейнелейді.
бірлік шарына бейнелейді.
Лемма 2.
Айталық
 шарты орындалсын. Онда
шарты орындалсын. Онда
 болғанда
болғанда
 кеңістігінде анықталаған
кеңістігінде анықталаған
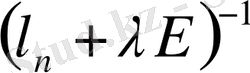 кері оператор табылады, мұндағы
кері оператор табылады, мұндағы
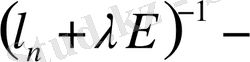
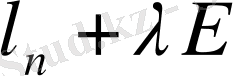 тұйық операторына кері оператор.
тұйық операторына кері оператор.
Лемма 3.
Айталық
 шарты орындалсын. Онда
шарты орындалсын. Онда
 болғанда
болғанда
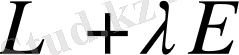 операторы үзіліссіз қайтарымды және ол үшін келесі теңдік орынды:
операторы үзіліссіз қайтарымды және ол үшін келесі теңдік орынды:
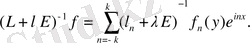
І. Функционалдық анализдің негізгі ұғымдары
1. 1. Сызықты және нормаланған кеңістік
Анықтама 1. 1. 1.
Сызықты кеңістік деп
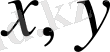 элементтерінің мына төмендегідей шарттарды қанағаттандыратын
элементтерінің мына төмендегідей шарттарды қанағаттандыратын
 жиынын айтады:
жиынын айтады:
І.
 жиынында
жиынында
1) Егер
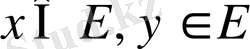 болса, онда
болса, онда
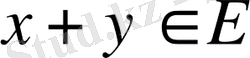 .
.
2)
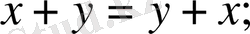
3)
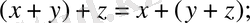
4)
 жиынында барлық
жиынында барлық
 үшін
үшін
 теңдігі орындалатындай «нөлдік» элементтің бар болуы;
теңдігі орындалатындай «нөлдік» элементтің бар болуы;
5) әрбір
 үшін
үшін
 элементі бар,
элементі бар,
 теңдігі дұрыс болатындай (қарама-қарсы элементтің бар болуы) қасиеттерін қанағаттандыратын кез келген
теңдігі дұрыс болатындай (қарама-қарсы элементтің бар болуы) қасиеттерін қанағаттандыратын кез келген
 үшін
үшін
 қосындысы анықталған.
қосындысы анықталған.
ІІ.
 жиынында
жиынында
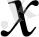 элементтің
элементтің
 санына көбейтіндісі
санына көбейтіндісі
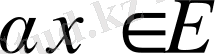 анықталған, сонымен қатар ол мына қасиеттерге ие (мұндағы
анықталған, сонымен қатар ол мына қасиеттерге ие (мұндағы
 скаляр шама) ;
скаляр шама) ;
1.
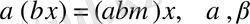 - скалярлар
- скалярлар
2.

3.
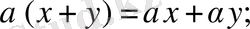
4.
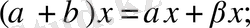
5.
 жиынының элементтерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады. Қандай сандар қорын (барлық нақты сандар немесе комплекс сандар) пайдаланғанға байланысты, комплекс немесе нақты сызықты кеңістіктер деп ажыратамыз.
жиынының элементтерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады. Қандай сандар қорын (барлық нақты сандар немесе комплекс сандар) пайдаланғанға байланысты, комплекс немесе нақты сызықты кеңістіктер деп ажыратамыз.
Егер жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалатыны белгілі. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар анықталған.
Демек, қарапайым амалдар анықталған сандар жиыны немесе векторлар жиыны сызықтық кеңістіктің мысалдары болып табылады.
Сонымен, қайсыбір жиында кез келген екі элементтің қосындысы және элементтің нақты немесе комплекс санға көбейтіндісі анықталса және бұл амалдар жоғарыдағы аксиомаларды қанағаттандарыса, онда бұл жиын сызықтық кеңістікке айналады.
Сызықтық кеңістікке бірқатар мысалдар келтірейік:
1.
 түзу сызығы, яғни қарапайым қосу және көбейту арифметикалық операциялары мен нақты сандар жинағы сызықтық кеңістік болады.
түзу сызығы, яғни қарапайым қосу және көбейту арифметикалық операциялары мен нақты сандар жинағы сызықтық кеңістік болады.
2. Нақты сандар тізбектерінің жиыны
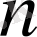 реттелген нақты немесе комплекс сандардың барлық жиыны
реттелген нақты немесе комплекс сандардың барлық жиыны
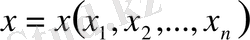 қосу және санға көбейту операциялары мына формалармен анықталса, онда жиын сызықтық кеңістік болады,
қосу және санға көбейту операциялары мына формалармен анықталса, онда жиын сызықтық кеңістік болады,
1)
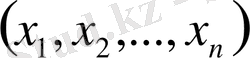 +
+
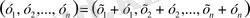
2)
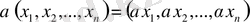
Бұл жиын арифметикалық кеңістік деп аталады және
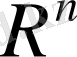 символымен белгіленеді. Осы сияқты комплекс
символымен белгіленеді. Осы сияқты комплекс
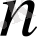 -өлшемді арифметикалық кеңістік
-өлшемді арифметикалық кеңістік
 реттелген
реттелген
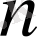 комплекс сандарының жиыны ретінде анықталады( қандай да бір комплекс санға көбейту анықталған болса) .
комплекс сандарының жиыны ретінде анықталады( қандай да бір комплекс санға көбейту анықталған болса) .
3. Функционалдық анализ үшін маңызды болып табылатын
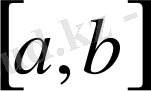 аралығындағы үзіліссіз функциялар
аралығындағы үзіліссіз функциялар
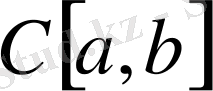 жиыны қарапайым функцияларды қосу және санға көбейту операцияларымен бірге сызықтық кеңістігін құрайды. Үзіліссіз екі функцияның қосындысы да, үзілісіз функцияның санға көбейтіндісі де үзіліссіз функция болғандықтан
жиыны қарапайым функцияларды қосу және санға көбейту операцияларымен бірге сызықтық кеңістігін құрайды. Үзіліссіз екі функцияның қосындысы да, үзілісіз функцияның санға көбейтіндісі де үзіліссіз функция болғандықтан
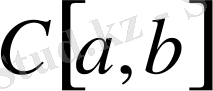 жиынында бұл амалдар анықталған. Қай функцияның да мәні сан болғандықтан, қарастырып отырған мысалда аксиомалардың орындалуы олардың нақты немесе комплекс сандар үшін орындалатындығынан шығады. Нөлдік элемент ретінде бұл кеңістікте
жиынында бұл амалдар анықталған. Қай функцияның да мәні сан болғандықтан, қарастырып отырған мысалда аксиомалардың орындалуы олардың нақты немесе комплекс сандар үшін орындалатындығынан шығады. Нөлдік элемент ретінде бұл кеңістікте
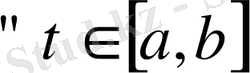 үшін
үшін
 , яғни
, яғни
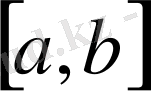 кесіндісінде нөлге тепе-тең функция деп аталады.
кесіндісінде нөлге тепе-тең функция деп аталады.
4.
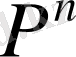 таңбасымен дәрежесі
таңбасымен дәрежесі
 нен аспайтын көпмүшелер
нен аспайтын көпмүшелер
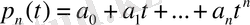 жиынын қарастырайық. Осы жиыннан алынған көпмүшенің қосындысы, санға көбейтіндісі осы жиынға тиісті екендігі белгілі. Сондықтан жиын элементтері сызықтық кеңістік аксиомаларын қанағаттандырады.
жиынын қарастырайық. Осы жиыннан алынған көпмүшенің қосындысы, санға көбейтіндісі осы жиынға тиісті екендігі белгілі. Сондықтан жиын элементтері сызықтық кеңістік аксиомаларын қанағаттандырады.
5.
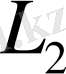 кеңістігі сызықты кеңістік, өйткені оның элементтері
кеңістігі сызықты кеңістік, өйткені оның элементтері
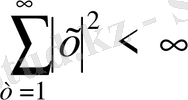
шартын қанағаттандыратын сандар (нақты немесе комплекс) тізбегі
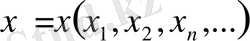
алынады, ол сандар үшін
1)
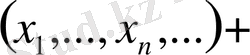
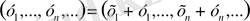
2)
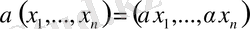 амалдары орындалған.
амалдары орындалған.
Сызықты кеңістікке қатысты кейбір ұғымдар мен анықтамаларды келтірейік.
 сызықты кеңістігіне тиісті
сызықты кеңістігіне тиісті
 элементтерінің әрқайсысын
элементтерінің әрқайсысын
 сандарына көбейтіп нәтижелерін қосу арқылы табылған
сандарына көбейтіп нәтижелерін қосу арқылы табылған
 векторы берілген
векторы берілген
 векторларының сызықты комбинациясы деп аталады.
векторларының сызықты комбинациясы деп аталады.
 сызықтық кеңістігіне тиісті
сызықтық кеңістігіне тиісті
 элементтері үшін олардың сызықтық комбинациясы
элементтері үшін олардың сызықтық комбинациясы
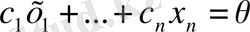 теңдігін тек
теңдігін тек
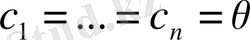 болған жағдайда ғана қанағаттандыратын болса, онда векторлар сызықты тәуелсіз векторлар деп аталады. Егер бұл шарт орындалмайтын болса, яғни
болған жағдайда ғана қанағаттандыратын болса, онда векторлар сызықты тәуелсіз векторлар деп аталады. Егер бұл шарт орындалмайтын болса, яғни
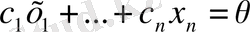 болатындай бәрі бірдей нөлге тең емес коэффициенттер
болатындай бәрі бірдей нөлге тең емес коэффициенттер
 табылса, онда
табылса, онда
 элементтері сызықты тәуелді деп аталады. Егер
элементтері сызықты тәуелді деп аталады. Егер
 элементтері сызықты тәуелді болса, онда бұлардың ең болмағанда бірін басқаларының сызықты комбинациялары түрінде өрнектеуге болады.
элементтері сызықты тәуелді болса, онда бұлардың ең болмағанда бірін басқаларының сызықты комбинациялары түрінде өрнектеуге болады.
Мысал
.
 кеңістігінен
кеңістігінен
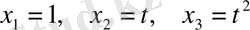 функцияларын қарастырайық. Бұл функциялардың сызықты комбинациясы
функцияларын қарастырайық. Бұл функциялардың сызықты комбинациясы
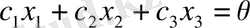 теңдігі
теңдігі
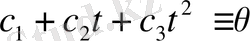 тепе-теңдігімен пара-пар. Квадраттық үшмүше
тепе-теңдігімен пара-пар. Квадраттық үшмүше
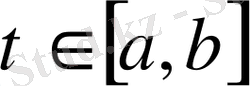 нүктелерінде нөлге айналады, ал кері жағдайда нөлге айналатын нүктелерінің саны екіден аспайтыны белгілі. Сонымен бұл үш функция
нүктелерінде нөлге айналады, ал кері жағдайда нөлге айналатын нүктелерінің саны екіден аспайтыны белгілі. Сонымен бұл үш функция
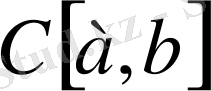 кеңістігіндегі тәуелсіз элементтердің мысалы болады.
кеңістігіндегі тәуелсіз элементтердің мысалы болады.
Егер сызықтық кеңістікте сызықты тәуелсіз
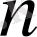 элемент табылса, бірақ осы кеңістікте жатқан кезкелген
элемент табылса, бірақ осы кеңістікте жатқан кезкелген
 элемент сызықты тәуелді болса, онда бұл өлшемі
элемент сызықты тәуелді болса, онда бұл өлшемі
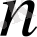 -ге тең кеңістік деп аталады. Егер кез келген натурал сан
-ге тең кеңістік деп аталады. Егер кез келген натурал сан
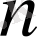 үшін кеңістікте жатқан, сызықты тәуелсіз
үшін кеңістікте жатқан, сызықты тәуелсіз
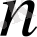 элемент табылатын болса, онда өлшемі ақырсыз кеңістік деп аталады.
элемент табылатын болса, онда өлшемі ақырсыз кеңістік деп аталады.
 ішкі жиыны өз бетінше сызықты кеңістік құрайтын болса, онда
ішкі жиыны өз бетінше сызықты кеңістік құрайтын болса, онда
 ішкі жиыны
ішкі жиыны
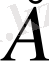 кеңістігінің ішкі кеңістігі деп аталады. Анығырақ айтқанда,
кеңістігінің ішкі кеңістігі деп аталады. Анығырақ айтқанда,
 ішкі жиынындағы элементтерге
ішкі жиынындағы элементтерге
 кеңістігінде анықталған амалдар қолдану нәтижесінде пайда болған элементтер
кеңістігінде анықталған амалдар қолдану нәтижесінде пайда болған элементтер
 жиынында болу керек.
жиынында болу керек.
Сызықтық кеңістікте ішкі кеңсітік ұғымына тығыз байланысты тағы бір ұғымды анықтайық. Егер кез келген
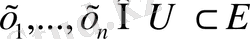 векторлары мен бірге олардың кез-келген сызықты комбинациясы да осы
векторлары мен бірге олардың кез-келген сызықты комбинациясы да осы
 жиынында жататын болса, онда
жиынында жататын болса, онда
 жиыны сызықты көпбейнелік деп аталады.
жиыны сызықты көпбейнелік деп аталады.
Анықтама 1. 1. 2.
 және
және
 сызықтық кеңістіктер изоморфты деп аталады, егер олардың элементтерінің арасында өзара бір мәнді сәйкестік орнатуға болса және ол сәйкестік
сызықтық кеңістіктер изоморфты деп аталады, егер олардың элементтерінің арасында өзара бір мәнді сәйкестік орнатуға болса және ол сәйкестік
 және
және
 кеңістіктеріндегі операцияларымен былай байланыссын:
кеңістіктеріндегі операцияларымен былай байланыссын:
Егер
 ,
,
 болса, мұндағы
болса, мұндағы
 ,
,
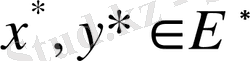 ,
,
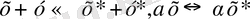
Анықтама 1. 1. 3.
Егер барлық
 үшін нақты сан мәнді
үшін нақты сан мәнді
 функциясы анықталса және ол мына шарттарды қанағаттандыратын болса :
функциясы анықталса және ол мына шарттарды қанағаттандыратын болса :
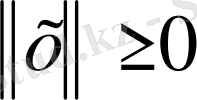
1)
 және тек
және тек
 болғанда ғана
болғанда ғана
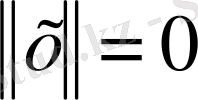 (норманың теріс еместік шарты) ;
(норманың теріс еместік шарты) ;
2) кез келген
 саны үшін
саны үшін
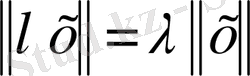 (норманың біртектілік шарты) ;
(норманың біртектілік шарты) ;
3) кез келген
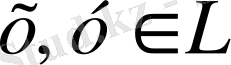 үшін
үшін
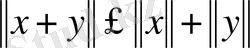 (үшбұрыш теңсіздігі),
(үшбұрыш теңсіздігі),
онда кеңістігінде норма анықталған дейміз.
Анықтамада келтірілген 1), 2), 3) шарттары норманың аксиомалары деп аталады.
Норма анықталған сызықты кеңістік нормаланған сызықты кеңістік деп аталады.
Берілген
 сызықтық кеңістігінде норманы әртүрлі анықтауға болады. Осыған байланысты бір жиынның негізінде әртүрлі нормаланған сызықтық кеңістіктер пайда болатыны төмендегі мысалдардан байқалады.
сызықтық кеңістігінде норманы әртүрлі анықтауға болады. Осыған байланысты бір жиынның негізінде әртүрлі нормаланған сызықтық кеңістіктер пайда болатыны төмендегі мысалдардан байқалады.
Мысалдар:
1.
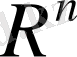 -сызықтық кеңсітігін нормаланған сызықты кеңістікке айналдырамыз. Кеңістікке тиісті әрбір элемент
-сызықтық кеңсітігін нормаланған сызықты кеңістікке айналдырамыз. Кеңістікке тиісті әрбір элемент
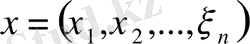 үшін норманы
үшін норманы
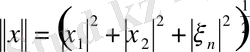 (1. 1. 1. )
(1. 1. 1. )
теңдігімен анықтаймыз. Осылай анықталған норма норманың аксиомаларын қанағаттандыратынын тексеру қажет. Бірінші шарттың орындалатындығы (1. 1. 1) теңдігінің оң жағындағы өрнектің теріс емес екендігінен көруге болады.
Егер
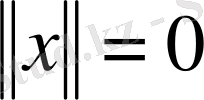 болса, онда барлық
болса, онда барлық
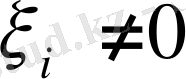 . Себебі, егер қайсыбір
. Себебі, егер қайсыбір
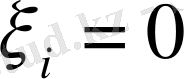 болса, онда (1. 1. 1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын. Сонымен, егер
болса, онда (1. 1. 1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын. Сонымен, егер
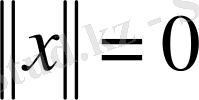 болса, онда векторының барлық координаттары нөлге тең:
болса, онда векторының барлық координаттары нөлге тең:
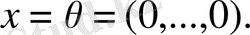 Керісінше, егер
Керісінше, егер
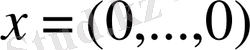 болса, онда
болса, онда
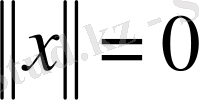 екені айқын.
екені айқын.
Екінші аксиома оңай тексеріледі:
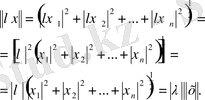 (1. 1. 2)
(1. 1. 2)
Үшінші аксиома, яғни үшбұрыш теңсіздігі орындалатынын дәлеледеу үшін алдымен Коши теңсіздігін еске алайық. Кез келген
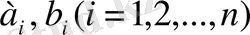 нақты сандары үшін
нақты сандары үшін
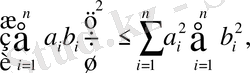 (1. 1. 3)
(1. 1. 3)
теңсіздігі орындалады. Бұл теңсіздіктің екі жағынан квадрат түбір алып, оны мына түрде жазуға болады:
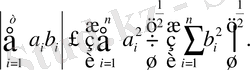 (1. 1. 4)
(1. 1. 4)
Енді осы теңсіздікті пайдаланып (1. 1. 1) нормасы үшін үшбұрыш теңсіздігін дәлелдейік:
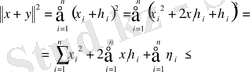
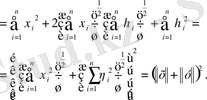
Теңсіздіктің екі жағынан квадрат түбір алып, үшбұрыш теңсіздігіне келеміз.
Сонымен (1. 1. 1) теңдігімен анықталған норма аксиомаларын қанағаттандыратыны айқын болды.
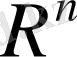 жиыны нормаланған сызықты кеңсітікке айналды. Бұл кеңістік, негізінен, арифметикалық Евклид кеңістігі деп, ал норма (1. 1. 1) - Евклид нормасы деп аталады.
жиыны нормаланған сызықты кеңсітікке айналды. Бұл кеңістік, негізінен, арифметикалық Евклид кеңістігі деп, ал норма (1. 1. 1) - Евклид нормасы деп аталады.
2.
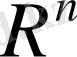 сызықты кеңістігінде норманы басқаша, атап айтқанда,
сызықты кеңістігінде норманы басқаша, атап айтқанда,
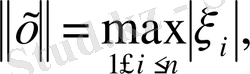 (1. 1. 5)
(1. 1. 5)
Теңдігі арқылы енгізіліп, сол жиында анықталған тағы бір нормаланған сызықты кеңістікті аламыз. . Норманың аксиомалары орындалатынын тексеру бұл жолы оңай. Расында, (1. 1. 5) өрнегінен норманың теріс болмайтындығын көруге болады және
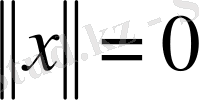 болуы барлық
болуы барлық
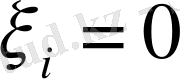 болғанда, тек қана осы жағдайда болады, яғни
болғанда, тек қана осы жағдайда болады, яғни
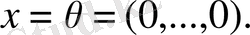
Сондай-ақ, екінші, үшінші аксиомалардың тексерілуі де қиын емес:
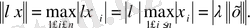 (1. 1. 7)
(1. 1. 7)
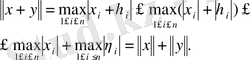 Егер
Егер
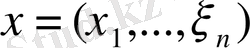 және
және
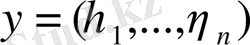 кеңістіктің кез келген екі векторы болса, онда
кеңістіктің кез келген екі векторы болса, онда
яғни үшбұрыш теңсіздігі орындалады.
3.
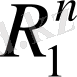 символымен
символымен
 сызықты кеңістігінде норманы
сызықты кеңістігінде норманы
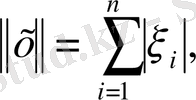 (1. 1. 8)
(1. 1. 8)
теңдігімен анықтау нәтижесінде пайда болған нормаланған сызықты кеңістікті белгілейміз.
4.
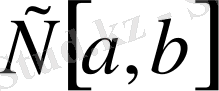 сызықты кеңістігіндегі
сызықты кеңістігіндегі
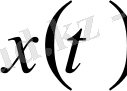 функциясының нормасы
функциясының нормасы
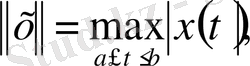 (1. 1. 9)
(1. 1. 9)
теңдігімен анықталады.
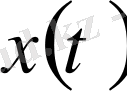 функциясы
функциясы
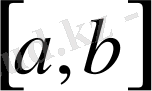 кесіндісінде үзіліссіз болғандықтан, оның модулі де үзілісіз, демек, осы кесіндіде максимумы бар. Сондықтан (1. 1. 9) теңдігі
кесіндісінде үзіліссіз болғандықтан, оның модулі де үзілісіз, демек, осы кесіндіде максимумы бар. Сондықтан (1. 1. 9) теңдігі
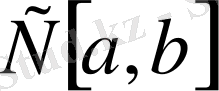 жиынынң әрбір элементі
жиынынң әрбір элементі
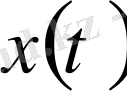 үшін оның нормасының мәнін бір мәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
үшін оның нормасының мәнін бір мәнді анықтайды. Модулінің максимумы нөлге тең функция тек қана
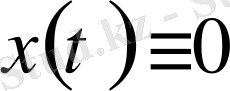 екендігі түсінікті. Сонымен бірінші аксиоманың орныдалуы айқын. Енді
екендігі түсінікті. Сонымен бірінші аксиоманың орныдалуы айқын. Енді
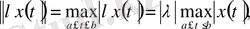
теңдігі мен
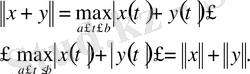
теңсіздігі норманың қалған екі аксиомасы да орындалатынын көрсетеді.
- Гильберт кеңістігі, кеңістігі
Анықтама 1. 2. 1.
Егер
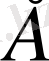 сызықты кеңістігінде кез келген
сызықты кеңістігінде кез келген
 үшін екі айнымалылы, сан мәнді функция
үшін екі айнымалылы, сан мәнді функция
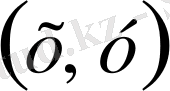 анықталған және ол төмендегі шарттарды қанағаттандыратын болса:
анықталған және ол төмендегі шарттарды қанағаттандыратын болса:
- (симметриялық қасиеті) ;
- (аддитивтік қасиеті) ;
- (біртектілік қасиеті) ;
4)
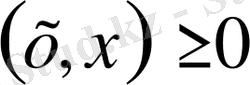 және
және
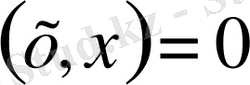 тек қана
тек қана
 болғанда ғана мүмкін, онда
болғанда ғана мүмкін, онда
 кеңістігінде скаляр көбейтінді анықталған дейміз. 1) -4) шарттары скаляр көбейтіндінің аксиомалары деп аталады.
кеңістігінде скаляр көбейтінді анықталған дейміз. 1) -4) шарттары скаляр көбейтіндінің аксиомалары деп аталады.
Анықтама 1. 2. 2.
Скаляр көбейтінді анықталған сызықтық кеңістік гильберт кеңістігі деп аталады. Гильберт кеңістігін
 арқылы белгілейміз.
арқылы белгілейміз.
Егер анықтама бойынша скаляр көбейтіндінің мәндері нақты сандар болса
және векторлар нақты сандарға көбейтілетін болса, онда анықталған гильберт кеңістігі нақты кеңістік деп аталады. Комплекс кеңістік жағдайында симметриялық жағдайы
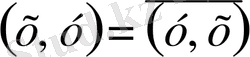 түрінде жазылады., яғни элементердің орындары ауысқанда скаляр көбейтіндінің мәні түйіндес комплекс санға өзгереді.
түрінде жазылады., яғни элементердің орындары ауысқанда скаляр көбейтіндінің мәні түйіндес комплекс санға өзгереді.
2) -3) аксиомалар бірінші аргументтке қатысты болса да, симметриялық аксиоманың салдарынан олар екінші аргумент үшін де орындалады. Расында,
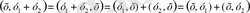
Осыған ұқсас, 3) -аксиомадағы
 санын екінші аргументтің қасынан көбейтіндінің алдына шығаруға болатынын, яғни
санын екінші аргументтің қасынан көбейтіндінің алдына шығаруға болатынын, яғни
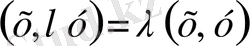 екнін байқаймыз. Бұл теңдік комплекс кеңістік жағдайында
екнін байқаймыз. Бұл теңдік комплекс кеңістік жағдайында
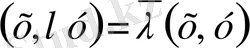 түрінде болады. Расында,
түрінде болады. Расында,
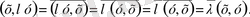
Гильберт кеңістігінде
 элементінің нормасын
элементінің нормасын
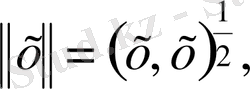 (1. 2. 1)
(1. 2. 1)
теңдігімен анықтауға болады. м Норма аксиомалары орындалатыны скаляр көбейтіндінің аксиомаларының салдары ретінде шығады.
Расында, норманың бірінші аксиомасы скаляр көбейтіндінің төртінші аксиомасынан тікелей шығатыны айқын. Норманың екінші аксиомасы орындалатыны да скаляр көбейтіндінің үшінші қасиетінен тікелей шығады:
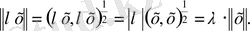
Енді (1. 2. 1) теңдігімен анықталған норма үшбұрыш теңсіздігін қанағаттандыратынын дәлелдейік. Сол үшін
 элементтері және кез келген
элементтері және кез келген
 саны үшін
саны үшін
 элементінің скаляр квадратын қарастырайық:
элементінің скаляр квадратын қарастырайық:
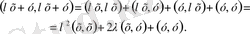
Скаляр көбейтіндінің 4) - аксиомасы боынша элементтің скаляр квадраты теріс емес сан, демек,
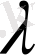 санының мәні қандай болса да
санының мәні қандай болса да
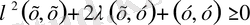 .
.
Басқаша айтқанда, квадрат үшмүшенің дискриминанты оң сан емес:
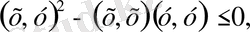 яғни
яғни
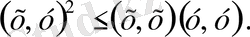
Осы теңсіздіктің екі жағынан квадрат түбір алып, мына түрде
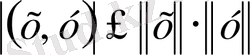 .
.
Соңғы теңсіздіктен скаляр көбейтіндінің абсолют шамасы көбейтілген векторлардың нормаларының көбейтіндісінен аспайтынын көреміз.
 Лебег кеңістігі.
Лебег кеңістігі.
 жиынында қосындыланатын функциялардың жиыны сызықты кеңістік құрайды. Бұл кеңістік
жиынында қосындыланатын функциялардың жиыны сызықты кеңістік құрайды. Бұл кеңістік
 түрінде таңбаланады. Енді
түрінде таңбаланады. Енді
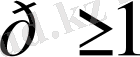 кез келген нақты сан болсын.
кез келген нақты сан болсын.
 жиынында
жиынында
 дәрежесі қосындыланатын
дәрежесі қосындыланатын
 функцияларының жиыны да сызықты кеңістік құрайтыны белгілі. Осы сызықты кеңістік
функцияларының жиыны да сызықты кеңістік құрайтыны белгілі. Осы сызықты кеңістік
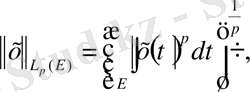 (1. 2. 2)
(1. 2. 2)
теңдігімен анықталған норма енгізу арқылы нормаланған сызықты кеңістікке айналады. Бұл кеңістік әдетте
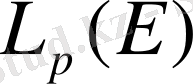 түрінде белгіленеді. Сонымен, әрбір
түрінде белгіленеді. Сонымен, әрбір
санына сәйкес сызықты кеңістік
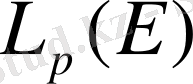 анықталды. Осы кеңістіктер Лебег кеңістіктері деп аталады. Егер
анықталды. Осы кеңістіктер Лебег кеңістіктері деп аталады. Егер
 болса, онда
болса, онда
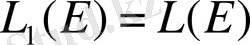 түрінде жазылып, қосындыланатын функциялар кеңістігін белгілейді.
түрінде жазылып, қосындыланатын функциялар кеңістігін белгілейді.
(1. 2. 2) теңдігі арқылы анықталған норманың тиісті аксиомалары қанағаттандыратынына тоқталайық. Онда теріс емес сан екендігі айқын. Егер қайсыбір
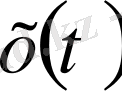 үшін
үшін
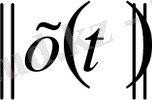 нормасының нөлге тең болуы, теңдіктің оң жағындағы интеграл нөлге тең емес екендігін көрсетеді. Демек, Лебег интегралының қасиеті бойынша
нормасының нөлге тең болуы, теңдіктің оң жағындағы интеграл нөлге тең емес екендігін көрсетеді. Демек, Лебег интегралының қасиеті бойынша
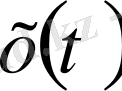 функциясы нөлге пара-пар функция. Осыған байланысты Лебег кеңістіктерінде қабылданған маңызды келісім - бұл кеңістікте пара-пар функциялар ажыратылмайды, өзара пара-пар функциялардың барлығы кеңістіктің бір элементі болып есептеледі.
функциясы нөлге пара-пар функция. Осыған байланысты Лебег кеңістіктерінде қабылданған маңызды келісім - бұл кеңістікте пара-пар функциялар ажыратылмайды, өзара пара-пар функциялардың барлығы кеңістіктің бір элементі болып есептеледі.
 кеңістігінде нөлге пара-пар, яғни осы жиынның барлық жерінде дерлік нөлге тең функция кеңістіктің нөлдік элементі ретінде қабылданады. Сондықтан (1. 2. 2) теңдігімен анықталған норма норманың бірінші аксиомасын қанағаттандырады. Екінші аксиоманың орындалуы біртектілік қасиеттен шығады. Ендігі кезекте норма (1. 2. 2) үшбұрыш теңсіздігін атап айтқанда,
кеңістігінде нөлге пара-пар, яғни осы жиынның барлық жерінде дерлік нөлге тең функция кеңістіктің нөлдік элементі ретінде қабылданады. Сондықтан (1. 2. 2) теңдігімен анықталған норма норманың бірінші аксиомасын қанағаттандырады. Екінші аксиоманың орындалуы біртектілік қасиеттен шығады. Ендігі кезекте норма (1. 2. 2) үшбұрыш теңсіздігін атап айтқанда,
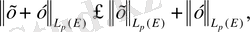 (1. 2. 3)
(1. 2. 3)
теңсіздігін дәлелдеу.
Алдымен Гелдер теңсіздігін еске алайық (
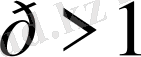 ) .
) .
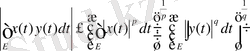 . (1. 2. 4)
. (1. 2. 4)
Мұнда
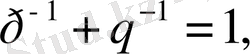 немесе осыдан,
немесе осыдан,
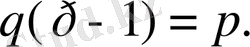 Енді (1. 2. 3) теңсіздігін дәлелдейік. Келесі түрлендіруде
Енді (1. 2. 3) теңсіздігін дәлелдейік. Келесі түрлендіруде
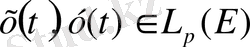 , сондай-ақ
, сондай-ақ
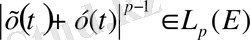 екендігі пайдаланылды. Ықшамдық үшін норманың қасындағы
екендігі пайдаланылды. Ықшамдық үшін норманың қасындағы
 белгісін жазбаймыз.
белгісін жазбаймыз.

Мұнда бірінші теңдік - анықтама бойынша. Екінші теңдіктен кейін қосындының бір дәрежесі жеке жазылды да, келесі теңсіздіктен кейін екі қосындыға жіктеліп, олардың әрқайсысына гельдер теңсіздігі қолданылды. Соңында ортақ көбейткіш тік жақша сыртына шығарылды. Алынған теңсізідік норманың анықтамасы бойнынша мына түрде жазылады:
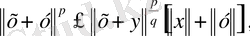
осы теңсіздіктің екі жағын
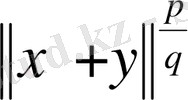 санына бөліп, (1. 2. 3) теңдігіне келеміз. Сонымен теңдік (1. 2. 2) норма анықтайтыны дәлелденді, демек,
санына бөліп, (1. 2. 3) теңдігіне келеміз. Сонымен теңдік (1. 2. 2) норма анықтайтыны дәлелденді, демек,
 нормаланған сызықты кеңістік болады.
нормаланған сызықты кеңістік болады.
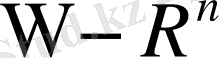 кеңістігіндегі ашық облыс,
кеңістігіндегі ашық облыс,
 арқылы
арқылы
 жиынының тұйықталуын белгілейміз.
жиынының тұйықталуын белгілейміз.
Анықтама 1. 2. 3.
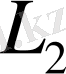 кеңістігі деп
кеңістігі деп
 жиынында лебег бойынша өлшемді функциялардан құралған гильберт кеңістігін айтады. Бұл кеңістікте норма келесі түрде анықталады:
жиынында лебег бойынша өлшемді функциялардан құралған гильберт кеңістігін айтады. Бұл кеңістікте норма келесі түрде анықталады:
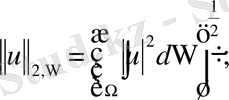
1. 3. Сызықты операторлар теориясының элемменттері
Анықтама 1. 3. 1.
 кез келген сызықты кеңістік болсын. Осы кеңістіктің элементтерінде анықталған сан мәнді
кез келген сызықты кеңістік болсын. Осы кеңістіктің элементтерінде анықталған сан мәнді
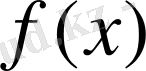 функциясы функционал деп аталады. Мұнда, әдеттегідей,
функциясы функционал деп аталады. Мұнда, әдеттегідей,
 сәйкестікті анықтайтын ережені, ал
сәйкестікті анықтайтын ережені, ал
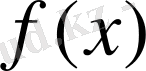 таңбасы
таңбасы
 элементіне сәйкес қойылған санды белгілейді. Кеңістігінің құрылымына қарай
элементіне сәйкес қойылған санды белгілейді. Кеңістігінің құрылымына қарай
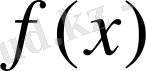 нақты не комплекс мәнді функционал болуы мүмкін. Мысалы,
нақты не комплекс мәнді функционал болуы мүмкін. Мысалы,
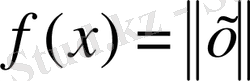 әрқашан нақты мәнді функционал.
әрқашан нақты мәнді функционал.
Егер
 функционалы үшін мына екі шарт орындалатын болса:
функционалы үшін мына екі шарт орындалатын болса:
1. кез келген
 үшін
үшін
 (аддитивтік шарты)
(аддитивтік шарты)
2. кез келген
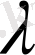 саны үшін
саны үшін
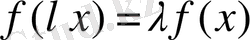 (біртектілік шарты)
(біртектілік шарты)
онда
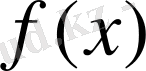 сызықтық функционал деп аталады. Бұл екі шартты біріктіріп, мына бір теңдік түрінде қолдануға да болады:
сызықтық функционал деп аталады. Бұл екі шартты біріктіріп, мына бір теңдік түрінде қолдануға да болады:
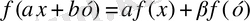 ,
,
мұнда
 және
және
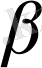 кез келген сандар. Бұл теңдік анықтамадағы екі шартқа пара-пар болғандықтан, функционалдың сызықтылығын тексеру үшін теңдігін тексеру жеткілікті.
кез келген сандар. Бұл теңдік анықтамадағы екі шартқа пара-пар болғандықтан, функционалдың сызықтылығын тексеру үшін теңдігін тексеру жеткілікті.
Сызықты функционалдарға мысалдар келтірейік.
1.
 кеңістігінің
кеңістігінің
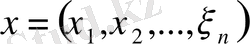 элементінде
элементінде
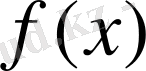 функционалының мәні
функционалының мәні
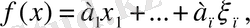
теңдігімен анықталған, мұнда
 тұрақты сандар. Бұл функционалдың аддитивтік және біртектілік қасиеттерін тексеру оңай.
тұрақты сандар. Бұл функционалдың аддитивтік және біртектілік қасиеттерін тексеру оңай.
 кеңістігінде анықталған бұл функционалдың сызықты функция екендігіне зер салайық. Кейін
кеңістігінде анықталған бұл функционалдың сызықты функция екендігіне зер салайық. Кейін
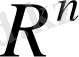 кеңістігіндегі сызықтық функционал тек осы түрде болатын айқындалады.
кеңістігіндегі сызықтық функционал тек осы түрде болатын айқындалады.
2.
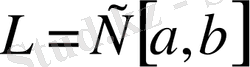 сызықты кеңістігінде
сызықты кеңістігінде
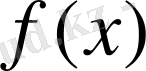 функционалының
функционалының
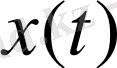 элементіндегі
элементіндегі
мәні
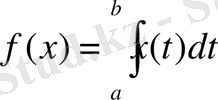
теңдігімен анықталған. Бұл функционалдың сызықты қасиеті интегралдың аддитивтік және біртектілік қасиеттерінен тікелей шығады.
3.
 қосындыланатын функциялар кеңістігінде
қосындыланатын функциялар кеңістігінде
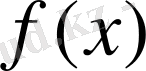 функционалының
функционалының
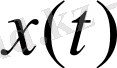 элементіндегі мәні қайсыбір шенелген, тиянақты
элементіндегі мәні қайсыбір шенелген, тиянақты
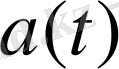 функциясы арқылы
функциясы арқылы
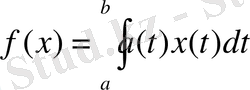
теңдігімен анықталған. Бұл функционалдың да сызықтық қасиеті интегралдың қасиеттерінен шығады және бұл
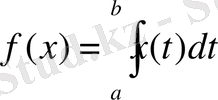 функционалының жалпыланған түрі .
функционалының жалпыланған түрі .
4.
 кеңістігінде анықталған тағы бір функционал
кеңістігінде анықталған тағы бір функционал
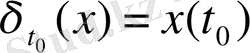 ,
,
яғни
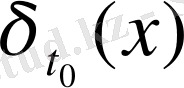 функционалының
функционалының
 элементіндегі мәні
элементіндегі мәні
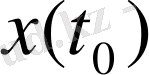 санына тең. Анықтаушы теңдік бойынша
санына тең. Анықтаушы теңдік бойынша
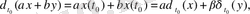
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz