Беттің майысуы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

II тарау

§5. Беттің майысуы

1. Изометриялық беттер. Ұзындықтары сәйкес келетін қисық және беттерде тең болса және осы беттің нүктелерінің арасында бір мәнді сәйкестік орнатылса, онда және беттері изометриялық деп аталады. Егер екі бет изометриялық болса, онда оның әрқайсысы екіншісіне майысуы болып табылады. Басқаша айтқанда, беттің майысуы - беттегі қисықтың ұзындығы өзгермейтін деформация.

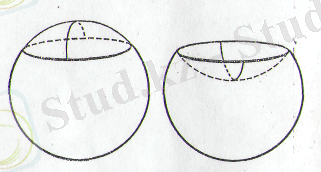
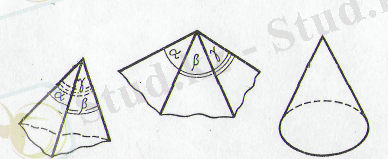
Жазықтықтың екіжақты бұрышқа немесе параболалық цилиндрге майысуын көз алдыңа елестету оңай (1-сурет) . Көпжақты дөңес бұрыштың майысуы мысалы, берілген көпжақты бұрыш сияқты жазылуы және жазық бұрыштары бар үшжақты конустық бетке үштік мысал болып табылады (2-сурет) .

Мысал келтірейік, егер 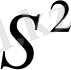сферасынан жазық сфералық сегмент кесіп алатын болсақ, онда қабырғасы бар және 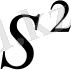сферасына изометриялы болатын ойыс 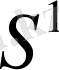бетін аламыз (3-сурет) .

- жатық беттер үшін келесі жеткілікті изометрия белгісі дұрыс.

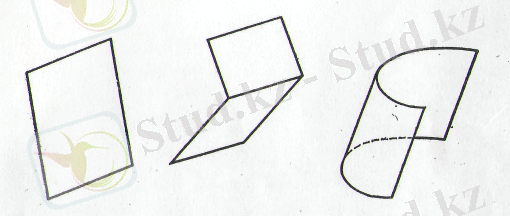
1- сурет

3- сурет

2- сурет

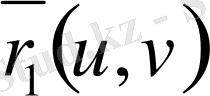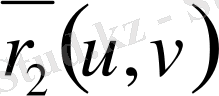Теорема1 және беттері - класының және вектор функциясы түрінде берілген болса, онда . Егер және беттерінің бірінші квадраттық формасының коэффициенттері D облысына тең болса, онда барлық 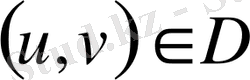болады.

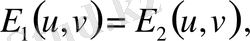
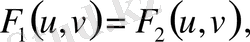
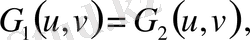(1) болса, онда және изометриялық.

Дәлелдеу: және беттің нүктелерінің арасындағы келесі сәйкестікті орнатамыз: және нүктелері 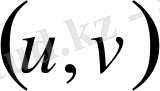координаталарымен сәйкес келеді деп есептейік. Егер - жатық қисық, ал -ге мына теңдеу түрінде берілсе

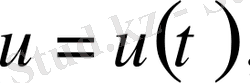
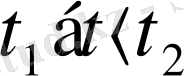
Онда оған сәйкесінше қисық дәл сол теңдеу түрінде беріледі. Ондай жағдайда (1) теңдеуді қолданамыз

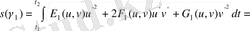
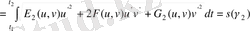
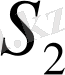бұдан және беттерінің изометрияля екендігі шығады.

Теорема дәлелденді.

(1) шарт изометриялық екі беттің қажетті шарттары және белгілі мәндері болып табылады. Ал негізі келесі теорема дұрысырақ.

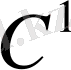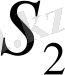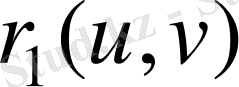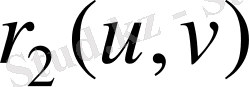Теорема2. -жатық беттер және -ге изометриялы болсын, -ның кез келген облысында берілген болса, және вектор-функцияларының параметрленуіне жол береді. Онда, егер изометрия бойынша сәйкес нүктелер ішкі координаталары 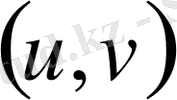бірдей болса, теңдік орны (1) болады.

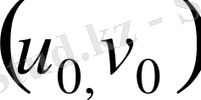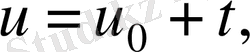
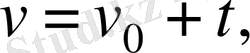
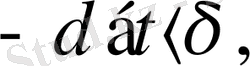
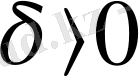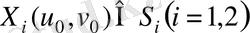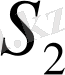Дәлелдеу: - D облысының туынды нуктесі болсын. бетіндегі u сызықтарын қарастыратын болсақ, ол сызықтар ішкі теңдеумен берілген , жазықтығы қисық D облысында жатқан осы теңдеумен берілген ең кіші мәнін аламыз. нүктелеріне параметрі жауапты. және беттерінің ұзындықтарымен тең болады.

Сондықтан

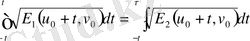(2)

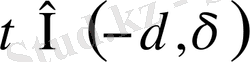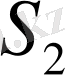теңдігі кез келген үшін дұрыс. және беттері 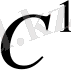класына кіргендіктен, бірінші квадраттық форманың 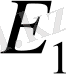және коэффициенттері үздіксіз болады. Орта туралы теореманы қолдана отырып, (2) теңдіктен мынаны аламыз

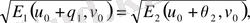
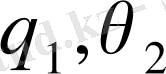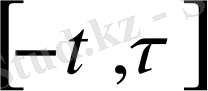- аралығында жататын t параметрінің кейбір мәндері болып табылады. 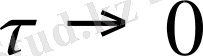ұмтылғанда, мынадай теңдік аламыз

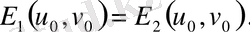(3)

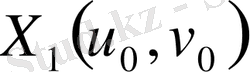және 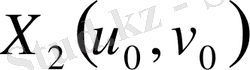нүктелері арқылы өтетін, және 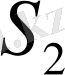беттеріндегі v сызықтарын қарастырсақ, мынадай теңдік аламыз

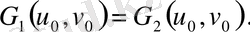(4)

Сонымен, егер төмендегі ішкі теңдеумен берілген және беттеріндегі қисықтың доғаларын қарастырсақ

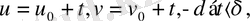
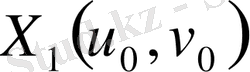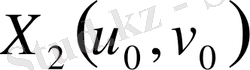сірә, сәйкесінше және нүктелері арқылы өтетін және және изометриясымен қолдансақ, онда мынадай теңдік аламыз

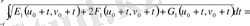
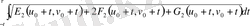
кез келген мәндері үшін орынды. Орта туралы теореманы қолдана және 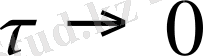ұмтылдыра отырып, мынадай теңдік аламыз:

Бұл теңдіктен және (3), (4) теңдіктерден мынаны аламыз

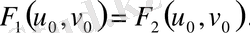(5) Теорема дәлелденді.

2. Беттің ішкі геометриясы жайында түсінік. Екі бетті алып қараса, алынған майысумен олардың көптеген қасиеттерінің бірдей, ал формалры әр түрлі болатынын көрсетеді. Сондықтан майысуда өзгермейтін беттер теориясының осындай түсініктері мен фактілерін үйрену мақсатқа сай келеді. Бұл түсініктер мен фактілер беттің ішкі геометриясының мазмұнын құрайды.

Егер беттер 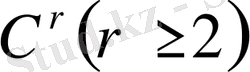класында жататын болса, жатық беттің ішкі геометриясы тек бірінші квадраттық формаы ғана анықтайтын түсініктер мен фактілердіүйретеді. Беттегі қисық ұзындықтары, қисықтар арасындағы бұрыштар, облыстардың аудандары ішкі геометрияға қатысты. Гаусс теңдеуінен гаустық беттің иілімі ішкі геометрия объектісі болып табылады және беттің майысуларында өзгермейді деген тұжырым шығады. Бұл фактінің Гаусқа әсер еткені сондай, ол оны «жарқыраған теорема» деп атады. Гаустың теоремасынан беттегі нүктелердің типі майысуларда өзгермейді, яғни ішкі беттеріне тиісті. Сондықтан майысумен элиптикалық нүктені параболалық немесе гиперболалыққа аударуға болмайды.

Беттердің ішкі геометриясы түсінігін Гаусс енгізген.

§6. Беттегі қисықтың геодезиялық иілімі.

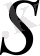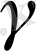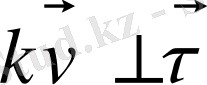
1. Геодезиялық иілімдерді анықтау . бетіндегі класының -жатық қисық түрінде берілген деп есептейік. 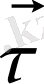- Х нүктесіндегі 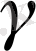-ға жанама бірлік вектор, ал 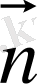- Х нүктесіндегі 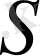бетіне нормаль, 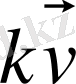- 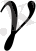қисығының нүктесіндегі иілім векторы, 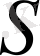- 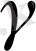қисығының натурал параметрі.

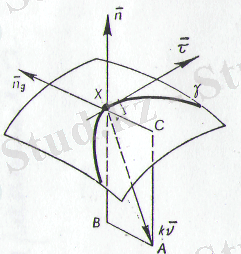
Х нүктесіндегі ортонормаланған базисін қарастырайық

(1-сурет) . Онда

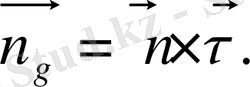
Х нүктесіндегі қисығының иілім векторын 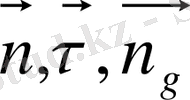базисі бойынша жіктейміз. болғандықтан, бұл жіктеу мынадай түрде болады:

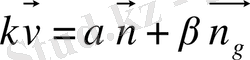, (1)

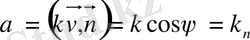одан, (2)

және

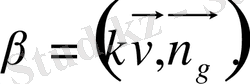(3) екені белгілі.

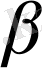ені нүктесіндегі

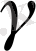
қисығының геодезиялық иілімі деп

аталады және -мен белгіленеді.

Осылайша

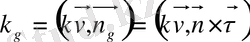
Френенің бірінші формуласынан

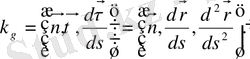(4) 1 - сурет

теңдеу аламыз.

Бұдан, иілім векторы

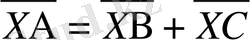онда 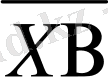нормаль иілімінің векторы деп аталады, ал 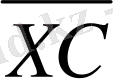-геодезиялық иілімнің векторы деп аталады. Х нүктесіндегі қисығының нормалі және геодезиялық иілімнің модулі осы вектордың ұзындығымен сәйкес болады.

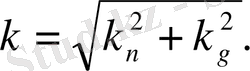(5)

Геодезиялық иілімнің геометриялық мағынасын қарастырсақ, келесі теоремаға келеміз.

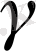Теорема1. класының бетінде класының қисығы жатсын және қисығының Х-кейбір нүктесі болсын. 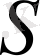бетіндегі Х нүктесінде 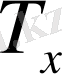жанасушы жазықтыққа 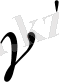-ортогональдық проекция болсын. Онда Х нүктесіндегі қисығының геодезиялық иілімінің абсолюттік еніне тең болады.

Дәлелдеу: Бұл теоремада локальді факт жайында әңгіме болғандықтан, қарастыруды бетіндегі Х нүктесінің шексіз аз аймағына кіргізуге болады, бұл дегеніміз - 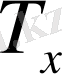жазықтығында -жатық қисық болып табылады. арқылы параллельдік нормалін орнататын цилиндрлік бет жүргіземіз (2-сурет) .

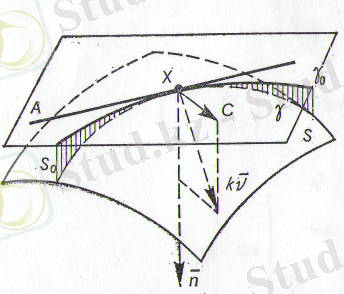
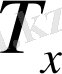жанама жазықтығымен қиылысатын

бұл цилиндрлік бет класының

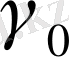қисығын береді, бұл дегеніміз

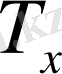жазықтығына 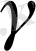қисығы ортогональді

проекция болып табылады. Бұдан,

жанама жазықтық -ге Х нүктесінде

параллельдік вектор орнататын және 2- сурет

жанама қисығы арқылы өтеді, онда нормаль 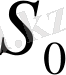жанама жазықтығына 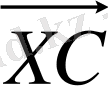векторының Х нүктесіндегі 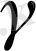қисығының геодезиялық иілімі бағытында жүреді. Әрине, Х нүктесіндегі 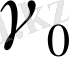-ге жанама 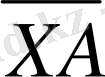-мен тура сәйкес келеді, дәл сол сияқты 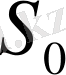цилиндрлік бетінде жатқан 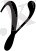және 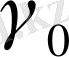жалпы жанама болып табылады. Мұндай жағдайда 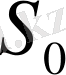бетіндегі 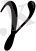және 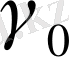қисықтарының нормаль иілімдері сәйкес келеді. 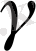-ны цилиндрлік бетіне қисық деп қарастыратын болсақ, онда оның Х нүктесіндегі нормаль иілім векторы векторы болып табылады. бетіндегі қисығына қолданылған Менье теоремасы бойынша, оның Х нүктесіндегі иілімі 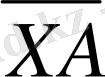бағытындағы Х нүктесінде 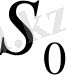бетіндегі нормаль иілімнің абсолиттік еніне тең болады. 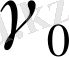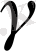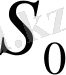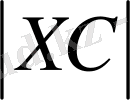Бұдан шығатыны Х нүктесіндегі қисығының иілімі Х нүктесіндегі қисығының нормаль иілімінің модуліне тең болады, бетіндегі қисық ретінде қарастыратын болсақ, -ке қисық ретінде қарастырылған Х нүктесіндегі 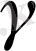қисығының геодезиялық иілімінің модуліне тең.

Теорема дәлелденді.

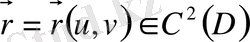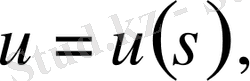
2. Геодезиялық иілім-ішкі геометрияның объектісі. - ж атық бетіне класының қисығы мына параметрлер арқылы берілген болсын. Ал мынадай ішкі теңдеулер арқылы берілген болсын, мұнда -ға натурал параметр. қисығының геодезиялық иілімін есептеу үшін формула табамыз. Ол үшін (4) формуласын қолданамыз.

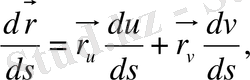
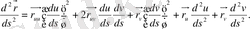
Деривациондық формулалармен қолдана отырып, мынадай теңдеу аламыз:

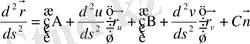
онда

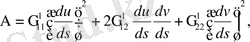
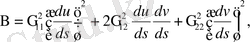
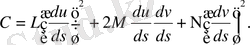
бұдан алатынымыз

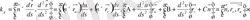
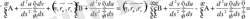
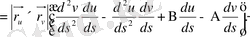
Нәтижесінде мынадай теңдеу аламыз:

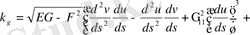
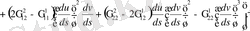(6)

Осы (6) теңдеуден келесі маңызды теорема шығады.

Теорема2. Геодезиялық иілім беттің ішкі геометриясының объектісі болып табылады.

Осылайша, беттің иілуінде кез келген қисықтың геодезиялық иілімі оған өзгермейді. (5) формуладан шығатыны беттегі қисықтың иілімі оның иілуінде, нормаль иілімінің өзгеруінде ғана ауысады, яғни беттің формасының өзгеруіне байланысты.

§7. Беттегі геодезиялық сызықтар

1. Геодезиялық сызықтың анықталуы. Беттегі қисық геодезиялық сызық деп аталады, егер әр нүктеде оның геодезиялық иілімі нөлге тең болса.

Геогдезиялық сызықтар беттің ішкі геометриясының объектісі болып табылатыны түсінікті. Жазықтықта геодезиялық сызықтардың - түзу екені белгілі. Беттегі геодезиялық сызықтарға беттегі түзудің табиғи аналогы ретінде қарауға болады. Геодезиялық сызықтың екі жай қасиеттерін белгілейік.

Кейбір қисығының біреуіне геодезиялық сызық болатын екі бет бір-біріне тура қиылысатын болса, онда ол басқасына да геодезиялық болады.

Шынында да, анықталғандай қисықтың геодезиялық иілімі жанама жазықтыққа қатысты вектордың иіліміне проекция болып табылады, жанама жазықтық тура 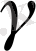екі бет үшін де бірдей.

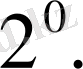
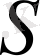бетіндегі 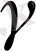қисығы геодезиялық сызық болуы үшін, беттің нормаліндеғі иілім нөлден өзге болғандағы 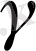қисығының әр нүктесіндегі бас нормалі 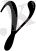-ға коллениар болуы қажетті және жеткілікті.