Комплекс айнымалы функцияларының туындылары, аналитикалық қасиеттері және конформдық бейнелеу


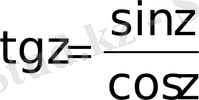 ;
;
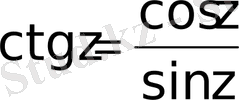
функциялары орындалады және барлық тригонометриялық формулалар орындалады:
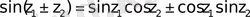 ;
;
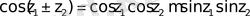 и т. д.
и т. д.
Гиперболалық функциялар нақты аргументтің функциялары тәрізді анықталады:
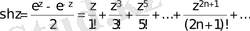 ;
;
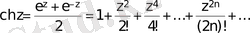 .
.
Бұлар тригонометриялық функциялармен былай байланысады:
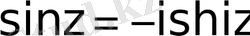 ;
;
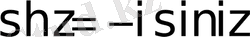 ;
;
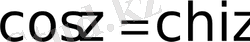 ;
;
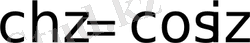 ;
;
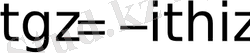 ;
;
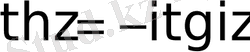 ;
;
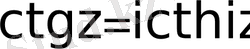 ;
;
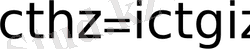 ;
;
(өздерің тексеріңдер) .
5
0
.
 функциялары сәйкес
функциялары сәйкес
 ,
,
 ,
,
 ,
,
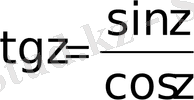 функцияларына кері функциялар ретінде анықталады, және де олардың бәрі де көп мәнді функциялар.
функцияларына кері функциялар ретінде анықталады, және де олардың бәрі де көп мәнді функциялар.
Дәлелдеңдер:
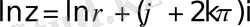 ,
,
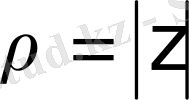 ,
,
 ,
,
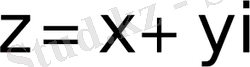 .
.
§14. 2 Комплекс айнымалылы функцияның туындысы
Z
облысының бір мәнді
 функциясын қарастырамыз.
функциясын қарастырамыз.
Анықтама.
Егер

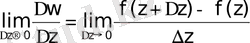 (2)
(2)
ақырлы шегі бар болса, онда ол шек
 функциясының туындысы деп аталады және былай белгіленеді:
функциясының туындысы деп аталады және былай белгіленеді:
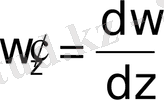
Бұл шек ∆ z -тің нөлге қалай ұмтылғанына тәуелсіз.
Анықтама.
Z
облысының
 нүктесінде үзіліссіз туындысы бар
нүктесінде үзіліссіз туындысы бар
 функциясы осы облыстың аналитикалық функциясы деп аталады.
функциясы осы облыстың аналитикалық функциясы деп аталады.
Шектің қасиеттері негізінде туындының негізгі қасиеттері шығады.
Қасиеттері:
- ,
- ,
- .
- Егер күрделі функциятүрінде берілсе, мұнда- комплекс айнымалы функция, және туындыларыменбар болса, онда мына формула орынды:
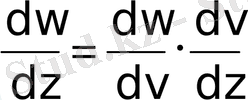 .
.
14. 2. Функциялардың туындыларының кестесі. 1.
 , мұндағы
n -
бүтін сан. Туындысын табамыз, ол үшін функцияның өсімшесін анықтаймыз:
, мұндағы
n -
бүтін сан. Туындысын табамыз, ол үшін функцияның өсімшесін анықтаймыз:
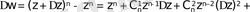
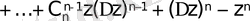 .
.
Сонда туынды мынаған тең:
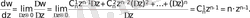 Көрсеткіштік және тригонометриялық функцияларды қарастырамыз:
Көрсеткіштік және тригонометриялық функцияларды қарастырамыз:
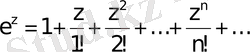 ;
;
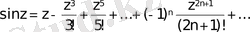 ;
;
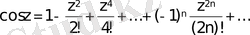 .
.
Бұл қатарлар
z-
ң кез келген мәндерінде жинақты,
 .
Осының негізінде бұл қатарларды дифференциалдауға болады.
.
Осының негізінде бұл қатарларды дифференциалдауға болады.
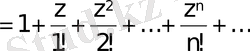 .
.
Оң бөлігі Маклорен қатарына дәл келеді (
 -ң жіктелуі) . )
-ң жіктелуі) . )
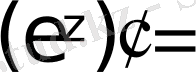
 .
.
Осы тәрізді қалған қатарларды да дифференциалдаймыз:
3.
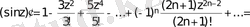
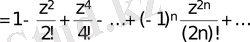 ; яғни
; яғни
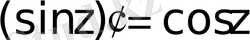 .
.
4.
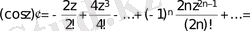
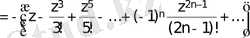 ; яғни
; яғни
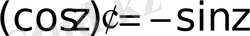 .
.
5.
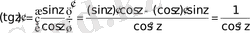 .
.
6.
 .
.
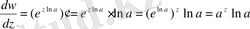 .
.
7.
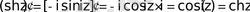 ,
,
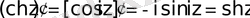 ;
;
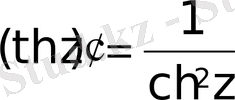 ,
,
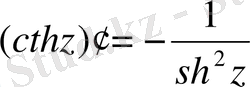 ,
,
(өздерің табыңдар) .
14. 2. 2 Нөлге тең емес туындының геометриялық кескіні. Комплекс сандар жазықтығын және оның Z нүктесін қарастырамыз.
z+∆z
y
0 x
Z облысының басқа z+∆z нүктесін аламыз. w=f(z) - функциясы осы Z жазықтығын басқа бір W жазықтығына бейнелейді, яғни z нүктесін → w нүктесіне,
z+∆z нүктесін → w+∆w- нүктесіне көшіреді.
v
w+∆w
w W
0 u
Туындысын қарастырамыз:
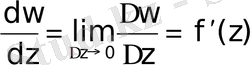 Equation. 3 .
Equation. 3 .
Шектер туралы негізгі теоремалар бойынша:
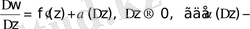 ақырсыз аз шама.
ақырсыз аз шама.
 ;
;
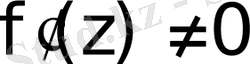 ;
;
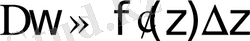 - функция өсімшесінің бас мәні.
- функция өсімшесінің бас мәні.
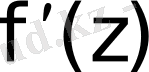 туындысын көрсеткіштік функция түрінде береміз:
туындысын көрсеткіштік функция түрінде береміз:
f ′(z) =re iϕ .
Бас мәнінің берілуінен мынаны аламыз:
∆w ≈ r∙ρe i(φ+θ) .
Функцияның өсімшесінің аргументі сол
θ
және кейбір
ϕ
бұрышы, ал ол
∆z-
ң аргументі болып табылады:
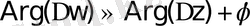 .
.
Анықтама. Егер Z облысының барлық нүктелерінде нөлден өзге үзіліссіз туындысы бар болса, онда бейнелеу конформдық деп аталады. Бұл бейнелеуде екі жатық қисық арасындағы бұрыш өзгермейді.
w=f(z) аналитикалық функциясы жәрдемімен орындалған бейнелеу конформдық болып табылады.
y
F 2
F 1
θ
z
- x
v
F′ 2
F′ 1
θ
w
- u
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz