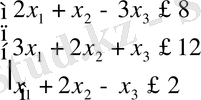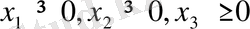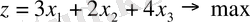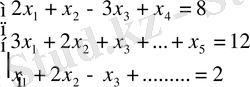Сызықтық және математикалық программалау: теориясы, шешу әдістері (симплекс, графиктік, Жордан) және оқу-әдістемелік қолданбалар


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:
1 Математикалық және Сызықтық программалаудың электронды оқулықтарыН пайдалану арқылы білім беру деңгейін көтеру
1. 1 Сызықтық программалау мәселелерін ақпараттандыру және талдау жолдары
Жалпы сызықтық программалау терминін шарттары сызықтық өрнектермен анықталған экстрималды есептерді шешу әдістері деген мағынада түсінеміз.
Көздеген мақсатқа жеткендікті дәлелдейтін белгіні оптималдық критерии (оптималық принціпі) деп атайды. Әдетте оптималдық критери ретінде «ең көп (максимум) пайда», «ең аз (минималды) шығын», «максилалды рентабельдік» т. б. қарастырылады.
Келесі кезеңде белгісіздерге қойылатын талаптар, яғни шарттар анықталады. Ол есеп шартындағы экономикалық және техникалық факторларға қатысты. Осылай анықталған шектеулер жиыны мәселенің шектеулер жүйесін құрайды.
Егер мақсат функциясы пайдалы экономикалық факторды мысалы, табыс, пайды, т. б. білдірсе оның максимум, яғни ең үлкен мәнін, ал зиянды факторды білдірсе, яғна критерий шығын болса, минимум мәнәі іздеу қажет болады. Сондықтан мәселе математикалық тұрғыда былайша тұжырымдалады: қойылған шектеулерді (шарттарды) толық қанағаттандырып, функционалдық ең үлкен немесе ең кіші мәнін қамтамасыз ететін белгісіздердің мәнін табу керек.
Сонымен, мәселенің тиімді шешімін табу есебінде көздеген мақсатқа жеткізетін
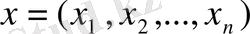 белгісіз шамаларын табу қажет.
белгісіз шамаларын табу қажет.
Белгісіздердің сан мәндерінің тізбегі жоспар деп аталады. Қойылған шектеулер жүйесін қанағаттандыратын кез келген жоспар жарамды жоспар деп аталады. Функционалға ізделінді максимум немесе минимум мәнін беретін мүмкін жоспар оптималды, яғни тиімді жоспар деп аталады. Демек қойылған экономикалық мәселені шешу жарамды шешімдердің ішінен оптимал шешімді табуды білдіреді. Барлық жарамды шешімдер математикалық программалу есебінің анықталу облысын құрайды.
Мәселенің мақсат функциясы мен шектеулер жүйесін белгісіз шамаларға қатысты сызықты (бірінші дәрежелі) болған жағдайда МП сызықты программалау деп аталады. Мағынасына сәйкес мұндай мәселені сызықтық оптимал мәселе деп атауға болады.
Ал егер мақсат функциясы немесе шектеулер жүйесінде белгісіздерге қатысты сызықты емес өрнек болса, онда сызықты емес программалау есебі анықталады.
Енді математикалық программалау әдістері мен шешілетін сызықтық оптималы мәселелерін қарастырайық.
Өндірісті тиімді жоспарталу мәселесі. Бұл практикада кең таралған мәселердің бірі; шектеулі өндіріс қорларын ұтымды пайдаланып, максималды өнім өндіруді жоспарлауды көздейді. Бұл есептің мазмұны мынада:
Кәсіпорын m түрлі ресурс (мысалы, егістік, жұмысшы қолы, дән, жанар-жағармай, жем-шөп, т. б. ) қолданып, n түрлі өнім өндіреді делік в 1 , в 2 , . . . , в m әрбір ресурстың кәсіпорында бар мөлшері. Әрбір өнімнің бірлік мөлшерін сатудан түсетін таза пайда-c 1 , c 2 , …, c n және әрбір өнімнің бірлігін өндіруге жұмсалатын әрбір ресурсың мөлшері- a 11 , a 12 , …, a 1n , a 21, a 22 , …, a ij , …, a mn -белгілі, мұндағы a ij -j-ші өнімнің біреуіне жұмсалатын i-ші ресупс мөлшері (i=1, …, m, j=1, …, n) . Бұл санлар технологиялық коэффиценттер деп аталады.
Кәсіпорындардағы бар ресурстарды ұтымды пайдалану арқылы максимум пайда беретін өндірістің оптимал жоспатын Х, яғни әрбір өнім мөлшерін х 1 , х 2, . . . , x n табу керек.
Есептің математикалық моделін құру үшін өндіру қажет өнімдердің шамаларын х j (j=1, …, n) арқылы белгіледік.
Сонда барлық өнімдерді сатуден түсетін пайда
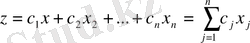
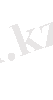
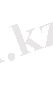
формуласы арқылы өрнкетеледі. Мәселенің қойылымы бойынша пайданың максимал мәнін табу көзделеді, демек
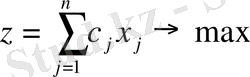
Өнімдерді өндіруге жұмсалатын ресурыстардың мөлшері қолда бар мөлшерінен аспау тиіс, яғыи мақсат функциясына максимал мән меншіктеитін белгісіздер келесі шектеулерді қанағаттандыруы тиіс:
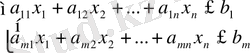
Эканомикалық мағынасына сәйкес әрбір белгісіз шама теріс сан болуы мүмкін емес, демек олар
x 1 ≥0, …, xn≥0 шарттарын қанағаттандырулары тиіс.
Мал азығының рационын құру мәселесі
[1] Шаруашылықта дайын n-түрлі мал азығы бар делік. Әр азақтың құрамында m - түрлі қоректі элементтері бар. Бір азақ өлшемінің i-элемен нормасы -
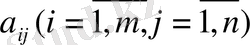 және бір азақ өлшемінің өзіндік құны -
және бір азақ өлшемінің өзіндік құны -
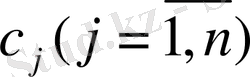 белгілі. Рационда әрбір қоректік элемент мөлшері Р
і
шамасынан кем болуға тиісті. Осы шартқа сәйкес зоотехниклық нормаларға сай нормаларға сай келетін өзіндік құны өте арзан рацион құру керек.
белгілі. Рационда әрбір қоректік элемент мөлшері Р
і
шамасынан кем болуға тиісті. Осы шартқа сәйкес зоотехниклық нормаларға сай нормаларға сай келетін өзіндік құны өте арзан рацион құру керек.
Есептің математикалық моделін құру үшін рационға кіретін азықтарды
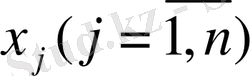 арқылы белгілейік, рационның өзіндік құны z
арқылы белгілейік, рационның өзіндік құны z
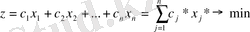 арқылы жазылады.
арқылы жазылады.
Рацион құрамындағы әрбір қоректік заттардың шамасы нормадан кем болмауы
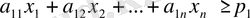

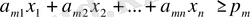
шектеулер жүйесі арқылы жазылады.
Айнымалылардың теріс сан болмау талабы
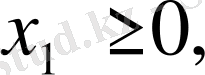 Equation. 3
Equation. 3
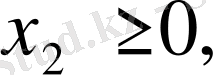 Equation. 3 …,
Equation. 3 …,
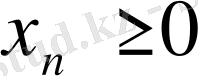 Equation. 3
Equation. 3
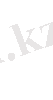 Equation. 3 .
Equation. 3 .
Сонымен,
мақсат
: анықталған барлық сызықтық шектеулерді қанағаттандырып z функциясының ең кіші мәнін қамтамасыз есетін x=
 мәндерін табу.
мәндерін табу.
Сонымен математикалық программалау мәселелерінің ішінде сызықтық оптимал мәселелер барынша және терң зерттелген жаңа тиімді шешу әдісі анықталған ерекше мәселелер класы болып табылады.
Жалпы сызықты оптимал мәселелер дер Евклид кеңістігіндегі сызықтық функциялар арқылы анықталған ең үлкен және ең кіші мәнін қамтамасыз ететін нүктесін табу есебін айтады.
Сызықтық оптимал мәселелер теориясының жалпы есебі қысқаша төмендегіше жазылады:
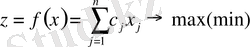 (1. 1)
(1. 1)
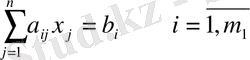 (1. 2)
(1. 2)
 (1. 3)
(1. 3)
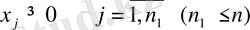 (1. 4)
(1. 4)
мұндағы
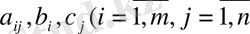 ) берілген сандар. Экономикалық мазмұнына сәйкес
) берілген сандар. Экономикалық мазмұнына сәйкес
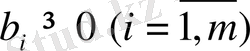 . Егер
. Егер
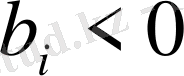 болса і-ші шектеуінің екі жағын да (-1) -ге көбейту керек.
болса і-ші шектеуінің екі жағын да (-1) -ге көбейту керек.
Сызықтық оптимал мәселерер (СОМ) есебінде мақсан функциясының максимумын табуда оның минимумын табуға, және керісінше, минимумын табуды оның максимумын іздеуге түрлендіруге болады, себебі
 және
және
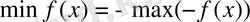 .
.
Көптеген экономикалық есептерде берілгендер х
1
, . . . , х
n
техниканың станоктардың, т. б. бүтін объектілердің санын білдіреді, мұнда есептің шешімі бүтін сандардан тұруы керек. Сондықтан көптеген СОМ-лерде белгісіздерге қосымша бүтін сан болу шарты -
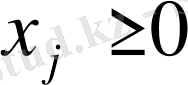 және бүтін қойылады. Мұндай мәселелерді бүтін мәнді СОМ-лер (бүтін мәнді сызықты программалау) немесе дискретті СОМ-лер деп атайды.
және бүтін қойылады. Мұндай мәселелерді бүтін мәнді СОМ-лер (бүтін мәнді сызықты программалау) немесе дискретті СОМ-лер деп атайды.
Енді СОМ теориясында қолданылатын бірнеше маңызды анықтамаларды қарастырайық.
1-анықтама. Оптималдық критерий ретінде алынған (1. 1) сызықты функциясы - мақсат функциясы , (1. 2) - (1. 3) шарттары - есептің шектеулері, ал (1. 4) - белгісіздердің теріс емес шарттары деп аталады.
2-анықтама. (1. 3) - (1. 4) шарттары бойынша (1. 1) мақсат функциясының максимум мәнін анықтау есебі СОМ -лердің стандартты (симметриялық) есебі деп аталады. (m 1 =0, n 1 =n) .
3-анықтама. (1. 2) - (1. 4) шарттары бойынша (1. 1) мақсат функциясының максимум мәнін анықтау есебі СОМ-лердің канондық есебі деп аталады. (m 1 =m, n 1 =n)
4-анықтама.
(1. 1) - (1. 4) шарттарын қанағаттандыратын Х=
 сандары СОМ-сінің жарамды шешімі (жоспары) деп, ал мақсан функциясының максимум немесе минимум мәнін қамтамасыз естетін Х
*
=(
сандары СОМ-сінің жарамды шешімі (жоспары) деп, ал мақсан функциясының максимум немесе минимум мәнін қамтамасыз естетін Х
*
=(
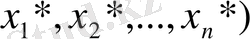 -
оптимал жоспар
деп аталады.
-
оптимал жоспар
деп аталады.
Келтірілген үш турлі есеп (жалпы, симметриялық, канондың) белгілі бір мағынада өзара эквивалентті, яғни СОМ-сінің кез келген түріндегі есебін басқа түріне оңай түрлендіруге болады.
Жалпы есепті канондық түрге келтіру үшін теңсіздіктерге қосымша теріс емес
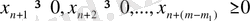 айнымалалары енгізіледі. Сонда шектеулер теңдіктермен өрнектеледі:
айнымалалары енгізіледі. Сонда шектеулер теңдіктермен өрнектеледі:
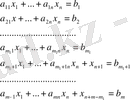
Егер
 болса, онда есеп канондық түрге толыұ түрленген, ал
болса, онда есеп канондық түрге толыұ түрленген, ал
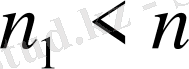 жағдайында, яғни
жағдайында, яғни
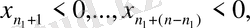 есепті канондық түрге ауыстыру үшін
есепті канондық түрге ауыстыру үшін
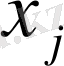 айнымалысын
айнымалысын
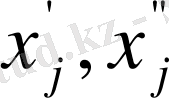 -теріс емес айнымалылардың айырмасымен ауыстырса болады.
-теріс емес айнымалылардың айырмасымен ауыстырса болады.
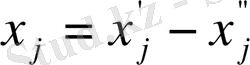 мұндағы
мұндағы
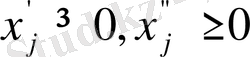
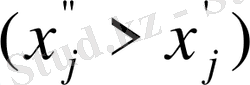 .
.
Енді берілген есепті канондық түрде жазуға мысалдар қарастырайық.
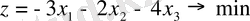
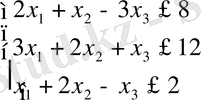
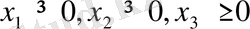
Канондық түрі:
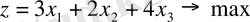
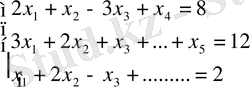
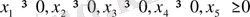
1. 2-мысал.
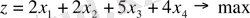
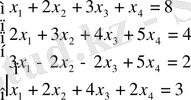
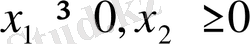
Канондық түрі:
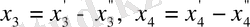
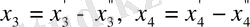 белгілеулерін жасау арқылы
белгілеулерін жасау арқылы
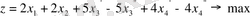
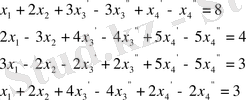
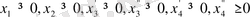
Қазіргі кезеңде СОМ-рді шешуді ең көп қолданатын әдістерінің бірі-симплекс әдісі. Ол алғашқы бір анықталған тірек шешімі деп аталатын жоспардан саны шектеулі алгебралық түрлендірулер арқылы оптимал шешімге детуге негізделген. Симпллекс әдісі канондық есепті шешуге арналған. m қатар, n бағанадан тұратын
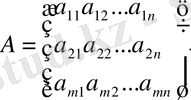 матрицасының жолдары n өлшемді вектр да, бағандары m өлшемді вектор болады.
матрицасының жолдары n өлшемді вектр да, бағандары m өлшемді вектор болады.
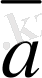 =(а
1,
а
2
, . . . , а
n
) және
=(а
1,
а
2
, . . . , а
n
) және
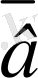 =(
в
1,
в
2
, . . . ,
в
n
) векторлары сәйкес компонеттері тең болған жағдайда ғана . a
j
=
в
j
, (j=1, 2, . . . n) өзара тең вектор деп есептеледі.
=(
в
1,
в
2
, . . . ,
в
n
) векторлары сәйкес компонеттері тең болған жағдайда ғана . a
j
=
в
j
, (j=1, 2, . . . n) өзара тең вектор деп есептеледі.
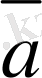 және
және
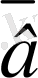 векторларының қосындысы деп
векторларының қосындысы деп
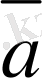 +
+
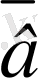 =(а
1,
+
в
1,
а
2
+
в
2
, . . . , а
n
+
в
n
) анықталған вектор аталады.
=(а
1,
+
в
1,
а
2
+
в
2
, . . . , а
n
+
в
n
) анықталған вектор аталады.
n өлшемді кеңістікте нөлдік вектор мен i-орта векторлары ерекше орын алады. Нөлдік вектордың барлық компонеттерінөлге тең :
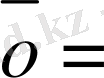 (0, 0, . . . , 0), оның геометриялық мағынасы координаттар бас нүктесі. Әрине,
(0, 0, . . . , 0), оның геометриялық мағынасы координаттар бас нүктесі. Әрине,
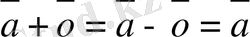 .
.
i-орт
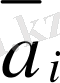 i-ші ортасында ғана 1 болып, қалған компонеттері нөл болатын вектор:
i-ші ортасында ғана 1 болып, қалған компонеттері нөл болатын вектор:
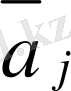 =(0, . . . , 0, 1, 0, . . . , 0) . Геометриялық тұрғыда i-орт-i-ші остің бойындағы онымен бағыттас бірлік вектор.
=(0, . . . , 0, 1, 0, . . . , 0) . Геометриялық тұрғыда i-орт-i-ші остің бойындағы онымен бағыттас бірлік вектор.
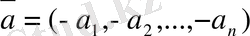 векторларға
векторларға
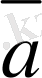 векторына қарамы-қарсы вектор деп аталады, бұдан
векторына қарамы-қарсы вектор деп аталады, бұдан
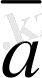 +(-
+(-
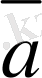 ) =
) =
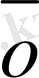 екендігі айтпаса да түсінікті.
екендігі айтпаса да түсінікті.
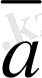 +
+
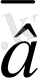 =
=
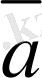 +(-
+(-
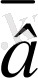 ), яғни бір вектордан екінші векторды алу бірінші векторға екінші векторға қарама-қарсы векторды қосқанмен бірдей.
), яғни бір вектордан екінші векторды алу бірінші векторға екінші векторға қарама-қарсы векторды қосқанмен бірдей.
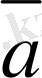 векторының λ санына көбейтіндісі деп λ
векторының λ санына көбейтіндісі деп λ
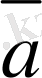 =(
=(
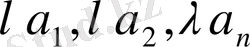 ) арқылы анықталған векторларды айтады, Бұдан төмендегі теңдіктер шығады:
) арқылы анықталған векторларды айтады, Бұдан төмендегі теңдіктер шығады:
λ(
±
) =λ
±λ
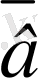
(k±λ)
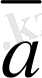 =k
=k
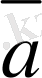 ±λ
±λ
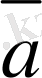
k(λ
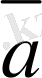 ) =(k λ)
) =(k λ)
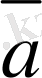
Мұның салдары: 0*
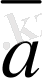 =0 (-1) *
=0 (-1) *
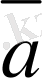 =-
=-
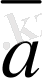 , λ*
, λ*
 =
=
 .
.
Векторлық алгебрада екі вектордың скаляр көбейтіндісі деп анықталған: екі вектордың скаляр көбейтіндісі деп сәйкес компонеттердің көбейтінділерінің қосындысыны тең сан аталады:
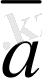 +
+
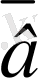 =а
1
в
1
+а
2
в
2
+, . . . , +а
n
в
n.
=а
1
в
1
+а
2
в
2
+, . . . , +а
n
в
n.
Мысылы,
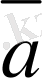 =(1, 3, 7, 12),
=(1, 3, 7, 12),
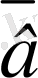 =(2, 4, 1, 0) векторларының скаляр көбейтіндісі
=(2, 4, 1, 0) векторларының скаляр көбейтіндісі
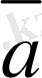 *
*
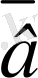 =1*2+3*4+7*1+12*0=21
=1*2+3*4+7*1+12*0=21
Сондай ақ
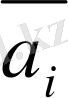 *
*

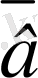 = а
1
*0+а
2
*0+ . . . , +а
n
+*0=0
= а
1
*0+а
2
*0+ . . . , +а
n
+*0=0
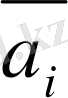 *
*
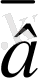 = 0*
в
1
+0*
в
2
+ . . . , +1*
в
i
+…+0*в
n
=
в
i
= 0*
в
1
+0*
в
2
+ . . . , +1*
в
i
+…+0*в
n
=
в
i
*
=a 1 2 +a 2 2 +…+a n 2
Векторлардың ұзындығы
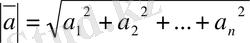 формуласын ескерсек
формуласын ескерсек
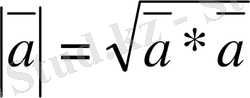
жалпы а
1
х
1
+а
2
х
2
+, . . . , +а
n
х
n. =
в
түріндегі сызықтық теңдаудің сол жағын
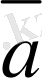 = (а
1,
а
2,
. . . , а
n
)
= (а
1,
а
2,
. . . , а
n
)
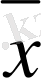 = (
х
1
,
х
2
, . . . , х
n
) векторларының скаляр көбейтіндісі деп түсінуге болады:
= (
х
1
,
х
2
, . . . , х
n
) векторларының скаляр көбейтіндісі деп түсінуге болады:
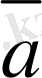 *
*
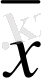 =
в
=
в
3-анықтама:
Егер
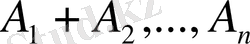 векторлар үшін
векторлар үшін
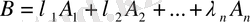 теңдігі орындалатын
теңдігі орындалатын
 сандары табылса В векторы
сандары табылса В векторы
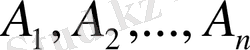 векторларының сызықтық комбинациясы деп аталады.
векторларының сызықтық комбинациясы деп аталады.
4-анықтама:
Егер
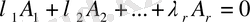 нөлдік комбинациясы
нөлдік комбинациясы
 болғанда ғана орындалса,
болғанда ғана орындалса,
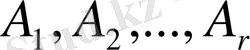 векторларының сызықтық тәуелсіз векторлар деп атайды, кері жағдайда, яғни кемінде бір нөлден өзге
векторларының сызықтық тәуелсіз векторлар деп атайды, кері жағдайда, яғни кемінде бір нөлден өзге
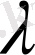 саны табылса
саны табылса
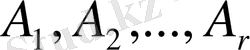 векторлары сызықтық тәуелді векторлар деп аталады.
векторлары сызықтық тәуелді векторлар деп аталады.
Мысылы, А 1 =(2, 4, 3), А 2 =(2, 3, 1), А 3 =(5, 3, 2, ), А 4 =(1, 7, 3) векторлары сызықтық тәуелді, себебі А 1 +2А 2 -А 3 -А 4 =0.
5-анықтама: n өлшемді векорлық кеңістіктің кезкелген векторын осы кеңістіктің базистік векторлардың сызықтық комбинациясы арқылы өрнектеуге болады.
Е 1 =(1, 0, …, 0), Е 2 =(0, 1, 0, …, 0), . . . , Е n =(0, 0, …, 0, 1) - бірлік векторлар жүйесі n өлшемді векторлық кеңістіктің базисі бола алады.
Жиын тұйық болса тура шектелмеген, және керісінше, шектелген жиын болса тура тұйық емес болуы мүмкін.
Жазықтықтағы барлық нұктелері бар қабырғасы арқылы жүргізілген түзудің бір жағына тиісті көпбұрыштар дөңес тұйық шектелген жиын болады. Мұндай көпбұрыштың төбелері шеткі, яғни бұрыштық нүкте болып табылады.
Вейерштрасс теоремесы. Егер f(
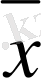 ) функциясы Х тұйыұ шектелген жиынында анықталған және үздіксіз болса, онда бұл функция осы жиында глобальды максимум және глобальды минимумына ие болады.
) функциясы Х тұйыұ шектелген жиынында анықталған және үздіксіз болса, онда бұл функция осы жиында глобальды максимум және глобальды минимумына ие болады.
Енді сызықтық программалауды қолданылатын математикалық аппарат негізін құрайтын алгебралық түрлендірулерді қарастырайық.
Сайып келгене, оқыту курстарын құру білімді дамытып, ақпараттандыру процессін шыңдай түседі.
Әдістемелік жүйенің функционалдық мүмкінділіктері туралы төменде айтып өтеміз.
Біз алдынғы бөлімдерде сызықтық программалау әдістерінің тек теориялық мүмкіндіктерін ғана қарастырған болатынбыз, енді осы программалау әдістерін қолдану арқылы шығарылған есептерге мысалдар келтіреміз.
Сызықтық программалау есептерін шешуге арналған визуалды зертханалық жұмыстар әдістемелік жүйе ретінде қарастырылған.
Мысал 1. Сызықтық программалау мәселесін жазу жолдары. Сызықтық оптимал мәселелер теориясының жалпы есебін орандауға берілген мысал.
Төмендегі берілген есепті канондық түрде жазуға мысалдар қарастырайық.
1-мысал:
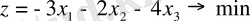
Канондық түрі:
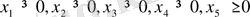
Мысалы 2. Сызықтық теңдеулер жүйесін Жорданның біртіндеп кеміту әдісімен шешуге арналған мысал.
Төменде берілген теңдеулер жүйесін шешу керек:
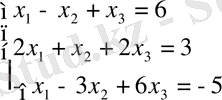
Шешуі. Алдымен алғашқы Жордан кестесін құрастырамыз:
Кесте 3. 1. Жордан кестесі
Кесте 3. 1 ге Жордан түрлендіруін қолданып кесте 3. 2 ге өтеміз; шешуші элемент а 11 =1≠0 (r=1 -шешуші жол, s=1-шешуші бағана) . Демек х 1 белгісізін базиске енгіземіз:
Кесте 3. 2. Түрленген Жордан кестесі
Кестедегі базиске енгізілген айнымалының мәнін оған сәйкес қатардағы коэффицентерін кестенің төбесіндегі көрсеткіштерге көбейтіп есептейтін бағаналардан нөлдік бағаналарды ерекшелеуге, яғни сызып тастауға болады.
Кесте 3. 2 ден шешуші эемент а 22 =3≠0 (r=2 -шешуші қатар, s=2-шешуші бағана) таңдап, түрлендіру арқылы үшінші кестеге өтеміз:
Кесте 3. 3. Түрленген Жордан кестесі
Бұл кестеден шешуші элемент а 3 =7≠0 арқылы түрлендіру соңғы кестені береді
Кесте 3. 4. Түрленеген соңғы кесте.
Сонымен берілген теңдеулер жүйесінің шешімі х 1 =2*1=2, х 2 =-3*1=-3, , х 3 =1*1=1 немесе шешім 1- бағанадағы мәндер.
Мысал 3. Сызықтық программалау есебін шешудің графиктік тәсіліне арналған екі өлшемді кеңістікте(жазықтықта) берілген есепті шығару.
Екі өнімді өндіруге жұмсалатын ресурс мөлшері мен өнімдердің біреуін сатудан пайда соммасы төмендегі кестеде берілген.
Кесте 3. 4. Екі өнімнің ресурс қоры.
А
В
5
4
2
4
20
36
Максимум пайда түсетін өндіріс жоспарын анықтау керек.
Шешуі: Есептің математикалық моделін құру берілгендер енгіземіз: х 1 -өндірілетін бір өнім мөлшері, х 2 -екінші өнім мөлшері. Сонда мақсат функциясы - пайда:
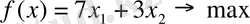
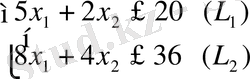
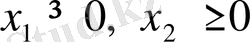
Максимум пайда беретін х 1 , х 2 шамаларын табудың графиктік жолы.
а) Есептің мүмкін шешімдер жиынын анықтаймыз:
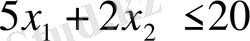 және
және
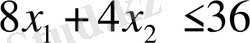 ,
,
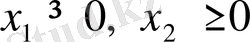 жарты жазықтығын саламыз, орардың қылысуы ОАВС-тұйық шектелген көпбұрыш (сурет 3. 1. )
жарты жазықтығын саламыз, орардың қылысуы ОАВС-тұйық шектелген көпбұрыш (сурет 3. 1. )
Сурет 3. 1. Жазықтықтағы салынған тұйық көпбұрыш
ә) Графикте
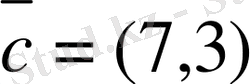 векторын анықтаймыз.
векторын анықтаймыз.
б)
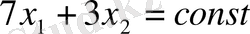 немесе
немесе
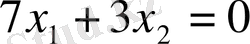 түзуін саламыз. Бұл түзу (0, 0) , (3, 7)
түзуін саламыз. Бұл түзу (0, 0) , (3, 7)
нүктесі арқылы өтеді.
в) Максимум f(x) анықтау үшін (f) түзуін
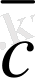 векторының бағытымен оңға қарай өзіне параллель жылжытамыз, оны шешімдер жиынымен соңғы ортақ нүктесі -В нүктесі.
векторының бағытымен оңға қарай өзіне параллель жылжытамыз, оны шешімдер жиынымен соңғы ортақ нүктесі -В нүктесі.
г)
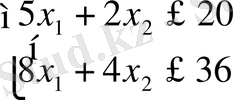 теңдеулер жүйесін шешу арқылы х
1
=2, х
2
=5 В нүктесінің координаттарын табамыз: В(2, 5) . Сонымен ең көп пайда табу үшін х
1
=2, х
2
=5 мөлшерінде өнім өндіру керек,
теңдеулер жүйесін шешу арқылы х
1
=2, х
2
=5 В нүктесінің координаттарын табамыз: В(2, 5) . Сонымен ең көп пайда табу үшін х
1
=2, х
2
=5 мөлшерінде өнім өндіру керек,
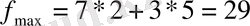 (ақша бірлігі) .
(ақша бірлігі) .
Мысал 4. Сызықтық оптимал мәселені Симплекс әдісімен шешу. Алғашқы бір анықталған тірек шешім деп аталатын жарамды жоспардан бірнеше алгебралық түрлендірулер арқылы оптимал шешімге жету
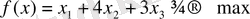
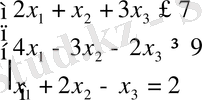
 ,
,
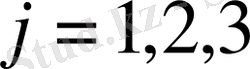 ,
,
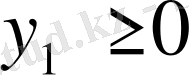 ,
,
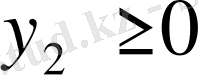 енгізу арқылы есепті канондық түрге түрлендіреміз:
енгізу арқылы есепті канондық түрге түрлендіреміз:
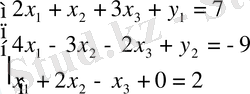
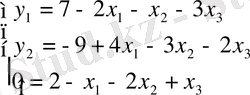
Кесте 3. 5. Алғашқы симплекс-кесте
TA
БА
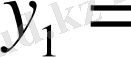
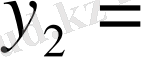
1-итерация; 1-алгоритм. 1-саты бойынша 3-қатарда нөлдік элемент бар
 ,
,
 ,
,
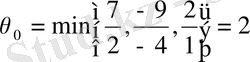 , демек
, демек
 ,
,
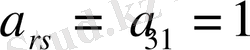 .
.
Кесте 3. 6. Екніші симплекс-кесте.
TA
БА
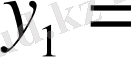
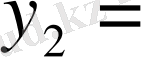
немесе нөлдік бағанды есепке алудың қажеті жоқ. Жоғарыдағы кестені шешу арқылы келесі кестені аламыз.
Кесте 3. 7. Үшінші симплекс -кесте.
TA
БА
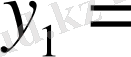 Equation. 3
Equation. 3
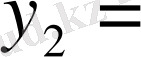 Equation. 3
Equation. 3
2-итерация .
1-саты. Базистік айнымалы бағанасында нөлдік қатар жоқ, 2-алгоритмге көшеміз.
1-итерация.
2-алгоритм.
1-саты бойынша бос мүше бағанасында -1<0, (t=2), демек Х=(2, 0, 0, 3, -1) жоспары - жарамсыз жоспар.
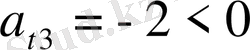 , демек есептің шешімі бар: шешуші бағана
, демек есептің шешімі бар: шешуші бағана

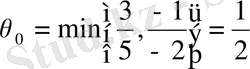 , демек
, демек
 ,
,
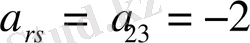 . Келесі кестені анықтайық.
. Келесі кестені анықтайық.
Кесте 3. 8. Төртінші симплекс -кесте.
TA
БА
 Equation. 3
Equation. 3
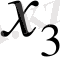 Equation. 3
Equation. 3
2-итерация . 2 алгоритм.
Бос мүше бағанасында теріс элемент жоқ, Х=(2, 5, 0, 0, 5, 0, 5, 0) - алғашқы тірек жоспары. Енді оптимал жоспарды анықтаймыз.
1-итерация . 3 алгоритм.
1-саты бойынша Ғ-қатарда екі теріс элемент: -24 және -2 бар -24<-2, демек
 (Х
2
- базиске енді),
(Х
2
- базиске енді),
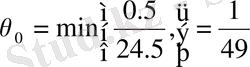 , демек
, демек

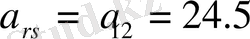 . Енді келесі кестені анықтаймыз.
. Енді келесі кестені анықтаймыз.
Соңғы кестеде Ғ-қатарда теріс элемент жоқ, демек
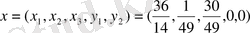 - оптимал шешім, және оптимал жоспар - жалғыз, себебі Ғ - қатарда ешбір нөл жоқ.
- оптимал шешім, және оптимал жоспар - жалғыз, себебі Ғ - қатарда ешбір нөл жоқ.
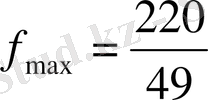 .
.
Кесте 3. 9. Бесінші симплекс -кесте.
TA
БА
1. 3. Сызықтық оптимал мәселелердің қарапайым математикалық модульдерін құру
Сызықтық теңдеулер жүйесін Жорданның біртіндеп кеміту әдісімен шешу.
n белгісізді m сызықтық теңдеулер жүйесі берілсін:
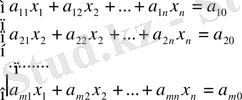
Берілген жүйені нөлдік теңдеулерарқылы қайта жазып
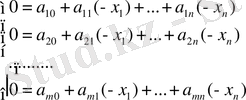
Жордан кестесі арқалы көрсетейік:
Кесте 1. Жордан кестесі
0=
0=
---
0=
…
0=
a 10
a 20
---
a r0
…
a m0
a 11
a 21
---
a r1
…
a m1
a 12
a 22
a r2
…
a m2
…
…
---
…
…
…
a 1j
a 1j
---
a rj
…
a mj
…
…
---
…
…
…
a 1s
a 2s
---
a rs
…
a ms
…
…
---
…
…
…
a 1n
a 2n
---
a rn
…
a mn
Әдістің мағынасы: кесте 1-де а rs ≠0 элементін таңдап, оның шешуші элемент деп атаймыз, сонда r-қатар-шешуші жол, s-бағана -шешуші бағана деп аталады. Одан кейін төмендегі тәртіп бойынша 1-кестені келесі кестеге түсіреміз.
- Шешуші элемент өзіне кері шамамен ауыстырылады:.
- Шешуші қатардың қалған элементтері шешуші элементке бөлінеді:
- Шешуші бағананың қалған элементтері шешуші элементке бөлініп, қарама-қарсы таңбаман жазылады:
- Кестенің қалған есептеледі (i≠r, j≠s)
Бұл амалдар Жорданның жетілдірілген тұрлендіруі (ЖЖТ) деп аталады. Алғашқы r түрлендіруден кейінгі кесте кесте 2 арқылы көрсетілген, әр түрлендіруде x s белгісізі r-қатардағы 0 мен орын ауыстырады(r<n) . [1]
Кесте 2. Түрленген Жордан кестесі
х 1 =
…
х r =
0=
…
0=
в 10
…
в r0
в r+10
…
в m0
в 11
…
в r1
в r+11
…
в m1
…
…
…
…
…
…
в 1r
…
в rr
в r+1r
…
в mr
в 1r+1
…
в rr+1
0
…
0
…
…
…
…
…
…
в 1n
в rn
---
0
…
0
Кесте 2 ден
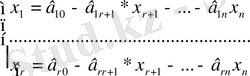
түріндегі жалпы шешімді табамыз, мұндайда берілген жүйе анықталмаған жүйе деп аталады және шексіз көп шешімі бар.
Мұндағы х 1 , . . . , х r - айнымалылары базистік, х r+1 , . . . , х n - тәуелсіз айнымалылар деп аталады. Егер тәуелсіз айнымалыларға нөл меншіктесек базистік шешім деп аталатын дербес шешім аламыз:
х 1 =в 10, х 2 =в 20 , . . . , х r =в r
Теріс емес базистік шешім сызықтық программалау теориясында ерекше орын аладыжәне тірек шешім деп аталады.
Кесте 2-де r=n болса берілген жүйенің бір ғана шешімі бар
3. 2. Өзіндік қолданыстағы алгоритм.
Бірінші өзіндік қолданыстың алгоритмі деп - өзіне өзі қолданылатын алгоритмді айтамыз. Бірақ та бұл корректірлі анықтама емес, себебі МҚА не сөздер ғана кіреді, Ал МҚА ондайға жатпайды. Сондықтан да бұл анықтаманы корректілі ету үшін, МҚА - дегі сызықты сызу керек. Бұл үшін алгоритмге жазба сөзі енгізіледі. МҚА - нің жазбасы деп - тізбектелген нүкте, үтір арқылы жазылған формалар жатады. Осылай бола тұра нүкте мен үтір формулаға енбейді. Мысалы келесі алгоритм:
#a → # (1) a → b (4) (1)
H1 #
 (2) H2 b → bb (5)
(2) H2 b → bb (5)
→ # (3)
Мұнда H1 алгоритмі сөз болып табылады.
#a→#; #
 ; → #
(2)
; → #
(2)
H2 алгоритм жазбасы - сөз.
a→b; b →bb (3)
Бір сөз алгоритм сөзінің жазбасын анықтайды немесе керісінше. Алгоритм жазбасы сз болғандықтан, оны алгоритм шығаруына қолданылады. Нәтижесінде келесі өздік қолданыстағы алгоритмнің корректілі анықтамасын аламыз. Өзіндік қолданыстағы алгоритм деп атаймыз егер де ол өзінің жазбасына қолданылса. Мысалы H1 өзіндік қолданыстағы алгоритмі өз жазбасымен жұмыста шығу сөзі ретінде бастайды және тоқтаумен аяқтайды:
1 2
#a→#; #
 ; →# → #→#; #
; →# → #→#; #
 ; →#
; →#
 →#; #
→#; #
 ; →#
(4)
; →#
(4)
H2 өзіндік емес алгоритмі ол өзінің жазбасында ғана жұмыс істейді.
4 5 5 5
a→b; b→bb; → b→b; b→bb → bb→b; b→bb → bbb→b; b→bb → … (5)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz