Жартылай өткізгіштердің зоналық теориясы және электр өткізгіштігінің эксперименттік-теориялық зерттелуі


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:
ЖОСПАР
Кіріспе.
І- тарау. Жартылай өткізгіштердің зоналық теориясы.
1. 1. Қатты денелердің зоналық теориясы
1. 2. Жартылай өткізгіштер
1. 3. Жартылай өткізгіштердің меншікті өткізгіштігі
1. 4. Жартылай өткізгіштердің қоспалы өткізгіштігі
Қорытынды.
Пайдаланған әдебиеттер тізімі.
Кіріспе
“Жартылай өткізгіштердің электр өткізгіштігін зерттеу ” тақырыбында жазылған дипломдық жұмыста қазіргі заманымызға сай, ғылым мен техниканың даму жағдайына байланысты, радиоэлектроникада қажетті ғылыми жұмыстар жасалған.
Бәрімізге белгілі, жартылай өткізгіштерсіз электротехникалық құралдардың алға басуы мүмкін емес, осыған байланысты дипломдық жұмысты осындай тақырыпта таңдау, автордың ғылымға деген құштарлығы барын көрсетеді.
Қазіргі кезде жартылай өткізгіштерді оптикалық тәсілдермен зерттеу ең тиімді тәсіл. Себебі бұл тәсіл арқылы электрондардың, кемтіктердің коллективті әсерлесуінен көп мағұлмат алады. Сонымен бірге бұл тәсіл арқылы жартылай өткізгіштердің зоналық құрылыстарын және жартылай өткізгіштердің электрофизикалық қасиеттерін зерттеп, бұл зерттеген қасиеттерді практикада қолдануда үлкен орын алады.
Жартылай өткізгіштер көбіне қатты денелерден және химиялық қоспалардан тұрады. Осыған байланысты олардың құрылысы күрделі болып келеді. Жартылай өткізгіштер құрылысына қарай металдың да, диэлектриктің де қасиеттерін көрсете алады. Металдарда температура өскенде, кедергісі артады, ал жартылай өткізгіштерде керісінше азаяды. Міне сол сияқты жартылай өткізгіштердің электр өткізгіштігіде металдардан өзгеше. Жартылай өткізгіш сыртқы электр өрісінде болса, осы өріс әсерінен еркін электрондар өріске қарсы бағытта қозғалады, екінші жағынан жылулық қозғалыс әсерінен кейбір электрондар өріске қарсы қозғалады. Жалпы келгенде электрондар өрістің әсерінен реттелген қозғалысқа түсіп, дрейфтік қозғалыс жасайды, жартылай өткізгіш арқылы электр өрісі бағытында еркін электрондар тобы азаяды. Негізінде қоспасы жоқ таза жартылай өткізгіштерде электронның және кемтіктік электр өткізгіштік жүзеге асады. Осыған байланысты жартылай өткізгіштерде электр тоғы екі құраушымен бірдей бағытталған электрондық және кемтіктік токтармен анықталады. Кейбір жартылай өткізгіштердің электр өткізгіштігін энергетикалық ұғымдармен түсіндіруге болады.
Айтылған фактілерді ескере отырып дипломдық жұмыста жартылай өткізгіштердің электр өткізгіштігін эксперименттік және теориялық зерттеулер жүргіздік. Ол үшін бірнеше шетелдік әдебиеттерді қарастырдық. Қарастырылғын эксперименттік жұмыстарды мұхият зерттеп, теориялық есептеулермен салыстырдық. Дипломдық жұмыста теориялық жолмен есептелген графиктер келтірілген. Қорыта айтқанда теориялық жолмен есептелген нәтижелер эксперименттік нәтижелермен сәйкес келіп отырды.
I-тарау
ЖАРТЫЛАЙ ӨТКІЗГІШТІҢ ЗОНАЛЫҚ ТЕОРИЯСЫ
2. 1. Қатты денелердің зоналық теориясы
Кристалдың энергиялық зоналары кристалдағы еркін электрондарға жақын валенттік электрондардың энергиясы квазиүздіксіз өзгеретінін байқаймыз. Бұл рұқсат етілген зонаның энергиясының спектрі көптеген жақын орналасқан дискретті деңгейлерден тұратынын көрсетеді. Шын мәнісінде кристалдың валенттік электрондары еркін қозғалып жүрмейді. Оларға тордың өрісі периодты түрде әсер етеді. Бұл жағдай валенттік электрондардың энергиясының мүмкін деген мәнінің спектрі бір қатар ауысып отыратын рұқсат етілген және тыйым салынған зоналарға жіктеледі деген пікірге келтіреді (1. 1-сурет) . Рұқсат етілген зоналар шегінде энергия квазиүздіксіз өзгереді. Ал тыйым салынған зоналарға тиісті энергияның мәндері іске асырылмай қалады. [1] .
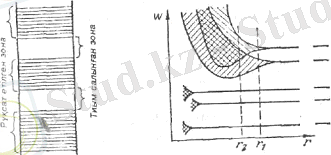
1. 1 - сурет 1. 2- сурет
Зоналардың пайда болуын түсіну үшін атомдардың кристалға бірігу процесін көз алдымызға келтірейік. Айталық, әуелде кез-келген заттың N жекеленген атомдары бар болсын. Атомдар бір-бірінен жекеленіп тұрғанда, олардың энергиялық денгейлерінің схемалары толығымен дәл келеді. Атомдар бір-біріне жақындаған сайын, олардың арасындағы өзара әсерлесулер күшейе түседі де, деңгейлердің жағдайын өзгертуге әкеліп соғады. Деңгейлері бірдей N атомдардың орнына, бір-біріне өте жақын, бірақ дәл келмейтін N деңгейлер пайда болады. Сонымен, кристалдағы жекеленген атомның әрбір деңгейі N жиі орналасқан деңгейлерге жіктеледі, соның нәтижесінде жолақ немесе зона түзіледі.
Әр түрлі деңгей үшін жіктелу шамасы бірдей болмайды. Атомдардың сыртқы электрондармен толған деңгейлерінде ауытқуы күшті байқалады. Ішкі электрондармен толған деңгейлерде ауытқулар шамалы болады. 1. 2-суретінде деңгейлердің жіктелуі атомдардың ара қашықтығы r-дің функциясы түрінде көрсетілген. Бұл схемадан кристалдың ішкі электрондармен толған деңгейлерінің жіктелуі аз екендігі көрініп тұр. Тек валенттік электрондармен толған деңгейлердің жіктелулері ғана анық байқалады. Мұндай жіктелулерге атомның негізгі күйінде электрондар орналаспаған жоғары деңгейлері де ұшырайды. Кристалдағы көрші атомдардың арасындағы тепе-теңдік қашықтықтарының атомдардың нақты қасиеттерінен тәуелділігіне r 1 түріне, не r 2 түріне байланысты болуы мүмкін. Атомның көрші деңгейлерінен пайда болған, рұқсат етілген r 1 түріндегі зоналардың аралығында, тыйым салынған (рұқсат етілмеген) зоналар болады. Суреттегі г 2 түріндегі қашықтықта зоналардың бірін-бірі жабуы байқалады. Мұндай араласып кеткен зоналардың деңгейлерінің саны, атомның екі деңгейінің жіктелгеніндегі деңгейлердің санының қосындысына тең болады. [2] .
Энергия деңгейлерінің зоналық құрылымы периодты күйі өрісінде қозғалатын электрон үшін тікелей Шредингер теңдеуінің шешуінен алынады. Бұл өріс кристалдық тор арқылы жасалады. Тордың өрісін ескеретін Шредингер теңдеуінің түрі мынадай болады
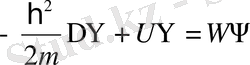
мұндағы U -функциясының мынандай қасиеттері бар:
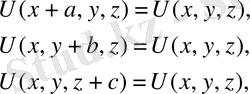
(а, в, c- х, y, z өстері бойындағы тордың периодтары) . Блохтың дәлелдеуі бойынша, потенциалы периодты болатын Шредингер теңдеуінің шешуін мына түрде жазады
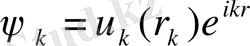 , (1. 1)
, (1. 1)
мұндағы
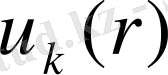 - потенциалының периодтылығы бар функция, яғни тордың периодтылығының функциясы. (1. 1) теңдеуінің шешулерін Блохтың функциялары деп атайды.
- потенциалының периодтылығы бар функция, яғни тордың периодтылығының функциясы. (1. 1) теңдеуінің шешулерін Блохтың функциялары деп атайды.
1. 3-сурет 1. 4 -сурет
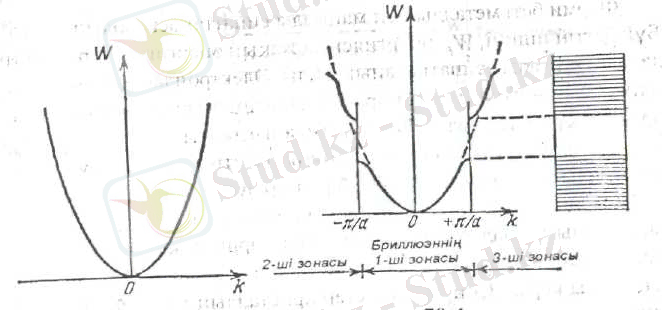
Еркін электрондарға жақындаған сайын электронның энергиясының толқындық санынан (толқындық вектор модулінен) тәуелділігі 1. 3-суретінде көрсетілген графикпен суреттеледі. Энергияның мәндері бір ізді квазиүздіксіз болады. Демек,
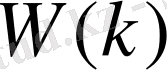 - нің графигі дискретті нүктелерден тұрады. Алайда, бұл нүктелер өте жиі орналасқандықтан, біз ол нүктелерге қарағанда, тұтас қисыққа ұласқанын көреміз.
- нің графигі дискретті нүктелерден тұрады. Алайда, бұл нүктелер өте жиі орналасқандықтан, біз ол нүктелерге қарағанда, тұтас қисыққа ұласқанын көреміз.
Өріс периодты болған жағдайда, W - нің k - дан тәуелділігі 1. 4-суретіндегідей болады. Суретке қарағанда, тұтас сызықтармен кескінделген квазиүздіксіз өзгеретін энергияның зоналары (рұқсат етілген зоналар) тыйым салынған зоналармен алмасып отыратындығы көрінеді. Әрбір рұқсат етілген зона жақын орналасқан дискретті деңгейлерден тұрады. Олардың саны кристалл үлгідегі атомдар санына тең.
Қарастырылатын k - кеңістік аймағының ішінде, кристалдың электрондарының энергиясының квазиүздіксіз өзгеруін, Бриллюэна зонасы дейді. Зона шекараларында энергия үзіліске ұшырайды. 1. 4-суреті бір өлшемді кристалл болған жағдайдағы Бриллюэн зоналарын бейнелейді. Үш өлшемді кристалдар үшін Бриллюэн зоналарының шекаралары тұйық, көп қырлы бет болады. Олар бірінің ішіне бірі қамалады. W -нің тиісті мәні
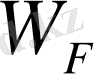 -ке тең болғанда,
-ке тең болғанда,
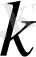 -кеңістіктегі (немесе р - кеңістіктегі) изоэлектрондық бетті Ферми деңгейі деп атағанымызды еске салайық. Еркін элекрондар жағдайында бұл бет сфера түрінде болады. Металдың өткізгіштігінің электрондары үшін бетінің пішіні кристалдық тордың қасиетінен тәуелді және түрі күрделі, кейде таңқаларлық болады. Бірқатар металдар үшін Ферми деңгейінің пішіні тәжірибе жүзінде өте үлкен дәлдікпен анықталады. [3]
-кеңістіктегі (немесе р - кеңістіктегі) изоэлектрондық бетті Ферми деңгейі деп атағанымызды еске салайық. Еркін элекрондар жағдайында бұл бет сфера түрінде болады. Металдың өткізгіштігінің электрондары үшін бетінің пішіні кристалдық тордың қасиетінен тәуелді және түрі күрделі, кейде таңқаларлық болады. Бірқатар металдар үшін Ферми деңгейінің пішіні тәжірибе жүзінде өте үлкен дәлдікпен анықталады. [3]
Ферми деңгейі металдың ең маңызды сипаттамасы болып табылады. Бұл беттің пішіні,
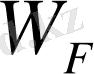 энергиясына жақын энергиясы бар, электрондардың қозғалыс сипатын анықтайды. Электрондардың қозғалыс сипаты, осыған ұқсас магнит өрісінің металға әсері кезінде байқалатын, әр түрлі құбылыстардың физикасын анықтайды.
энергиясына жақын энергиясы бар, электрондардың қозғалыс сипатын анықтайды. Электрондардың қозғалыс сипаты, осыған ұқсас магнит өрісінің металға әсері кезінде байқалатын, әр түрлі құбылыстардың физикасын анықтайды.
Сонымен, кристалдағы валенттік электрондардың мүмкін деген энергиялық мәндерінің спектрі бірқатар рұқсат етілген және тыйым салынған зоналарға жіктеледі. Демек, кристалда атом неғұрлым көп болса, соғұрлым зоналардағы деңгейлер бір-біріне жақын тығыз орналасады. Рұқсат етілген зонаның енінің шамасы бірнеше электровольтқа тең болуы керек. Сондықтан, егер кристалдың
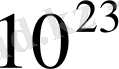 атомдары болса, онда зонадағы көрші деңгейлердің арасы шамамен ~
атомдары болса, онда зонадағы көрші деңгейлердің арасы шамамен ~
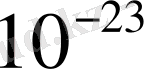 эВ-қа тең екендігі шығады.
эВ-қа тең екендігі шығады.
Әрбір энергия деңгейі k - нің белгілі мәніне жауапты. Кванттық caн
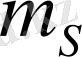 екі мән қабылдай алатын болғандықтан, кез-келген рұқсат етілген деңгейде, қарама-қарсы спиндері бар екі электрон болуы мүмкін.
екі мән қабылдай алатын болғандықтан, кез-келген рұқсат етілген деңгейде, қарама-қарсы спиндері бар екі электрон болуы мүмкін.
Энергиялық зоналар тұрғысынан алғанда металдардың, жартылай өткізгіштердің және диэлектриктердің бар болуы туралы бірдей көзқараспен түсіндіруге болады.
Атомның, негізгі күйінде валенттік электрондары орналасқан деңгейден пайда болған рұқсат етілген зонаны, біз валенттік зона деп атаймыз. Абсолют нөлде валенттік электрондар қос-қостан төменгі деңгейдің валенттік зоналарын толтырады. Одан жоғары рұқсат етілген зоналар электрондармен толмаған, бос болады. 1. 5-суретінде валенттік зоналардың электрондар толу дәрежесінің және тыйым салынған зонаның енінің үш мүмкін деген жағдайының тәуелділігі келтірілген. 1. 5, а-суретінде электрондармен валенттік зона толығымен толтырылмаған. Сондықтан да жоғары деңгейдегі электрондарға өте аз ғана энергия берсе
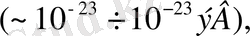 онда олар одан да жоғары деңгейге оңай көше алады. Жылулық қозғалыстың
kT
энергиясы 1
К
-де
онда олар одан да жоғары деңгейге оңай көше алады. Жылулық қозғалыстың
kT
энергиясы 1
К
-де
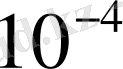 эВ шамасындай болады. Демек, абсолют нөлден айрықша температурада, электрондардың, біршама бөлігі жоғарғы деңгейге көшеді. Сөйтсек, электр өрісінің электронға әсерінен пайда болған энергияда да, электрондарды жоғары деңгейге көшіруге жеткілікті болады екен. Сондықтан электрондар электр өрісінде үдетіледі және өрістің бағытына қарсы бағытта қосымша жылдамдық алады. Міне, осындай схемалы энергиялық денгейлі кристалл металдарға жатады.
эВ шамасындай болады. Демек, абсолют нөлден айрықша температурада, электрондардың, біршама бөлігі жоғарғы деңгейге көшеді. Сөйтсек, электр өрісінің электронға әсерінен пайда болған энергияда да, электрондарды жоғары деңгейге көшіруге жеткілікті болады екен. Сондықтан электрондар электр өрісінде үдетіледі және өрістің бағытына қарсы бағытта қосымша жылдамдық алады. Міне, осындай схемалы энергиялық денгейлі кристалл металдарға жатады.
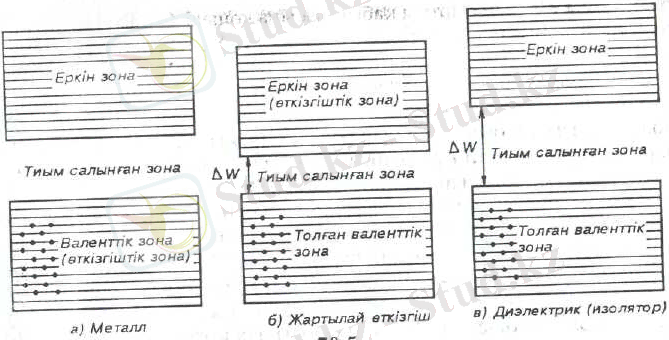
1. 5- сурет.
1. 5-суретінің б және в жағдайларында валенттік зонаның деңгейлерінің бәрі электрондармен толған. Электрондардың энергиясын көбейту үшін оған қосымша берілетін энергияның шамасы тыйым салынған зонаның ені
 -ден кіші болмауы керек. Электр өрісінің (мынадай кернеулік жағдайында кристалды электрлік тесіп өту болмайды) электронға мұндай энергия беруге ешқандай мүмкіндігі жоқ. Бұл шарт бойынша кристалдың электрлік қасиеті тыйым салынған зонаның
-ден кіші болмауы керек. Электр өрісінің (мынадай кернеулік жағдайында кристалды электрлік тесіп өту болмайды) электронға мұндай энергия беруге ешқандай мүмкіндігі жоқ. Бұл шарт бойынша кристалдың электрлік қасиеті тыйым салынған зонаның
 енімен анықталады. Егер оның ені онша үлкен болмаса (бірнеше ондаған электрон вольт шамасында), онда жылулық қозғалыстың энергиясы электрондардың белгілі бір бөлігін жоғарғы деңгейге көшіруге шамасы келеді. Бұл электрондардың жағдайы металдағы валенттік электрондардың жағдайына ұқсас. Еркіндік зонасы енді олар үшін өткізгіштік зона болады. Соның нәтижесінде, валенттік электрондарға жоғарғы босаған деңгейге көшуге мүмкіндік туады. Мұндай затты электрондық жартылай өткізгіш деп атайды. [4] .
енімен анықталады. Егер оның ені онша үлкен болмаса (бірнеше ондаған электрон вольт шамасында), онда жылулық қозғалыстың энергиясы электрондардың белгілі бір бөлігін жоғарғы деңгейге көшіруге шамасы келеді. Бұл электрондардың жағдайы металдағы валенттік электрондардың жағдайына ұқсас. Еркіндік зонасы енді олар үшін өткізгіштік зона болады. Соның нәтижесінде, валенттік электрондарға жоғарғы босаған деңгейге көшуге мүмкіндік туады. Мұндай затты электрондық жартылай өткізгіш деп атайды. [4] .
Тыйым салынған зонаның ені
 үлкен (реті бірнеше электрон вольт) болса, онда жылулық қоғалыс байқалған мөлшердегі электрондарды бос зонаға көшіре алмайды. Бұл жағдайда кристалды диэлектриктер деп атайды. Осындай денелердің мысалы ретінде ас тұзы
NaCl
-ды алуға болады.
NaCl
молекуласындағы
Na
-дің сыртқы (валенттік) электроны
Сl
-дың сыртқы қабықшасына көшеді. Соның нәтижесінде, электрон қабықшасына толық орныққан
үлкен (реті бірнеше электрон вольт) болса, онда жылулық қоғалыс байқалған мөлшердегі электрондарды бос зонаға көшіре алмайды. Бұл жағдайда кристалды диэлектриктер деп атайды. Осындай денелердің мысалы ретінде ас тұзы
NaCl
-ды алуға болады.
NaCl
молекуласындағы
Na
-дің сыртқы (валенттік) электроны
Сl
-дың сыртқы қабықшасына көшеді. Соның нәтижесінде, электрон қабықшасына толық орныққан
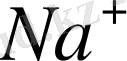 және
және
 иондары түзіледі. Демек,
NaCl
кристалындағы натрий ионының өткізгіштік зонасынан жоғары жатқан хлордың валенттік зонасының орналасуы, яғни
иондары түзіледі. Демек,
NaCl
кристалындағы натрий ионының өткізгіштік зонасынан жоғары жатқан хлордың валенттік зонасының орналасуы, яғни
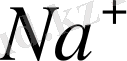 және
және
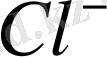 зоналарының орналасу аралықтары 6 эВ-қа тең болатындығын көрсетеді. Олай болса, сыртқы электр өрісі электрондармен толық толған
зоналарының орналасу аралықтары 6 эВ-қа тең болатындығын көрсетеді. Олай болса, сыртқы электр өрісі электрондармен толық толған
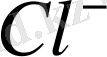 -дың, зонасындағы электрондарды
-дың, зонасындағы электрондарды
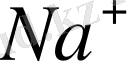 - дің өткізгіштік бос зонасына көшіре алмайды. [5] .
- дің өткізгіштік бос зонасына көшіре алмайды. [5] .
1. 2. ЖАРТЫЛАЙ ӨТКІЗГІШТЕР
Жартылай өткізгіштер деп валенттік зоналары электрондармен толығымен толған тыйым салынған зонасының ені үлкен емес (жартылай өткізгіштің өзінікі 1 эВ) кристалдық заттарды айтады (1. 5, б-суретті қараңыз) . Жартылай өткізгіштің өзінің аталуынан көрініп тұрғандай, ол металл мен диэлектриктің аралығында жатады. Алайда, оның сипаты өткізгіштігінің өте жоғарылығында емес, мәселе қайта температура өскен сайын өткізгіштігінің өсетіндігінде болып табылады (бұл жерде айта кететін жағдай, металдарда өткізгіштік өсудің орнына төмендейді) .
Жартылай өткізгіштер меншікті және қоспалы өткізгіштер деп бөлінеді. Ішінде қоспасы жоқ жартылай өткізгіштіктің өткізгіштігін меншікті өткізгіштігі деп атайды. Меншікті өткізгіштерге химиялық таза жартылай өткізгіштер жатады. Қоспалы жартылай өткізгіштердің электрлік қасиеттері оларға жасанды түрде ендірілген қоспалардың қасиеттеріне байланысты болады.
Жартылай өткізгіштердің қасиеттерін қарастырғанда "кемтік" /саңылау/ деген ұғымның ролі үлкен болады. Сондықтан осы ұғымның физикалық мазмұнына тоқталайық.
Абсолют нөл температурада жартылай өткізгіштердің меншікті өткізгіштігі жоқ, олар электрді өткізбейді. Оның себебі валенттік зонадағы барлық деңгейлер электрондармен толып болған, өткізгіштік зонада электрондар жоқ (1. 6, а-сурет) . Электр өрісі электрондарды валенттік зонадан өткізгіштік зонаға көшіре алмайды.
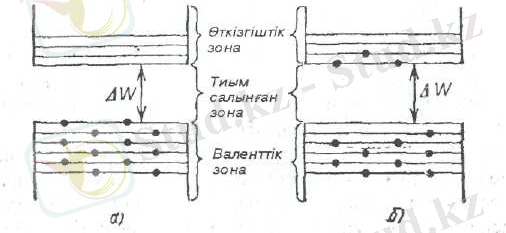 1. 6-сурет
1. 6-сурет
Сондықтан да, меншікті жартылай өткізгіштер абсолют нөл температурада өздерін диэлектриктер тәрізді ұстайды. 0 0 К температурадан өзгеше температурада, жылулық қозудың нәтижесінде, валенттік зонаның жоғары деңгейлерінен электрондардың бір бөлігі өткізгіштік зонаның төменгі деңгейлеріне өтеді (1. 6, б-сурет) . Бұл жағдайда электр өрісі өткізгіштік зонада тұрған электрондардың күйін өзгертуге мүмкіндік алады. Coнымен қатар, валенттік зонада бос (ваканттық) деңгейлердің пайда болуы сыртқы өрісінің әсеріне байланысты осы зонаның электрондары өздерінің жылдамдықтарын өзгертуі мүмкін. Соның нәтижесінде, жартылай өткізгіштің электр өткізгіштігі нөлден өзгеше болады. [6] .
Байқасақ, бос деңгейдің болуы кезінде, валенттік зонаның электрондары "кемтік" деп аталатын оң зарядталған квази бөлшектердің қозғалғаны тәрізді мінез көрсетеді екен. Валенттік зонаның толығымен толуына байланысты өткізгіштіктің нөлге тең болуынан, осындай зонаның барлық электрондарының жылдамдықтарының қосындысы нөлге тең болатындығы келіп шығады:
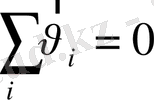
Бұл қосындыдан k -шы электронның жылдамдығын бөліп қараймыз:
 Осыдан
Осыдан
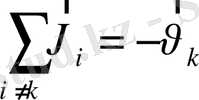
Бұл алынған қатынастан, егер к -шы электрон валенттік зонада жоқ болса, онда қалған электрондардың жылдамдықтарының қосындысы
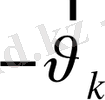 ға тең болатындығы келіп шығады. Демек, осы электрондардың бәрі (-е) (
ға тең болатындығы келіп шығады. Демек, осы электрондардың бәрі (-е) (
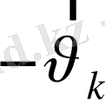 ) = е
) = е
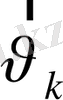 тоқты тудырады. Сонымен бұдан байқайтынымыз, пайда болған ток заряды + е, жылдамдығы, жоқ электронның жылдамдығындай болатын, бөлшектің тудырған электр тоғына эквивалент болады екен. Бұл ойдан шығарылған бөлшек " кемтік " бөлып табылады.
тоқты тудырады. Сонымен бұдан байқайтынымыз, пайда болған ток заряды + е, жылдамдығы, жоқ электронның жылдамдығындай болатын, бөлшектің тудырған электр тоғына эквивалент болады екен. Бұл ойдан шығарылған бөлшек " кемтік " бөлып табылады.
Кемтік ұғымына біз мынадай жолмен келеміз. Валенттік зонаның төбесінде бос деңгейлер пайда болады. Энергиялық зонаның төбесіндегі электронның тиімділік, (эффективтік) массасы теріс болуы керек. Заряды (-е) және m* теріс массалы бөлшектің болмауы, оған эквиваленті оң зарядталған заряды (+е) және m* оң массалы болатын бөлшектің, яғни кемтіктің болуына әкеледі.
Кристалдағы зарядты тасымалдаушы (электрондарға) сыртқы электр өрісінен басқа кристалдың ішкі электр өрісіне периодты түрде әсер етіп тұрады. Кристалдың өрісінің әсері электронның тиімділік (эффективтік) массасы (m*) туралы түсінікті енгізу арқылы есепке алады. Бұл массаны енгізгенде кристалдың ішкі өрісінің электронға әсері есепке алынатындай болуы ескеріледі және m* тиімділік (эффективтік) массалы электрон тек қана сыртқы өрістің әсері арқылы қозғалады деп есептелінеді.
Электронның тиімділік массасын түсіну үшін механикадағы ұқсастықты пайдаланамыз. Ыдысқа құйылған тығыздық
 сұйықта.
сұйықта.
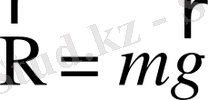 ауырлық күшінің әсерімен тығыздығы
ауырлық күшінің әсерімен тығыздығы
 болатын шарик қозғалысын
болатын шарик қозғалысын
 (1. 7-сурет) .
(1. 7-сурет) .
(1. 7-сурет) . Шарикке ауырлық күшінен басқа, "ішкі" күштің рөлін атқаратын архимед күші әсер етеді. Сондықтан Ньютонның 2-ші заңы бойынша

Осыдан қозғалыс тек тиімділіктік масса
 қатысатын ауырлық күшінің әсерінен жүреді деп қарасақ, мына өрнекті жазамыз
қатысатын ауырлық күшінің әсерінен жүреді деп қарасақ, мына өрнекті жазамыз
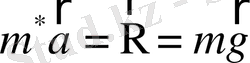 мұндағы
мұндағы
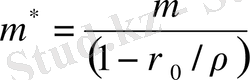
Бұдан
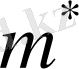 тиімділіктік массаның оң не теріс болуы
тиімділіктік массаның оң не теріс болуы
 және
және
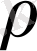 қатынасынан тәуелді болады.
қатынасынан тәуелді болады.
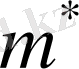 = const жағдайын қарастырамыз:
= const жағдайын қарастырамыз:
1) егер электрон өткізгіштік зонаның "түбінде" болса, онда
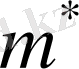 > 0 оң; 2) егер электрон валенттік зонаның "төбесінде" болса, онда
> 0 оң; 2) егер электрон валенттік зонаның "төбесінде" болса, онда
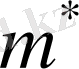 < 0 теріс.
< 0 теріс.
Сонымен, кемтікті оң зарядты және оң тиімділіктік массалы нақты бөлшек деп санаған жөн және кемтіктік өткізгіштіктігіне байланысты барлық мәселелерді электрондық өткізгіштікке ұқсас деп білу керек. [7] .
1. 3. ЖАРТЫЛАЙ ӨТКІЗГІШТЕРДІҢ МЕНШІКТІ ӨТКІЗГІШТІГІ
Меншікті өткізгіштік электрондардың валенттік зонаның жоғарғы деңгейімен өткізгіштік зонаға көшуінен пайда болады. Бұл кезде өткізгіштік зонада токты тасымалдаушы бірқатар бөлшектер электрондар саны пайда болады. Электрондар зонаның түбіне жақын орналасады. Соның нәтижесінде, бір мезгілде жоғарғы деңгейдегі валенттік зонада соншалықты орын босайды да, кемтіктер пайда болады.
Электрондардың валенттік зона және өткізгішік зона деңгейлерінде таралулары Ферми-Дирак функциясымен сипатталады. Бұл таралуларды энергиялық зоналар схемасын таралу функциясымен біріктіру арқылы, 1. 8-суретіндегідей көрнекі етіп, бейнелеуге болады.
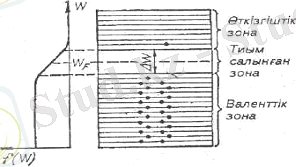 1. 8-сурет
1. 8-сурет
Тиісті есептеулерге қарағанда, валенттік зонаның төбесінен бастап санаған меншікті жартылай өткізгіштің Ферми деңгейінің мәні мынадай болады

мұндағы
 -тыйым салынған зонаның ені, ал
-тыйым салынған зонаның ені, ал
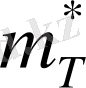 және
және
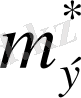 -өткізгіштік зонадағы тесік пен электронның тиімділігі массалары. Көбінесе екінші қосылғыш ескерусіз қалдыратын аз шама болғандықтан, W
F
= ∆W/2 деп жазамыз. Бұл Ферми деңгейінің тыйым салынған зонаның ортасында жатқандығын көрсетеді (1. 8 - суретті қараңыз) . Демек, өткізгіштік зонаға көшкен электрондар үшін, W-WF шамасының тыйым салынған зонаның енінен айырмашылығы аз болады. Өткізгіштік зонаның деңгейі таралу қисығының соңында орналасады. Сондықтан, олардың электрондармен толтырылу ықтималдылығын (7. 11) өрнегі бойынша анықтауға болады. Осы өрнекке W - WF ≈= ∆W/2 -ні қойып, мынаны аламыз
-өткізгіштік зонадағы тесік пен электронның тиімділігі массалары. Көбінесе екінші қосылғыш ескерусіз қалдыратын аз шама болғандықтан, W
F
= ∆W/2 деп жазамыз. Бұл Ферми деңгейінің тыйым салынған зонаның ортасында жатқандығын көрсетеді (1. 8 - суретті қараңыз) . Демек, өткізгіштік зонаға көшкен электрондар үшін, W-WF шамасының тыйым салынған зонаның енінен айырмашылығы аз болады. Өткізгіштік зонаның деңгейі таралу қисығының соңында орналасады. Сондықтан, олардың электрондармен толтырылу ықтималдылығын (7. 11) өрнегі бойынша анықтауға болады. Осы өрнекке W - WF ≈= ∆W/2 -ні қойып, мынаны аламыз
 (1. 2)
(1. 2)
Өткізгіштік зонаға өткен электрондар саны демек, нәтижесінде пайда болған кемтіктердің саны (1. 2) ықтималдығына пропорционал болады. Бұл электрондар мен кемтіктер тоқты тасымалдаушы болып саналады. Өткізгіштік тасымалдау санына пропорционал болғандықтан, ол (1. 2) өрнегіне де пропорционал. Демек, меншікті жартылай өткізгіштердің электр өткізгіштігі температура өскен сайын тез өсіп, мынадай заңдылықпен өзгереді. [8] .
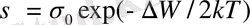 (1. 3)
(1. 3)
мұндағы
 -тыйым салынған зонаның ені, ал
-тыйым салынған зонаның ені, ал
 -экспонентке қарағанда, температурамен өзгерісі өте баяу жүретін шама. Сондықтан оны бірінші жуықтауда константа деп есептеуге болады.
-экспонентке қарағанда, температурамен өзгерісі өте баяу жүретін шама. Сондықтан оны бірінші жуықтауда константа деп есептеуге болады.
Егер 1. 3-сурегіндегі графикке In
 -ның 1/Т дан тәуелділігін салса, онда графикте меншікті жартылай өткізгіштер үшін түзу сызық алынады. Осы түзудің көлбеулігінен тыйым салынған зонаның
-ның 1/Т дан тәуелділігін салса, онда графикте меншікті жартылай өткізгіштер үшін түзу сызық алынады. Осы түзудің көлбеулігінен тыйым салынған зонаның
 енін анықтауға болады. Әдетте, жартылай өткізгіштер қатарына Менделеев периодтық жүйенің IV тобындағы германий және кремний элементтері жатады. Олардың әрбір атомы одан бірдей қашықтықта тұрған көрші төрт атомдармен ковалентті (қос электрондармен) байланысқан, алмаз түріндегі торды құрайды.
енін анықтауға болады. Әдетте, жартылай өткізгіштер қатарына Менделеев периодтық жүйенің IV тобындағы германий және кремний элементтері жатады. Олардың әрбір атомы одан бірдей қашықтықта тұрған көрші төрт атомдармен ковалентті (қос электрондармен) байланысқан, алмаз түріндегі торды құрайды.
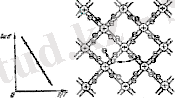
1. 9-сурет 1. 10-сурет
Шартты түрде атомдардың өзара орналасуларын жазық құрылым түрінде 1. 10-суретіндегідей тәрізді көрсетуге болады. Суреттегі " + " таңбасы бар дөңгелекшелер оң зарядталған атом қалдықтары (валенттік электрондарыман айрылған атомдардың бөлігі), "-" таңбасы бар дөңгелекшелер валенттік электрондар, қос сызықтар коваленттік байланыстарды көрсетеді.
Жеткілікті шамадағы жоғары температурада жүретін жылулық қозғалыстар қос электрондардың бірінің байланысын үзіп, бір электронды босатып жіберуі мүмкін. Электрон ұшып шыққаннан кейін, қалған орын енді бейтарап болудан калады, оның орнын артық +е оң заряд басады, яғни кемтік пайда болады (1. 10-суретінде ол пунктир дөңгелекше түрінде көрсетілген) . Осы орынға көрші тұған қос электронның бірі ұшып келіп, орналасуы мүмкін. Соның нәтижесінде, ендігі жерде кристалда пайда болған кемтікте босанып шыққан электрон секілді көшіп жүреді.
Еркін электрон мен кездескен кемтік жағдайда, олар рекомбинацияланады (бірігеді) . Бұл электронның кемтіктің айналасындағы артық oң зарядты бейтараптауы деген сөз. Сөйтіп, электрон енді еркін қозғалмайтын жағдайға көшеді. Ол қайтадан босанып шығу үшін кристалдық тордан жеткілікті мөлшерде энергия алуы керек. Рекомбинация процесі бір мезгілде электронның да, кемтіктің де жоғалып кетуіне әкеліп соғады. 1. 8-суретіндегі схемада рекомбинация процесінде, электронмен өткізгіштің зонадан валенттік зонаның бос деңгейіне көшу процесі бейнеленген.
Сонымен меншікті жартылай өткізгіштерде бір мезгілде екі процесс: электрондар және кемтіктердің қатар пайда болуы және рекомбинация, яғни электрондар және кемтіктердің қатар жоғалып кетуі жүреді. Бірінші процестің ықтималдылығы температура өскен сайын арта түседі. [9] .
Рекомбинация ықтималдылығы еркін электрондардың санына да, кемтіктердің санына да пропорционал. Демек, әрбір температураға тиісті белгілі бір электрондар мен кемтіктердің тепе-теңдік концентрациясы сәйкес келеді және ол температура мен (1. 2) өрнегіне пропорционал өзгереді.
Сыртқы электр өрісі жоқ жағдайда өткізгіштік электрондары мен кемтіктер хаосты түрде қозғалады. 1. 11-суретіндегідей жартылай өткізгішті сыртқы кернеу көзіне қосқанда, ол жартылай өткізгіштің ішінде Е
 1. 11-сурет
1. 11-сурет
электр өрісін тудырады. Өткізгіш электрондар өрістің күш сызықтарына қарсы қозғалады, ал кемтіктер (оң заряд сияқты) қарама-қарсы жаққа орын ауыстырады. Мұның мәнісі меншікті электр өткізгіштік екі таңбалы зарядтар теріс электрондар және оң кемтіктердің тасымалдануы арқылы жүреді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz