Шектелген облыста берілген толқындық оператордың шешімдерін зерттеу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:
«Шектелген облыста берілген толқындық оператордың шешімі туралы» тақырыбына жазылған М - 28 - 1 тобының білімгері Рысбаева Динараның дипломдық жұмысына
АННОТАЦИЯ
Бұл дипломдық жұмыста шектелген облыста берілген біртекті емес толқындық оператордың шешімін табу мақсатында екінші ретті дербес туындылы дифференциал теңдеудің классификациясының маңызы, Даламбер формуласы және оның мысалдары, толқындық теңдеудің тарихы, сондай-ақ біртекті және біртекті емес толқындық теңдеулері және айнымалыны ажырату немесе Фурье әдістеріне талдау жүргізілген.
Дипломдық жұмыс 3 бөлімнен, 7 сызбадан және 50 беттен тұрады.
АННОТАЦИЯ
На дипломную работу студента группы М - 28 - 1 Рысбаевой Динары на тему «Оценка и его совершенствовать систем управления формирование рынка труда в регионе» (на примере данных отдела «Трудоустроиства и социальных программ» акимата Т. Рыскуловского района Жамбылской области)
В данной дипломной работе рассмотрено научный-теоретичная сущность в период рыночных отнашений в регионе рынка труда и управления значения и спрос, предложения и особенности равенства рынке труда, а также проведен анализ выполнения плана структуры местного рынка и основной социально-экономическое состояние в регионе покозателей динамики. На основе проведенного анализа предложены совершенствовать механизмы управления от государства в регионе рынка труда и снижать уровня безработицы повысить рациональность местных жителей с помощью экспертного метода.
Дипломная работа состоит из 3 разделов, 7 графиков и 50 страниц.
Мазмұны
Кіріспе . . .
І. Теориялық бөлім . . .
1. 1 Сызықты кеңістік . . .
1. 2 Метрикалық кеңістік . . .
1. 3 Нормаланған кеңістік . . .
1. 4 Гильберт кеңістігі . . .
1. 5 Сызықты оператор . . .
1. 6 Түйіндес оператор . . .
ІІ. Гиперболалық түрдегі теңдеулер . . .
2. 1 Екінші ретті дербес туындылы дифференциал теңдеудің
классификациясы . . .
2. 2 Даламбер формуласы және оның мысалдары . . .
2. 3 Толқындық теңдеудің тарихы . . .
2. 4 Біртекті және біртекті емес толқындық теңдеулер . . .
2. 5 Фурье түрлендіруі және айналу формуласы
2. 6 Айнымалыны ажырату әдісі немесе Фурье әдісі . . .
ІІІ. Шектелген облыста берілген толқындық оператордың шешімі
туралы . . .
ІV. Қорытынды . . .
V. Пайдаланылған әдебиеттер тізімі . . .
Кіріспе
Дипломдық жұмысымның тақырыбы «Шектелген облыста берілген толқындық оператордың шешімі туралы». Дипломдық жұмыс математикалық физика теңдеулері және функционалдық анализ пәні бойынша жазылған. Шектелген облыста берілген толқындық оператордың шешімін табу тақырыптың өзектілігі болып табылады. Бұл дипломдық жұмыстың негізгі мақсаты шектелген облыста толқындық теңдеуді шешімін таба отырып, теоремаға келу. Сонымен қатар біртекті емес теңдеуді біртекті теңдеу арқылы шешу жолдарын зерттеу болып табылады.
Дипломдық жұмысым үш бөлімнен тұрады. Кіріспе, бірінші бөлім - теориялық бөлім. Бөлім функционалдық анализ пәніне байланысты керекті анықтамалар мен теоремалар жазылған. Олар: сызықты кеңістік, метрикалық кеңістік, нормаланған кеңістік, гильберт кеңістігі, сызықты оператор, түйіндес оператор. Екінші бөлімнің тақырбы гиперболалық түрдегі теңдеулер. Бұл бөлім алты тақырыпшадан тұрады: екінші ретті дербес туындылы дифференциал теңдеудің классификациясы, Даламбер формуласы және оның мысалдары, толқындық теңдеудің тарихы, біртекті және біртекті емес толқындық теңдеулер, Фурье түрлендіруі және айналу формуласы, айнымалыны ажырату әдісі немесе Фурье әдісі. Бұл бөлімде мен жұмысымды толықтай ашу үшін қажетті мағлұматтарды жаздым. Ал үшінші бөлімнің тақырыбы шектелген облыста берілген толқындық оператордың шешімі туралы, яғни қорытынды бөлім. Осы бөлімдерді зерттей отырып, қорытынды жасадым. Және де тақырыпты ашу үшін қолданылған әдебиеттер тізімін жаздым.
Даламбер операторы (толқындық оператор) - екінші ретті дифференциалдық оператор
Ол Ж. Д’аламбер атымен аталған (J. D’Alembert, 1747) . Даламбер бірөлшемді толқындық теңдеу үшін оның қарапайым түрін қарастырған.
Электродинамикада, акустикада және толқынның таралуының басқа да есептерінде пайдаланылады. Даламбер операторы кез келген өлшемді толқындық теңдеуде шығады, және оның негізін құра отырып, тағы сол сияқты Клейна - Гордона - Фока теңдеуі де шығады.
Математикада толқындық теңдеу - дербес туындылы сызықты гиперболалық дифференциалдық теңдеу.
Екінші ретті дербес туындылы гиперболалық түрдегі теңдеу тербелістің процесстерімен байланысты физикалық есептерде жиі кездеседі. Қарапайым гиперболалық түрдегі теңдеуді струнның тербеліс теңдеуі деп атайды.
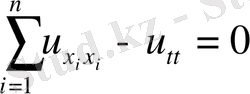 (1)
(1)
теңдеудің шешімі толқын деп, ал (1) теңдеудің өзі толқындық деп аталады.
(1) теңдеуге сәйкес келетін
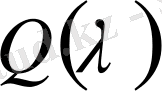 сипаттамалық формасы мынадай түрде болғандықтан
сипаттамалық формасы мынадай түрде болғандықтан
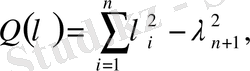
ол гиперболалық түрдегі теңдеу болып табылады.
І - бөлім. Теориялық бөлім
1. 1. Сызықты кеңістік
Сызықты кеңістіктің түсінігі қазіргі математиканың маңызды түсінігінің бірі болып табылады. Жазықтықта немесе үш өлшемді кеңістікте барлық вектордың жиынтығы, әртүрлі функциялар жиындарында (функционалдық кеңістік) сызықтылықтың тек сол бір жалпы қасиетін сипаттауға болатыны өте маңызды. Математикада қабылданған аксиоматикалық қадаммен, сызықты кеңістіктің жалпы түсінігін анықтайтын, аксиома жүйесінде осы қасиеттен негізгілері ерекшеленеді.
А н ы қ т а м а.
Егер келесі екі операция анықталса, онда Е жиынының
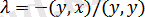 элементтері
сызықты кеңістік
деп аталады.
элементтері
сызықты кеңістік
деп аталады.
1. Қосынды деп аталатын,
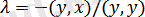 анықталған элементі әрбір
анықталған элементі әрбір
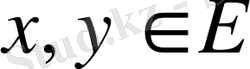 екі элементке сәйкесінше қойылған.
екі элементке сәйкесінше қойылған.
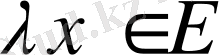 анықталған элементке -
анықталған элементке -
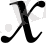 элементін
элементін
 скалярынакөбейтіндісі кез келген
скалярынакөбейтіндісі кез келген
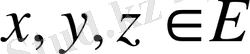 және кез келген
және кез келген
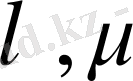 үшін келесі қасиеттер орындалатын әрбір
үшін келесі қасиеттер орындалатын әрбір
 элементіне және әрбір
элементіне және әрбір
 (скалярға) санға сәйкесінше қойылған:
(скалярға) санға сәйкесінше қойылған:
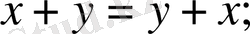
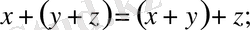
 болатындай,
болатындай,
 элементі бар болады;
элементі бар болады;
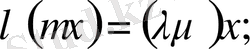
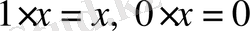 (сол жағында 0 - скаляр, ал оң жағында Ежиынының элементі) ;
(сол жағында 0 - скаляр, ал оң жағында Ежиынының элементі) ;
6)
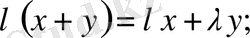
7)
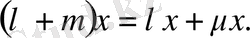
Сызықты кеңістікте
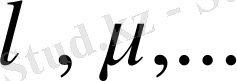 сандық (скаляр) көбейткіш ретінде нақты немесе комплекстік сандар алынады. Бірінші жағдайда Е нақты сызықты кеңістік деп аталады, ал екіншіде - комплексті сызықты кеңістік деп аталады. Барлық
сандық (скаляр) көбейткіш ретінде нақты немесе комплекстік сандар алынады. Бірінші жағдайда Е нақты сызықты кеңістік деп аталады, ал екіншіде - комплексті сызықты кеңістік деп аталады. Барлық
 элементі үшін барлық Е сызықты кеңістігінде қарама-қарсы
элементі үшін барлық Е сызықты кеңістігінде қарама-қарсы
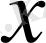 элементін анықтауға болады, бұл дегеніміз,
элементін анықтауға болады, бұл дегеніміз,
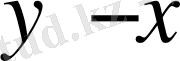 элементтерді азайту операциясы. Анықтама бойынша
элементтерді азайту операциясы. Анықтама бойынша
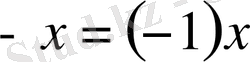 қоямыз. Сонда, 5) және 7) аксиомаға сүйеніп,
қоямыз. Сонда, 5) және 7) аксиомаға сүйеніп,
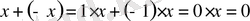
аламыз. Ары қарай
 айырымы деп мына өрнекті
айырымы деп мына өрнекті
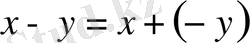
түсінетін боламыз. Енді сызықты кеңістіктің анықтамасынан шығатын, кейбір жай зерттеулер келтіреміз.
1-з е р т т е у. Нөлдік элемент жалғыз.
Д ә л е л д еу.
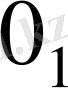 және
және
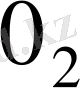 - Е-дегі нөлдер деп ұйғарамыз; сонда
- Е-дегі нөлдер деп ұйғарамыз; сонда
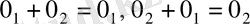 ( 3) аксиомаға сүйеніп) . Бұдан, 1) аксиома бойынша,
( 3) аксиомаға сүйеніп) . Бұдан, 1) аксиома бойынша,
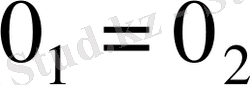 .
.
2-з е р т т е у.
Егер
 болса, мұндағы
болса, мұндағы
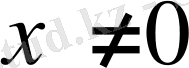 , онда
, онда

Д ә л е л д е у.
 теңдіктің екі жағында
теңдіктің екі жағында
 -ке көбейтіп,
-ке көбейтіп,
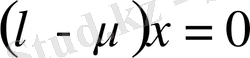 аламыз. Егер
аламыз. Егер
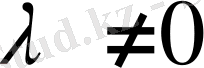 болса, онда бұдан, 4) аксиома бойынша
болса, онда бұдан, 4) аксиома бойынша
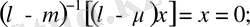 қарама-қайшылық алынды. Сондықтанда,
қарама-қайшылық алынды. Сондықтанда,

3-з е р т т е у.
Егер
 және
және
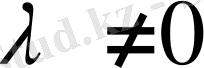 болса, мұндағы
болса, мұндағы
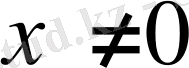 , онда
, онда

Д ә л е л д е у.
 теңдіктің екі жағында
теңдіктің екі жағында
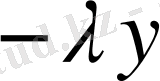 -ке көбейтіп,
-ке көбейтіп,
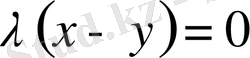 аламыз. Егер
аламыз. Егер
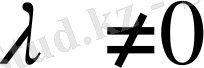 болса, онда бұдан
болса, онда бұдан
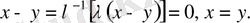
М ы с а л д а р:
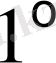 .
Барлық мүмкін векторлар жиыны (үш өлшемді кеңістікте, жазықтықта немесе түзуде) сызықты кеңістікті жасайды. Вектордың қосындысы параллелограммның ережесі бойынша анықталатынын, ал
.
Барлық мүмкін векторлар жиыны (үш өлшемді кеңістікте, жазықтықта немесе түзуде) сызықты кеңістікті жасайды. Вектордың қосындысы параллелограммның ережесі бойынша анықталатынын, ал
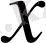 векторының
векторының
 нақты санына көбейтіндісі
нақты санына көбейтіндісі
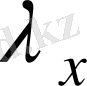 векторы арқылы анықталатынын еске түсіреміз, егер
векторы арқылы анықталатынын еске түсіреміз, егер
 және оған қарама-қарсы
және оған қарама-қарсы
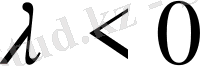 болса, оның ұзындығы
болса, оның ұзындығы
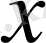 ұзындығына
ұзындығына
 көбейтіндісі, ал бағыты
көбейтіндісі, ал бағыты
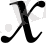 бағытына дәл келеді. Сызықты кеңістіктің аксиомалары - бұл векторлармен атақты операция қасиеттері.
бағытына дәл келеді. Сызықты кеңістіктің аксиомалары - бұл векторлармен атақты операция қасиеттері.
Осылайша, сызықты кеңістіктің элементтері міндетті түрде жалпыланған векторлар ретінде қарастырылады. «Сызықты кеңістік» терминінің орнына «векторлық кеңістік» термині де қолданылады. Ары қарай, сызықты кеңістіктің элементтерін айтқанда, біз оны вектор деп те атайтын боламыз.
 .
.
 жиынын барлық мүмкін
жиынын барлық мүмкін
 нақты сандарынан реттелген терулермен қарастырамыз.
нақты сандарынан реттелген терулермен қарастырамыз.
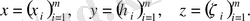
 сандарын
сандарын
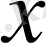 бағандарының координаталары деп атаймыз.
бағандарының координаталары деп атаймыз.
 бағандарының қосындысынан бағанды түсінетін боламыз, олардың координаталары -
бағандарының қосындысынан бағанды түсінетін боламыз, олардың координаталары -
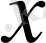 және
және
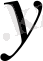 бағандарына сәйкес келетін координата, яғни
бағандарына сәйкес келетін координата, яғни
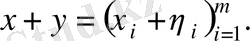
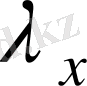 бағаннан
бағаннан
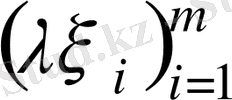 бағанын түсінетін боламыз, мұндағы
бағанын түсінетін боламыз, мұндағы
 - нақты сан. Нөлдің рөлін
- нақты сан. Нөлдің рөлін
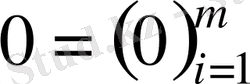 бағаны ойнайды. Бағандар операциясы координаттар операциясына, яғни сызықты кеңістік аксиомалары тривиальді орындалатын нақты сандарға келтірілетіндіктен, осы аксиомалар бағандарға да орындалады. Осылайша,
бағаны ойнайды. Бағандар операциясы координаттар операциясына, яғни сызықты кеңістік аксиомалары тривиальді орындалатын нақты сандарға келтірілетіндіктен, осы аксиомалар бағандарға да орындалады. Осылайша,
 сызықты кеңістік болып табылады.
сызықты кеңістік болып табылады.
Комплекстік сандар бағандарын комплекстік сандарға көбейтіп қарастыруға болады. Қорыта келгенде бағандардың комплексті сызықты кеңістігін аламыз.
Енді функцияның сызықты кеңістігіне мысал қарастырамыз. Алдымен кейбір жалпы ескертулер жасаймыз.
 - кез келген табиғаттың кейбір
- кез келген табиғаттың кейбір
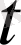 жиынының элементтері және әрбір
жиынының элементтері және әрбір
 -ға Е сызықты кеңістігінде
-ға Е сызықты кеңістігінде
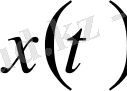 элементі сәйкес қойылған болсын, яғни
элементі сәйкес қойылған болсын, яғни
 анықталған облысында
анықталған облысында
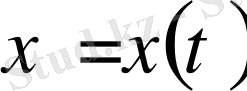 функциясы және Е-де облыстың мәндері берілген.
функциясы және Е-де облыстың мәндері берілген.
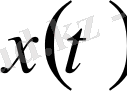 және
және
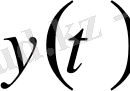 екі функцияның
екі функцияның
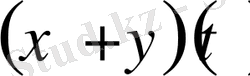 қосындысынан
қосындысынан
 функциясын түсінетін боламыз.
функциясын түсінетін боламыз.
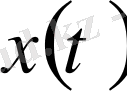 функциясын
функциясын
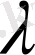 санына
санына
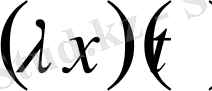 көбейтіндісінен
көбейтіндісінен
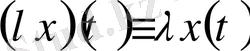 функциясын түсінетін боламыз.
функциясын түсінетін боламыз.
Төменде ұсынылған мысалдарда нақты немесе комплексті мәнді функция қарастырылған, Е - нақты ось немесе комплексті жазықтық. 2 мысалдағысияқы, осындай функциялардың операциясы нақты немесе комплексті сандар операциясына жинақталады.
 деп белгілеп және сол немесе басқа функциялар классын таңдай отырып, біз автоматты түрде сызықты кеңістіктің аксиомаларының орындалуын аламыз, егер тек
деп белгілеп және сол немесе басқа функциялар классын таңдай отырып, біз автоматты түрде сызықты кеңістіктің аксиомаларының орындалуын аламыз, егер тек
 және
және
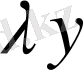 таңдалынған функциялар классына
таңдалынған функциялар классына
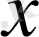 және
және
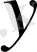 -пен бірге жататын болса.
-пен бірге жататын болса.
 . Скалярлық элементтері арқылы
. Скалярлық элементтері арқылы
 ретпен барлық тіктөртбұрышты матрицалық
ретпен барлық тіктөртбұрышты матрицалық
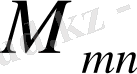 жиынын қарастырамыз.
жиынын қарастырамыз.
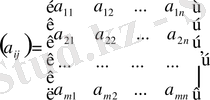
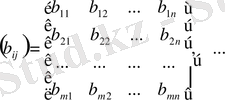
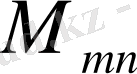 операциясын анықтаймыз
операциясын анықтаймыз
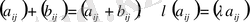
Матрицалардан алынған операция сандардан алынған операцияға жинайтын болса, онда аксиоманың дұрыстығы белгілі. Егер матрицаның және
 скалярларының элементтері нақты (комплексті) болса, онда біз нақты (комплексті) сызықты кеңістікке келеміз.
скалярларының элементтері нақты (комплексті) болса, онда біз нақты (комплексті) сызықты кеңістікке келеміз.
1. 2. Метрикалық кеңістік
А н ы қ т а м а.
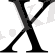 қайсыбір бос емес жиын болсын. Егер кез келген
қайсыбір бос емес жиын болсын. Егер кез келген
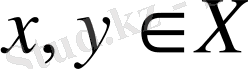 үшін нақты мәнді функция
үшін нақты мәнді функция
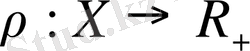 анықталып, төмендегі шарттары орындалса,
анықталып, төмендегі шарттары орындалса,
1)
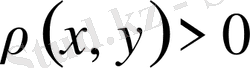 және
және
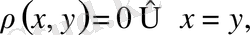
2)
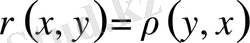 (симметриялық қасиет),
(симметриялық қасиет),
3)
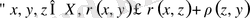 (үшбұрыш теңсіздігі)
(үшбұрыш теңсіздігі)
онда ол функцияны (шындығында функционал)
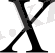 жиынындағы
метрика
немесе
ара қашықтық
функциясы
деп атайды, ал
жиынындағы
метрика
немесе
ара қашықтық
функциясы
деп атайды, ал
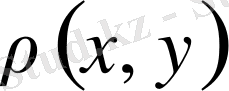 саны
саны
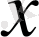 және
және
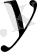 нүктелерінің арасындағы ара қашықтық.
нүктелерінің арасындағы ара қашықтық.
А н ы қ т а м а.
Бос емес
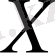 жиыны мен анықталған метрика, яғни
жиыны мен анықталған метрика, яғни
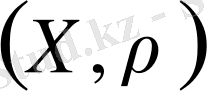 пары, метрикалық кеңістік деп аталады.
пары, метрикалық кеңістік деп аталады.
Осылайша, пар:
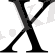 жиыны мен
жиыны мен
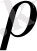 функциясы метрикалық кеңістікті жасайды; оны
функциясы метрикалық кеңістікті жасайды; оны
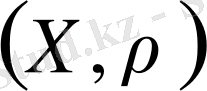 немесе
немесе
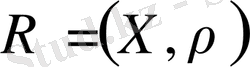
арқылы белгілейтін боламыз, немесе егер қандай метрика екендігі белгілі болса, онда жай
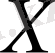 арқылы белгілейміз.
арқылы белгілейміз.
Егер 3) -ке
 қойсақ, онда 1) және 2) ескере отырып,
қойсақ, онда 1) және 2) ескере отырып,
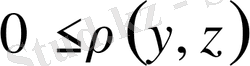 аламыз, яғни ара қашықтық функциясы - өзінің аргументтерінің теріс емес функциясы.
аламыз, яғни ара қашықтық функциясы - өзінің аргументтерінің теріс емес функциясы.
Көрсетілген үш қасиет метрикалық кеңістіктің аксиомалары деп аталынады.
Бір жиында бірнеше метрика анықтап, бірнеше метрикалық кеңістік алуға болады.
Жиі кездесетін метрикалық кеңістікке мысалдар келтіреміз.
М ы с а л д а р.
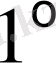 .
.
 (
(
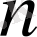 өлшемді кеңістік) болсын. Егер
өлшемді кеңістік) болсын. Егер
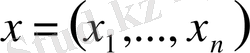 және
және
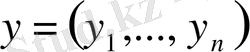 бұл кеңістіктің кез келген екі нүктесі болсы, онда
бұл кеңістіктің кез келген екі нүктесі болсы, онда
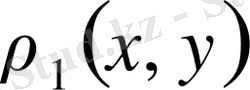 метрикасын мына өрнекпен
метрикасын мына өрнекпен
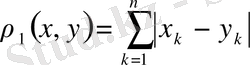
анықтауға болады, себебі
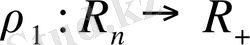 жоғарыдағы шарттарын қанағаттандырады. Олай болса,
жоғарыдағы шарттарын қанағаттандырады. Олай болса,
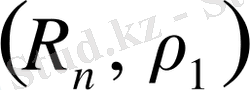 - метрикалық кеңістік.
- метрикалық кеңістік.
 . Егер
. Егер
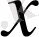 пен
пен
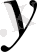 нүктелері берілген болса, онда
нүктелері берілген болса, онда
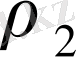 ара қашықтығын
ара қашықтығын
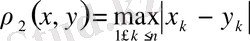
өрнегі бойынша да анықтауға болады. Олай болса,
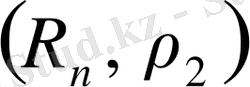 - метрикалық кеңістік.
- метрикалық кеңістік.
 .
.
 - нақты сандар жиыны болсын,
- нақты сандар жиыны болсын,
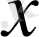 пен
пен
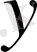 нүктелерінің ара қашықтығын
нүктелерінің ара қашықтығын
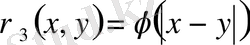 өрнегі бойынша анықтауға болады. Мұндағы
өрнегі бойынша анықтауға болады. Мұндағы
 барлық
барлық
 үшін анықталған, екі рет үзіліссіз дифференциалданатын, монотонды өспелі
үшін анықталған, екі рет үзіліссіз дифференциалданатын, монотонды өспелі
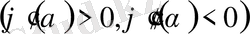 және
және
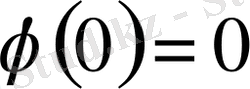 болатын функция. Бастапқы 1), 2) қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
болатын функция. Бастапқы 1), 2) қасиеттерін тексеру қиын емес, ал үшбұрыш теңсіздігі
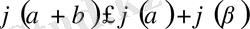 қатынасынан шығады. Сондықтан
қатынасынан шығады. Сондықтан
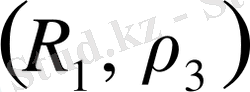 метрикалық кеңістік. Егер
метрикалық кеңістік. Егер
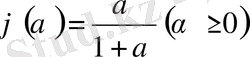 деп алсақ, онда
деп алсақ, онда
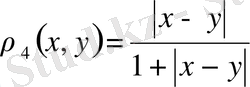
өрнегі де 1) - 3) шарттарын қанағаттандырады. Олай болса,
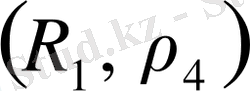 - метрикалық кеңістік. Бұл жағдайда
- метрикалық кеңістік. Бұл жағдайда
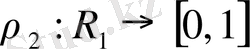 .
.
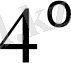 . Комплекс сандар жазықтығындағы радиус бірге тең ашық дөңгелектің
. Комплекс сандар жазықтығындағы радиус бірге тең ашық дөңгелектің
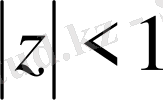 екі нүктесі -
екі нүктесі -
 мен
мен
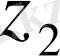 нүктелерінің ара қашықтығын
нүктелерінің ара қашықтығын
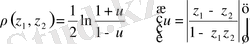
өрнегімен анықтауға болады. Метрикалық кеңістіктің аксиомалары орындалуы себепті бұл метрикалық кеңістік.
Бастапқы үш мысалдағы кеңістіктер векторлық (сызықтық) кеңістіктер болса, соңғы мысалдағы кеңістігіміз сызықты емес метрикалық кеңістік.
 .
.
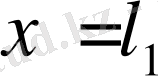 ; бұл жиынның нүктелері
; бұл жиынның нүктелері
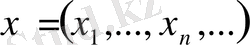
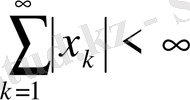
шартын қанағаттандыратын (яғни абсолют жинақталатын қатарлар) сан тізбектері. Егер
 (мұндағы
(мұндағы
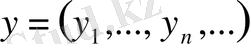 болса, онда метриканы
болса, онда метриканы
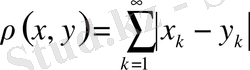
өрнегімен анықтауға болады. Бұл жағдайда да бастапқы екі қасиет оңай тексеріледі, ал үшіншісін былай тексеруге болады. Егер
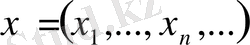 және
және
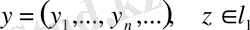 болса, онда кез келген
болса, онда кез келген
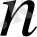 үшін
үшін
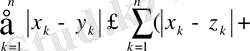
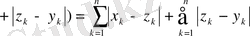 теңсіздігінен шекке көшу арқылы
теңсіздігінен шекке көшу арқылы
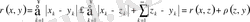 теңсіздігін алуға болады. Олай болса,
теңсіздігін алуға болады. Олай болса,
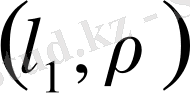 - метрикалық кеңістік. Кейде бұл кеңістікті
- метрикалық кеңістік. Кейде бұл кеңістікті
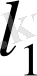 арқылы ғана белгілейтін боламыз.
арқылы ғана белгілейтін боламыз.
 .
.
 болсын. Бұл жиынның нүктелері
болсын. Бұл жиынның нүктелері
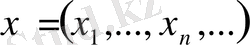
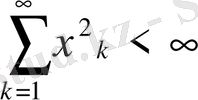
шартын қанағаттандыратын сан тізбектері.
Метриканы
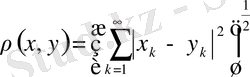
өрнегімен анықтауға болады.
 .
.
 болсын. Бұл жиынның нүктелері
болсын. Бұл жиынның нүктелері
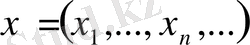 ,
,
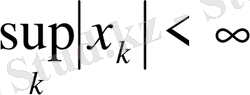 шартын қанағаттандыратын сандар тізбегі. Егер
шартын қанағаттандыратын сандар тізбегі. Егер
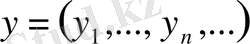 ,
,
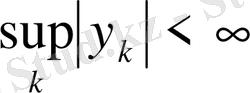 шартын қанағаттандыратын екінші бір кез келген сандар тізбегі болса, онда метриканы
шартын қанағаттандыратын екінші бір кез келген сандар тізбегі болса, онда метриканы
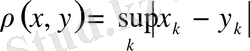 өрнегі бойынша алуға болады, себебі
өрнегі бойынша алуға болады, себебі
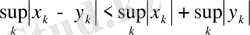 теңсіздігінен оның мағынасы болатыны шығады. Метриканың 1) - 2) аксиомалары бұл жағдайда да тез тексеріледі, ал 3) аксиомасын
теңсіздігінен оның мағынасы болатыны шығады. Метриканың 1) - 2) аксиомалары бұл жағдайда да тез тексеріледі, ал 3) аксиомасын
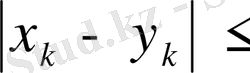
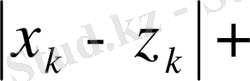
 теңсіздігінен алуға болады. Сонымен
теңсіздігінен алуға болады. Сонымен
 - метрикалық кеңістік, оны шектелген сан тізбектері кеңістігі деп атайды.
- метрикалық кеңістік, оны шектелген сан тізбектері кеңістігі деп атайды.
А н ы қ т а м а. Егер оның толықтыруы ашық болса, онда метрикалық кеңістікте жиын тұйық деп аталады.
А н ы қ т а м а.
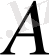 және
және
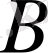
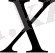 метрикалық кеңістіктегі екі жиын болсын. Егер
метрикалық кеңістіктегі екі жиын болсын. Егер
 болса, онда
болса, онда
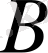 -да
-да
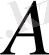 жиыны тығыз деп аталады. Егер
жиыны тығыз деп аталады. Егер
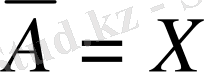 болса, онда
болса, онда
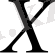 -та
-та
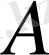 жиыны барлық жерде тағыз деп аталады.
жиыны барлық жерде тағыз деп аталады.
1. 3. Нормаланған кеңістік
А н ы қ т а м а.
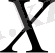 векторлық кеңістігінің әрбір элементіне теріс емес нақты санды сәйкес қоятын ережені
векторлық кеңістігінің әрбір элементіне теріс емес нақты санды сәйкес қоятын ережені
 арқылы белгілеп, ол төмендегідей шарттарды (аксиомаларды) :
арқылы белгілеп, ол төмендегідей шарттарды (аксиомаларды) :
1)
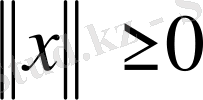 және
және
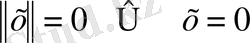 ;
;
2)
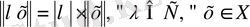 ;
;
3)
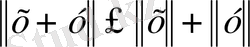
қанағаттандырса, онда ол ереже норма деп, ал кеңістіктің өзі нормаланған векторлық кеңістік деп аталады.
Теріс емес
 нақты санды
нақты санды
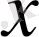 элементінің (векторының) ұзындығы деп қарастыруға болады. Ұзындығы бірге тең
элементінің (векторының) ұзындығы деп қарастыруға болады. Ұзындығы бірге тең
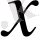 векторын
нормаланған вектор
деп атайды.
векторын
нормаланған вектор
деп атайды.
Нормаланған
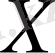 кеңістігінде
кеңістігінде
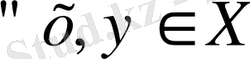 үшін
үшін
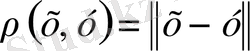 өрнегімен метрика анықтасақ, онда ол метрикалық кеңістік болады. Егер норма бойынша анықталған метриканы пайдалансақ, онда тізбектің шегі және оның жинақталуы мынадай:
өрнегімен метрика анықтасақ, онда ол метрикалық кеңістік болады. Егер норма бойынша анықталған метриканы пайдалансақ, онда тізбектің шегі және оның жинақталуы мынадай:
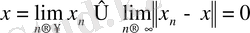 немесе
немесе
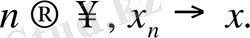
Осыған байланысты нормаланған кеңістіктегі жинақталуды норма бойынша жинақталуы деп атайды.
Метрикалық кеңістіктегідей нормаланған кеңістікті де бірнеше норма анықталуы мүмкін, бұл жағдайда оларды
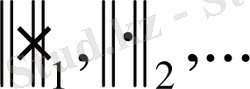 арқылы белгілейді.
арқылы белгілейді.
Норманың мына қасиеттерін
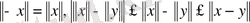 атап өтейік: бұларды дәлелдеу қиын емес.
атап өтейік: бұларды дәлелдеу қиын емес.
Нормаланған
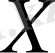 кеңістігіндегі шар (тұйық шар)
кеңістігіндегі шар (тұйық шар)
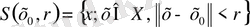
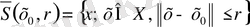
жиындары арқылы анықталады. Бұдан нормаланған кеңістікте метрикалық кеңістіктегі барлық түсініктердің орындалатыны шығады.
М ы с а л.
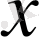 элементінің нормасы
элементінің нормасы
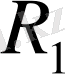 -де
-де
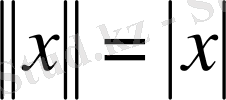 ,
,
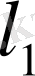 -де
-де
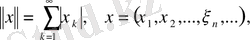
 -де
-де
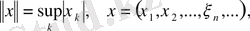
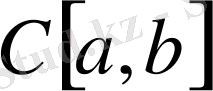 -да
-да
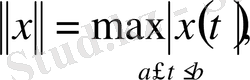
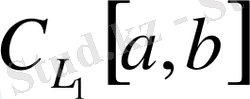 -да
-да
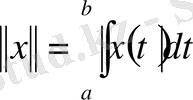
өрнектерімен анықталады.
Басқа кеңістіктерден
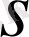 кеңістігінің бір айырмашылығы - онда
кеңістігінің бір айырмашылығы - онда
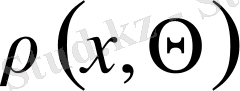 -ны, норманың 2) аксиомасы орындалмауына байланысты, норма ретінде қабылдауға болмайды.
-ны, норманың 2) аксиомасы орындалмауына байланысты, норма ретінде қабылдауға болмайды.
Негізгі алгебралық амалдардың нормаланған кеңістікте үзіліссіздігін көрсетейік:
а) Егер
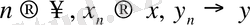 болса, онда
болса, онда
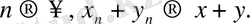 Шынында да,
Шынында да,
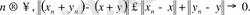
ә) Егер
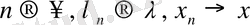 болса, онда
болса, онда
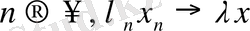 . Шынында да
. Шынында да

Нормаланған кеңістіктің маңыздысы - тұйық векторлық, яғни өзінің шектік нүктелерін қамтитын, ішкі кеңістіктер. Ақырлы өлшемді кеңістікте кез келген ішкі кеңістік тұйық. Ал ақырсыз өлшемді кеңістікте, төмендегі мысал көрсететіндей, бұл жағдай бола бермейді.
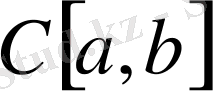 кеңістігінде бірқалыпты норма бойынша дәрежелері
кеңістігінде бірқалыпты норма бойынша дәрежелері
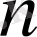 -нен аспайтын көпмүшелер жиыны тұйық емес ішкі кеңістікті құрайды.
-нен аспайтын көпмүшелер жиыны тұйық емес ішкі кеңістікті құрайды.
 кеңістігінде нөлден ерекше ақырлы санды компоненттері бар векторлар жиынды
кеңістігінде нөлден ерекше ақырлы санды компоненттері бар векторлар жиынды
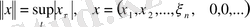 нормасы бойынша тұйық емес ішкі кеңістік құрады.
нормасы бойынша тұйық емес ішкі кеңістік құрады.
А н ы қ т а м а.
Нормаланған
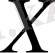 кеңістігінің ішкі кеңістігі деп оның кез келген тұйық векторлық ішкі жиынын айтады.
кеңістігінің ішкі кеңістігі деп оның кез келген тұйық векторлық ішкі жиынын айтады.
Нормаланған векторлық кеңістіктің мына леммадағы ішкі кеңістігінің қасиетін Рисс ашқан.
Л е м м а.
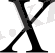 векторлық кеңістігінің, оның өзімен бірдей болмайтын, ішкі кеңістігі
векторлық кеңістігінің, оның өзімен бірдей болмайтын, ішкі кеңістігі
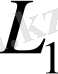 болсын. Онда кез келген
болсын. Онда кез келген
 үшін нормасы бірге тең
үшін нормасы бірге тең
 элементі табылып, барлық
элементі табылып, барлық
 үшін
үшін
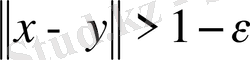 болады.
болады.
Д ә л е л д е у.
 ішкі кеңістігінде тиісті емес кез келген
ішкі кеңістігінде тиісті емес кез келген
 элементін алып,
элементін алып,
 деп белгілейік. Онда
деп белгілейік. Онда
 , себебі басқа жағдайда
, себебі басқа жағдайда
 жиынның шектік нүктесі ретінде
жиынның шектік нүктесі ретінде
 -дің өзіне тиісті болар еді. Ал бұл шарт бойынша мүмкін емес. Кез келген
-дің өзіне тиісті болар еді. Ал бұл шарт бойынша мүмкін емес. Кез келген
 саны үшін
саны үшін
 элементі табылып, төменгі шектің анықтамасы бойынша
элементі табылып, төменгі шектің анықтамасы бойынша
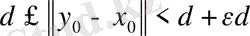 теңсіздігі орындалады. Егер
теңсіздігі орындалады. Егер
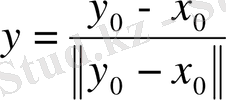
деп белгілесек, онда
 және
және
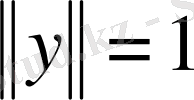 . Кез келген
. Кез келген
 үшін
үшін
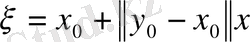 болсын. Онда
болсын. Онда
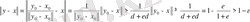
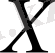 - векторлық кеңістік, ал
- векторлық кеңістік, ал
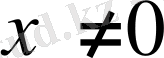 болсын. Онда
болсын. Онда
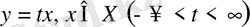 элементтері жиынын түзу деп, ал
элементтері жиынын түзу деп, ал
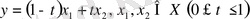 элементтер жиынын
элементтер жиынын
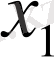 мен
мен
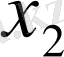 нүктелерін қосатын
кесінді
деп атайды.
нүктелерін қосатын
кесінді
деп атайды.
 кеңістігінің А жиыны өзінің екі нүктесімен қатар оларды қосатын кесіндіні де қамтитын болса, онда ол жиынды
дөңес жиын
деп атайды.
кеңістігінің А жиыны өзінің екі нүктесімен қатар оларды қосатын кесіндіні де қамтитын болса, онда ол жиынды
дөңес жиын
деп атайды.
Нормаланған кеңістікте шардың дөңес болу қасиеті соншалықты, тіпті оны үшбұрыш аксиомасына ауыстыруға болады.
Шынында да, егер нөлден ерекше
 болса, онда
болса, онда
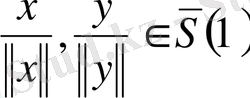 . Сондықтан
. Сондықтан
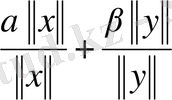 (мұнда
(мұнда
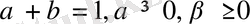 ) элементі
) элементі
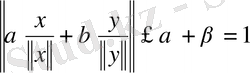 теңсіздігін қанағаттандыруына байланысты
теңсіздігін қанағаттандыруына байланысты
 шарының нүктесі болады. Егер
шарының нүктесі болады. Егер
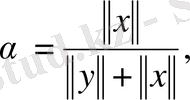
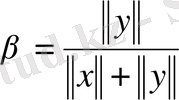
деп алсақ, онда
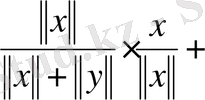
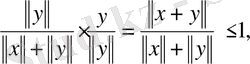
бұдан
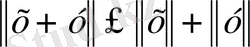 үшбұрыш теңсіздігі шығады.
үшбұрыш теңсіздігі шығады.
Енді нормаланған кеңістікте бірнеше нормалар анықталған жағдайды қарастырайық.
А н ы қ т а м а.
Векторлық нормаланған
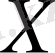 кеңістігінде
кеңістігінде
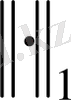 және
және
 нормалары берілсін. Егер
нормалары берілсін. Егер
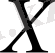 -тегі
-тегі
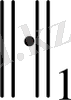 норма бойынша жинақталатын кез келген тізбек
норма бойынша жинақталатын кез келген тізбек
 норма бойынша да жинақталатын, және керісінше де, болса, онда
норма бойынша да жинақталатын, және керісінше де, болса, онда
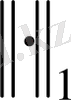 және
және
 нормаларын
өзара эквивалентті нормалар
деп атайды.
нормаларын
өзара эквивалентті нормалар
деп атайды.
Т е о р е м а. Ақырлы өлшемді векторлық кеңістікте кез келген екі норма өзара эквивалентті. Ондағы қарастырылып отырған норма бойынша тек жалғыз ғана ашық жиындар, тұйық жиындар т. т. жүйесі бар болады.
Дәлелдеу. Нормалардың эквиваленттігі транзитивті болуынан кез келген
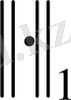 норма Евклид нормасына
норма Евклид нормасына
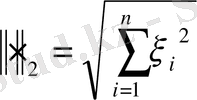
(мұндағы
 кейбір
кейбір
 базасындағы
базасындағы
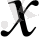 векторының координаттары) эквивалентті болатынын көрсету жеткілікті.
векторының координаттары) эквивалентті болатынын көрсету жеткілікті.
Кез келген
 үшін
үшін
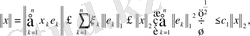 (1) (
(1) (
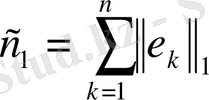 ), кез келген
), кез келген
 үшін
үшін
 табылып,
табылып,
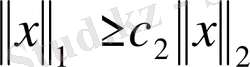 теңсіздіктері орындалатынын көрсетейік.
теңсіздіктері орындалатынын көрсетейік.
Қарсы жорып
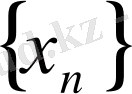 тізбегі үшін
тізбегі үшін
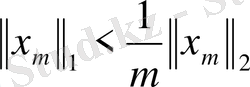 теңсіздігі орындалсын делік. Егер
теңсіздігі орындалсын делік. Егер
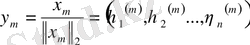 деп белгілесек, онда
деп белгілесек, онда
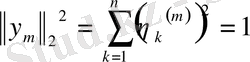 (2)
(2)
болады. Сондықтан кез келген
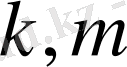 үшін
үшін
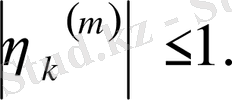
Евклид кеңістігіндегі шар жинақы болатынынан
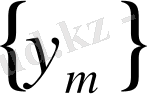 тізбегінен жинақталатын тізбекше бөліп алуға болады. Жаңадан белгілеулер енгізбеу үшін сол
тізбегінен жинақталатын тізбекше бөліп алуға болады. Жаңадан белгілеулер енгізбеу үшін сол
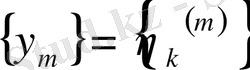 тізбегінің өзі кейбір
тізбегінің өзі кейбір
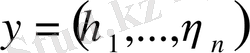 векторына жинақталады деп есептейміз. Бұл жағдайда
векторына жинақталады деп есептейміз. Бұл жағдайда
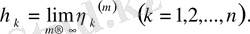
(2) теңдікті шекке көшсек, онда
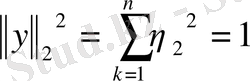 шығады да
шығады да
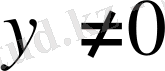 . Бірақ (1) теңсіздік бойынша
. Бірақ (1) теңсіздік бойынша
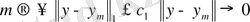 болады. Ал екінші жағынан
болады. Ал екінші жағынан

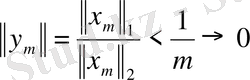
болады да
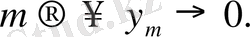 Шыққан қайшылық теореманы дәлелдейді.
Шыққан қайшылық теореманы дәлелдейді.
Метрикалық кеңістіктің маңызды қасиеттерінің бірі оның толық болуы. Сәйкес түсінік нормаланған кеңістікте де бар.
А н ы қ т а м а. Нормаланған толық векторлық кеңістікті Банах кеңістігі немесе В кеңістігі деп атайды. Кейде мұндай кеңістікті В типтес кеңістік деп те атайды.
1. 4. Гильберт кеңістігі
1 - анықтама.
Келесі қасиеттерді иемденетін
 жиынының
жиынының
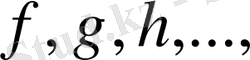 элементтері
Гильберт кеңістігі
деп аталады
элементтері
Гильберт кеңістігі
деп аталады
1)
 сызықты кеңістік болып табылады, яғни
сызықты кеңістік болып табылады, яғни
 -та элементтерді құру амалдары және оларды нақты немесе комплексті сандарға көбейту анықталған (осыған тәуелді
-та элементтерді құру амалдары және оларды нақты немесе комплексті сандарға көбейту анықталған (осыған тәуелді
 нақты немесе комплексті кеңістік деп аталады) ;
нақты немесе комплексті кеңістік деп аталады) ;
2)
 -та скалярлы көбейтінді енгізілген, яғни аксиомаларды қанағаттандыратын
-та скалярлы көбейтінді енгізілген, яғни аксиомаларды қанағаттандыратын
 және
және
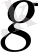 аргументтер парынан
аргументтер парынан
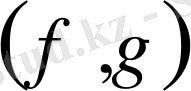 сандық функция:
сандық функция:
а) Кез келген
 саны үшін
саны үшін
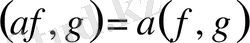 ;
;
б)
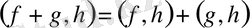 ;
;
в)
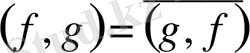 , мұндағы сызық комплексті түйіндесті білдіреді;
, мұндағы сызық комплексті түйіндесті білдіреді;
г)
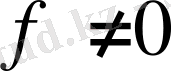 үшін
үшін
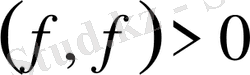 ;
;
 үшін
үшін
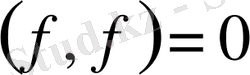 ;
;
3)

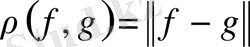 ара қашықтығына қатысты толық метрикалық кеңістік болып табылады, мұндағы кез келген
ара қашықтығына қатысты толық метрикалық кеңістік болып табылады, мұндағы кез келген
 элементі үшін оның нормасы
элементі үшін оның нормасы
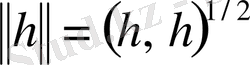 қатынастан анықталады.
қатынастан анықталады.
Кейбір мысалдар келтірейік.
М ы с а л д а р.
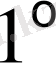 . Гильберт кеңістігінің қарапайым мысалы болып шекті өлшемді
. Гильберт кеңістігінің қарапайым мысалы болып шекті өлшемді
 сызықты кеңістігі табылады, егер онда 1-анықтамадағы 2 аксиоманы қанағаттандыратын болса.
сызықты кеңістігі табылады, егер онда 1-анықтамадағы 2 аксиоманы қанағаттандыратын болса.
 . Элементтері
. Элементтері
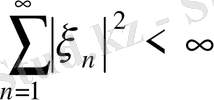 ,
,
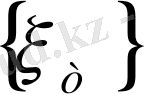 сандар тізбегі болып табылатын,
сандар тізбегі болып табылатын,
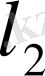 кеңістігін қарастырамыз. Бұл кеңістікте сызықты операция міндетті түрде анықталады: егер
кеңістігін қарастырамыз. Бұл кеңістікте сызықты операция міндетті түрде анықталады: егер
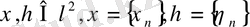 болса, онда
болса, онда
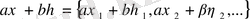 , мұндағы
, мұндағы
 және
және
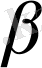 - кейбір сандар.
- кейбір сандар.
Бұл кеңістікке
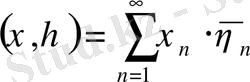
формула бойынша
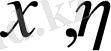 элементтерінің скалярлы көбейтіндісін енгіземіз.
элементтерінің скалярлы көбейтіндісін енгіземіз.
Коши - Буняковский теңсіздігі бойынша
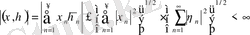
аламыз. Сондықтанда скалярлы көбейтіндіні берілген ереже бойынша енгізуге болады. Және сол сияқты скалярлы көбейтіндінің барлық аксиомаларының дұрыстығына көз жеткізу қиын емес.
Осылайша,
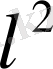 - гильберт кеңістігі.
- гильберт кеңістігі.
 .
.
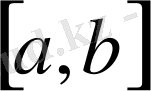 кесіндісінде Лебег функциясы бойынша модульдің квадратымен интегралданатын
кесіндісінде Лебег функциясы бойынша модульдің квадратымен интегралданатын
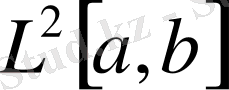 жиынын қарастырамыз. Жиындардың өлшемін Лебег бойынша интегралдағанда нөлді елемеуге болатын болғандықтан, шындығында да
жиынын қарастырамыз. Жиындардың өлшемін Лебег бойынша интегралдағанда нөлді елемеуге болатын болғандықтан, шындығында да
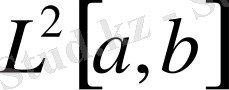 өзара эквивалентті функциялар классы болып табылады.
өзара эквивалентті функциялар классы болып табылады.
Бұл кеңістікте сызықты операцияны енгізуге болады - қарапайым функцияны құру және функцияны санға көбейту.
Бұл кеңістікте скалярлы көбейтінді
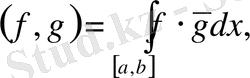 мұндағы
мұндағы
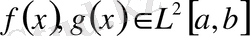
ереже бойынша енгізіледі.
Егер
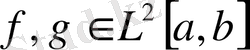 болса, онда
болса, онда
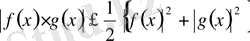 теңсіздіктен
теңсіздіктен
 көбейтінді де
көбейтінді де
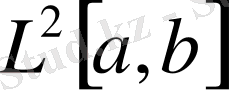 тиісті екендігі шығады. Скалярлы көбейтіндінің аксиомасы тікелей нәтиже бойынша Лебег интегралының қасиетінен тексеріледі. Осылайша,
тиісті екендігі шығады. Скалярлы көбейтіндінің аксиомасы тікелей нәтиже бойынша Лебег интегралының қасиетінен тексеріледі. Осылайша,
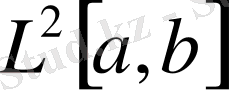 - гильберт кеңістігі.
- гильберт кеңістігі.
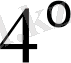 .
.
 - нормаланған кеңістік болсын. Бұдан мынадай сұрақ туады: қандай қосымша шарттармен кейбір скалярлы көбейтінді анықталатын
- нормаланған кеңістік болсын. Бұдан мынадай сұрақ туады: қандай қосымша шарттармен кейбір скалярлы көбейтінді анықталатын
 -да норма қанағаттандыруы қажет? Ол үшін кез келген
-да норма қанағаттандыруы қажет? Ол үшін кез келген
 және
және
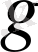 екі элементтер үшін
екі элементтер үшін
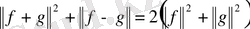
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz