Атом құрылысы мен спектрлері: сутегі спектрі, Бальмер-Ридберг заңы және Томсон-Резерфорд модельдері


І БӨЛІМ
АТОМНЫҢ ҚҰРЫЛЫСЫ. БОР ТЕОРИЯСЫ
§1. 1. Сутегі атомының сызықтық спектрі
Зерттеулер көрсеткендей, білгілі бір заттың қатты және газ тәрізді күйдегі сәуле шығару спектрлері елеулерліктей бір-бірінен өте өзгеше болады. Жоғары температураға дейін қызды-рылған қатты (немесе сұйық ) күйдегі кез келген зат, мысалы металл бүкіл мүмкін жиілікті жарықты шығарады және оның сәуле шығару спектрі тұтас спектр болып табылады (1. 1. 1-сурет) . Осы металдың газ тәрізді күйінің, яғни металл буының немесе сирексітілген түрдегі оқшауланған газ атомдары жеке спектрлік сызықтардан тұратын спектрді шығарады. Осыған сәйкес атомдардың шығару спектрі сызықтық спектр деп аталады. Сызықтық спектрде энергияның таралу мысалы 1. 1. 2-суретте келтірілген.
Атомық спектрлерді зерттеу атомдардың құрылысын танып білудің негізгі себепкері болды. Ең алдымен, атомдардың спек-трлеріндегі сызықтар ретсіз орналаспағаны, олар сызықтар легі деп аталатын топқа бірігетіні белгілі болды. Әсіресе осы сы-зықтар легі сутегі спектрінде анық көрінеді. Бұл спектр 1. 1. 3-суретте келтірілген: спектрдің көрінетін учаскесінің сызықтары тұтас, ал ультракүлгін аймаққа жуық жағы үзік болып бейне-ленген. Сутегі спектрінің көрінетін учаскесінде төрт сызық бар: қызыл, көгілдір, көк, күлгін және т. б. Бұл сызықтарды Н α , Н β , Н γ , Н δ деп белгілеу қабылданған.
Швейцария физигі Бальмер (1885 ж. ) Н α , Н β , Н γ , Н δ сызықтарға сәйкес келетін толқын ұзындықтар 1. 1. 1 таблицада көрсетілгендей өр-нектелуі мүмкін екендігін байқады (аңғарды) . Бальмер мұндағы λ 0 ша-маны « негізгі сан » деп атады. Баль-мер байқаған заңдылықтың мағына-сы мынада: егер осы таблицадағы 4/3 және 9/8 бөлшектер 16/12 және 36/32 сияқты келтірілсе, онда бөл-шектердің алымдары сандар бір-ізділігінің натурал қатарын (3 2 , 4 2 , 5 2 , 6 2 ), ал бөлімдері квадраттар айы-рымының бірізділігін құрайды: 3 2 −2 2 , 4 2 −2 2 , 5 2 −2 2 , 6 2 −2 2 . Нәтиже-сінде Бальмерге жоғарыда көрсетіл-ген төрт сызықтың толқын ұзындық-тары үшін эмпирикалық (яғни тәжі-рибеге негізделген) формуланы жа-зудың сәті түсті:
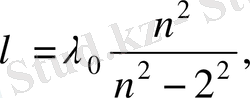 (1. 1. 1)
(1. 1. 1)
мұндағы
п
белгілеу
Н
α
,
Н
β
,
Н
γ
,
Н
δ
сызықтарға сәйкес
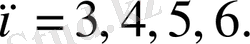 λ
0
шама 364, 56 нм тең болып шыққан
λ
0
шама 364, 56 нм тең болып шыққан
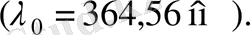
Көп кешікпей (ХХ ғ-ң басында) сутегі атомының спектрінде тағы да бірнеше лек табылды. Бүкіл осы сызықтардың толқын ұзындықтары да Бальмер формуласына бағынады. Бальмер фор-муласындағы ең маңыздысы, формула бөлімінің бүтін сандар квадраты айырымы түрінде көрсетілуі. Бес жылдан соң (1890 ж. ) швед ғалымы И. Ридберг
 толқындық сан
1 (
толқындық сан
бірлік ұзындыққа қанша толқын ұзындықтың сиятынын көрсетеді) үшін Бальмер формуласын «төңкерілген түрде» жа-зып қазіргі уақыттағы түрді берді:
толқындық сан
1 (
толқындық сан
бірлік ұзындыққа қанша толқын ұзындықтың сиятынын көрсетеді) үшін Бальмер формуласын «төңкерілген түрде» жа-зып қазіргі уақыттағы түрді берді:
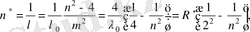 (1. 1. 2)
(1. 1. 2)
мұндағы
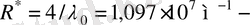 Ридберг тұрақтысы.
Ридберг тұрақтысы.
п
-
нің
әртүрлі мәндерімен өзгешеленетін спектрлік сызықтар
Бальмер легі
деп аталатын топты немесе сызықтар легін құрай-тыны (1. 1. 2) Бальмер-Ридберг формуласынан көрініп тұр.
п
-
нің
өсуімен бірге лектің спектрлік сызықтары бір-біріне жақындай-ды, яғни ұзын толқындардан қысқа толқындарға өтуіне қарай сызықтар аралығындағы қашықтық заңға сыйымды кемиді. Ақырында, Бальмер легінің спектрлік сызықтары ультракүлгін (УК) аймақта жалғасатыны және
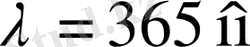 толқын ұзындықта аяқталатыны белгілі болды (1. 1. 3-сурет) .
толқын ұзындықта аяқталатыны белгілі болды (1. 1. 3-сурет) .
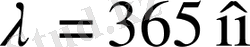 толқын ұзын-дық маңында спектрлік сызықтардың қоюланатыны соншалық, тіпті оларды айырып білу қиын. Бірақ
толқын ұзын-дық маңында спектрлік сызықтардың қоюланатыны соншалық, тіпті оларды айырып білу қиын. Бірақ
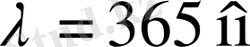 кездегі Баль-мер легінің шегі
кездегі Баль-мер легінің шегі
 сәйкес келеді, яғни формуладағы
сәйкес келеді, яғни формуладағы

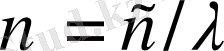 болғандықтан (1. 1. 2) формуланы жиілік үшін былай жазуға болады:
болғандықтан (1. 1. 2) формуланы жиілік үшін былай жазуға болады:
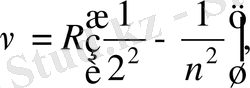 (1. 1. 3)
(1. 1. 3)
мұндағы
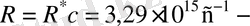 бұл да Ридберг тұрақтысы.
бұл да Ридберг тұрақтысы.
(1. 1. 3) формуланы пайдаланып
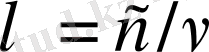 өрнегі бойынша сәй-кес сызықтардың толқын ұзындықтарын есептеуге болады. Экс-перимент мәліметтерімен салыстырылған осы толқын ұзындық-тардың есептелген мәндері 1. 1. 2 таблицада келтірілген.
өрнегі бойынша сәй-кес сызықтардың толқын ұзындықтарын есептеуге болады. Экс-перимент мәліметтерімен салыстырылған осы толқын ұзындық-тардың есептелген мәндері 1. 1. 2 таблицада келтірілген.
Сутегінің көрінетін және ультракүлгін аймақтарға жуық спектрі сызықтарының толқын ұзындықтарын есептеу нәтиже-лері Бальмер-Ридберг формуласы бойынша алынған мәндерімен өте жақсы сәйкес келді. Ал бұл, сутегі спектрінің басқа да ай-мақтарын зерттеуге ғалымдарға түрткі болды. Ғалымдардың бұл зерттеулері сәтті аяқталды. Спектрдің инфрақызыл бөлігінде
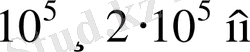 толқын ұзындықтар аймағында спектрлік сы-зықтар легі табылды. Мұндай спектрлік сызықтар легі үшін Бальмер-Ридберг формуласы келесі түрде жазылады:
толқын ұзындықтар аймағында спектрлік сы-зықтар легі табылды. Мұндай спектрлік сызықтар легі үшін Бальмер-Ридберг формуласы келесі түрде жазылады:
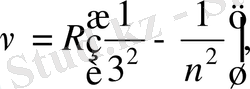
мұндағы
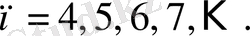 Бұл Пашен легі.
Бұл Пашен легі.


 − ангстрем2
− ангстрем2
1916 ж. Лайман
 сәйкес келетін сызықтар легін, ал 1922 ж. Брэкет
сәйкес келетін сызықтар легін, ал 1922 ж. Брэкет
 мәнге сәйкес сызықтар легін тапты. Пфунд 1924 ж.
мәнге сәйкес сызықтар легін тапты. Пфунд 1924 ж.
 сай келетін лекті анықтады.
сай келетін лекті анықтады.
Сонымен, спектрдің ультракүлгін аймағында Лайман легі
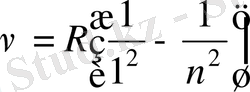
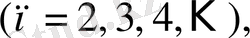
спектрдің инфрақызыл аймағында келесі спектрлер анықталды:
Пашен легі
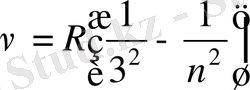
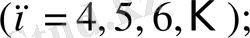
Брэкет легі
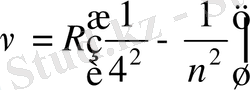
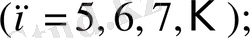
Пфунд легі
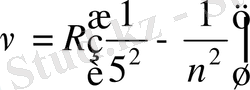
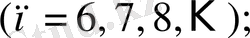
Хэмфри легі
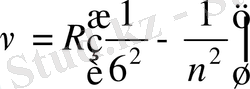
5
4
3
2
1
1
1
1
94
97
103
122
7
6
5
4
3
2
2
2
2
2
397
410
434
486
656
7
6
5
4
3
3
3
3
1005
1094
1282
1875
7
6
5
4
4
4
2165
2625
4051
7
6
5
5
4652
7458
Осы келтірілген сутегі атомы спектріндегі лектерді Баль - мердің қорытылып жазылған формуласы деп аталатын бір ғана формуламен сипаттауға болады:
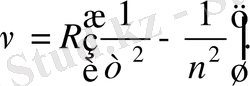 (1. 1. 4)
(1. 1. 4)
Әрбір берілген лек үшін мұндағы
т
-
нің
тұрақты мәні бар:
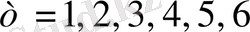 (
лектерді анықтайды
), ал
п
бүтін санды мән-дерді
(
лектерді анықтайды
), ал
п
бүтін санды мән-дерді
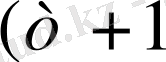 бастап) қабылдайды (
осы лектің жеке сызықтарын анықтайды
) .
бастап) қабылдайды (
осы лектің жеке сызықтарын анықтайды
) .
Лектер бойынша сызықтардың таралуы мен лектер фор-мулалары ұзақ уақыт бойы түсіндірілімін таппады және жұм-бақты болды. Бальмердің ашқан жаңалығы өзінің түсіндірілімін 28 жыл күтті. Бұларды түсіну үшін атомның құрылысы туралы түсінікті білу қажет болды. Бұл түсінік ағылшын физигі Э. Резерфорд еңбектерінен бастау алды.
Сутегі атомының спектрі 1. 1. 3 таблицада келтірілген.
§1. 2. Томсон атомының моделі.
Атомның ядролық моделі. Резерфорд тәжірибесі
1896 ж. А. Беккерель радиоактивті құбылысты ашқаннан соң ғалымдарға атомның құрылысын зерттеуге мүмкіндік беретін нәзік құрал табылды. Мұндай құрал: массасы іс жүзінде гелий атомының массасына тең, заряды оң және абсолют шамасы бойынша электронның екі зарядына тең, ауыр радиоактивті эле-менттерден (уран, радий және т. б. ) өте үлкен жылдамдықпен шығатын α -бөлшектер.
Заттың бөлінбейтін ең кішкентай бөлшектері ретінде атом-дар («атомос» − ыдырамайтын) туралы түсінік көне (арғы) за-манда пайда болды.
Электрон кез келген заттың ең негізгі құрамды бөлігінің бірі болып табылатыны ХІХ ғ-ң екінші жартысында эксперимент жүзінде дәлелденді. Осындай дәлелдер және көптеген экспери-мент мәліметтері ХХ ғ-ң басында атомның құрылысы туралы мәселеге алып келді.
Оқшауланған атом шығаратын сәуле спектрінің сипатын тү-сіндіру үшін, сәуле шығаратын осы атомның ішіндегі электрон гармониялық тербеліс жасайды деп ұйғару қажет, демек, қайсы-бір сыртқы әсер салдарынан тепе-теңдік қалпынан шығарылған электрондар
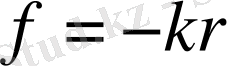 (мұндағы
r
− электронның тепе-теңдік қал-пынан ауытқуы) түріндегі казисерпімді күшпен тепе-теңдік қал-пы төңірегінде ұсталынып үздіксіз тербелмелі қозғалыста бола-ды. Сөйтіп, осы гармониялық тербелістердің нәтижесінде атом қоршаған кеңістікке электрмагниттік энергияны шығарады.
(мұндағы
r
− электронның тепе-теңдік қал-пынан ауытқуы) түріндегі казисерпімді күшпен тепе-теңдік қал-пы төңірегінде ұсталынып үздіксіз тербелмелі қозғалыста бола-ды. Сөйтіп, осы гармониялық тербелістердің нәтижесінде атом қоршаған кеңістікке электрмагниттік энергияны шығарады.
Атом теориясын құру үшін оның физикалық моделі қажет, яғни физикалық жүйе туралы сияқты атом туралы да түсініктің болуы шарт. Атомның алғашқы тарихи моделі ағылшын ғалымы Дж. Томсон 1903 ж. құрған және «тамшы» моделі деген атау ал-ған модель болды. Томсон былай деп жорамалдады:
атом
,
бүкіл көлемі оң зарядтармен үздіксіз біркелкі зарядталған шар болып саналады
;
осы «электрлік сұйық»
,
яғни шар ішінде өзінің тепе-теңдік төңірегінде тербелетін электрондар бар және элек
-
трондардың қосынды теріс зарядтары шардың оң зарядына тең
,
сондықтан
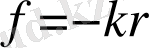 бүтіндей алғанда атом бейтарап
(1. 2. 1,
а
-сурет) . Электрон тепе-теңдік қалпынан ығысқанда, осы ығысуға пропорционал кері қайтарушы квазисерпімді күш пайда болады деп көрсетті Дж. Дж. Томсон. Ал бұл гар-мониялық тербелістердің жал-пы шарты. Гармониялық тер-белістер жасайтын электрондар Максвелл теориясы бойынша, тербеліс жиіліктері электрондардың тербеліс жиілігіне тең мо-нохроматты электрмагниттік толқындарды шығаруы керек. Атомдардың айрықша ерекшеліктерін −
олар шығаратын жа
-
рық сәулесі спектрінің сызықтық сипатын
− Томсон осылай тү-сіндірді. Томсон моделінің негізінде Г. А. Лоренц дисперсияның электрондық теориясын құрды.
бүтіндей алғанда атом бейтарап
(1. 2. 1,
а
-сурет) . Электрон тепе-теңдік қалпынан ығысқанда, осы ығысуға пропорционал кері қайтарушы квазисерпімді күш пайда болады деп көрсетті Дж. Дж. Томсон. Ал бұл гар-мониялық тербелістердің жал-пы шарты. Гармониялық тер-белістер жасайтын электрондар Максвелл теориясы бойынша, тербеліс жиіліктері электрондардың тербеліс жиілігіне тең мо-нохроматты электрмагниттік толқындарды шығаруы керек. Атомдардың айрықша ерекшеліктерін −
олар шығаратын жа
-
рық сәулесі спектрінің сызықтық сипатын
− Томсон осылай тү-сіндірді. Томсон моделінің негізінде Г. А. Лоренц дисперсияның электрондық теориясын құрды.
Томсон атомындағы электронның тербелу процесін 1. 2. 1, б-суретте келтірілген схема бойынша қарастырайық. Шардың ішкі бөлігі оның центрінен r қашықтықта болатын электронға
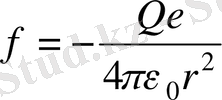
(мұндағы
Q
− шардың ішкі бөлігінің заряды) күшпен әсер етеді.
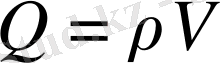 екені белгілі (мұндағы
ρ
− оң зарядтың көлемдік тығыз-дығы) .
екені белгілі (мұндағы
ρ
− оң зарядтың көлемдік тығыз-дығы) .
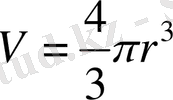 болғандықтан,
болғандықтан,
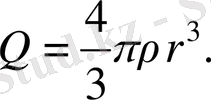 Демек,
Демек,
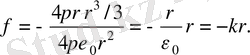
Сонымен, атом ішіндегі электронға әсер ететін күш электрон - ның атом центрінен ығысуына пропорционал және атом цен - тріне бағытталған . Кері қайтарушы күштің функциясын атқа-ратын осы «квазисерпімді күш» атом центрі арқылы өтетін түзу бойымен электронның тербелуіне себепші болып табылады. Сондықтан электрон атом ішінде
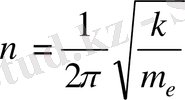
(мұндағы т е − электронның массасы) жиілікпен гармониялық тербеліс жасайды.
 Теріс зарядталған бөлшектердің тербелмелі сипаты туралы ой (идея) нәтижелі (жемісті) болып шықты және бірсыпыра құ-былыстарды түсіндіргенде сәтті пайдаланылды. Дегенмен, Том-сон моделі тұтастай алғанда күдік туғызды, өйткені оң және те-ріс зарядтардың орналасуы жайында айтылған Томсон пікірі ті-келей тәжірибеге негізделмеген. Бірнеше жылдан соң, атом ішінде оң зарядтардың үздіксіз таралатыны туралы түсініктің (яғни Томсон моделінің) қате екені дәлелденді.
Теріс зарядталған бөлшектердің тербелмелі сипаты туралы ой (идея) нәтижелі (жемісті) болып шықты және бірсыпыра құ-былыстарды түсіндіргенде сәтті пайдаланылды. Дегенмен, Том-сон моделі тұтастай алғанда күдік туғызды, өйткені оң және те-ріс зарядтардың орналасуы жайында айтылған Томсон пікірі ті-келей тәжірибеге негізделмеген. Бірнеше жылдан соң, атом ішінде оң зарядтардың үздіксіз таралатыны туралы түсініктің (яғни Томсон моделінің) қате екені дәлелденді.
Дж. Дж. Томсон шәкірттерінің бірі − ағылшын физигі Резер-форд атомдағы оң және теріс зарядтардың таралу сипатын анық-тау үшін өз қызметкерлерімен бірге 1911 ж. эксперимент жаса-ды. Эксперимент нәтижелері Томсон моделіне қарама-қайшы болып шықты. Резерфорд экспериментінде оң зарядты (+2 е ) α -бөлшектер шоғы өте жұқа (~0, 01мм) алтын қаңылтырға пер-пендикуляр бағытталып жіберіледі (1. 2. 2, а -сурет) . Сонда көпте-ген α -бөлшектер алтын қаңылтырдан емін-еркін өтіп кеткен. Әрбір бөлшек түскен жердегі экранның жарқылдауы бойынша қаңылтырдан өткен α -бөлшектер тіркелген. Экран бетінің жар-қылдауы микроскоп көмегімен де бақыланған және тіркелген. Бөлшектердің бірсыпыра пайызы 10°, 15°, 20°, … бұрыштарға ауытқитыны анықталды. Сонымен қатар, α -бөлшектердің аз-маз (болмашы) бөлігі қаңылтырдан кейін қарай серпілетіні, яғни ал-ғашқы қозғалыс бағытынан 90° бұрыштан үлкен (кейде тіпті 180° бұрышқа дейін дерліктей) бұрышқа ауытқитыны белгілі болды. Осы факт Резерфордты атомның ядролық моделі туралы идеяға алып келді.
Атомның Томсон моделі тұрғысынан бұл тәжірибе нәтиже-лерін түсіндіру мүмкін емес. Шынында да Томсон моделі бо-йынша жұқа қаңылтыр «қатты» шариктердің − бір-бірінен қай-сыбір қашықтықта жататын атомдардың жиынтығы болып сана-лады. Қаңылтыр айтарлықтай жұқа болғандықтан саны көп α -бөлшектердің басым көпшілігі бастапқы бағытынан ауытқы-май атомдардың арасымен кедергесіз өтіп кетуі керек, өйткені атом-дар электр бейтарап және α -бөлшектер іс жүзінде олармен өзара әсерлеспейді. Сонда экранда шамамен бөлшектер ағынының қи-масы бойынша жарқылдардың біркелкі таралуын күтуге болар еді. Алайда, Резерфордтың алған эксперименттік нәтижелері бұл болжамды жоққа шығарды.
α
-бөлшектердің шашырау ақиқаттығы (фактісі) және олар-дың қалайыдан серпілуі (кейде кері бағытта) атомның құрамын-да
α
-бөлшектерді өткізбейтін шомбал бөлік бар дегенге меңзеді. Осының негізінде Резерфорд былай деп ұйғарды:
атомның бү
-
кіл оң заряды және оның бүкіл
(
негізгі
)
массасы кішкентай көлемге −
атомның ядросында
− жинақталған
(атом массасы-ның 99, 9%)
.
Резерфордтың бағалауы бойынша (әртүрлі бұрышқа шашыраған
α
-бөлшектер санын есептеп) ядроның диаметрі
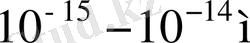 шамасында. Кинетикалық теориядан және әсіресе Эйнштейннің броундық қозғалысқа жүргізген талдауынан атом-ның өлшемі 10
−10
м деп бағаланды. Ал бұл, электрондар ядродан шамамен ядроның 10 000-
нан
100 000-
ға
дейінгі кесе-көлденең ендеріндей қашықтықта болуы тиіс дегенді білдіреді, демек атомның негізгі бөлігін бос кеңістік құрайды.
α
-бөлшек атоммен соқтығысқанда тек сирек жағдайларда ғана өзінің ұшу бағытын неліктен кенет өзгертетіні енді түсінікті болды. Бұл айтылған, атоммен соқтығысатын
α
-бөлшектің жолында шомбал ядро кез-десіп оның қозғалысына бөгет болатын аз ықтималды шартқа сәйкес келеді. Егер ядро
α
-бөлшектің түзусызықты траектория-сынан шет жатса, онда
α
-бөлшек атомнан өтіп кетеді.
шамасында. Кинетикалық теориядан және әсіресе Эйнштейннің броундық қозғалысқа жүргізген талдауынан атом-ның өлшемі 10
−10
м деп бағаланды. Ал бұл, электрондар ядродан шамамен ядроның 10 000-
нан
100 000-
ға
дейінгі кесе-көлденең ендеріндей қашықтықта болуы тиіс дегенді білдіреді, демек атомның негізгі бөлігін бос кеңістік құрайды.
α
-бөлшек атоммен соқтығысқанда тек сирек жағдайларда ғана өзінің ұшу бағытын неліктен кенет өзгертетіні енді түсінікті болды. Бұл айтылған, атоммен соқтығысатын
α
-бөлшектің жолында шомбал ядро кез-десіп оның қозғалысына бөгет болатын аз ықтималды шартқа сәйкес келеді. Егер ядро
α
-бөлшектің түзусызықты траектория-сынан шет жатса, онда
α
-бөлшек атомнан өтіп кетеді.
1. 2. 2, б-суретте ядро кішкентай шарик түрінде бейнеленген.
α
-бөлшектің қозғалыс траекториясы стрелкамен көрсетілген:
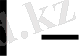 атом ядросы мен
α
-бөлшектің бастапқы қозғалыс бағыты арасындағы «нысана қашықтық»;
ϕ
−
α
-бөлшектің ауытқу бұры-шы. Осы суреттегі үш жағдайда да
α
-бөлшектің траекториясы, фокусында атом ядросы жататын
гипербола
пішінді болып табылады.
атом ядросы мен
α
-бөлшектің бастапқы қозғалыс бағыты арасындағы «нысана қашықтық»;
ϕ
−
α
-бөлшектің ауытқу бұры-шы. Осы суреттегі үш жағдайда да
α
-бөлшектің траекториясы, фокусында атом ядросы жататын
гипербола
пішінді болып табылады.
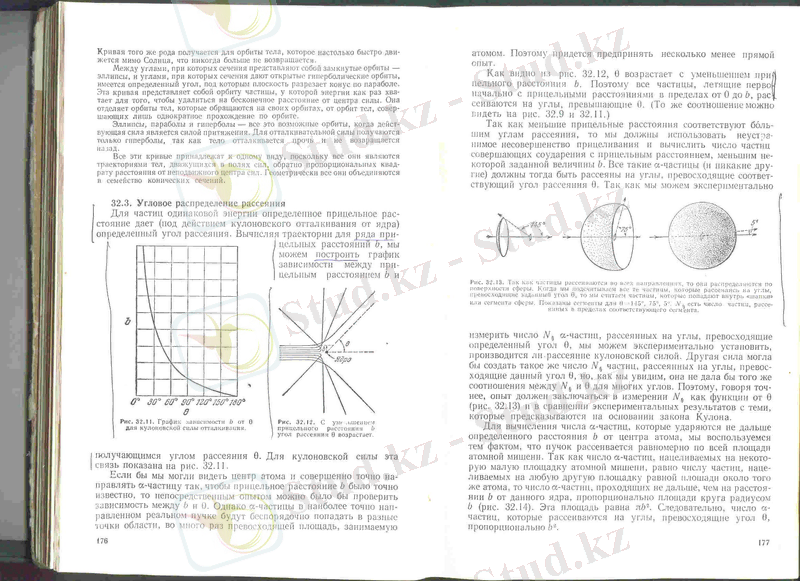
1. 2. 3-суреттен де байқайтынымыз-дай, α -бөлшек атом центріне неғұрлым жақын жерден өтсе, оның траекториясы да соғұрлым тік бола түседі. Егер υ жылдамдықпен ұшып келе жатқан α -бөлшек пен атом ядросының центрі бір түзудің бойында жатса ( α -бөлшектің υ жылдамдығы ядроға дәл бағытталған), онда α -бөлшек ядроға жақындаған са-йын, кулондық кері итеру күшті жеңу үшін оның кинетикалық энергиясы үзіліссіз кемиді де, қайсыбір r 0 қашықтықта α -бөл-шек тоқтап кері бұрылады. Яғни кинетикалық энергия α -бөл-шектің 2 е заряды мен ядроның Ze ( Z − Менделеев жүйесіндегі элементтің реттік номері, е − элементар заряд) зарядының өзара әсерлесу потенциалдық энергиясына айналады:
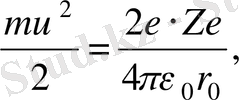 (1. 2. 1)
(1. 2. 1)
мұндағы т − α -бөлшектің массасы, υ − оның ядродан алыстағы бастапқы жылдамдығы.
 Ядро маңындағы
α
-бөлшектердің траекторияларын суреттеп сипаттайтын механикалық модель 1. 2. 4,
а
-суретте келтірілген.
α
-бөлшектің
Ядро маңындағы
α
-бөлшектердің траекторияларын суреттеп сипаттайтын механикалық модель 1. 2. 4,
а
-суретте келтірілген.
α
-бөлшектің
 -
ге
пропорцио-нал потенциалдық энергиясы бар, мұндағы
r
− ядродан қашықтық.
-
ге
пропорцио-нал потенциалдық энергиясы бар, мұндағы
r
− ядродан қашықтық.
Төмпешік, бетінің кез келген нүктесіндегі
h
биіктік
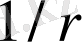 -
ге
пропорционал болатындай етіліп тұрғызылған (бұл жағдайда мұндағы
r
− жазықтықта жа-татын нүктенің центрден қашықтығы) . Демек, төмпешік бетіндегі шариктің
-
ге
пропорционал болатындай етіліп тұрғызылған (бұл жағдайда мұндағы
r
− жазықтықта жа-татын нүктенің центрден қашықтығы) . Демек, төмпешік бетіндегі шариктің
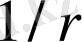 -
ге
пропорционал тартылыс потенциалдық энергиясы болады. Яғни ша-риктің қозғалысы, ядроның электр өрісіндегі жазықтықта қозғалатын заряд-тың қозғалысына ұқсас.
-
ге
пропорционал тартылыс потенциалдық энергиясы болады. Яғни ша-риктің қозғалысы, ядроның электр өрісіндегі жазықтықта қозғалатын заряд-тың қозғалысына ұқсас.
 Домалайтын шариктің траекториялары 1. 2. 4, б-суреттегі «төмпешік моделінде» бейне-ленген. Әрбір рет шарикке бірдей энергия бе-ріледі, бірақ «нысана қашықтық» әртүрлі. «Ны-сана қашықтық» неғұрлым кішкентай болған сайын, шариктің
ϕ
ауытқу бұрышы соғұрлым үлкен болатынына назар аударыңыз.
Домалайтын шариктің траекториялары 1. 2. 4, б-суреттегі «төмпешік моделінде» бейне-ленген. Әрбір рет шарикке бірдей энергия бе-ріледі, бірақ «нысана қашықтық» әртүрлі. «Ны-сана қашықтық» неғұрлым кішкентай болған сайын, шариктің
ϕ
ауытқу бұрышы соғұрлым үлкен болатынына назар аударыңыз.
Бірсыпыра
 «нысана қашықтықтар» үшін траекторияларды есептей отырып
«нысана қашықтықтар» үшін траекторияларды есептей отырып
 «нысана қа-шықтықтар» мен соларға сәйкес алынатын
ϕ
ауытқу бұрыштары арасындағы тәуелділік гра-фигін салуға болады. Кулондық тебіліс күші үшін бұл байланыс, яғни
«нысана қа-шықтықтар» мен соларға сәйкес алынатын
ϕ
ауытқу бұрыштары арасындағы тәуелділік гра-фигін салуға болады. Кулондық тебіліс күші үшін бұл байланыс, яғни
 -
дің
ϕ
-
ге
тәуелділік графигі 1. 2. 5-суретте көрестілген.
-
дің
ϕ
-
ге
тәуелділік графигі 1. 2. 5-суретте көрестілген.
RaC шығаратын
α
-бөлшектер үшін
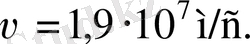 r
0
қашық-тықты алтын (
Z
=79) үшін бағалайық. Ол үшін
r
0
қашық-тықты алтын (
Z
=79) үшін бағалайық. Ол үшін
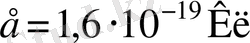 және
және
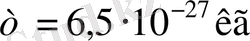 сан мәндерді (1. 2. 1) формулаға қояйық,
сан мәндерді (1. 2. 1) формулаға қояйық,
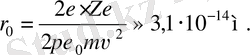
Алтын атомы ядросының өлшемі осы шамадан кіші. Егер элек-трон пішіні сфералық деп жорамалдасақ, онда оның «класси-калық радиусы» осы шамалас болуы керек. Басқа да маңызды пысықтаушы жағдайлар электрондар ядро ішінде бола алмайды деген қорытындыға алып келеді, өйткені ядроның өлшемі 10 −15 м.
α
-бөлшектің
ϕ
бұрышқа ауытқу [
ϕ
бұрыш
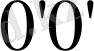 асимптотаның 00 түзумен қиылысуымен анықталады (1. 2. 6-сурет) ] траектория-сы «нысана қашықтыққа» функционалды тәуелді және келесі теңдікпен анықталады (қорытылып шығарылуын келтірмейміз) :
асимптотаның 00 түзумен қиылысуымен анықталады (1. 2. 6-сурет) ] траектория-сы «нысана қашықтыққа» функционалды тәуелді және келесі теңдікпен анықталады (қорытылып шығарылуын келтірмейміз) :
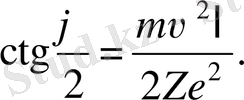 (1. 2. 2)
(1. 2. 2)
(1. 2. 2) өрнекте ϕ шашырау бұрышының шамасына ықпал жасай-тын себепші факторлар көрсетілген (яғни бұл формула болып жатқан оқиғаның физикалық мағынасын ашады) .
 Алтын қаңылтыр арқылы
α
-бөлшектердің параллель шоғы ұшып өтеді делік. Осы бөлшектердің қанша саны
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа ауытқитынын есептейік.
Алтын қаңылтыр арқылы
α
-бөлшектердің параллель шоғы ұшып өтеді делік. Осы бөлшектердің қанша саны
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа ауытқитынын есептейік.
 және
және
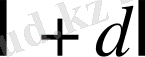 цилиндрлік беттермен шектелген цилиндр қабаттың іші-мен ұшатын
α
-бөлшектер
цилиндрлік беттермен шектелген цилиндр қабаттың іші-мен ұшатын
α
-бөлшектер
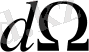 денелік бұрыштың ішінде шашы-райды (1. 2. 6-сурет) . Радиусы
денелік бұрыштың ішінде шашы-райды (1. 2. 6-сурет) . Радиусы
 және
және
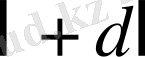 дөңгелектер аралы-ғындағы цилиндрлік қабат қимасының ауданы мынадай:
дөңгелектер аралы-ғындағы цилиндрлік қабат қимасының ауданы мынадай:
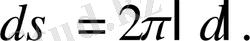 (1. 2. 3)
(1. 2. 3)
Егер заттың 1см
3
көлеміндегі массасы М атомдар саны
п
-
ге
тең, шашырататын қабаттың қалыңдығы
h
-
қа
тең болса, онда көлденең қимасы
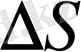 және қалыңдығы
h
болатын
және қалыңдығы
h
болатын
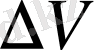 көлемдегі атомдардың жалпы саны мынаған тең:
көлемдегі атомдардың жалпы саны мынаған тең:
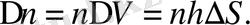 (1. 2. 4)
(1. 2. 4)
Бүкіл осы атомдардың
 нысана қашықтығы (
нысана қашықтығы (
 және
және
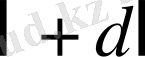 ин-тервалмен) үшін (1. 2. 3) өрнекпен берілетін қиманың жалпы ауданы
ин-тервалмен) үшін (1. 2. 3) өрнекпен берілетін қиманың жалпы ауданы
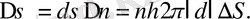 (1. 2. 5)
(1. 2. 5)
Ауданы
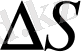 шашыратқыш үлгі (біздің суретте алтын қаңылтыр) бетіне түсетін
α
-бөлшек (1. 2. 2,
а
-сурет)
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа ауытқуының
шашыратқыш үлгі (біздің суретте алтын қаңылтыр) бетіне түсетін
α
-бөлшек (1. 2. 2,
а
-сурет)
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа ауытқуының
 ықтималдығы
ықтималдығы
 ауданның
ауданның
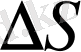 ауданға (үлгінің бүкіл ауданы) қатынасына тең, яғни
ауданға (үлгінің бүкіл ауданы) қатынасына тең, яғни
 (1. 2. 6)
(1. 2. 6)
Егер
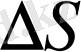 ауданға 1с ішіне
N
α
-бөлшек түссе, онда
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа шашырайтын бөлшектердің ықти-мал саны мынадай болады:
ауданға 1с ішіне
N
α
-бөлшек түссе, онда
ϕ
және
ϕ
+
dϕ
интервалда жататын бұрышқа шашырайтын бөлшектердің ықти-мал саны мынадай болады:
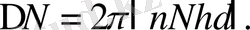 (1. 2. 7)
(1. 2. 7)
 өрнекті табу үшін (1. 2. 2) формуланы пайдаланамыз, сонда
өрнекті табу үшін (1. 2. 2) формуланы пайдаланамыз, сонда
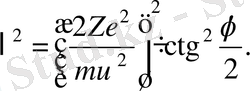
Осы өрнекті дифференциалдасақ мынаны аламыз:
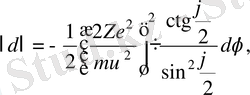 немесе
немесе
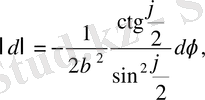 (1. 2. 8)
(1. 2. 8)
мұндағы
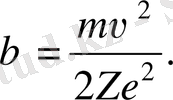
(1. 2. 7) және (1. 2. 8) формулалардан мынаны аламыз:
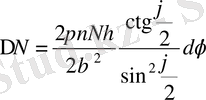 (1. 2. 9)
(1. 2. 9)
(″−″ таңбасы алынып тасталынды, өйткені ол маңызды емес) .
Егер (1. 2. 9) өрнектің оң жағын
 -
ге
көбейтіп, содан соң бөлсек және
-
ге
көбейтіп, содан соң бөлсек және
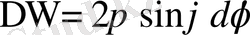 (1. 2. 10)
(1. 2. 10)
денелік бұрышты енгізсек, онда (1. 2. 9) формуланы келесі түрде қайта жазуға болады:
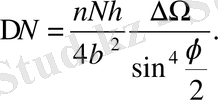 (1. 2. 11)
(1. 2. 11)
(1. 2. 11) қатысқа
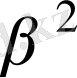 мәнін қойсақ, онда
мәнін қойсақ, онда
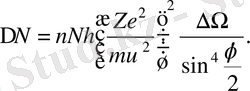 (1. 2. 12)
(1. 2. 12)
Егер экран алтын қаңылтырдың шашырату центрінен R қашық-тықта орналасса, ал ауданның шамасы 1см 2 болса, онда
 (1. 2. 13)
(1. 2. 13)
Сонда (1. 2. 13) шартты қанағаттандыратын
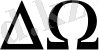 үшін (1. 2. 12) өр-нек мынадай түр алады:
үшін (1. 2. 12) өр-нек мынадай түр алады:
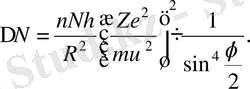 (1. 2. 14)
(1. 2. 14)
(1. 2. 14) өрнек Резерфорд формуласы деп аталады. α -бөлшектер-дің шашырауына жүргізілген тәжірибелер Резерфорд формула-сын толық растады.
Бөлшектер бүкіл бағытқа ауытқитын (шашырайтын) болғандықтан, олар сфера (шар) беті бойымен таралады. Егер берілген
ϕ
бұрыштан артып кететін бұрыштарға ауытқыған (шашыраған) бүкіл бөлшектерді есептесек, онда біз сфера (шар) сегментінің ішіне түсетін (енетін) бөлшектерді есептейміз. 1. 2. 7-суретте
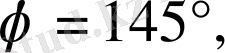 75°, 5° бұрыштар үшін сегменттер көрсетілген.
75°, 5° бұрыштар үшін сегменттер көрсетілген.
 Енді электрондарға келетін болсақ, тепе-теңдік күй үшін олар оң зарядталған ядроның айналасында айналуы қажет (1. 2. 8-сурет), себебі егер электрондар тыныштықта болса, онда кулон-дық тартылыс күштері салдарынан олар ядроға құлауы керек.
Енді электрондарға келетін болсақ, тепе-теңдік күй үшін олар оң зарядталған ядроның айналасында айналуы қажет (1. 2. 8-сурет), себебі егер электрондар тыныштықта болса, онда кулон-дық тартылыс күштері салдарынан олар ядроға құлауы керек.
Сөйтіп, атомның ядролық моделі статикалық модель емес, динамикалық модель және электрондар ядро айналасында қозға-луы керек екендігі белгілі болды. Атом біздің күн жүйемізге ұқсас болып шықты: жүйенің ортасын-да «күн» − ядро жатады, ал оның айналасында ор-бита бойымен «планеталар» − электрондар қозға-лады. Сондықтан Резерфорд моделін планеталық модель деп те атайды. Бірақ бұл алдамшы ұқсас-тық:
1) өзара тартылыс күштерімен байланысқан планеталарға қарама-қайшылығы, электрондардың бір-бірінен тебілетіндігі;
2) ішкі планеталардың тартуы арқасында Күннің сыртқы планеталарға әсер етуі (ықпалы) күшейеді;
3) атомда, керісінше, ядроның сыртқы электрондарға тигізе-тін әсерін ішкі электрондар әлсіретеді − ядроны қалқалайды;
4) планеталардың массалары бірдей емес, ал электрондар-дың массалары мен зарядтары теңбе-тең;
5) атом ерекше орнықтылыққа ие, ал мұндай орнықтылық (тұрақтылық) планета жүйесіне тән емес, денелер қозғалысы ал-дағы болып өткен тарихқа тәуелді (осы негізгі өзгешелік (ұқсас еместік) терең және маңызды) .
Әртүрлі заттың шығаратын сәулесінің спектрлік құрамы түрліше. Бүкіл спектр үш түрге бөлінеді: үзіліссіз (немесе тұ - тас ), жолақ , сызықтық .
Тұтас спектрлерді , тәжірибе көрсететіндей, жоғары темпе-ратураға дейін қыздырылған қатты және сұйық денелер шыға-рады (1. 2. 9, а -сурет) . Тұтас спектр деген атауды алу себебі, мұн-да бүкіл толқын ұзындықтар келтірілген. Бұл спектр ешбір үзі-ліссіз түрлі-түсті тұтас жолақтар түрінде бақыланады.
Жолақ спектрлер қара-қоңыр аралықтармен бөлінген бірсы-пыра жеке жолақтардан тұрады. Айыру қабілеті өте жоғары спектрлік аппаратпен зерттегенде, әрбір жолақ бір-біріне жақын орналасқан сызықтардың өте көп санының жиынтығы болып са-налатыны мәлім болды. Жолақ спектрлер атомдармен емес, бай-ланыспаған молекулалармен немесе бір-бірімен әлсіз байланыс-қан молекулалармен пайда болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz