Лагранж әдісі туралы

Пән: Математика, Геометрия
Жұмыс түрі: Іс-тәжірибеден есеп беру
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Мазмұны

Лагранж әдісі туралы жалпы
Лагранж көбейткіштер әдісі
Анықталмаған Лагранж көбейткіштерінің әдісін қолдану ерекшеліктері

Пайдаланылған әдебиеттер

1. Лагранж әдісі туралы жалпы

Лагранж әдісінде қозғалмайтын санақ жүйесіндегі сұйықтың өзі қарастырылады. Сұйық бөлшек алынады. Бастапқы уақыт мезетіндегі бұл бөлшектің координаты { x ₀ , y ₀ , z ₀ } оны басқа бөлшектерден ерекшелейді; осы координаттарды беру арқылы бұл бөлшекті «белгілеп қоямыз» деуге болады. Онан әрі бөлшек қозғалыс траектория табылады:

x = x ( x ₀ , y ₀ , z ₀ , t ), y = y ( x ₀ , y ₀ , z ₀ , t ), z = z ( x ₀ , y ₀ , z ₀ , t ),

мұндағы х, у, z - анықталатын шамалар; x ₀ , y ₀ , z ₀ , t - Лагранж айнымалары деп аталатын тәуелсіз айнымалар.

Лагранж әдісі жеке бөлшек қозғалыс траекториясын зерттеу қажет болатын жағдайдағы практикалық есептерде колданылады. Бірақ көп жағдайда жеке бөлшек қозғалысы емес, берілген уақыт сәтіндегі барлық бөлшектердің нәтиже қозғалысын зерттеу керек болады. Мысалы, қатты денеге әсер ететін сұйықтың кедергі күші сол денені соғатын өте көп бөлшектердің әсерімен анықталады.

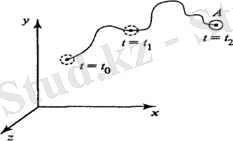
1-сурет. А бөлшегінің әртүрлі уақыт сәтіндегі траекториясы.

Траектория - бойымен қарастырылатын бөлшек қозғалатын кеңістіктегі сызық. Бұл геометриялық үлгі қозғалысты Лагранж әдісімен сипаттауға сәйкес. А бөлшек траекториясы 1-суретте көрсетілген, онда бір ғана А бөлшегінің әртүрлі t ₁ , t ₂ , t ₃ , . . . уақыт сәтіндегі орындары салынған.

Координатасы х, у, z болатын А бөлшегінің t уақыт сәтіндегі жылдамдығы мынаған тең:

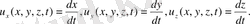
Осыдан:

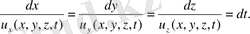(10)

(10) теңдеу - траекторияның дифференциалды теңдеуі.

2. Лагранж көбейткіштер әдісі

Сызықтық емес бағдарламалау есебінің жеке түрі ретінде шектемелері тек теңдеулерден тұратын жағдайын қарастырайық. Ол есепті классикалық тиімді есебі деп атайды:

(4)

(5)

Бұл есепті шешу үшін Лагранж көбейткіщтер әдісін қолдануға болады. Ол бойынша 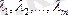деген белгісіз айнымалыларды енгіземіз; олар Лагранж көбейткіштері деп аталады. Осыдан кейін Лагранж функциясы құрастырылады:

(6)

Осы Лагранж функциясының бірінші туындыларын нөлге теңестіру арқылы келесі теңдеулер жүйесін аламыз:

(7)

Бұл теңдеулер жүйесінің кез-келген шешімі F функциясының экстремумын береді.

Сонымен, Лагранж әдісінің шешу жолы былайша жазылады:

1. Лагранж функциясын (6) құрастыру .

2. Лагранж функциясының туындыларын тауып, оларды нөлге теңестіру керек.

3. Осыдан алынған (7) теңдеулер жүйесін шешу.

4. Осы шешімдердегі мақсат функциясының мәндерін тауып, салыстыру арқылы мақсат функциясының максимумын немесе минимумын анықтау.

Енді осы әдіске арналған мысал қарастырайық.

Мысал.

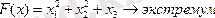
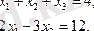
Шешуі:

1. Лагранж функциясын құрастырамыз:

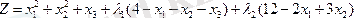
2. Лагранж функциясының туындыларын нөлге

теңестіреміз:

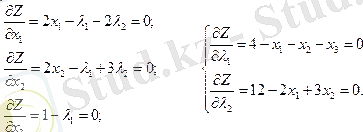
Осы теңдеулер жүйесінің

шешуі:

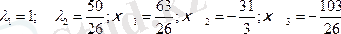
3. Мақсат функциясының осы шешімге сәйкес мәнін табамыз

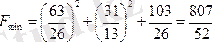
Лагранж бойынша t уақыт - бұл белгіленген бөлшек қозғалысын бақылау уақыты.

Жабық контур арқылы өтетін траекториялардан құралған бетпен шектелген сұйық бөлігі ағым деп аталады (3-сурет) . Ағым ұғымы Лагранж әдісі үшін.

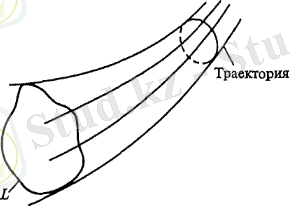
3-сурет. Ағым

Көптеген нақты оптималдандыру есептері бейсызықты болып табылады.

Бейсызықты мақсаттылық функцияның бір немесе бірнеше экстремумі бола алады.

Шартсыз оптималдандыру есептері бейсызықты программалаудың ең қарапайым есептері болып табылады.

Бұл есептерде мақсаттылық функцияның абсолютті экстремумі шектеулерсіз және шектеу шарттарсыз анықталады.

Жоғарғы математика курсынан белгілі, бейсызықты функцияның экстремум нүктесінде (минимум, максимум) оның дербес туындылары нөлге тең болады. Демек, n айнымалысы бар бейсызықты функцияның экстремумін анықтау үшін барлық айнымалылары бойынша дербес туындыларын нөлге теңестіру қажет. n айнымалысы бар n теңдеуден құрылған жүйенің шешімі функцияның экстремумі алынатын айнымалылардың мәндерін береді.

Шартсыз минималдандыру есептері практикада сирек кездеседі, бірақ оларды шешу әдістері шартты оптималдандырудың практикалық есептерін шешудің негізі болып табылады.

Бұл есептерде мақсаттылық функцияның шартты экстремумі анықталады, яғни шектеулер мен шекті шарттарды ескере отырып функцияның экстремумі анықталады.

Шартты оптималдандыру есептерін шартсыз оптималдандыру есептеріне қарағанда шешу қиынырақ.

Сондықтан шартты оптималдандыру есебін (салыстырмалы экстремумін анықтау) қарапайым шартсыз оптималдандыру есебіне келтіруге тырысады (абсолютті экстремумді анықтау) .

Мұндай процедура Лагранж әдісінде орындалады.

Лагранж әдісі.

Бейсызықты функцияның шартты экстремумін анықтау қажет

Z(x ₁ , x ₂ , . . . x _n ) → extr(4. 14)

m шектеулерінде n айнымалыларын анықтау қажет

f ₁ (x ₁ , x ₂ , . . . x _n ) > b ₁ ,

f ₂ (x ₁ , x ₂ , . . . x _n ) = b ₂ , (4. 15)

Лагранж әдісіне сәйкес (4. 16) шектеулерінде (4. 14) функцияның салыстырмалы экстремумінің орнына Лагранж функциясының абсолютті экстремумі анықталады және ол келесі түрде жазылады:

L = Z(x ₁ , x ₂ , . . . x _n ) + λ ₁ f ₁ (x ₁ , x ₂ , . . . x _n , b ₁ ) +λ ₂ f ₂ (x ₁ , x ₂ , . . .

. . . x _n b ₂ ) + . . . + λ _m f _m (x ₁ , x ₂ , . . . x _n , b _m ) → extr, (4. 17)

мұнда λ ₁ , λ ₂ , . . . λ _m - анықталмаған Лагранж көбейткіштері, x ₁ , x ₂ , . . . x _n айнымалылары сияқты ізделетін айнымалылар болып табылады.

Лагранж функциясына мақсаттылық функция және Лагранж көбейткішіне көбейтілген әр шектеу кіретіні байқауға болады.

(4. 16) шектеулерімен (4. 14) мақсаттылық функцияның салыстырмалы экстремумі (4. 17) Лагранж функциясының абсолютті экстремумімен сәйкес келетіні дәлелденген.

(4. 17) функцияның абсолютті экстремумі анықталуы белгілі әдістермен орындалады. Кейбір жағдайда Лагранж функциясының дербес туындылары анықталып, нөлге теңестіріледі:

∂L/∂x ₁ = ∂Z/∂x ₁ + λ ₁ ∂f ₁ /∂x ₁ + λ ₂ ∂f ₂ /∂x ₁ + . . . +λ _m ∂f _m /∂x ₁ =0,

∂L/∂x ₂ = ∂Z/∂x ₂ + λ ₁ ∂f ₁ /∂x ₂ + λ ₂ ∂f ₂ /∂x ₂ + . . . +λ _m ∂f _m /∂x ₂ =0,

. .

∂L/∂x _n = ∂Z/∂x _n +λ ₁ ∂f ₁ /∂x _n + λ ₂ ∂f ₂ /∂x _n + . . . +λ _m ∂f _m /∂x _n =0, (4. 18)

∂L/∂λ ₁ = f ₁ (x ₁ , x ₂ , . . . x _n , b ₁ ) = 0,

∂L/∂λ ₂ = f ₂ (x ₁ , x ₂ , . . . x _n , b ₂ ) = 0,

.

∂L/∂λ _m = f _m (x ₁ , x ₂ , . . . x _n , b _m ) = 0.

Соңғы m теңдеулер оптималдандыру есебінің (4. 16) шектеулерін көрсетеді.

(4. 18) жүйесі (m+n) теңдеуден тұрады және белгісіздер саны да осындай болады. (4. 18) жүйесінің