Сандарды бір санау жүйесінен екінші санау жүйесіне ауыстыру

Кіріспе ... ... ... ... ... ... ... ... ...3
Негізгі бөлім
1. Сандардың тарихы және санау жүйелері ... ... ...4.5
1.1 Санау жүйесі және санау жүйесінің түрлері ... ... 6.9
1.2 Сандарды бір санау жүйесінен екінші жүйесіне ауыстыру ... ... ... ... ...10.13
2 Санау жүйесі ортасында арифметикалық амалдар қолдану ... ... ... ... ... 14.17
2.1 Есептердің әр түрлі жүйеде шығару жолдары..18.19
Қорытынды ... ... ... ... ... ...20
Пайдаланылған әдебиеттер.

50-ші жылдардағы математиктер мен есептеуіш машиналарын құрастырушылардың алдындағы өзекті мәселе қолданбалы бағдарламалау және жаңа есептеу құрылғыларын, шығарушылардың талаптарына сай келетін санау жүйелерін табу болды. Белсенді іздену нәтижесінде санау жүйелеріне және есептеу тәсілдеріне деген көзқарас қысқа мерзімде өзгерді.
Ежелгі интеллектуалдық шеберліктің бірі – арифметикалық санаудың біздің заманымызда да дамуы мүмкін екен.
Математиктердің осы саласының жетістіктері және даму тарихымен танысу – мұғалім үшін маңызды, себебі қазіргі қолданылып жүрген арифметикалық санау жүйесі барлық есептеу математикасының негізі болып саналады.
Курстық жұмысымның тақырыбы «Сандарды бір санау жүйесінен екінші санау жүйесіне ауыстыру». Санау жүйесі әдістерін пайдалана отырып, әртүрлі есептер шығаруға мүмкіндік бар. Санау жүйесі әдістерін қолданып, есептерді бір санау жүйесінен басқа санау жүйелеріне ауыстыруға болады. Сонымен қатар, әртүрлі жүйелердегі сандарға арифметикалық амалдар қолданып есептер шығаруға болады.
Курстық жұмысымның мақсаты қолданушыға санау жүйесі тақырыбында есептер шығару әдістері мүмкіндіктерін ашып көрсету.

1. Е.К.Балапанов, Б.Бөрібаев, А.Дəулетқұлов
«Информатикадан 30 сабақ» Алматы, 1999
2. «Информатика негіздері» журналы 2007ж.
3. Информатика, практикум по технологии работы на компьютере под
ред. проф. Н.В.Макаровой, 1997, Финансы и статистика
4. Специальная информатика С.Симонович, Г.Евсеев, А.Алексеев
Москва, АСТ пресс 2001

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Жоспары

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
Негізгі бөлім
1. Сандардың тарихы және санау жүйелері ... ... ... ... ... ... ... ... ... ... ... ... ... ..4-5
1.1 Санау жүйесі және санау жүйесінің түрлері ... ... ... ... ... ... ... ... ... ... ... ..6-9
1.2 Сандарды бір санау жүйесінен екінші жүйесіне ауыстыру ... ... ... ... ...10-13
2 Санау жүйесі ортасында арифметикалық амалдар қолдану ... ... ... ... ... 14-17
2.1 Есептердің әр түрлі жүйеде шығару жолдары ... ... ... ... ... ... ... ... ... ..18-19
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..20
Пайдаланылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... 21

Кіріспе

50-ші жылдардағы математиктер мен есептеуіш машиналарын құрастырушылардың алдындағы өзекті мәселе қолданбалы бағдарламалау және жаңа есептеу құрылғыларын, шығарушылардың талаптарына сай келетін санау жүйелерін табу болды. Белсенді іздену нәтижесінде санау жүйелеріне және есептеу тәсілдеріне деген көзқарас қысқа мерзімде өзгерді.
Ежелгі интеллектуалдық шеберліктің бірі - арифметикалық санаудың біздің заманымызда да дамуы мүмкін екен.
Математиктердің осы саласының жетістіктері және даму тарихымен танысу - мұғалім үшін маңызды, себебі қазіргі қолданылып жүрген арифметикалық санау жүйесі барлық есептеу математикасының негізі болып саналады.
Курстық жұмысымның тақырыбы Сандарды бір санау жүйесінен екінші санау жүйесіне ауыстыру. Санау жүйесі әдістерін пайдалана отырып, әртүрлі есептер шығаруға мүмкіндік бар. Санау жүйесі әдістерін қолданып, есептерді бір санау жүйесінен басқа санау жүйелеріне ауыстыруға болады. Сонымен қатар, әртүрлі жүйелердегі сандарға арифметикалық амалдар қолданып есептер шығаруға болады.
Курстық жұмысымның мақсаты қолданушыға санау жүйесі тақырыбында есептер шығару әдістері мүмкіндіктерін ашып көрсету.

Сандардың тарихы және санау жүйелері

Ерте замандарда адамдарға өздерінің күнделікті өмірінде кездесіп отыратын әртүрлі нәрселерді санауға тура келген. Сонда адамның тек екіге дейін ғана санай білетін шағы болған. Екі саны адамның көру және есту мүшелерімен, жалпы алғанда нәрселердің нақтылы жұбымен байланыстырылған. Үнділердің көз, тибеттіктердің қанат деген өздері 2 санын білдіретін болған. Егер заттар саны 2-ден артық болса, алғашқы қауым адамы олар туралы тек көп дейтін болған. Адам бірте - бірте ғана үшке дейін, одан кейін беске, онға дейін т.с.с. санап үйренген.
Біздің он - оннан санауымыз бойынша он бірліктен бір ондық, он ондықтан бір жүздік, т.с.с құралады. Осындай он - оннан топтап санау тәсілін ондық санау жүйесі деп атайды.
Балалар саусақтарын санап үйренетіні сияқты, адамдар да қоғам дамуының алғашқы кезеңдерінде санау үшін екі қолының он саусағын пайдаланған. Қазіргі күні де саусақпен санағандай... деп айтамыз. Осыдан ондық санау жүйесі шыққан.
Басқа жерлерде, мысалы, Африкадағы тайпалар мен халықтар санағанда бір қолының бес саусағын ғана пайдаланған, олар бес - бестен санаған, оларда негізі бес саны болатын бестік санау жүйесі қалыптасқан. Бұл санау жүйесінде алғашқы бес санның ғана атаулары бар. Олар алты санын бес - бір деп атаған. Осы санау жүйесінің жұрнақтары Скандинавия халықтарының тілдерінде сақталған.
Ең көне санау жүйесі - екілік санау жүйесі, ғалымдардың болжауы бойынша, бұл жүйені бір кездері мысырлықтар пайдаланған. Екілік санау жүйесінде небары сандық екі таңба ған бар, ол 1 мен 0 цифрлары. Бұл жүйенің артықшылығы - есептеулердің жеңіл орындалуы болса, кемшілігі - сандардың жазылуының шұбыраңқылығы қолайсыз. Қазіргі жылдам есептейтін электронды машиналар жасауға екілік санау жүйесі пайдаланылады.
Жиырмалық санау жүйесінің жұрнақтары осы уақытқа дейін, қазіргі француз және грузин тілдерінде сақталып қалған: ол тілдерде 80 санынының орнына төрт жиырма делінеді. Бұл санау жүйесін қолданған халықтар санағанда қолдарының саусақтарын да, аяқтарының башайларына дейін пайдаланған. Бұл жүйемен Майя тайпасының индеецтері де пайдаланған.
Ежелгі вавилондықтар алпыстық санау жүйесін пайдаланған. Бұл санау жүйесі - дүние жүзіндегі 1-ші позициялық санау жүйесі. Көп уақытқа дейін, ҮІІ ғасырға дейін ғылымда пайдаланылып келді, оның ізі әлі де сақталған.
Қазіргі уақытта дүние жүзінің барлық халықтары дерлік ондық санау жүйесін пайдаланады. Ондық санау жүйесінде 999 миллионға дейінгі барлық натурал сандарды атау үшін тек 13 сөз ғана қолданылады: бір, екі, үш, төрт, бес, алты, жеті, сегіз, тоғыз, он, жүз, мың, миллион.
Жылдам есептеу машиналарында екілік санау жүйесі қолданылуымен байланысты, қазіргі уақытта ондық санау жүйесімен қатар екілік санау жүйесі де практика жүзінде кеңінен қолданылып жүр.
Қандай үлкен санды болсын небәрі он цифр арқылы жазып көрсетуге болады. Цифрларды да, арифметика ережелері сияқты, ешкім бірден ойлап шығарған не тапқан емес. Осы заманғы цифрлар сан ғасырлар бойы қалыптасып жасалған. Цифрлардың сызба таңбалары жазудың дамуымен қатар жетіліп кемелдене берген. Әуелде әріптер болмаған. Адам ойын, сөзін жартастардың, үңгір қабырғаларының, тастардың беттеріне салған суреттері арқылы білдірген. Сандарды есте сақтау үшін адам ағаштарға, таяқтарға кертіп белгі салуды және жіптерге түйіндер салуды қолданған. Мұнан кейін бір санын бір сызықшамен, екі санын екі сызықшамен, үш санын үш сызықшамен, т.с.с. белгілеудің келіп шығуы табиғи нәрсе. Мұндай цифрлардың жұрнақтары, мысалы, римдік санау жүйесінде бар: І, ІІ, ІІІ. Алайда өндіріс пен мәдениет өркендеп, үлкен сандарды жазып көрсету керек болғанда сызықшаларды қолдану қолайсыз болған. Сонда жеке сандарды жазып көрсету үшін ерекше таңбалар қолданылған. Әрбір сөз секілді, әрбір сан да ерекше таңбамен, иероглифпен белгіленген. Мысалы, мұны қытайдың иероглиф цифрларынан көруге болады.
Ежелгі Мысырда бұдан 4000 жылдай бұрын сандарды белгілеу үшін басқа таңбалар мен иероглифтер қолданылған. Бірлік қазықпен, ондық қос қол тәрізденіп белгіленген, жүздік бүктелген пальма жапырағымен, мың молшылық символы ретіндегі лотос гүлімен, жүз мың бақамен белгіленген, өйткені Ніл тасығанда бақалар көбейетін болған.

0.1. Санау жүйесі және санау жүйесінің түрлері

Сандарды цифр деп аталатын арнайы символдардың көмегімен бейнелеу қабылданған. Сандарды атау және жазу ережелері мен әдістерінің жинағын - санау жүйесі деп аталады.
Санау жүйелері екі топқа бөлінеді: позициялық және позициялық емес.
Позициялық емес санау жүйесінде санның әрбір цифрының мәні оның алатын орнына байланысты емес. Мұндай санау жүйесінің мысалы ретінде римдік жүйені алуға болады. Бұл жүйеде жазылған XXX санына X цифры кез кез келген позицияда 10-ды (онды) білдіреді.
Позициялық емес санау жүйесінде арифметикалық амалдарды орындау едәуір күрделі болғандықтан, бүкіл дүние жүзі біртіндеп позициялық санау жүйесіне ауысты.
Позициялық санау жүйесінде цифрдің мәні оның орнына (позициясына) тәуелді. Мысалы, 737,7 санындағы бірінші тұрған 7 жүздікті, екіншісі - 7 бірлікті, ал үшіншісі - бірліктің 7 ондық үлесін білдіреді. Кез келген позициялық санау жүйесі өзінің негізімен сипатталады.
Позициялық санау жүйесінің негізі деп онда қолданылатын цифрлар санын айтады.
Жүйенің негізі ретінде екі, үш, төрт, т.с.с кез келген натурал санды алуға болады. Демек, позициялық жүйенің сансыз көп болуы мүмкін: екілік, үштік, төрттік, т.с.с.
Негізі q санау жүйелерінің әрқайсысында сандардың жазылуы
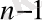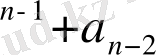aqq
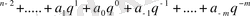
өрнегінің қысқартылған жазылуын білдіреді, мұнда a - cанау жүйесінің цифрлары; n мен m - сәйкес бүтін және бөлшек разрядтардың саны.

Ондық санау жүйесі
Мектеп қабырғасында сандармен жұмыс істегенде, біз бір ғана ондық санау жүйесін қолдануға дағдыландық. Ондық аты бұл жүйенің негізінде он негізгі жатқандығымен түсіндіріледі. Бұл жүйеде сандарды жазу үшін он цифр қолданылады - 0,1,2,3,4,5,6,7,8,9.
Адамдар ондық жүйені ыңғайлы көреді, шамасы, олар санауды алғашқыда саусақпен санап үйренгендіктерінен болар, ал аяқ пен қолдағы саусақтар саны оннан. Бірақ адамдар ондық санау жүйесін әрқашан және барлық жерде қолданбайды. Мысалы, Қытайда ұзақ уақыт бойы бестік санау жүйесін қолданған.
Ондық жүйе позициялық болып табылады, өйткені ондық санның жазылуында цифрдың мәні оның позициясына немесе сандағы орнына байланысты. Санның цифрына бөлінетін позицияны разряд деп атайды.
Мысалы, 425 санының жазуы санның 4 жүздіктен, 2 ондықтан және 5 бірліктен тұратынын білдіреді. Егер осы цифрларды басқа ретте жазатын болсақ, мысалы, 524, онда сан 5 жүздіктен, 2 ондықтан, және 4 бірліктен тұрады. Мұнда 5 цифырының саплмағы ең үлкен болады да, санның үлкен цифры деп аталады, ал 4 цифры - кіші салмақты және осы санның кіші цифры деп атайды. Егер 524 санын қосынды түрінде жазсақ,
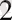5*10+2*10+4*10
Осы жазбадан цифрлар салмағының айырмашылығы айқын көрінеді, бұл жазбадағы 10 саны- санау жүйесінің негізі. Санның әрбір цифры үшін, 10 негізі цифрдың сандағы орнына байланысты дәрежеленеді де, осы санға көбейтіледі. Брліктер үшін негіз1дің дәреже көрсеткіші нөлге, ондықтар үшін - бірге, жүздіктер үшін - екіге тең және т.с.с.
Егер ондық сан бөлшек болса, онда ол да қосынды түрінде оңай жазылады. Онда бөлшек бөліктің әрбір цифры үшін негіздің дәреже көрсеткіші теріс және бөлшек бөліктің үлкен цифры үшін - 1-ге, бөлшек бөліктің келесі цифры үшін - 2-ге тең және т.с.с. болады. Мысалы, келесі ондық сандар мынадай қосындымен көрсетіледі:
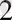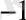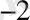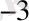384,9506=3*10+8*10+4*10+9*10+5*10+0 *10+6*10

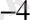
Екілік санау жүйесі.
Компьютерде, әдетте ондық емес, позициялық екілік санау жүйесі, яғни негізгі 2 санау жүйесі қолданылады.
Екілік жүйе кез келген сан 0 мен 1 цифрларының көмегімен жазылады да, екілік сан деп аталады.
Екілік санды тек 0 мен 1 цифрларынан тұратын ондық саннан ажырату үшін, екілік санның жазбасының индексіне екілік санау жүйесінің белгісі тіркеледі, мысалы, 110101,111
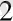
Екілік санның әрбір разрядын (цифрын) бит деп атайды.
Екілік санау жүйесінің маңызды құндылығы - цифрларды физикалық кескіндеудің ыңғайлылығы (мысалы, 1 цифрына электр кернеуінің бар болуы, ал 0 цифрына электр кернеуінің жоқ болуы сәйкес келуі мүмкін) және компьютер құрылғысының, атап айтқанда екілік сандармен арифметикалық және логикалық операцияларды орындауға арналған арифметикалық-логикалық құрылғысының қарапайымдылығы.
Ондық сандар сияқты, кез келген санды оның құрамына кіретін цифрлардың салмағының айырмашылығын анық бейнелейтін қосынды түрінде жазуға болады. Бұл қосындыда негіз ретінде 2 саны қолданылады. Мысалы, 1010101,101 екілік саны үшін қосынды мына түрде болады.

Бұл қосынды ондық санға арналған қосынды ережесі бойынша жазылады. Берілген мысалды екілік сан жеті орынды бүтін және үш орынды бөлшек бөліктерден тұрады. Сондықтан бүтін бөліктің үлкен цифры, яғни бір 2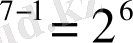-ге көбейтіледі, бүтін бөліктің нөлге тең келесі саны 2 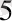көбейтіледі және т.с.с., екінің дәрежелерінің кемуі бойынша бөлшек бөліктің кіші, 2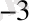-ге көбейтілетін үшінші цифрына дейін болады. Бұл қосындыда арифметикалық операцияларды ондық жүйенің ережелері бойынша орындай отырып, 85,625 ондық санын аламыз. Сонымен, 1010101 екілік саны 85,625 ондық санына сәйкес немесе 1010101,101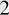=85,625.
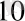Ауыстыру ережесі. Санды екілік жүйеден ондық санау жүйесіне ауыстыру үшін, екілік санды коэффицент - цифрлармен екінің дәрежелерінің көбейтінділерінің қосындысы түрінде жазып, осы қосындыны табу керек.
Екілік жүйенің елеулі кемшілігі - санды бұл жүйеде жазу үшін 0 мен 1 цифрлары мейлінше көп қажет болатындығында. Бұл адамның екілік сандарды қабылдауын қиындатады. Мысалы, 156 ондық санының екілік жүйедегі түрі мынадай: 10011100. Сондықтан екілік жүйені, қағида бойынша компьютердің ішкі қажеттілігі үшін қолданады, ал адамның компьютермен жұмыс істеуі үшін, ұлкен негізді санау жүйесін таңдайды. Бұл жағдайда сегіздік және оналтылық санау жүйелері жиі қолданылады, өйткені бұдан былай көрсетілетіндей, бұл екі жүйе мен екілік жүйенің арасында сандарды бір жүйеден екінші жүйеге ауыстырудлы жеңілдететін қарапайым байланыс бар.
Сегіздік санау жүйесі
Сегіздік санау жүйесінде, яғни негізгі 8 санау жүйесінде сандар сегіз цифрдың көмегімен көрсетіледі. 0,1,2,3,4,5,6,7. Мысалы, 357 санында жеті бірлік, бес сегіз және квадратталған (екі есе) үшсегіз бар, яғни 357 ═3*8²+5*8¹+7*8º, мұндағы 357 санының индексі санау жүйесін білдіреді. Жазылған қосындыда арифметикалық амалдарды ондық жүйенің ережелері бойынша орындай отырып, 357═ 239 екенін аламыз, яғни 357 сегіздік саны 239 ондық санына сәйкес.
Ондық сандарды екілік санау жүйесіне және керсінше түрлендіруді машина орындайды. Компьютерді толық пайдалану үшін машина сөздерін түсіне білу керек. Міне осы мақсатта сегіздік және оналтылық жүйелер қолданылады. Бұл жүйелердегі сандар ондық сандарға ұқсас, ал екілік жүйеге қарағанда үш (сегіздік) және төрт (он алтылық) есе аз разрядтар санын қажет етеді, өйткені 8 және 16 - екінің үшінші және төртінші дәрежелері.

10-дық
2-лік
8-дік
16-лық
10-дық
2-лік
8-дік
16-лық
0
0
0
0
10
1010
12
А
1
1
1
1
11
1011
13
В
2
10
2
2
12
1100
14
С
3
11
3
3
13
1101
15
D
4
100
4
4
14
1110
16
E
5
101
5
5
15
1111
17
F
6
110
6
6
16
10000
20
10
7
111
7
7
17
10001
21
11
8
1000
10
8
18
10010
22
12
9
1001
11
9
19
10011
23
13

Оналтылық санау жүйесі
Екілік санау жүйесі компьютерден тыс қолдануға қолайсыз екенін біз жоғарыда айтқанбыз. Мысалы, 895128 ═11011010 1000010011000
Екілік сандарды жазуды қысқарту үшін негізгі санау жүйесінқолданады. Бұл жүйені оналтылық деп атайды.
Оналтылық позициялық санау жүйесінде санды жазу үшін ондық санау жүйесінің цифрлары 0,1,2,3,4,5,6,7,8,9 және жетпейтін алты цифрды белгілеу үшін 10,11,12,13,14 және 15 ондық сандарының мәніне сәйкс латын алфавитінің алғашқы үлкен әріптері: A, B, C, D, E, F қолданылады. Сонымен ондық жүйенің барлық цифрлары және бұдан басқа алты латын әріпі оналтылық санау жүйесінің цифрлары болып табылады.
Оналтылық санау жүйесінің барлық цифрларын келтірейік: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Оналтылық санау жүйесінде F санынан кейін ондық жүйеде 15+1=16 дегенге сәйкес F+1 саны келеді.
Сондықтан оналтылық сан, мысалы, мына 3E5A1 түрде болуы мүмкін. Бұл санды негізі 16 екенін ескертіп, қосынды түрінде жазсақ:

.
А=10, Е=14 екенін ескертіп, теңдігін аламыз.

0.2. Сандарды бір санау ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.