C[0,1], L^p және Гильберт кеңістіктеріндегі сызықтық функционалдардың Рисс теоремелері


Кіріспе
Алдыңғы тарауларда ақырлы өлшемді Евклид кеңістігінде және Гильберт кеңістігінде анықталган функционалдардың жалпы түрі анықталды. Бұл тарауда осы мәселе басқа да негізгі кеңістіктерде шешіледі. Функциялар кеңістігі [0, 1] кесіндісінде қарастырылады, бірақ дәлелденген теоремалар кез-келген
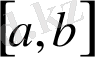 кесіндісі үшін сақталады. Функционалдың жалпы түрі анықталған кеңістіктің түйіндес кеңістігі айқындалады.
кесіндісі үшін сақталады. Функционалдың жалпы түрі анықталған кеңістіктің түйіндес кеңістігі айқындалады.
Фридьеш Рис (венг. Frigyes Riesz , 22 января 1880 - 28 февраля 1956) - венгрлік математик, қазіргі функционалдық талдаудың негізін құрушы. Математик Марсель Ристің ағасы.
Фридьеш Рис Дьёреде (Австро-Венгрия) европалық отбасында дүниеге келді. Оның әкесі -Играц Рис -дәрігер болған. Фридьеш Рис Будапеште, Гёттингенде және Цюрихте оқыған, 1902 жылы Будапештте геометриядан докторлық десертацисын қорғады. Университетте жұмыс істегеннен бұрын мектепте мұғалім болып жұмыс істеген.
1907-1909 жылдары Рис функцияларды зерттеуге байланысты жұмыстарын жариялады.
1911 жылы Рис Коложвар университетінде кафедра меңгерушісі болып тағайындалды.
1945 жылы Рис Будапешт университетінің математика кафедрасына жұмысқа қабылданды.
Рис Венгрияның ғылым Академиясының мүшесі болды.
Эрнст Фишер неміс математигі. Кельнда профессор болды. Емми және Макс Нетер мен бірге жұмыс жасады. Негізгі еңбектері функция теориясымен функционалдық талдауға байланысты.
1 НЕГІЗГІ КЕҢІСТІКТЕРДЕГІ СЫЗЫҚТЫҚ ФУНКЦИОНАЛДАР
1. 1 Рисс теоремасы
Теорема ( Рисс ) . Н -Гильберт кеңістігінде { e k } ортонормал жүйе және
шартты қанағаттандыратын с k - сандар тізбегі берілген болсын.
Онда Н кеңістігіне тиісті х элементі табылып: с k -лар х элементінің Фурье коэффициенттері, яғни
және
болады.
Енді Гильберт кеңістігінің кейбір ішкі кеңістіктерін қарастырамыз.
Гильберт кеңістігі нормаланған кеңістік болғандықтан, оның ішкі кеңістіктерін нормаланған кеңістіктердегі сияқты анықтаймыз.
Демек, Н тің ішкі кеңістігі - тұйық болған сызықтық кеңістіктер.
1. 2 С[0, 1] кеңістігіндегі сызықтық функционалдың жалпы түрі
Теорема (Ф. Рисс) . С[0, 1] кеңістігіндегі кез келген сызықтық, функционал
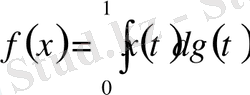
теңдігі түрінде Стильтьес интегралы арқылы өрнектеледі. Мұндағы
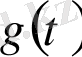 функциясы
функциясы
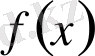 функционалы арқылы анықталатын өзгеруі шенелген функция және
функционалы арқылы анықталатын өзгеруі шенелген функция және
 .
.
Дәлелдеуі. Интегралдың сызықтық қасиетінен (1) формуласы кез-келген өзгеруі шенелген
функциясы арқылы С[0, 1] кеңістігінде сызықтық функционалды анықтайтыны айқын. С[0, 1] кеңістігіндегі жинактылық бірқалыпты болғандықтан, Стильтьес интегралының ішінде шекке көшуге болады, демек,
) үздіксіз функционал. Осымен кез-келген өзгеруі шенелген функцияға сәйкес, С[0, 1] кеңістігінде анықталған, шенелген
функционалы бар екендігі айқындалды. Енді әрбір осындай функционалға сәйкес өзгеруі шенелген функция бар екенін дәлелдейік.
С[0, 1] кеңістігінде анықталған кез-келген
функционалы берілген болсын. С[0, 1] кеңістігі М[0, 1] кеңістігінің ішкеңістігі екені мәлім (І. 2. ) . Банах-Хан теоремасы бойынша
функционалын М[0, 1] кеңістігіне нормасын сақтай кеңейтуге болады. М[0, 1] кеңістігіне кеңейтілген функционал Ғ(х) болсын. Сонда, егер
болса, онда
және
. Енді
квадратында
функциясын анықтайық: егер
болса, онда
, ал
болса, онда
болсын. Әрбір тиянакты
үшін,
айнымалысынашһ тәуелді функция ретінде,
екені айқын. Сондықтан
, яғни
-ға тәуелді функция болады. Осының өзгеруі шенелген функция екенін дәлелдейік.
[0, 1] кесіндісін
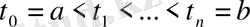 нүктелері арқылы бөліктерге бөлейік. Кез-келген нақты
нүктелері арқылы бөліктерге бөлейік. Кез-келген нақты
 саны үшін
саны үшін
 екенін және Ғ сызықтық функционал екенін ескере отырып, мына қосындыны бағалайық (мұндағы
екенін және Ғ сызықтық функционал екенін ескере отырып, мына қосындыны бағалайық (мұндағы
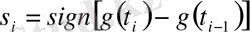 ) :
) :
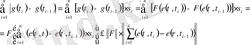 (2)
(2)
Соңғы қосындының нормасы 1-ге тең, себебі,
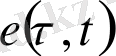 функциясының анықталуы бойынша, егер
функциясының анықталуы бойынша, егер
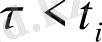 , болса, онда
, болса, онда
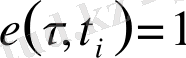 , ал
, ал
 , болса, онда
, болса, онда
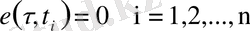 . Сондықтан
. Сондықтан
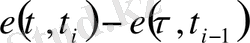 айырмасы
айырмасы
 аралығында 1-ге, қалған нүктелерде 0-ге тең. Онан кейін
аралығында 1-ге, қалған нүктелерде 0-ге тең. Онан кейін
 екенін ескерсек, онда (2) теңсіздігінен
екенін ескерсек, онда (2) теңсіздігінен
 (3)
(3)
теңсіздігі шығады. Өзгеруі шенелген функцияның анықтамасы бойынша (3) теңсіздігінен
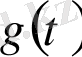 функциясы [0, 1] кесіндісінде өзгеруі шенелген функция деген қорытынды шығады.
функциясы [0, 1] кесіндісінде өзгеруі шенелген функция деген қорытынды шығады.
Енді кез-келген
 функциясын алып, жоғарыда қарастырылған
функциясын алып, жоғарыда қарастырылған
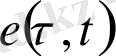 функциясын пайдаланып, мына функцияны құрайық:
функциясын пайдаланып, мына функцияны құрайық:
 (4)
(4)
(3) теңсіздігінің алдында
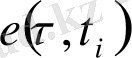 функциясы туралы айтылған қорытындыдан (4) функциясы баспалдақты функция екенін, дәлірек айтқанда, әрбір
функциясы туралы айтылған қорытындыдан (4) функциясы баспалдақты функция екенін, дәлірек айтқанда, әрбір
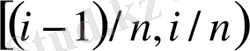 бөлік аралықта оның мәні тұрақты
бөлік аралықта оның мәні тұрақты
 санына тең болатынын аңғарамыз. Ғ функционалының осы функциядағы мәні
санына тең болатынын аңғарамыз. Ғ функционалының осы функциядағы мәні
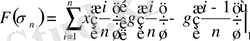 (5)
(5)
Бұл теңдіктің оң жағы
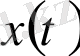 функциясының
функциясының
 функциясы бойынша интегралдық қосындысы. Бөліктеуді шексіз ұсақтағанда бұл қосындының шегі
функциясы бойынша интегралдық қосындысы. Бөліктеуді шексіз ұсақтағанда бұл қосындының шегі
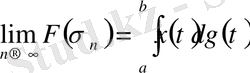 (6)
(6)
Стильтьес интегралына тең.
Екінші жағынан,
функцияларының тізбегі [0, 1] кеңістігінде
функциясына бірқалыпты жинақталады. Шынында да, кез-келген
нүктесі бөлік аралықтардың бірінде жатады, яғни
қандай натурал сан болса да
болатындай
нөмірлі бөлік аралық табылады. Сондықтан
,
Демек,
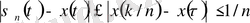 (7)
(7)
Соңғы (7) теңдігі кез-келген
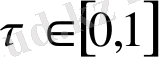 үшін орындалады (
үшін орындалады (
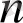 нөмірі
нөмірі
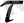 -ға тәуелсіз), демек,
-ға тәуелсіз), демек,
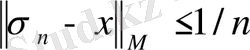 ,
,
яғни М кеңістігінде
тізбегі
функциясына жинақталады. Ал
осы кеңістікте анықталған үздіксіз функционал болғандықтан
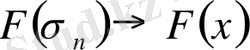
Енді (5), (6), (8) арақатынастарынан

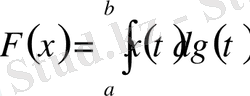 (9)
(9)
теңдігі шығады, ал
 , демек,
, демек,
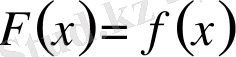 екенін еске алсақ, онда (9) теңдігі (1) теңдігімен пара-пар екені көрінеді.
екенін еске алсақ, онда (9) теңдігі (1) теңдігімен пара-пар екені көрінеді.
Теореманы аяқтау үшін
 функционалының нормасын табу керек. (3) теңсіздігінен
функционалының нормасын табу керек. (3) теңсіздігінен
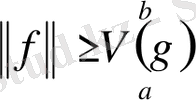 теңсіздігі шығады. Қарама- қарсы теңсіздікті дәлелдеу үшін (1) теңдігін бағалайық:
теңсіздігі шығады. Қарама- қарсы теңсіздікті дәлелдеу үшін (1) теңдігін бағалайық:
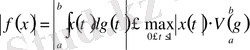
демек,
 , яғни функционалдың нормасы функциясының кесіндісіндегі өзгеруіне тең екендігі дәлелденді.
, яғни функционалдың нормасы функциясының кесіндісіндегі өзгеруіне тең екендігі дәлелденді.
2.
кеңістігіндегі сызықтық функционалдың жалпы түрі
Теорема.
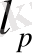 (р>1) кеңістігінде анықталған шенелген сызықтық функционал
(р>1) кеңістігінде анықталған шенелген сызықтық функционал
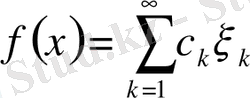
түрінде болады. Мұнда
. Функционалдың нормасы
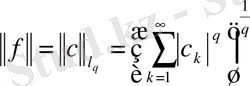 (2)
(2)
Дәлелдеуі. Кез-келген
 элементі бойынша (1) теңдігі
элементі бойынша (1) теңдігі
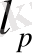 кеңістігінде шенелген сызықтық функционал анықтайтынын тексерейік. Қатарлар үшін Минковский теңсіздігінен (I. 2. (24) ), егер
кеңістігінде шенелген сызықтық функционал анықтайтынын тексерейік. Қатарлар үшін Минковский теңсіздігінен (I. 2. (24) ), егер
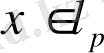 және
және
 болса, онда бұлардың сызықтық комбинациясы
болса, онда бұлардың сызықтық комбинациясы
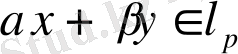 екені шығады. Осыдан, жэне функционалды анықтайтын (1) тендігінен,
екені шығады. Осыдан, жэне функционалды анықтайтын (1) тендігінен,
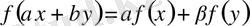
теңдігі тікелей шығады. Оның шенелгендігін тексеру үшін Гельдер теңсіздігін (I. 2. (23) ) қолданайық:
 (3)
(3)
яғни,

Енді
 кез-келген,
кез-келген,
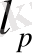 кеңістігінде анықталған, шенелген функционал болсын. Осы кеңістіктегі
кеңістігінде анықталған, шенелген функционал болсын. Осы кеңістіктегі
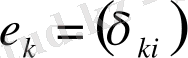 элементтері базис болғандықтан, кез-келген
элементтері базис болғандықтан, кез-келген
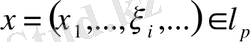 элементтер бойынша жіктеледі:
элементтер бойынша жіктеледі:
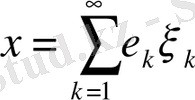 (4)
(4)
Функционалдың сызықтық қасиеті бойынша
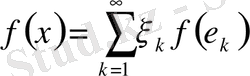
демек, (1) теңдігіндегі коэффициенттер
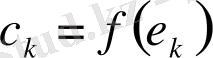 түрінде бірмәнді анықталады.
түрінде бірмәнді анықталады.
Вектор
екенін дәлелдейік. Осы мақсатпен әрбір
үшін
, векторын қарастырайық. Мұндағы
. Функционалдың осы вектордағы мәні
 (5)
(5)
Сонымен қатар,
 (6)
(6)
Соңғы (5), (6) арақатынастарын салыстыра отырып және
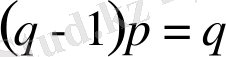 екенін ескеріп,
екенін ескеріп,

Теңсіздігін, ал мұнан
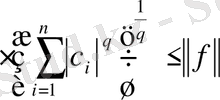 (7)
(7)
Теңсіздігін аламыз. Бұл теңсіздік кез-келген
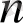 үшін орындалады, демек,
үшін орындалады, демек,
 кезде, осыдан
кезде, осыдан
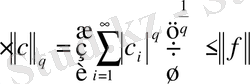
теңсіздігі шығады, ал бұл
екенін көрсетеді. Акырында, (3), (7) теңсіздіктерінен нормалардың теңдігі шығады:
. Теорема дәлелденді.
Салдар.
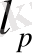 кеңістігіне түйіндес кеңістік
кеңістігіне түйіндес кеңістік
 ,
,
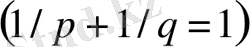
3.
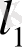 және с
0
кеңістіктері
және с
0
кеңістіктері
Өткен пункттегі теорема параметр
жағдайында дәлелденді. Ал
кеңістігі
мәні үшін де анықталған. Бірақ
болса, онда
ақырлы сан емес (
) . Сондыктан дәлелденген теорема бұл жағдайды қамти алмайды, демек
кеңістігіне түйіндес кеңістіктің қандай екені әзірше айқын емес. Осыған байланысты мына тұжырымды дәлелдейік.
2. 1 Рис ұсынған теорема
Рис ұсынған теорема (тағы Рис - Фрешье теоремасы) -гильберттік кеңістіктегі әрбір сызықтық шектеулі функционал сколярлы көбейтінді арқылы көрсетілуі мүмкін функционалдық талдаудың қабылдауы. Венгерлік математик Фридьеш Ристің атымен аталған.
Тұжырымдама
Кеңістікте
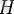 гильберттік кеңістік пен сызықтық шектеулі функционал
гильберттік кеңістік пен сызықтық шектеулі функционал
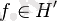 болсын. Онда
болсын. Онда
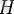 кеңістігінде бір ғана элемент
кеңістігінде бір ғана элемент
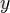 бар, бірақ негізсіз
бар, бірақ негізсіз
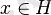
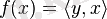 орындалады. Сонымен қоса
орындалады. Сонымен қоса
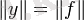 теңдігі орындалады.
теңдігі орындалады.
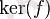 сызықтық функционалдың өзегі векторлы
сызықтық функционалдың өзегі векторлы
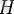 кеңістік.
кеңістік.
Егер
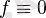 , алу жеткілікті
, алу жеткілікті
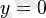 . Егер де
. Егер де
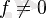 , онда
, онда
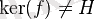 . Тиісінше элементін табуға болады
. Тиісінше элементін табуға болады
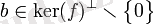 ,
,
 , белгілейік
, белгілейік
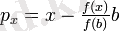 .
.
Өйткені
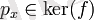 , негіз бойынша
b
болады
, негіз бойынша
b
болады
 . Сызықтықтың скалярлық көбейтіндісінен аламыз:
. Сызықтықтың скалярлық көбейтіндісінен аламыз:

Осы жерден
.
Соңында :
,
бұл жерде
.
2. 2
R толық бөлінетін евклит кеңістігі және φ п азғана мөлшерленген ортогоналды жүйе болсын. Бессельдің теңсіздігінен, егер с 1 . . . , с п . . . , сандары қандайда бір Фурье f∈ R коэфицентінің элементі болуы үшін, қатары
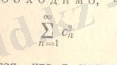
сай келуі керек. Келесі теорема орынды болып келеді.
Теорема 3 (Рисс-Фишер) . φ п - толық евклит кеңістігіндегі R еркін ортогоналді қалыпты жүйе және сандар
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz