Параметрлік иррационал теңдеулер: анықтама, шешу әдістері және мысалдар

ПАРАМЕТРЛІ ИРРАЦИОНАЛ ТЕҢДЕУЛЕР

Иррационал теңдеу - деп белгісіздері рационал таңбасы астында немесе бөлшек дәрежеге шығарған амалдардың таңбасы астында болып келген теңдеулерді айтады. Мұндай теңдеулердің негізгі қасиеттерін еске түсірейік.

Теңдеуге енетін барлық жұп дәрежелі түбірлер арифметикалық түбірлер, яғни түбір астында тұрған өрнектер тек теріс емес мәндер үшін анықталған, ал түбірдің өзі тек теріс емес мәндер ғана қабылдайды.

Теңдеуге енетін барлық тақ дәрежелі түбірлер түбір таңбасы астында тұрған өрнектің кез-келген нақты мәндерінде анықталған, түбір таңбасы астында тұрған өрнектің таңбасына қарай теріс таңбалы емес мәндерді де, теріс таңбалы мәндерді де қабылдай береді.

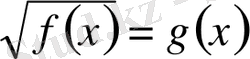теңідеуі мына жүйеге мәндес.

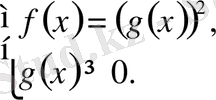
Иррациоиал теңдеуді шешуде қолданылатын негізгі әдістер.

- теңдеудің екі жағын да бірдей белгілі бір дәрежеге шығару;

- белгісізді ауыстыру;

- теңдеудің екі жағын да бірдей белгілі бір функцияға көбейту;

- теңдеуге енетін функцияның қасиетін және олардың графиктерін пайдалану.

Көрсетілген әдістерді қолданып, кейбір түрлендірулер жасағанда, мысалы, теңдеудің екі жағын да бірдей жұп дәрежеге шығарғанда, берілген теңдеудің түбірлерінен басқа, бөгде түбірлердің пайда болатындығын ескертеміз. Сондықтан теңдеуді шығарып болған соң, бөгде түбірлерден құтылу әдістерін қарастыруымыз керек. Әдетте оны тексеру әдісі арқылы жүргізеді. Сондықтан да тексеру иррационал теңдеулерді шешудің бір кезеңі болып табылады.

Кейде иррационал теңдеуді басқа әдіспен - теңдеудің анықталу облысы мен теңдеудің екі жағы теріс емес талапты қанағаттандыратындай етіп, жұп дәрежеге шығарып, берілген теңдеуге мәндес жүйеге көшу арқылы шығарады. Теңдеудің екі жағын да бірдей тақ дәрежеге шығарғанда, берілген теңдеуге мәндес теңдеу шығатындығын тағы да ескертеміз.

Eгep f ( a, b, c, . . . , k. x ) = ( a, b. c, . . . , k, x ) теңдеуінің бір немесе екі (жағы) бөліп х -ке қарағанда иррационал құрамы бар өрнектер болатын болса онда ол бір белгілі х бар иррационал теңдеу деп аталады.

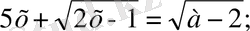
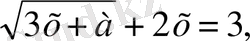
Мысалы, 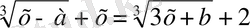теңдеулері х -ке қарағанда иррационал теңдеулер. Бұл арада а және b параметрлер нақты түбірлерді тапқанда екендігіне сүйенеміз. Сонда n - жұп caн болғанда,

f ( a, b, c, . . . , k. x ) ≥ 0. яғни, n =2k (n- натурал caн) болғанда 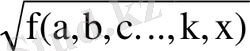-ның тек арифметикалық мәнін ғана қарастырамыз.

Мұндай теңдеулерді шешу әдетте берілген теңдеудің екі жағын да бірдей дәрежеге шығару арқылы біртіндеп иррационал теңдеуді рационал теңдеуге келтіру арқылы шығарылады. Бірақ мұндай жағдайда бөгде түбірлердің пайда болатыны белгілі. Олай болса, шешу оны мұқият тексеру арқылы іске асырылуы тиіс. Иррационал теңдеуді шешудің қандай да бір жалпы тәсілдерін, сонымен қатар оның қарапайым тәсілдерін көрсету мүмкін емес. Осындай теңдеулерді шешудің әртүрлі тәсілдерін олардың артықшылықтарына мән бермей мысалдар арқылы қарастырайық.

1-мысал. Параметр а -ның мәндеріне байланысты теңдеуді шешіңдер

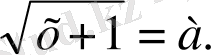
Шешуі: Теңдеу мына жүйеге мәндес

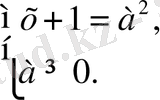
Олай болса, а ≥ 0 болғанда, берілген теңдеудің шешімі х = а ² - 1 болады, ал а < 0 болғанда, шешімі жоқ.

Жауабы: а > 0 болғанда, х = а ² -1; a < 0 болғанда, .

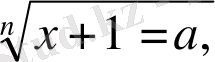
2-мысал. Параметр а -ның мәндеріне байланысты теңдеуді шешіңдер (1)

Шешуі: Айталық n = 2k, k N болсын Онда (1) теңдеу мына жүйеге мәндес:

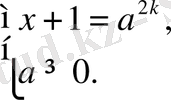
Олай болса, n = 1k, k N, a > 0 болғанда, х = а ^2k - 1, n = 2k, k N, a < 0 болғанда, .

Айталық n = 2k + 1, k N болсын. Онда (1) теңдеу мына теңдеуге мәндес: х +1 = а ^2k+1 х = а ^2k+1 -1.

Жауабы: n = 2k, k N, а >0 болғанда, х = а ^2k+1 -1; n = 2k, k N, a < 0 болғанда, ; n = 2k + 1, k N, а R болғанда, х = а ^2k+1 -1.

3-мысал. Параметр а -ның мәндеріне байланысты теңдеуді шешіңдер:

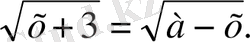
Шешуі: Берілген теңдеу мына жүйеге мәндес:

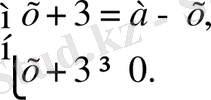
Бұл жүйенің теңдеуінің а ≥ -3 болғанда, х + 3 ≥ 0 теңсіздігін қанағаттандыратын тек бір ғана түбірі 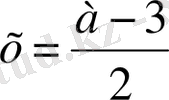бар.

Жауабы: a ≥ -3 болғанда, 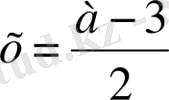; a < -3 болғанда, .

4-мысал. Параметрдің мәндеріне байланысты теңдеуді шешіңдер:

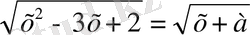(2)

Шешуі: (2) мына теңдеуге мәндес

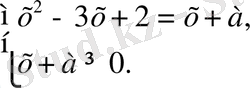
Бұл жүйенің шешімі (3) теңдеудің х ≥ - а теңсіздігін қанағаттандыратын түбірлері бар болғанда және тек сонда ғана шешімге ие болады.

х ² - 4х + 2 - а = 0. (3)

f ( x ) = х ² - 4х + 2 - a. х _T деп у = f ( х ) параболасының төбесінің абциссасын белгілейік.

Мына шарт орындалғанда

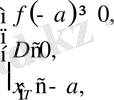
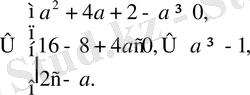
(3) теңдеудің [- а ; + ) аралығында жатқан әртүрлі екі түбірі болады. Олай болса, a ≥ -1 болғанда. (2) теңдеудің түбірлері х = 2 ± 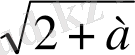болады.

Мына шарт орындалғанда

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс