Анықталған интеграл және Ньютон-Лейбниц формуласы: Риман анықтамасы, есептеу әдістері және геометриялық қолданбалар


Анықталған интеграл. Ньютон Лейбниц формуласы.
- Қисық сызық трапеция ауданын есептеу.
у=f(x) >0 функция [a, b] аралықта үзіліссіз болсын. Сонда жоғарыдан f(x) функция графигімен солдан x=a, оңнан х=в және O х өсімен шекараланған фигура қыйсық сызықты трапеция деп аталады. Бұл трапеция ауданын есептеу үшін алдын [a, b] аралық a=x 0 <x 1 <x 2 < . . . <x n =b нүктелер мен n бөлекке бөлінеді. x i лердің ординаталары мен берілген трапеция n бөлекке бөлінеді. Әрбір бөлектен x i <ζ i <x i+1 шартты қанағаттандырушы ζ i лер алынып f(ζ i ) мәндері табылады. Сонда
n
S n =∑ f(ζ i ) ∆ x i S ке жуықтау тең болып x i нүктелер саны артып
і=1
барған сайын (∆x i =x i+1 -x i кішірейген сайын) S n мәні Sке ұмтылып барады.
- Анықталған интегралдың бар болуы.
Енді бұл мәселені жалпы қарап шығайық [a, b] сегментте үзіліссіз және шенелген y=f(x) берілген болып. [a, b] аралығын n бөлекке бөліп әрбір бөлектен x i <ζ i <x i+1 шартын қанағаттандырушы ζ i лерді алып f(ζ i ) лерді табамыз. Оны
x i+1 -x i =∆ x i лерге көбейтіп. у
n
∑ f(ζ i ) ∆ x i (1) жиындыны табамыз.
I=1
Анықтама. Жиынды (1) max∆ x i->0 да
n 0 а х 1 х 2 х і х і+1 в х
lim ∑ f(ζ i ) ∆ x i шек бар болса оған f(x) функциядан адан в ға
n->∞ i=1
∆x->0
дейін f(x) тан алынған анықталған интеграл делінеді. Ол былай жазылады.
n
lim ∑ f(ζ i ) ∆ x i = ∫ a b [f(x) dx (2)
∆x->0 i=1
n->∞
- Риман интегралы немесе f(x) Риман мағынасында интегралданатын функция деп аталады.
- Анықталған интегралдың қасиеттері.
Анық интеграл төмендегі қасиеттерге ие.
1) ∫ a b cf(x) dx=c∫ a b f(x) dx
2) ∫
a
b
f(x) +
 (x) dx=∫
в
а
[f(x) dx+∫
a
b
(x) dx=∫
в
а
[f(x) dx+∫
a
b
 Equation. 3
(x) dx
Equation. 3
(x) dx
3) ∫ a b f(x) dx=-∫ b a f(x) dx
4) ∫ a b f(x) dx=∫ a c f(x) dx+∫ c b f(x) dx. Бұл теңдік c<a; a<c<b; a<b<c болғанда да орынды.
5) ∫ a b f(x) dx= f(ζ i ) (b-a) (орта мән туралы теорема)
6) [a, b] да minf(x) =m; maxf(x) =М болса m(b-a) < ∫ a b f(x) dx≤М(b-a) болады.
7. кез-келген x
 Equation. 3 [a, b] да f(x) <
Equation. 3 [a, b] да f(x) <
 (x) <
(x) <
 (x) болса ∫
a
b
[f(x) dx<∫
a
b
(x) болса ∫
a
b
[f(x) dx<∫
a
b
 Equation. 3
(x) dx<∫
a
b
Equation. 3
(x) dx<∫
a
b
 Equation. 3
(x) dx
Equation. 3
(x) dx
Ньютон-Лейбниц формуласы.
Берілген [a, b] сгментте f(x) үзіліссіз болып оның осы кесіндідегі алғашқы бейнесі F(U) болсын. Сонда ∫ a b f(x) dx=F(b) -F(a) =F(x) a b (1) болады. Бұл теңдік Ньютон Лейбниц формуласы деп аталады.
Анықталған интегралдың геометриялық мәніне келсек. Егер кел-келген x
 Equation. 3 [a, b] f(x) >0 болса ∫
a
b
f(x) dx жоғарыдан f(x) функция графигі төменнен O
x
өсі солдан x=a оңнан x=b түзу сызықтармен шекараланған қыйсық сызықты трапеция ауданыны тең болады.
Equation. 3 [a, b] f(x) >0 болса ∫
a
b
f(x) dx жоғарыдан f(x) функция графигі төменнен O
x
өсі солдан x=a оңнан x=b түзу сызықтармен шекараланған қыйсық сызықты трапеция ауданыны тең болады.
Ал кез-келген x[a, с] да f(x) >0 кез-келген x[с, b] да f(x) <0 болса онда ∫ a b f(x) dx==∫ a c f(x) dx-∫ c b f(x) dx болады.
1. Анықталған интегралды есептеуде айнымалды ауыстыру
Теорема: y=f(x) [a, b] сегментте ψ(t) [c, b] сегменте үзіліссіз болып a=ψ(c), b=ψ(d) болса.
∫ a b f(x) dx=∫ c d f[φ(t) ] φ ’ (t) dt болады.
а
Мысалы. ∫√a 2 -x 2 dx= x=asint x=0 болғанда asint=0=>t=0
0 dx=acostdt x=a болғанда asint t=п/2
п/2
=∫ 0 √a 2 -a 2 sin 2 t acostdt= =∫ 0 п/2 a 2 cos 2 tdt= a 2 ∫ 0 п/2 (1-cos2t) dt= a 2 t- sin2t п/2 = a 2 п
2 2 2 0 2
2. Анықталған интегралды есептеуде бөлшектеп интегралдау әдісі.
Бірер [a, b] сегментте U(x) =U және V(x) =V функциялары үзіліссіз және дифференциалданушы болсын.
Сонда d(U*V) =VdU+UdV=> UdV=d(U, V) -Vdy
∫ a b UdV=∫ a b dU*V-∫ a b VdU=>∫ a b UdV=UV a b -∫ a b VdU болады.
Мысалы. ∫ 0 п/2 sin n xdx= u=sin n-1 x dv=sinxdx =
du=(n-1) sin n-2 xcosxdx v=cosx
=sin (n-1) xcosx 0 п/2 -(n-1) ∫ 0 п/2 sin n-2 xcos 2 xdx=(n-1) ∫ 0 п/2 sin n-2 x(1-sin 2 x) dx=
=(n-1) ∫ 0 п/2 sin n-2 xdx-(n-1) ∫ 0 п/2 sin n xdx.
∫ 0 п/2 sin n xdx=(n-1) ∫ 0 п/2 sin n-2 x-(n-1) ∫ 0 п/2 sin n xdx
n∫ 0 п/2 sin n xdx=(n-1) ∫ 0 п/2 sin n-2 xdx; => I n = n-1 I n-2
n
n=2k+1 болса I 1 =∫ 0 п/2 sinxdx=1;
n=2k болса I 2 =∫ 0 п/2 dx= п
2
f(-x) =f(x) ∫ -a a f(x) dx=2∫ 0 a f(x) dx
- Анықталған интегралды есептеуде жиі қолданылатын теңдіктер. Егерде f(-x) =f(x) болса ∫-aaf(x) dx=2∫-aaf(x) dx болады.
Мысалы. 2
∫ -п/2 п/2 cosxdx=2∫ 0 п/2 cosx dx; ∫ -5 5 x 2 dx=2∫ 0 5 x 2 dx
Егерде f(-x) =-f(x) болса ∫ -a a f(x) dx=0 болады.
Мысалы: ∫ -a a xdx=0 ∫ 0 п/2 sinxdx=0
3) Егерде f(x+2l) =f(x) болса
∫ 0 2l f(x) dx=∫ a 2l+a f(x) dx болады.
∫ 0 2п sin5xdx=∫ 2п 4п sin5xdx=∫ 4п 6п sin5xdx =0
Анықталған интеграл көмегімен кейбір геометрия есептерін шешу.
1. Жазық фигураның ауданы.
1
0
.
Жазық тiкбұрышты декарттық координаталар системасында ордината осi тiк жоғары қарай бағытталған болсын. Абсцисса осiнен жоғары орналасқан қисықсызықты трапецияның ауданы (3. 3) формуласымен анықталады. Егер интегралданушы функция
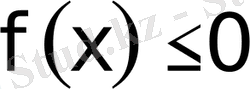
 болса, онда “табаны”
болса, онда “табаны”
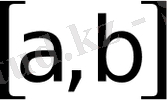 болатын қисықсызықты трапецияны
болатын қисықсызықты трапецияны
 қисығы төменнен шектейдi. Аудан
қисығы төменнен шектейдi. Аудан
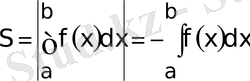 . (5. 1)
. (5. 1)
Интегралданушы функцияның таңбасы
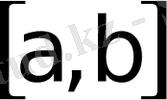 -да өзгермелi болса, онда кесіндiнi функцияның таңбасы тұрақты болатын бөлiктерге бөлемiз. Әрбiр бөлiкке сай аудан (3. 3) не (5. 1) формуласының көмегiмен анықталады. Олардың қосындысы бүкiл фигураның ауданын бередi.
-да өзгермелi болса, онда кесіндiнi функцияның таңбасы тұрақты болатын бөлiктерге бөлемiз. Әрбiр бөлiкке сай аудан (3. 3) не (5. 1) формуласының көмегiмен анықталады. Олардың қосындысы бүкiл фигураның ауданын бередi.
Кесiндiде үзiксiз
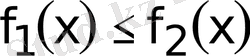
 функцияларын қарастыралық. Түзулермен:
функцияларын қарастыралық. Түзулермен:
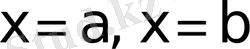 және
және
 қисықтарымен шектелген фигураның (5-сурет) ауданы қисықтардың абсцисса осiне қарағанда қалай орналасқанына байланыссыз табандары
қисықтарымен шектелген фигураның (5-сурет) ауданы қисықтардың абсцисса осiне қарағанда қалай орналасқанына байланыссыз табандары
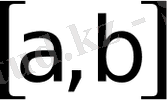 ортақ қисықсызықты трапециялардың аудандарының “айырымы”
ортақ қисықсызықты трапециялардың аудандарының “айырымы”
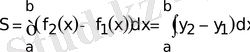 (5. 2)
(5. 2)
ретiнде анықталады.

5- сурет
Кейде қолданысқа айнымаларды рольдерiмен алмастыру арқылы алынған
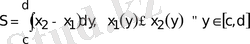 (5. 3)
(5. 3)
формуласы қолайлырақ.
4-есеп:
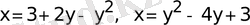 функцияларының графиктерiмен шектелген фигураның ауданын табыңыз.
функцияларының графиктерiмен шектелген фигураның ауданын табыңыз.
Шешу:
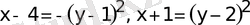 төбелерi сәйкес (4; 1) және (-1; 2) нүктелерi болатын, бұтақтары тиiсiнше солға және оңға бағытталған параболалардың (6-сурет) теңдеулерi. Оларды система ретiнде шешсек, параболалардың қиылысу нүктелерiн: (3; 0) және (0; 3) табамыз. Демек, (5. 3) -те:
төбелерi сәйкес (4; 1) және (-1; 2) нүктелерi болатын, бұтақтары тиiсiнше солға және оңға бағытталған параболалардың (6-сурет) теңдеулерi. Оларды система ретiнде шешсек, параболалардың қиылысу нүктелерiн: (3; 0) және (0; 3) табамыз. Демек, (5. 3) -те:
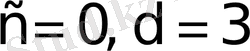 . Параболалармен шектелген аудан:
. Параболалармен шектелген аудан:
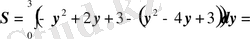
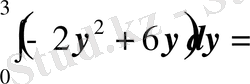
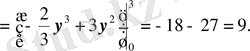
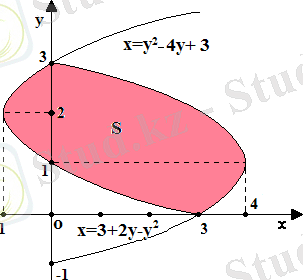
6-сурет
Анықталған интегралды қолданудың екi жүйесi (жолы) бар. Оның бiрi инетгралдың геометриялық мағынасын айқындауда (3-дәрістегі 1. ) баяндалған: табылуға тиiс шама интегралдық қосынды түрiнде жуықтап анықталады. Одан кейiн
 - да шекке көшiп, шаманың дәл мәнiн табамыз. Бiрқатар зерттеулерде басқа жолды ұстану: iзделiнiп отырған шаманың элементiн (дифференциалын-өсiмшесiн) жуықтап тауып, одан берiлген аралықта анықталған интеграл алу тиiмдiрек.
- да шекке көшiп, шаманың дәл мәнiн табамыз. Бiрқатар зерттеулерде басқа жолды ұстану: iзделiнiп отырған шаманың элементiн (дифференциалын-өсiмшесiн) жуықтап тауып, одан берiлген аралықта анықталған интеграл алу тиiмдiрек.
2
0
.
Бiр центрден шыққан сәулелермен және оларды қиып өтетiн сызықпен шектелгн жазық фигура қисықсызықты сектор деп аталады;
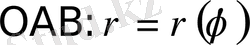 ,
,
 (7-сурет) қисықсызықты секторының ауданын
(7-сурет) қисықсызықты секторының ауданын
 табу керек делiк. Полярлық бұрыштың
табу керек делiк. Полярлық бұрыштың
 элементiне сай келетiн
элементiне сай келетiн
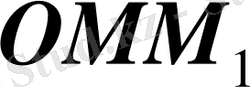 элементар қисықсызықты секторын бөлiп алайық. Оны жуықтап табаны
элементар қисықсызықты секторын бөлiп алайық. Оны жуықтап табаны
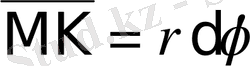 , биiктiгi
, биiктiгi
 түзусызықты үшбұрыш деп қарауға болады.
түзусызықты үшбұрыш деп қарауға болады.
Сонда фигура ауданының элементi
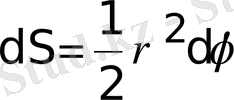 .
.
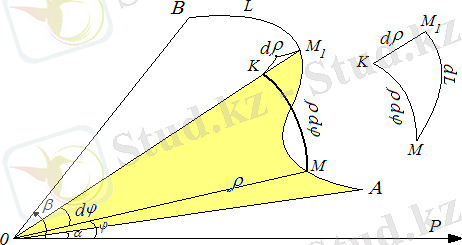
7-сурет
Бұдан
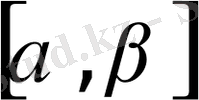 кесiндiсi бойынша анықталған интеграл алып, iздеп отырған ауданды табамыз:
кесiндiсi бойынша анықталған интеграл алып, iздеп отырған ауданды табамыз:
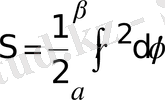 . (5. 4)
. (5. 4)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz