Аралас туындылар туралы теорема, жоғарғы ретті толық дифференциалдар, екі айнымалылы функциялар үшін Тейлор формуласы және экстремумдар


§ 6. 9 Аралас туындылар туралы теорема
Теорема.
Үзіліссіз
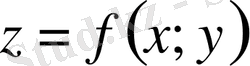 функциясы берілсін және оның үзіліссіз екінші ретті аралас туындылары бар болсын, онда олар өзара тең болады:
функциясы берілсін және оның үзіліссіз екінші ретті аралас туындылары бар болсын, онда олар өзара тең болады:
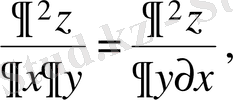 (16)
(16)
Бұл теореманы дәлелдеу өте маңызды, бірақ, өте күрделі. Сондықтан тек дәлелдеу желісін ғана келтіреміз. Мына өрнекті қарастырамыз:
A=[f(x+∆x, y+∆y) -f(x+∆x, y) ] -[f(x, y+∆y) -f(x, y) ] .
Бұл айырмаға екі рет Лагранж теоремасы қолданылады: алдымен х айнымалысы, сонан кейін у айнымалысы бойынша, сонда:
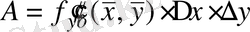 .
.
А өрнегіндегі екінші және үшінші қосылғыштардың орындарын ауыстырамыз да, Лагранж теоремасын тағы да алдымен у бойынша, сонан кейін х бойынша қолданамыз:
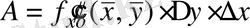 .
.
Шекке көшу арқылы теореманың дұрыстығын дәлелдейміз.
Теореманы жалпылаймыз: аралас туындылардың мәндері біртіндеп дифференциалдау ретіне тәуелді болмайды:
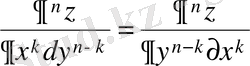 . (16′)
. (16′)
Алдыңғы қарастырылған 1, 2-мысалдарда аралас туындылардың тең болатынын көруге болады:
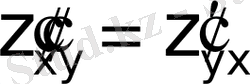 ;
;
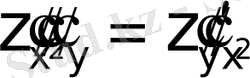 ;
;
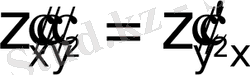
§ 6. 10 Жоғарғы ретті дифференциалдар.
Екі айнымалылы функцияның толық дифференциалын қарастырамыз:
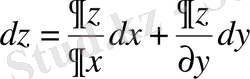 .
.
Анықтама. Бірінші ретті дифференциалдың толық дифференциалы екінші ретті дифференциал деп аталады:
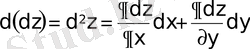 .
.
Толық дифференциалдың формуласын пайдаланып және функция-лардың көбейтіндісі деп дифференциалдаймыз:
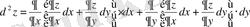 ,
,
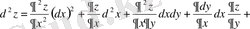
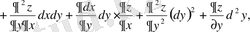
сонымен,
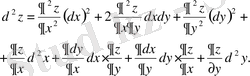 (*)
(*)
Егер х, у тәуелсіз айнымалылар болса, онда (*) өрнегіндегі соңғы төрт мүше нөлге айналады, өйткені dx пен dy - тен алынған туындылар мен дифференциалдар нөлге тең.
Бірақ, егер z күрделі функция болса, яғни х , у- тер басқа тәуелсіз айнымалыларға тәуелді, онда екінші ретті дифференциал үшін (*) формуласы қолданылады.
Біз келешекте екі айнымалылы функцияны ғана қарастырамыз, мұндағы х, у- тәуелсіз айнымалылар. Сондықтан, екінші ретті дифференциал мына түрде беріледі:
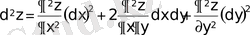 .
.
Үшінші ретті дифференциалын табамыз:
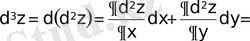
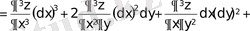
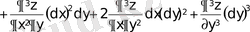 ;
;
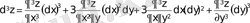 .
.
Үшінші ретті дифференциалды мына түрде берейік:
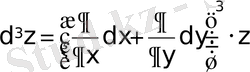 .
.
Жақшаны ашқандағы дәреже туындының ретін көрсетеді, ал әртүрлі дәрежелердің көбейтіндісі функцияның реті әртүрлі аралас туындыларды көрсетеді деп алу керек. Екі тәуелсіз айнымалылы функцияның жоғарғы ретті дифференциалы биномды еске түсіреді. Сонымен, алдыңғы айтқанымыздай:
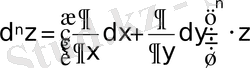 (17)
(17)
Мысал үшін, n=4 болғанда Ньютон биномы бойынша ашып, төртінші ретті дифференциалды аламыз:
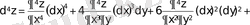
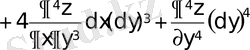 .
.
Мысал. Екінші ретті дифференциалды табу керек.
z=e xy , z′ x =ye xy , z′′ xx =y 2 e xy , z′′ xy =(xу+1) e xy ,
z′ y =xe xy , z′′ yy =x 2 e xy , z′′ yx =(yх+1) e xy ,
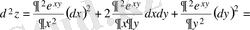
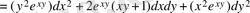 .
.
§ 6. 11 Екі айнымалылы функция үшін Тейлор формуласы.
D
облысында үзіліссіз және кез келген үзіліссіз аралас туындылары бар екі айнымалылы
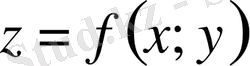 функциясы берілсін.
D
облысының
функциясы берілсін.
D
облысының
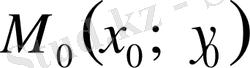 берілсін.
берілсін.
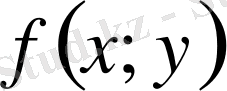 функциясын
функциясын
 және
және
 -ң дәрежелері бойынша жіктеу керек.
-ң дәрежелері бойынша жіктеу керек.
Шешуі.
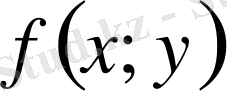 функциясын,
х-
ті тұрақты деп есептеп, бір
у
айнымалысының функциясы деп аламызда оны Тейлор формуласы бойынша жіктейміз.
функциясын,
х-
ті тұрақты деп есептеп, бір
у
айнымалысының функциясы деп аламызда оны Тейлор формуласы бойынша жіктейміз.
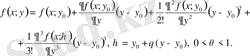 (*)
(*)
Әрі қарай
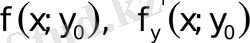 ,
,
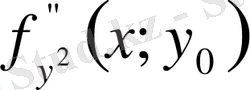 функцияларын аргумент
функцияларын аргумент
 -тің функциялары деп Тейлор формуласы бойынша жіктейміз.
-тің функциялары деп Тейлор формуласы бойынша жіктейміз.
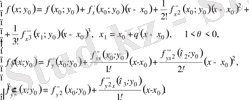 (**)
(**)
(**) қатысты (*) өрнегіне қоямыз:
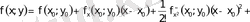
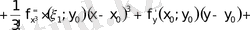
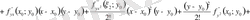
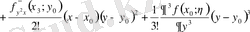 .
.
Функцияны
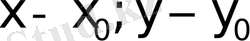 -дің дәрежелерінің өсуіне қарай орналастырамыз:
-дің дәрежелерінің өсуіне қарай орналастырамыз:
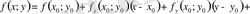
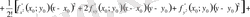
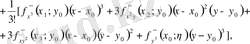
Соңғы тік жақшаның ішіндегі өрнек Тейлор формуласының қалдық мүшесі деп аталады.
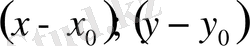 -дерді сәйкес
-дерді сәйкес
 және
және
 деп белгілейік. Сонда екі айнымалының функциясы үшін
деп белгілейік. Сонда екі айнымалының функциясы үшін
 болғандағы Тейлор формуласының түрі былай болады:
болғандағы Тейлор формуласының түрі былай болады:
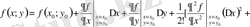
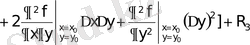 .
.
Бұл өрнекте бірінші және екінші ретті толық дифференциал беріліп тұрғанын көреміз (мұнда
dx-
тің орнына ∆
х,
ал
dу-
тің орнына ∆
у
алынған) . Екі айнымалылы функция үшін Тейлор формуласын кез келген
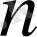 үшін жазуға болады.
үшін жазуға болады.
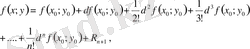 (18)
(18)
мұндағы
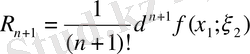 .
.
§ 6. 12 Көп айнымалылы функцияның максимумы және минимумы.
Екі айнымалылы
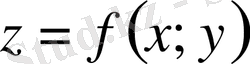 функциясын қарастырамыз.
функциясын қарастырамыз.
Анықтама.
Егер
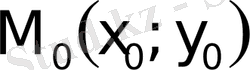 нүктесінің бір кішкентай маңайында
нүктесінің бір кішкентай маңайында
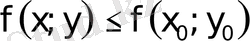
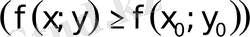 теңсіздігі орындалатын
теңсіздігі орындалатын
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz