Квадрат теңдеулерді шешудің әртүрлі әдістері


Квадрат теңдеулерді шешу жолдарының әр түрлі әдістері
Калиева Г. Б.
8А, №39 мектеп-гимназиясы, Қарағанды қ.
Жетекші: Нұржанова Шолпан Өзбековна
Квадрат теңдеуледі шешу жолдарының әр түрлі әдістері
Калиева Г. Б.
8«А» №39 мектеп-гимназиясы, Қарағанды қ.
Жетекші: Нұржанова Шолпан Өзбековна
Көптеген табиғи процестер мен құбылыстар квадрат теңдеулер арқылы сипатталады, мазмұнды есептердің көбісінің шешуі квадрат теңдеулерді шешуге келіп тіреледі. Квадрат теңдеулерді шешу математикада қарастырылатын тақырыптардың қажетті бірі болып табылады. Квадрат теңдеулерді оның түбірлерінің формуласы бойынша шешу 8-сынып алгебра курсында қарастырылады. Ол арқылы барлық квадрат теңдеулерді шешуге болады. Дегенмен, квадрат теңдеулерді шешудің басқа да әдіс-тәсілдері бар. Осы әдіс-тәсілдерді қарастыру арқылы бұл тақырып туралы терең білуге болады. Кейбір әдістерді тиімді жолдың бірі ретінде есептерді шығару да қолдануға болады. Енді квадрат теңдеулердің шешу тәсілдерін қарастырайық.
1. Теңдеулерді «асыра лақтыру» әдісімен шешу
Мысал.
1)
Шешуі: 2 коэффицентін теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде
Виет теоремасы бойынша
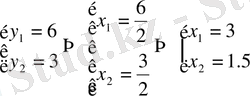
Жауабы:3; 1, 5
2)
Шешуі: «асыра лақтыру» әдісін қолданып, мынаны аламыз,
Виет теоремасы бойынша
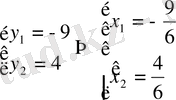 бұдан
бұдан
Жауабы:
2. Квадрат теңдеудің коэффиценттерінің қасиеттері
А.
1) Егер
Дәлелдеуі: Теңдеудің екі жағын да
Виет теоремасы бойынша
a+b+c=0 шартында b= - a-c болады. Олай болса,
2) Егер
Дәлелдеуі: Виет теоремасы бойынша
яғни,
Мысал:
1)
Шешуі:
Жауабы: 1;
2)
Шешуі:
Жауабы:
Б. Егер екінші коэффициент
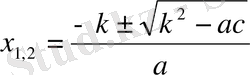
Мысал:
Шешуі:
Жауабы: х 1 =-10, х 2 =4.
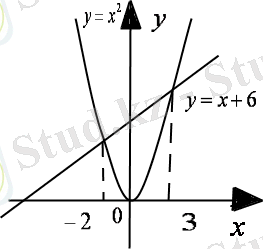
3. Квадрат теңдеуді шешудің графиктік түрі
Бірінші функцияның графигі - координат басынан өтетін парабола, екінші функцияның графигі - түзу (1-сурет) . Енді келесі жағдайлар болуы мүмкін:
-түзу және парабола екі нүктеде қиылысуы мүмкін, қиылысу нүктесінің абциссасы квадрат теңдеудің түбірі болады.
- түзу және парабола жанасуы мүмкін (бір ғана ортақ нүктеде), яғни теңдеудің бір ғана шешімі болады.
-парабола және түзудің ортақ нүктелері жоқ, яғни теңдеудің
түбірі жоқ.
Мысал:
1)
 теңдеуін графиктік тәсілмен шешеміз.
теңдеуін графиктік тәсілмен шешеміз.
Шешуі:
Жауабы:
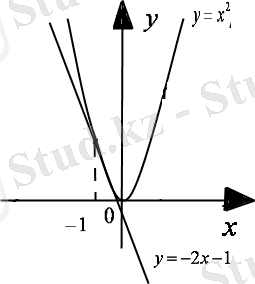
2)
Шешуі:
Жауабы: х=-1
4. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу
y
C(0;
A(0; 1) F
х
ОВ*ОД=ОА*ОС,
B Д(х 2 ; 0)
Бұдан ОС=
Шеңбер центрі АС және ВД хорда ортасында орналаасқан перпендикуляр SF пен SK-ның қиылысу нүктелері болып табылады, сондықтан SK
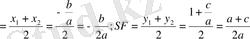
Сонымен,
1)
2) SA радиусты шеңбер жүргіземіз;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz